基于球形收敛和结构一致性的图像修复算法
李志丹,陈 娇,苟慧玲,程吉祥
(西南石油大学 电气信息学院,四川 成都 610500)
数字图像修复概念由Bertalmio等[1]在2000年的SIGGRAPH会议上提出,也被称为图像补全或图像去遮挡。数字图像修复是利用待修复图像内已知信息对未知信息进行估计并恢复补全,达到修复后图像看起来连贯自然的目标。经过近些年的发展,图像修复技术的研究越来越广泛和深入,已成为计算机视觉和图像处理领域的研究热点。
根据修复算法的适用对象,可将现有图像修复算法粗略地分为两类:适合于修复小区域破损图像和适合于修复大区域破损图像。在适合于小区域破损图像修复方面,主要包括基于扩散的方法[1-2]和基于稀疏表示[3-4]的方法。基于扩散的方法是根据合适的偏微分方程对丢失区域进行建模,然后将已知信息根据所建模型扩散到丢失区域。这类方法易引入平滑效应,不能较好地保持修复后图像结构纹理信息的清晰性。基于稀疏表示的修复算法是假定待修复图像的已知信息和未知信息在某个基上具有相同的稀疏表示,通过迭代优化能量方程以重构丢失信息。这类方法仅可较好地修复文字划痕等小区域破损类型的图像,而对包含复杂信息的图像易产生平滑现象。在适合于修复大面积破损图像方面,主要包括基于样本块的修复算法[5]和基于深度学习的方法[6-7]。基于深度学习的方法利用神经网络训练已有数据,根据训练模型生成缺失部分。这类方法训练时间长,且极大地依赖于数据集的选择。
Criminisi等[5]提出的样本块修复算法主要包括两个部分,一是根据优先权法则确定当前待填充块,另一是选择匹配块及填充方式。为提高修复效果,学者们对这两个方面进行了研究并提出大量改进算法[8-18]。如Hesabi等[8]引入梯度和散度信息以构造匹配准则;文献[9]利用基于多方向特征的结构稀疏度函数构造更鲁棒的优先权法则,同时引入多方向特征以构造合适的匹配准则;文献[10]引入边缘特征以优先填充结构部分,并将加权巴氏距离与欧氏距离融合以寻找匹配块;Kumar等[11]在优先权法则中引入边缘长度项以期获得稳定的填充顺序;Lee等[12]利用拉普拉斯金字塔分离纹理和结构区域,增强了对边缘信息的识别能力;文献[13]采用空间变化策略更新置信度项以获得稳定的填充顺序;Alilou等[14]对目标块利用奇异值分解方法构造填充信息并进行填充,获得了良好的修补结果;Cho等[15]引入水平正则化项和背景项来获得稳定的填充顺序,并综合拉格朗日乘子项和方差信息寻找匹配块;文献[16]在匹配准则中引入结构相似性信息来选择匹配块;Ding等[17]提出高斯加权非局部纹理相似性以获得候选块;文献[18]使用动态建模方法确定填充顺序,以确保纹理和边界的可靠传播。
虽然上述算法在一定程度上提升了样本块修复算法性能,但对于较大区域破损的图像仍不能较好的保持其结构完整性,且易出现错误延伸现象。为提高样本块图像修复性能,本文从填充次序和匹配准则两个方面入手。首先为获得稳定的填充次序,将球形收敛准则和基于斯特林理论的置信度更新准则融合,构造鲁棒的优先权法则,以优先修复图像结构信息,同时适度延伸纹理;其次为选择更优的匹配块进行填充,将结构一致性引入以构造更合适的匹配准则。实验结果表明,本文算法能保持修复后图像的结构连贯性,且有效地减轻了误差累积现象。
1 基于球形收敛和结构一致性的样本块图像修复算法
1.1 基于球形收敛的优先权法则
填充顺序的稳定性是保持修复后图像结构连贯性的前提。在修复过程中,样本块图像修复算法若不能较好区分结构与纹理信息,则易导致纹理信息过度延伸而不能较好保持修复后图像的结构连贯性。为提高修复性能,本节提出基于球形收敛的优先权法则,其主要思想是首先优先修复结构部分,而后按照球形收敛规则逐渐向内填充破损区域,以保证填充顺序的稳定性。优先权法则P(p)描述为
(1)
式中:C(p)和D(p)分别为样本块Ψp的置信度项和数据项,定义同Criminisi算法[5];pi为填充边界∂Ω上的像素点;Ψpi为根据max{dS(Ψp,Ψpi),pi∈∂Ω}确定的下一个待修复块,Ψp为当前待修复块;dS(Ψp,Ψpi)为样本块Ψp和Ψpi的空间距离;δ=max{C(pi),pi∈∂Ω},为填充边界上所有置信度的最大值;t为根据δ设定的阈值;ρ为平衡因子。
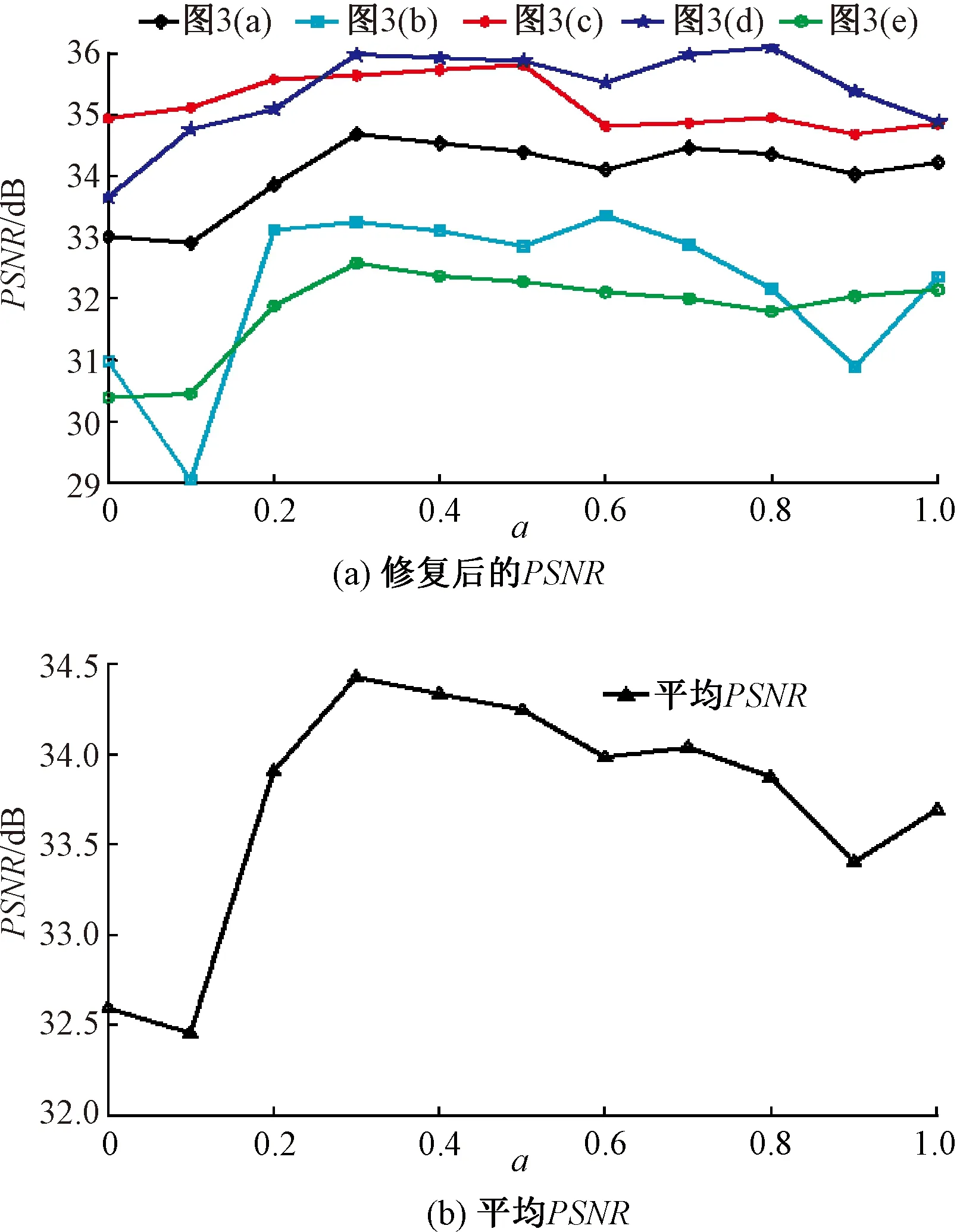
当δ≥t时,因数据项可以反映样本块所处区域特性,故提高数据项的占比ρ,以优先修复图像的结构部分,根据经验分析将ρ取值为0.7;当δ 球形收敛修复过程见图1。Ω为优先修复图像结构部分后剩余的未知区域,假设Ψp′为以p′为中心点的当前待修复块,则下一个待修复块Ψp″将根据max{dS(Ψp′,Ψp″),p″∈∂Ω}确定;Ψp′被填充完毕之后再以Ψp″为当前待修复块,重复上述过程,直至破损区域完全被填充。对于待修复区域有多个时的情形,比如文字或划痕破损,优先修复结构部分后,将剩余的破损区域当作一个整体进行修复。 图1 球形收敛的修复过程 根据置信度的定义[5]可知,随着填充过程的进行,置信度值会迅速衰减并趋近于0。置信度的快速衰减将破坏填充顺序的稳定性,出现结构不连贯现象。 受到斯特林公式的启发,同时为抑制置信度项的迅速衰减,将斯特林公式与指数项eλn结合,提出基于斯特林理论的置信度更新准则为 (2) 式中:C(q)为更新后的置信度值;λ为平衡参数。若λ取值较大,会使更新后的置信度值大于1;若λ取值较小,则衰减速度较快;根据经验本文λ取0.08。 为测试本节提出的基于斯特林理论置信度更新准则的有效性,对图2(a)进行目标移除,掩模图像见图2(b),其修复效果见图2(c)和图2(d)。其中,图2(c)为使用文献[5]算法的修复结果;图2(d)为使用本文置信度更新准则的修复结果;图2(e)为图2(c)和图2(d)中第140行所有像素点的置信度值曲线。 图2 置信度项更新准则对图像修复效果的影响 从图2(e)中可以看出,采用文献[5]算法修复后图像的一些置信度值趋于0,这时将极度削弱优先权法则中数据项的作用,不能很好地优先修复结构部分,出现了图2(c)中结构部分的不连贯。利用本文提出的置信度更新准则修复后图像的置信度值未趋近于0,使得优先权更为稳定,并未出现结构不连贯的现象,见图2(d)。这说明本文提出的基于斯特林理论的更新准则能有效抑制置信度项的衰减速度,保证优先填充结构部分,使得填充次序更为稳定。 由于图像信息的多样性和复杂性,传统样本块修复算法仅采用颜色信息度量样本块间的差异性是不够的,易产生错误匹配,且由于填充过程的贪婪性,从而产生误差累积现象。为减轻误匹配现象,引入样本标准偏差以寻找最佳匹配块。标准偏差用于度量数据集分布的分散程度,是衡量数据值偏离算术平均值的程度。样本块间标准偏差定义为 (3) 基于结构一致性的匹配准则为 d(Ψp,Ψq)=a×dE(Ψp,Ψq)+(1-a)× dstd(Ψp,Ψq) (4) 式中:dE(Ψp,Ψq)为样本块Ψp与Ψq在颜色空间上的欧氏距离;a为权重系数,其作用是平衡欧氏距离和样本标准偏差值。 本文所有实验均采用Matlab2015b和Visual Studio2015作为工具,在Intel Core i5-7500 CPU 3.40 GHz的计算机上进行。实验分为3个部分,分别为参数取值讨论、小区域破损修复及目标移除实验。实验采用的数据为含有丰富结构和纹理信息的图像。因峰值信噪比PSNR值的大小表明了修复后图像与原始真实图像相似程度的高低,故采用PSNR作为客观评价指标以衡量修复效果的优劣。 包含复杂结构和纹理区域的小尺度破损图像见图3。 图3 破损图像 为探讨阈值t及权重系数a对修复性能的影响,选择不同的参数值对图3中各种图像进行修复。 (1)测试t变化时对修复效果的影响。t取不同值时修复后图像PSNR值的变化见图4。从图4(a)中看出,当t开始逐渐增大时,修复后图像的PSNR值几乎没有变化;但当t进一步增大时,PSNR值急剧下降。因t=0.6时平均PSNR最大(如图4(b)中所示),故阈值t取0.6。 图4 不同t值对修复后图像PSNR值的影响 由于t取值较小时PSNR值的变化较小是因小区域破损中结构部分的破损也较少,故选择对破损图像进行填充以验证阈值t选择的合理性。阈值t取不同值时的修复结果对比见图5。从图5可以看出,t=0.6时的修复效果最优,修复后图像的连贯性较好,且没有在填充区域内出现错误填充的情形。 图5 不同阈值t对修复效果的影响 (2)测试a变化时对修复效果的影响。a取不同值时修复后图像的PSNR值变化曲线见图6。由图6(a)可见,不同修复后图像的PSNR值变化趋势并不完全一致,但大致上先是随着a的增大有增大的趋势,而后随着a的继续增大呈下降趋势。因在图6(b)中a=0.3时平均PSNR值最大,故在本文实验中a取0.3。 图6 不同a值对修复结果的影响 为说明本文算法能有效修复划痕等小区域破损图像,选择4幅具有较为丰富结构和纹理信息的图像作为测试对象,见图7(a)。分别用本文算法,以及适合小区域修复的算法[3]、样本块修复算法[5,13]对其破损图像进行修复,见图7(b)。修复结果对比见图7(c)~图7(f),修复后图像的PSNR值见表1。 从图7中可以看出:文献[3]留下了明显的平滑痕迹,且破损区域稍大时出现了结构不连贯现象,如图7(c)中第二行所示;Criminisi算法[5]的修复结果中出现了边缘不连贯现象,如图7(d)中第2行所示,且出现了错误延伸现象,如图7(d)中第1、2、4行所示;文献[13]出现了些微的纹理过度延伸和结构不连贯现象,如图7(e)所示。从图7(f)可以看出,本文算法取得了良好的修复效果,并未出现结构不连贯和误差累积现象。且由表1可知,本文算法均获得了最高的PSNR值,说明本文算法修复效果最优,误匹配现象最低。综上所述,从主观评价和客观评价指标均可说明本文算法的有效性。 图7 小尺度破损修复结果对比 表1 不同修复算法的修复结果对比(PSNR值) dB 选择4幅图像作为目标移除的测试图像见图8(a),其破损模板图像见图8(b),对比样本块修复算法[5,12-13]与本文算法的修复结果见图8(c)~图8(f)。 图8 目标移除结果对比 从图8(c)和图8(e)可以看出,Criminisi算法[5]和文献[13]的修复结果中均出现了结构不连贯现象,以及纹理错误延伸现象,这是由于填充顺序不稳定及匹配准则不合理造成的。文献[12]虽基本上未出现错误填充现象,但其修复结果中也出现了结构不连贯的情形,见图8(d),这是搜索区域有限导致的,未能找到更为合适的匹配块。从图8(f)中可以看出,本文算法较好地保持了结构部分的连贯性和纹理信息连续性,修复效果优于文献[5, 12-13]算法。这是因为本文算法采用的优先权法则和置信度更新准则能获得更稳定的填充顺序,且利用基于结构一致性的匹配准则能获得更合适的匹配块。 本文从填充次序和匹配准则入手以获得良好的图像修复结果,可得出以下结论: (1)通过区分图像位于结构区域或是纹理区域,确定采用结构优先比例计算优先权值或是按照球形收敛法则确定填充顺序,使得填充次序更加稳定。 (2)将斯特林理论引入置信度项更新准则以减缓其衰减速度,进一步提高填充顺序的稳定性。 (3)将结构一致性与颜色信息加权来衡量样本块间的相似性,以获得与邻域一致性更高的匹配块,有效地削弱误匹配现象。 实验结果表明本文算法较对比算法可以获得更高的PSNR值,并且很好地保持了修复后图像结构部分的连贯自然及与邻域信息的连续一致性。但本文算法存在些微的块效应和接缝效应,未来希望基于破损区域特征来确定搜索区域,以进一步提升修复效果。
1.2 基于斯特林理论的置信度更新准则

1.3 基于结构一致性的匹配准则
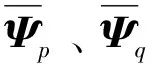
2 实验结果与分析
2.1 参数讨论



2.2 小尺度破损修复


2.3 目标移除

3 结论

