基于SVM分类受电弓振动干扰信号识别
丁宇鸣,刘金朝,徐晓迪,张文轩,杨志鹏
(中国铁道科学研究院集团有限公司 基础设施检测研究所, 北京 100081)
自广深铁路开始,我国在提速干线、高速铁路上开始推广锚段关节式电分相,以满足在列车高速运行时受电弓平稳通过的要求[1]。然而,这种过分相方式在电气上暴露出了新的问题。
某关节式电分相示意见图1。在位置2和位置3之间,接触线与中性线平行悬挂。在该区段,两根导线导高相同,受电弓同时接触2根导线,在一段时间后过渡为仅接触中性线的状态,因此该区段被称为等高区。同样位置4与位置5之间也是等高区。在位置3与位置4之间由于没有任何电气连接,因此被称为无电区。弓头在经过位置2、3、4、5时处于机车惰行状态,经过位置1、6时由于发生电力机车或动车组离网断电和重新进网带电合闸,会产生暂态过程,形成电磁干扰[2]。
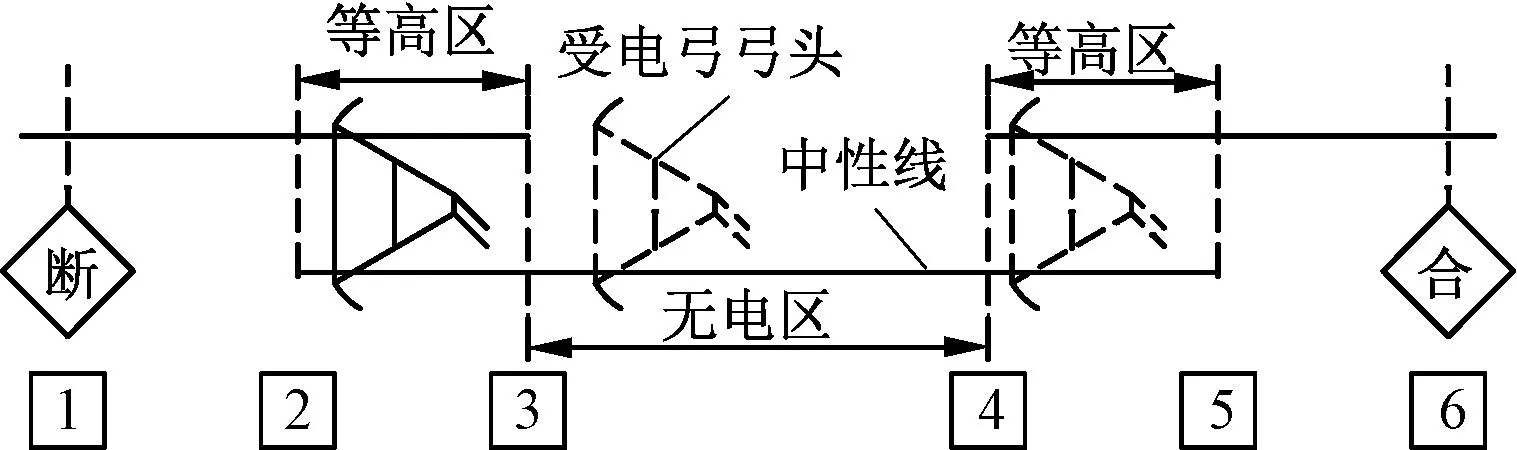
图1 关节式电分相示意图
同时接触网检测车附挂在运营的普速列车尾部,因此用于检测接触网硬点的检测车受电弓在电力机车断开主断路器时,其与电力机车工作受电弓的间距随电力机车与检测车之间的车厢节数的变化而变化。这导致电力机车断开主断路器时的电磁干扰信号位置难以确定。
当这些干扰信号超过了所设的阈值被误判为偏差时,会造成人力物力的浪费,进而导致接触网养护维修的效率降低。因此,对现场环境下受电弓振动信号中干扰信号进行准确、有效识别是非常必要的。
针对电磁暂态过程中的过电压问题,宫衍圣[3]进行了过电压机理分析,对电力机车断电之后惰行通过电分相过程中的各工作状态进行了系统建模,并对不同工作状态转换时出现的暂态过程进行了过电压仿真。文献[4-5]在惰行通过电分相的暂态过程分析基础上,增加了对电力机车离网断电和重新进网带电合闸时的暂态过程分析。苏立轩等[6]对列车离网断电、通过无电区时以及重新进网带电合闸时的暂态过程进行了数学分析和瞬态电磁影响测试。高国强等[7]分析了影响过电压的因素,并提出了限制过电压的措施。
针对断路器开关时产生的电磁干扰。文献[8-9]建立了断路器开关电弧引起的电磁辐射干扰模型,并对辐射场进行了模拟计算。文献[10-11]针对断路器开断过程不同的电流区域提出不同的黑盒模型。
以上这些文献均是针对电学方面,即发生暂态过程时对电路中电压或电流数据进行了分析。然而目前鲜有科研人员对暂态过程中其他传感器受到的电磁干扰进行深入研究。而受电弓弓头的冲击加速度是对接触网进行动态检测的主要检测参数[12]。因此,由电磁干扰所引起的加速度中大量异常数据也会对后续的接触网硬点诊断造成很大影响。
针对干扰信号处理,相关科研人员做了大量研究。袁力等[13]对数据进行信噪分离,运用二值法提取频谱中干扰信号,但是此方法中选用的信噪分离方法对微弱信号的检测能力相对较差。Antonini等[14]提出了一种基于小波包的干扰信号特征提取方法,并对提取的特征进行分类,以识别可能的干扰原因,但该方法在压缩和去噪中的阈值选择规则或分类中的参数或非参数方法的选择等问题仍在研究中,其应用目前是由经验驱动的。Moore等[15]、Mariscotti等[16]分别分析了电磁干扰的频域特性和时频特性,但并未研究如何识别时域上的电磁干扰。Azpúrua等[17]采用经验模态分解(EMD)和瞬态模态分解相结合的方法来分离复杂电磁干扰的主要成分,但经验模态分解(EMD)需要消耗大量时间,因此该方法也不满足工程在线应用的要求。
针对设备运行状态的识别,武立平等[18]提取振动信号多个参数,作为SVM特征量,对若干样本进行了分类。但过多的特征量在处理大量数据时运算复杂度高,不满足工程在线应用的要求。
基于以上分析,本文提出通过计算接触网冲击指数确定偏差位置,再计算各偏差位置的加速度衰减系数,并通过多组已确定是否为电磁干扰的样本作为训练集,加速度最大幅值和加速度衰减系数作为预测变量,基于SVM分类训练出模型,以判断各样本是否为电磁干扰。
1 冲击指数法
由于受电弓垂向加速度具有很强随机性,因此采用接触网冲击指数法将原始数据从高频解调成高稳定性的低频信号,更利于确定接触网硬点缺陷的位置。
接触网冲击指数法详细计算步骤如下:
Step1计算受电弓垂向振动加速度的移动有效值
(1)
式中:Sr为移动有效值的集合,r=1,2,…,N-K+1;K为向前加窗的窗长;xi为滤波后的受电弓垂向振动加速度波形信号的集合,i=1,2,…,N,N为受电弓垂向振动加速度波形信号的个数。
Step2将接触网划分成单元,单元长度一般取为50 m。
Step3计算各单元移动有效值的最大值Smax,记为单元有效值。

Step5计算接触网冲击指数CII为
(2)
Step6超限判断,并记录对应的位置信息[19]。
利用接触网冲击指数法分析某线路。2次通过K862+886附近的受电弓垂向振动加速度波形及对应的接触网冲击指数见图2。图2(a)、图2(b)中为采样频率Fs=5 000 Hz 2次检测的原始数据,对比2张图可以看出受电弓垂向振动加速度信号幅值随机性较大,难以确定评判阈值。使用以能量角度刻画的接触网冲击指数法对两段数据分别进行计算(取K=300)得到图2(c)、图2(d),可以观察到该处出现3个独立的较大峰值,而且波形相似,并且归一化处理后评判指标的分布特性相同。由此表明本文提出的评判方法是稳定的,而且具有很好的重复性。再利用其分布规律自然较容易确定评判阈值。根据对大量测试数据的计算分析,阈值取4.0。

图2 2次通过K862+886附近的受电弓垂向振动加速度波形及对应的接触网冲击指数
2 加速度衰减系数
接触网冲击指数虽然具有良好的重复性,但是当其超限时,难以判断是由客观存在的缺陷引起的还是由干扰信号造成的。
缺陷处、干扰信号处接触网冲击指数见图3。由图3可见,该缺陷处与干扰信号处的接触网冲击指数均远远超出阈值,且数据特征较为相似,因此仅凭接触网冲击指数难以判断偏差是否是由干扰信号导致,还需要分别对2种情况的原始信号数据进行分析。

图3 缺陷处、干扰信号处接触网冲击指数
缺陷处、干扰信号处加速度衰减波形图见图4。由图4(a)可见,当受电弓通过客观存在的缺陷时,原始信号振幅会逐渐减小,经过一段时间,克服外界阻力做功,振动才会衰减到一个正常的较小的范围。而当偏差波形是由电磁干扰引起时,瞬时的电磁干扰导致传感器出现如图4(b)所示瞬时的异常大值,然后瞬间恢复正常。通过现场复核发现,具备这种波形特征的偏差处均不存在硬点缺陷。
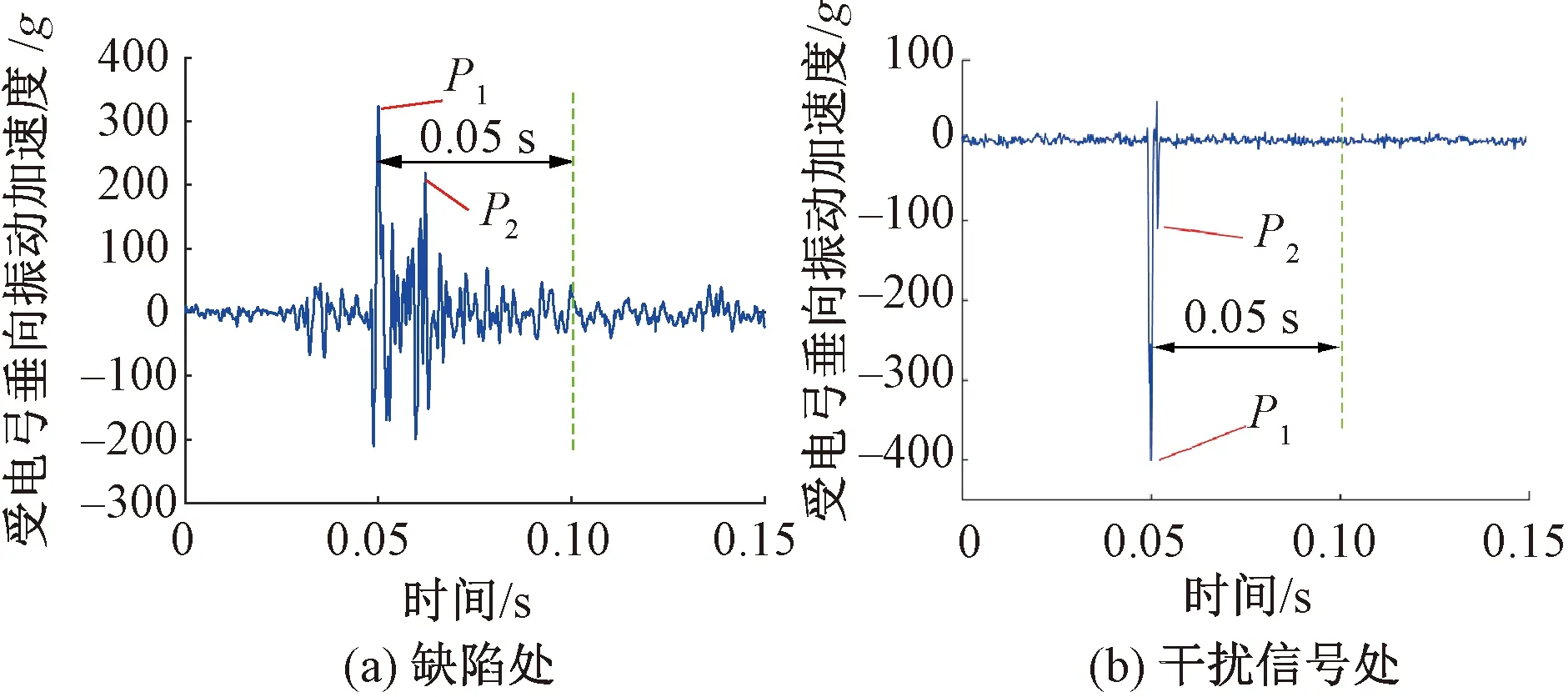
图4 缺陷处、干扰信号处加速度衰减波形图
基于图4这种不同的数据特性,计算偏差位置处受电弓垂向振动加速度的最大幅值P1与加速度数据穿过横坐标后一定时间内的最大幅值P2之比(根据对大量测试数据的计算分析,对该时间范围取为0.05 s),记加速度衰减系数R为
(3)
3 基于SVM分类受电弓振动干扰信号识别方法
3.1 SVM分类的原理
支持向量机(Support Vector Machine, SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面[20-22]。
给定输入数据和学习目标X={X1,…,XN},y={y1,…,yN}(Xi∈Rn;yi∈{-1,+1})若样本线性可分,则支持向量机将分类问题转化为求解凸二次优化问题
(4)
式中:ω为权重;C为惩罚因子;ξ为松弛因子;b为偏置常数。
所得最优分类决策函数为
sign[yi(ω·Xi+b)]
(5)
当多项式核的阶不为1时,可得到非线性SVM。
非线性SVM优化问题为
(6)
所得最优分类决策函数为
sign[yi(ω·φ(Xi)+b)]
(7)
3.2 基于SVM的干扰信号识别
根据对大量测试数据的计算分析,干扰信号的接触网冲击指数往往会远远超出阈值,但也有少数较为严重的缺陷处接触网冲击指数也会远远超出阈值,因此仅凭接触网冲击指数难以判定出偏差是否是由干扰信号导致,而针对不同严重程度的缺陷,其原始信号的加速度衰减系数的分布也有所差异。故将第1节和2节中提出的接触网冲击指数和加速度衰减系数构成信号特征向量,作为SVM分类的输入样本,具体过程见图5。

图5 干扰信号识别流程图
如图5,首先基于受电弓垂向加速度振动信号,提取偏差处最大幅值和受电弓出现最大幅值后0.05 s内最大幅值,将最大幅值与受电弓出现最大幅值后0.05 s内最大幅值之比记为加速度衰减系数,将接触网冲击指数和加速度衰减系数作为振动信号特征向量。提取多组已确定是否为干扰信号的振动信号特征向量分别作为SVM 分类的训练样本和测试样本,训练样本通过经验风险和结构风险最小化原理训练得到特征向量和干扰状态参数之间的决策函数。再应用于测试样本,得到测试样本的分类结果和模型预测的准确率。
4 应用实例
4.1 实验验证与分析
为了验证所提出方法的有效性,采用接触网检测车对多条铁路线路进行检测。接触网硬点测量组件安装于检测列车受电弓弓头滑板的2个支撑点位置。其中加速度传感器的采样频率为5 000 Hz,采样范围为-100g~100g。
基于传感器采集到的受电弓垂向振动加速度,计算各线路的接触网冲击指数,筛选出了其中142处超过管理值的振动信号作为样本,通过人工复核判断每处超限是否为真实的缺陷,如果是真实存在的缺陷,那么记该组样本状态函数值为1,如果现场复核未发现缺陷却在波形中出现一个瞬时大值,即该位置数据存在干扰信号,记其状态函数值为-1。确定好每组状态函数值后,将所有样本分为训练样本和测试样本,其中111组为训练样本,31组为测试样本。


图6 超限处原始波形及对应的接触网冲击指数
对该处超限原始波形进行深入分析,见图7。该处最大幅值P1=96.02g,0.05 s范围内最大幅值P2=82.01g,计算得到加速度衰减系数R=1.17。

图7 超限处加速度衰减波形图
对该处超限进行现场复核,在定位点旁发现严重的导线扭面,这表明该处超限为真实的缺陷。记该组样本状态函数值为1。
将训练样本的接触网冲击指数和加速度衰减系数设为预测变量,将用于判断样本是否为干扰信号的状态函数设为响应。并采用10折交叉验证法,作为对算法准确性的估计。
原始数据集中不同类别的分布,见图8。由图8可见,-1类的数据点分布区域与1类的数据点有所不同。

图8 原始数据集
运用多种SVM分类方法对训练数据进行训练,得到各模型准确率见表1。

表1 多种SVM模型准确率 %
由表1可知,由精细高斯SVM分类方法训练的模型准确度最高,三次和线性SVM其次。
因此,运用精细高斯SVM训练出的模型见图9。采用精细高斯SVM分类方法对训练集进行训练。

图9 运用精细高斯SVM训练的模型
模型的混淆矩阵见图10,图10中4个区域依次为:TN为真负样本;FP为假正样本;FN为假负样本;TP为真正样本。其中左上角和右下角的绿色区域代表样本预测正确,而左下角和右上角区域代表预测错误,由图10可见,仅有6个负样本被误判为正样本。对这些样本进行分析可见:其中4个样本是由于在0.05 s范围内恰好出现了两次幅值相当的电磁干扰,1个样本是由于该电磁干扰幅值较小,冲击指数最大的1个样本则是由于电磁干扰恰好出现在了一个振动幅值较大的病害附近。造成错误预测的情况都较为罕见。
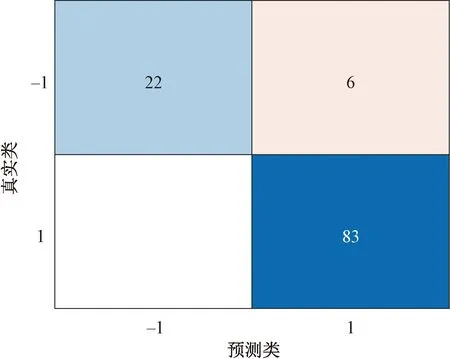
图10 模型的混淆矩阵
由图10混淆矩阵中的TP、FN、FP、TN4个参数值可计算真正率TPR和假正率FPR为
(8)
由TPR和FPR绘制成的ROC曲线见图11,ROC曲线围成面积为AUC,图中显示该模型的AUC=0.94,这表示模型分类效果很好。
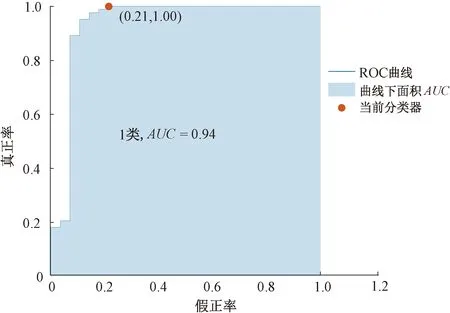
图11 模型的ROC曲线
将模型导出,并将测试样本的预测变量CII、R以及响应导入模型,得到预测的响应,与已知类别的响应进行计算验证,得到准确率为96.77%。
由散点图、混淆矩阵和根据ROC曲线计算出的曲线下面积AUC以及测试样本的准确度,可知该模型在进行判断偏差是否为瞬态电磁干扰的准确率较高。
4.2 对比传统带通滤波干扰信号识别方法
为了验证所提出方法的优势,与传统带通滤波干扰信号识别方法对比。
通过对若干硬点缺陷数据进行时频分析,见图12。能量主要分布在20~800 Hz,对111组训练样本进行带通滤波。

图12 硬点缺陷数据时频图
将训练样本的加速度衰减系数和滤波后计算得到的加速度衰减系数设为预测变量,用于判断样本是否为干扰信号的状态函数设为响应。并采用10折交叉验证法,作为对算法准确性的估计。
运用精细高斯SVM训练出的模型见图13。由图13可见,与本文方法相比,该模型预测错误的数量较多。
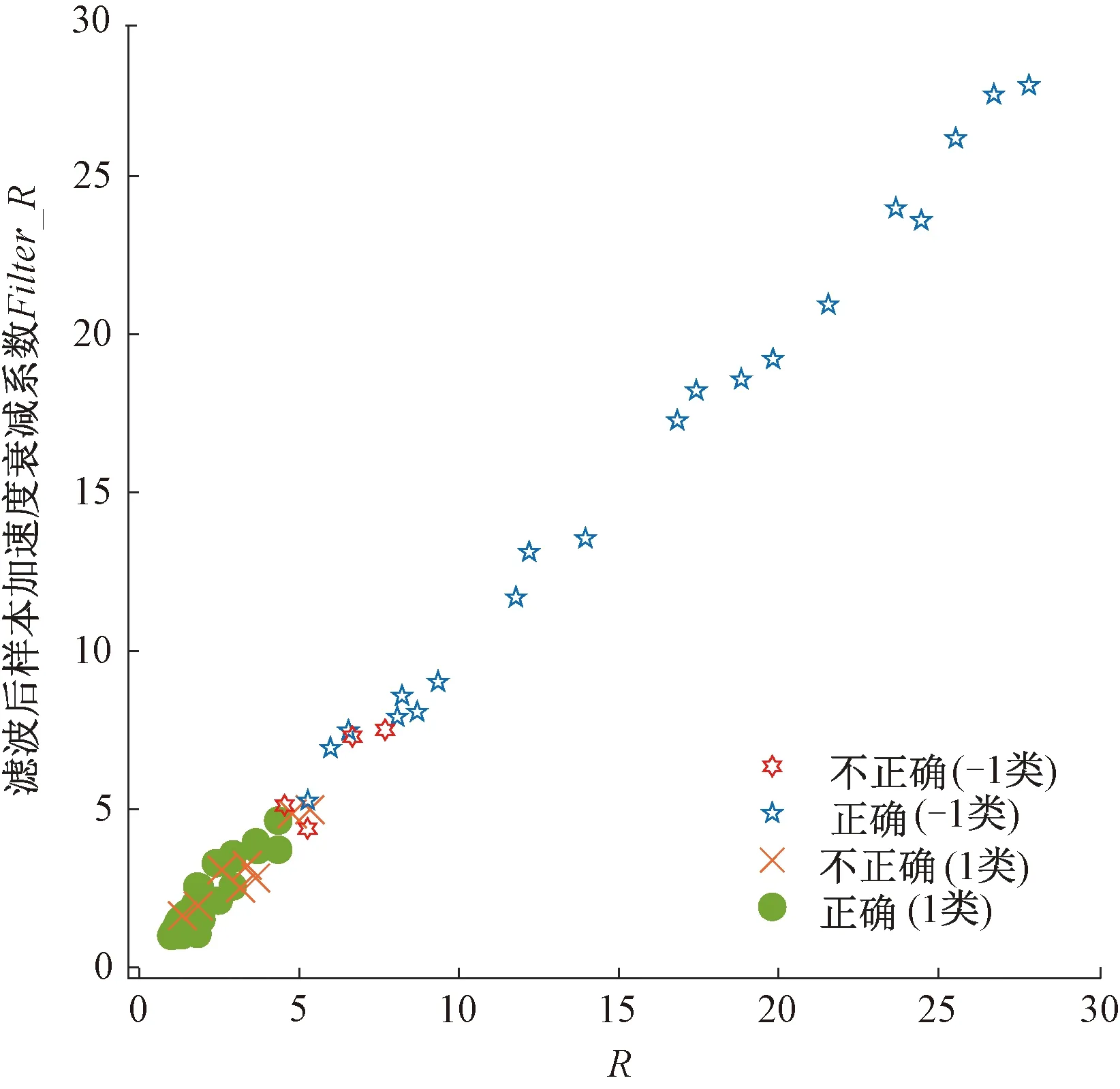
图13 运用精细高斯SVM训练出的模型
该模型的ROC曲线见图14。由图14可见,该模型的AUC=0.90,低于本文提出的方法。

图14 模型的ROC曲线
对若干干扰信号数据进行时频分析,见图15。由图15可见,单个干扰信号的频率范围分布较广,在20~800 Hz范围内存在大量能量。因此仅凭带通滤波无法去除干扰信号,这导致模型预测结果不够精确,见图13,在滤波后干扰信号的加速度衰减系数并没有显著的下降。

图15 干扰信号时频图
仅将加速度衰减系数作为预测变量已能筛选出大部分干扰信号,但针对加速度衰减系数偏小的干扰信号不能做到很好的识别。而本文所提出方法将接触网冲击指数也设为一个预测变量,能够很好反映缺陷引起弓网间冲击的特性。实验证明本文方法识别效果优于传统带通滤波识别方法。
5 结论
本文以识别受电弓振动信号中的干扰信号为目的,提出了基于SVM受电弓振动干扰信号识别方法,通过计算接触网冲击指数确定偏差位置,再计算各偏差位置的加速度衰减系数,将2个指标共同作为预测变量,训练多组已知是否为电磁干扰的样本,得到SVM分类模型。通过算例分析、多个指标的评判、以及测试集的验证,结果表明该方法AUC达到0.94,对比传统的带通滤波干扰信号识别方法效果更佳,能很好的判断偏差是否为瞬态电磁干扰,更好地指导接触网养护维修,满足工程在线应用的要求。

