移动闭塞条件下重载铁路列车流特性研究
董世鑫,谭立刚,魏玉光
(1.北京交通大学 交通运输学院, 北京 100044;2.中国国家铁路集团有限公司 科技与信息化部, 北京 100844)
我国铁路煤炭运输通道广泛采用重载铁路技术,大秦铁路通过构建集疏运一体化系统,采用合理的列车速度、密度及重量匹配技术,已常态化实现4.5亿t年运量,成为我国重载铁路技术的典型代表。在现有固定自动闭塞制式下,大秦铁路线路能力已得到充分利用,为进一步提升重载铁路运输能力,有必要研究适应重载运输的新技术。美国学者Harold最早于1915年提出移动闭塞的设想与实现原理,我国学者汪希时于1963年在国内首次提出“移动闭塞”的概念[1],此后得到广泛关注与研究。随着通信与控制技术的快速发展,移动闭塞技术在国内外城市轨道交通系统中广泛运用。国外城市轨道交通的移动闭塞列控系统发展较早且较为成熟,我国城市轨道交通早期研究相对滞后,直至2010年,自主研发的CBTC系统在北京地铁亦庄线开通运营,并逐步推广至全国。
我国铁路采用多种信号制式,高速铁路多采用准移动闭塞制式的C2、C3级列控系统,普速铁路和重载铁路多采用三显示、四显示自动闭塞,目前仅朔黄铁路正在开展移动闭塞信号设备改造,我国铁路移动闭塞技术仍处于起步阶段。欧洲的ETCS-3、美国的PTC以及我国的CTCS-4列控系统均为移动闭塞制式,但尚未得到广泛运用,仅瑞典采用ETCS-3在低速低密度的线路投入商业使用。
大秦重载铁路运输组织与城市轨道交通有较多相似之处,如固定编组、固定列车载重以及相对简单封闭的线路条件,相对简单的行车模式为移动闭塞技术的率先应用创造了有利条件[2]。移动闭塞系统能有效提升线路运输能力,是重载铁路未来发展的关键技术。
研究移动闭塞条件下重载列车流的流量、密度和速度关系是分析重载运输效能的理论基础。基于列车运行控制机理的探讨[3-5],国内外学者结合元胞自动机模型,建立列车追踪运行仿真模型,并分析列车流特性[6-9]。同时,移动闭塞条件下的列车追踪运行过程类似于道路车辆跟驰,部分学者将跟驰模型用于列车追踪运行仿真[10-11]。在宏观层面上,Corman[12]认为描述交通流Q-K-V关系的宏观基本图(Macroscopic Fundamental Diagram,MFD)可作为交通控制中的监视工具,实时了解交通状况并确定相应控制措施,从而缓解拥塞。
既有研究多集中于列车微观跟驰状态,少量从宏观层面对列车流状态进行描述与研究,但均未具体描述列车流状态变化起因及过程,仅以晚点时间或能力变化的形式分析列车流状态变化的结果,缺乏对列车流的直观认识。
本文首先在以往研究的基础上,建立描述流量与列车速密重关系的铁路MFD,用以分析重载列车流的特性及运行现象。之后基于优化速度(Optimal Velocity,OV)模型,建立移动闭塞条件下列车追踪模型,以大秦铁路为背景进行仿真模拟,根据模拟结果绘制仿真重载列车流Q-K-V关系图,并与理论基本图进行对比分析,证明仿真模型的可靠性,解释铁路列车流与道路交通流的异同点。在此基础上,分析线路通过能力与列车速度、列车长度、线路限速及坡度、以及采用ECP优化制动性能的关系。最后将列车微观追踪状态与MFD相结合,进一步研究移动闭塞条件下重载列车流冲击波产生的机理及传播规律,为重载铁路列车流的管控提供理论基础。
1 移动闭塞条件下列车追踪模型
1.1 OV跟驰模型
为了解决Newell模型在起停车过程中过大加速度的问题,Bando[13]提出OV模型,其本质上与Newell模型具有相同的形式,表达式为
(1)
(2)
式中:k为敏感系数;v(t)为t时刻车辆速度的速度,m/s;Vov(·)为优化速度,m/s;xgap为车辆间距,m;Vmax为车辆最大运行速度,m/s;xc为安全车距,m。
OV模型及其扩展模型能良好地模拟出道路交通流的复杂现象,如时走时停、相变、迟滞等,被广泛应用,但此模型往往会产生不切实际的加速度。
1.2 模型改进要求及假设
基于列车追踪运行特点,针对既有OV模型缺陷进行修正,使其能再现移动闭塞下铁路列车流的微观追踪特性,需满足以下3个条件:
①避免列车出现过高的加减速度,对模型中列车的加减速进行极值标定。
②列车运行过程中,安全追踪距离Dsafe实时变化,与列车运行速度、区段限速及坡度等有关,为保证列车安全高效行驶,不应取常数。
③实际间距xgap和安全追踪距离Dsafe之间的相对关系决定加速度的数值,即加减速度应在一定范围变化。
为便于仿真分析,作以下假设与说明:
①列车运行过程中,通过电阻制动与空气制动匹配可动态调整列车加速度。
②忽略列车在长大下坡道的循环制动过程。
③列车为单质点模型。
1.3 列车OV追踪模型
针对上述要求,建立列车追踪模型为
an(t)=
(3)
xgap=xobj-xn(t)
(4)
式中:an(t)、vn(t)、xn(t)分别为t时刻n列车的加速度、速度、质心位置;xobj为追踪目标点位置;Dsafe为列车以当前速度运行时与追踪目标点的安全追踪距离,m;Vopt(·)为优化速度函数;a+、a-分别为列车最大加速度、最大减速度,m/s2;α为修正系数。
同理,优化速度函数Vopt(·)也需改进为
Vopt(xgap)=
(5)
式中:Dminsafe为列车速度为0时与追踪目标点的安全追踪距离,m;Dmaxsafe为列车以最大限速运行时与追踪目标点的安全追踪距离,m;β为修正系数。
将式(5)中改进的优化速度函数代入式(3),可得
(6)
1.4 模型参数分析
本文中列车追踪模型主要侧重于保证前后列车的安全追踪状态,重点分析移动闭塞系统中列车在区间追踪时的交通流特性,暂不考虑车站到发过程。
(1)区间追踪运行分析
移动闭塞系统中列车区间追踪示意图见图1。

图1 移动闭塞系统中列车区间追踪示意图

移动闭塞条件下,在区间追踪运行时,无论何种状态下,前后列车必须保持安全追踪距离,如图1所示。正常情况下追踪目标点为前车位置xn-1(t),安全追踪距离Dsafe为
Dsafe=Sb+vn(t)·t附+Ls+Ltrain
(7)
式中:t附为追踪附加时间,s。
若前方为限速区段时,追踪目标点改为限速区段分界点xf,安全追踪距离Dsafe为
(8)
列车制动距离Sb由空走距离Sk和有效制动距离Se组成,本文采用等效法[14]计算有效制动距离Se,则列车制动距离Sb为
(9)
式中:v0、vz分别为制动初、末速度,m/s;τ为列车制动空走时间,s;ϑh为列车换算制动率;ρs为距离等效摩擦系数;ωs为距离等效单位基本阻力;ij为加算坡度千分数。式中另外2种安全追踪距离Dmaxsafe和Dminsafe的差异在于制动初速度分别取为0和Vmax。
(2)坡度区段运行参数
由式 (9)可知,列车制动距离与线路坡度密切相关,速度相同时,上坡道区段列车制动距离Sb较短。由于重载列车牵引质量大,当坡度较大时,机车牵引力可能小于运行阻力,列车持续减速,无法保持相对稳定的追踪状态。根据大秦铁路机车牵引特性及列车牵引重量,可确定限制坡度不大于2.5‰,故为得到相对稳定的重载列车流,本文中上坡道区段的坡度应不大于2.5‰,坡道上列车均衡速度则可根据坡度值反推。
在下坡道区段,由于坡道附加阻力存在,列车往往需采取制动工况。当坡度较小时,电制动力可抵消坡道附加阻力,可保持相对稳定的重载列车流,但列车均衡速度低于平坡区段。当坡度较大时,需采取循环制动,导致列车流起伏波动,为便于分析,取最大平均速度作为列车均衡速度,本文依据列车均衡速度分析坡度区段上的重载列车流。
此外,由于坡道附加阻力的变化,列车在坡道区段上所受合力发生变化,则列车最大加减速度也需依据坡度μ进行修正:a-′=a-+μ/108,a+′=a++μ/108。
2 参数初始化
仿真模拟时,以大秦铁路重载列车作为仿真对象,为便于仿真分析,本文选取的重载列车编组形式见表1。

表1 大秦线列车编组形式表
常用制动系数取0.6,安全余量Ls=100 m;追踪附加时间t附=60 s;a+和a-在平坡区段分别取0.1、-0.35 m/s2;α=1.05,β=3;仿真步长为1 s,演化时间T=10 000 s。
为保证初始状态列车互不干扰,系统发车间隔Tint应不小于Tmin,Tmin=Dsafe/Vmax,意味着最小追踪间隔时间与列车类型、线路限速及坡度密切相关。为避免初始随机因素波动影响,选取T=1 000~5 000 s区域内的列车流,计算密度k=1 000·(N-1)/ΔX(t),流量q=k·∑vn(t)/N。
仿真模型采用开放型边界条件, 边界条件定义如下:①线路起点每隔时间Tint新生成一列列车,若起点为车站,初速度为0,否则为线路初始限速Vmax,之后按照更新规则式(6)进行追踪运行;②列车在线路终点自由驶出系统。
3 移动闭塞条件下重载列车流特性分析
3.1 重载列车流理论基本图
移动闭塞条件下,列车追踪运行类似于道路车辆跟驰,列车相互作用敏感且强烈,后车运动状态与列车间距密切相关,表现出连续流的特性,因此可引入铁路MFD,描述移动闭塞条件下重载列车流的特性及运行现象。
理论情况下,假定列车流为饱和稳态,所有列车速度恒定且均匀,前后列车以安全追踪距离Dsafe密集追踪,则移动闭塞条件下重载列车流理论基本图见图2。为对比分析,假定线路坡度μ为0‰,并考虑3种类型重载列车。

图2 移动闭塞系统中重载列车流理论基本图
重载列车流理论基本图以临界密度kc为界分为自由流与拥挤流两部分,理论Q-K关系为
(10)
图2中理论基本图与高速公路交通基本图极为相似,但实际上却存在关键区别。铁路列车流为强可控流,移动闭塞条件下,依据铁路运行规则集中控车,严格限制流量及密度,故理论Q-K曲线可理解为列车流可行状态与不可行状态的分界线;而公路交通流为弱可控流,车辆运行状态多取决于驾驶员判断,故公路交通基本图多为描述交通流的平均状态,并非界定交通流状态可行与否的曲线。此外,道路车辆短,个体对整体交通流的影响十分微弱;而重载铁路列车长度长且制动距离大,个体特性较为突出,宏观分析时应考虑个体影响。
图2中理论Q-K曲线以下为可行区域,此时列车安全追踪且不高于限速运行,列车流状态越贴近理论Q-K曲线,列车速度越高且追踪愈加紧密;理论Q-K曲线以上则为不可行区域。在移动闭塞条件下,实现列车安全高效运行的实质就是通过调度优化与驾驶操纵,尽可能使列车流贴近理论Q-K曲线。
如图2所示,在不考虑限速时,重载列车流存在理论最大流量Qideal,即线路理论最大通过能力,如在平坡区段上,2万t、1.5万t、1万t重载列车流分别在速度约为142、126、103 km/h时取得理论最大流量Qideal。目前大秦铁路列车实际允许速度不大于90 km/h,因此在移动闭塞条件下,提升列车运行速度,不仅可以压缩在途运输时间,还能提高线路能力。
3.2 仿真重载列车流Q-K-V关系分析
设定仿真线路限速Vmax为90 km/h,坡度μ为0 ‰,以3种类型重载列车作为对象,进行仿真模拟,得到移动闭塞条件下仿真重载列车流Q-K-V关系,见图3。

图3 仿真重载列车流关系图
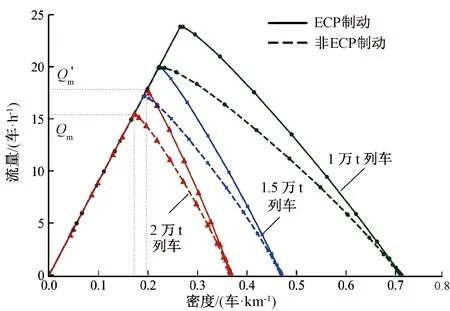
由图3可知,自由流状态下(k 依据仿真结果绘制的重载列车流Q-K曲线与理论基本图在整体上极为相似,但拥挤流部分却略低于理论值,这是由于在模拟列车减速过程中,列车间距会不可避免地大于Dsafe,从而导致密度偏小,由两者的相似性与差异点可证明本文列车追踪模型的可靠性。 考虑不同类型重载列车的载重差异,将流量转化为运量后,得到重载列车流Q-K关系图,见图4,在临界密度kc处,运量取得最大值Volm,即线路输送能力。相同线路条件下,两万吨列车输送能力最大,通过能力最小;而万吨列车通过能力最大,输送能力最小。 图4 仿真重载列车流运量与密度关系 依次改变仿真线路限速Vmax和坡度μ,坡度区段取列车均衡速度作为最大速度,可计算不同线路条件下Tmin与Qm,见表2,步长为1 s,Tmin向上取整。 表2 不同线路条件下的Tmin与Qm对比表 以万吨重载列车作为仿真对象,依据列车追踪模型进行仿真实验,绘制不同限速及不同坡度条件下重载列车流Q-K关系,见图5。 由图5(a)可知,理论Q-K曲线可视为不同限速条件下列车流Q-K关系图的“外包络线”,随着线路限速Vmax降低,最小追踪间隔Tmin增大,最大流量Qm,即线路通过能力逐步降低。由图5(b)可知,在上坡道区段,列车制动距离SZ虽降低,但列车均衡速度也降低,最大流量Qm,即区段通过能力,仍略低于平坡区段。在下坡道区段,当坡度μ增大时,列车制动距离SZ虽增加,但列车均衡速度却降低,最大流量Qm,即区段通过能力随之降低。 图5 仿真重载列车流Q-K关系 在实际运行中,由于牵引制动过程的复杂性,加速度波动剧烈且无法瞬时改变,故列车常低于限速运行,且实际列车间距大于Dsafe,尤其在需循环制动的长大下坡道区段,因此实际列车流状态往往会比仿真列车流Q-K曲线更低。 电控空气(ECP)制动对于列车制动效果有极大的改善[15],在移动闭塞系统条件下,能够充分发挥机车车辆与线路的能力,其主要特点包括: (1)整列车所有车辆同步制动和缓解,使重载列车常用制动距离大大改善,正常速度下制动距离可降低30%到60%。 (2)支持逐步缓解功能,增强重载列车在长大下坡道的可操作性,提高列车平均速度,从而提高通过能力。 按ECP制动可压缩列车制动距离50%计算,取仿真线路限速Vm为90 km/h,坡度μ为0‰,分别以3种类型重载列车作为对象进行仿真,ECP制动条件下仿真重载列车流Q-K关系,见图6。 图6 ECP制动条件下重载列车流Q-K关系图 由图6可知,随着列车制动距离降低,安全追踪距离降低,最大流量Qm,即线路通过能力增大,而随着列车长度Ltrain增加,通过能力的提升比例有所降低,见表3。 表3 ECP制动条件下通过能力对比表 ECP制动的投入使用对移动闭塞条件下重载线路通过能力提升具有显著效果,同时在缓解重载列车纵向冲击力,降低列车车钩断裂、脱轨的风险,以及减少重载列车长大下坡道循环制动次数,提高重载列车速度等方面也具有积极作用。 在道路交通流理论中,交通冲击波(shockwave)常用于描述连续交通流的特性,表示到达能力瓶颈前的自由流状态和拥挤流状态之间时空区域的边界条件[16],其传播速度w=Δq/Δk。当相邻区段的通过能力急剧减小,易产生能力瓶颈,若初始流量需求大于瓶颈能力,则会形成冲击波。 在重载铁路系统中,在长大下坡道或临时限速地段,由于列车减速也会不可避免形成冲击波。尤其在移动闭塞条件下,列车相互作用敏感且强烈,表现出连续流的特性,冲击波效应更为明显。 交通冲击波会扰乱连续的列车流状态,迫使列车在能力瓶颈前减速以较大的列车间距追踪运行,导致列车晚点时间逐步增加,影响列车运行秩序。因此分析重载列车流冲击波的成因与传播规律,对理解并缓和列车拥堵状态和晚点传播有积极意义,为移动闭塞条件下重载列车流的管控提供理论基础。 设定仿真线路全长为50 km,分为3个区段,线路参数见表4,以万吨重载列车作为对象进行仿真。为对比分析,当限速改变时,坡度为0 ‰;当坡度改变时,限速取列车均衡速度。 表4 仿真线路参数 当区段2限速为36 km/h,坡度μ为0 ‰,发车间隔Tint=181 s时,列车时空轨迹图及冲击波分析图如图7所示。列车流初始饱和稳态为图7(b)中A点,当前车减速进入区段2后,前后列车速差导致列车间距迅速缩小,故后车需提前降速以拉大列车间距,且后续列车降速的位置逐步向上游传递,从而形成反向冲击波,传播速度wAB为-26 km/h。区段2内列车流稳态可对应图7(b)中B点,此时车流速度为36 km/h,流量接近于区段2通过能力。 区段3限速恢复为90 km/h,能力瓶颈消失,列车加速进入区段3且互不干扰,密度减小,流量却不变,直至达到区段3内列车流稳态,即图7(b)中C点,此过程(B至C)不产生冲击波,wBC为0。 图7 Tint=181 s,Vm=36 km/h 冲击波传播速度wAB可从侧面描述列车流受影响程度,传播速度越大,列车晚点传播效应越明显,运行秩序愈加混乱。如表5所示,增加发车间隔Tint(降低初始流量需求)或提高区段2限速(提高瓶颈能力),传播速度wAB均会减小,即列车减速的位置向上游移动得较慢,意味着列车晚点时间降低,运行秩序缓解。 表5 进入限速区段冲击波传播速度对比 如表5所示,当区段2限速为36 km/h,发车间隔Tint取241 s,此时流量需求虽等于区段2通过能力,但仍会产生较小冲击波。主要原因是重载列车长度长且制动距离大,即便流量低于瓶颈能力,前车进入限速区段后,列车间距迅速缩小,但安全追踪距离大,故仍有可能对后车运行造成干扰。 在铁路系统中,尤其是重载铁路,交通流冲击波的成因虽与能力瓶颈有关,但由于列车长度影响,个体特性较为突出,与道路交通流冲击波仍有差异,如上所述,还需结合重载列车微观追踪的特殊性具体分析。 当区段2坡度μ为-12‰,发车间隔Tint=181 s时,列车时空轨迹图及冲击波分析图见图8。列车流初始饱和稳态为图8(b)中A点,前车进入区段2后,需制动减速,列车间距迅速缩小,故后行列车需提前减速以拉大安全间距,而后续列车减速位置逐步向上游传播,从而形成反向冲击波,传播速度wAB为-20.0 km/h。减速过程中列车流最拥挤状态为图8(b)中B点,拥挤速度Vjam=51.9 km/h,可理解为列车流最低平均速度。B点之后,列车逐渐加速,直至区段2内稳态,即图8(b)中C点,此时车流速度为均衡速度,流量接近于区段2通过能力。 由于列车加速过程(B至C)难以保持一致,见图8(a),列车加速位置会逐渐向下游传播,产生正向冲击波,传播速度wBC为2.4 km/h。若取3 000~6 000 s内的列车流,计算流量和密度并分析冲击波时,则传播速度wBC仅为0.2 km/h,表示后续列车加速过程趋于相同。 区段3坡度为0‰,能力瓶颈消失,列车加速进入区段3且互不干扰,密度减小,流量却不变,直至列车流达到区段3内稳态即,即图8(b)中D点,此过程(C至D)不产生冲击波,wCD为0。 图8 Tint=181 s,μ=-12‰ 进入上坡道区段,列车制动距离Sb虽降低,但列车被动减速,其本质类似于进入限速区段,仍会产生冲击波。如表6所示,若增加发车间隔Tint(降低流量需求)或改变坡度μ(提高瓶颈能力),反向冲击波传播速度wAB均会减小,列车晚点时间降低,运行秩序干扰缓解。 表6 进入坡度区段反向冲击波传播速度对比表 本文结合宏观基本图与列车微观追踪状态分析冲击波,对列车牵引制动过程作简化处理,但实际中由于循环制动,在长大下坡道区段的列车追踪运行十分复杂,交通冲击波会表现出上下波动的状态。 通过瓶颈区段后,列车速度增加,密度降低,流量不变,因此临时限速或坡度区段的存在会导致线路能力的永久损失,故瓶颈区段能力往往决定整体线路的能力。 除上文的两种冲击波外,重载铁路列车流中还有一些可能产生后向冲击波的场景,如与车站作业相关的列车出发、通过和到达过程,以及设备故障紧急停车,这些场景中极可能发生区段能力突变,而出现流量需求大于能力瓶颈的状况。 在铁路实际运营中为保证列车运行秩序的相对稳定,应尽可能避免冲击波产生或削减其影响,而线路能力瓶颈难以改变,因此只有降低流量需求,即扩大发车间隔,以降低对列车运行过程的干扰。同时,在实际运营中,可在一定程度上利用交通冲击波以提高运输效率,如结合重载车站发车特点,灵活调整发车密度,在车站能力与区间能力间进行转化,实现点线能力协调。 本文比较了铁路列车流与道路交通流的异同,建立了描述Q-K-V关系的铁路宏观基本图,对重载列车流的特性及运行现象进行了分析。通过对比分析重载列车流仿真基本图与理论基本图,证明本列车追踪模型能较好地描述移动闭塞条件下列车区间追踪过程。 在此基础上,研究了列车速度、列车长度、ECP制动、线路限速及坡度与线路能力的关系,得出相关结论如下:①移动闭塞条件下,进一步提高大秦重载列车运行速度,能够提升线路通过及输送能力;②相同线路条件下,增加列车牵引质量(长度),虽线路通过能力变小,但输送能力增大;③随着线路限速降低,线路通过能力逐步降低,坡度增大亦降低线路通过能力;④ECP制动技术对于重载铁路能力提升作用显著,能提高万吨重载列车通过能力19.8%;⑤因限速或坡度造成的能力瓶颈区段,是形成重载列车流冲击波的主要原因,对列车运行秩序和通过能力造成较大影响。 本文比较全面、系统地揭示移动闭塞条件下重载列车流的特性,为重载运输中列车流的管控提供了理论基础。下一步研究将着重两方面:①改进列车追踪模型,考虑重载列车在长大下坡道上的循环制动过程;②运用冲击波产生及削减的机理,将列车区间运行与车站接发车作业过程相结合,以期实现重载列车运输能力和效率的动态提升。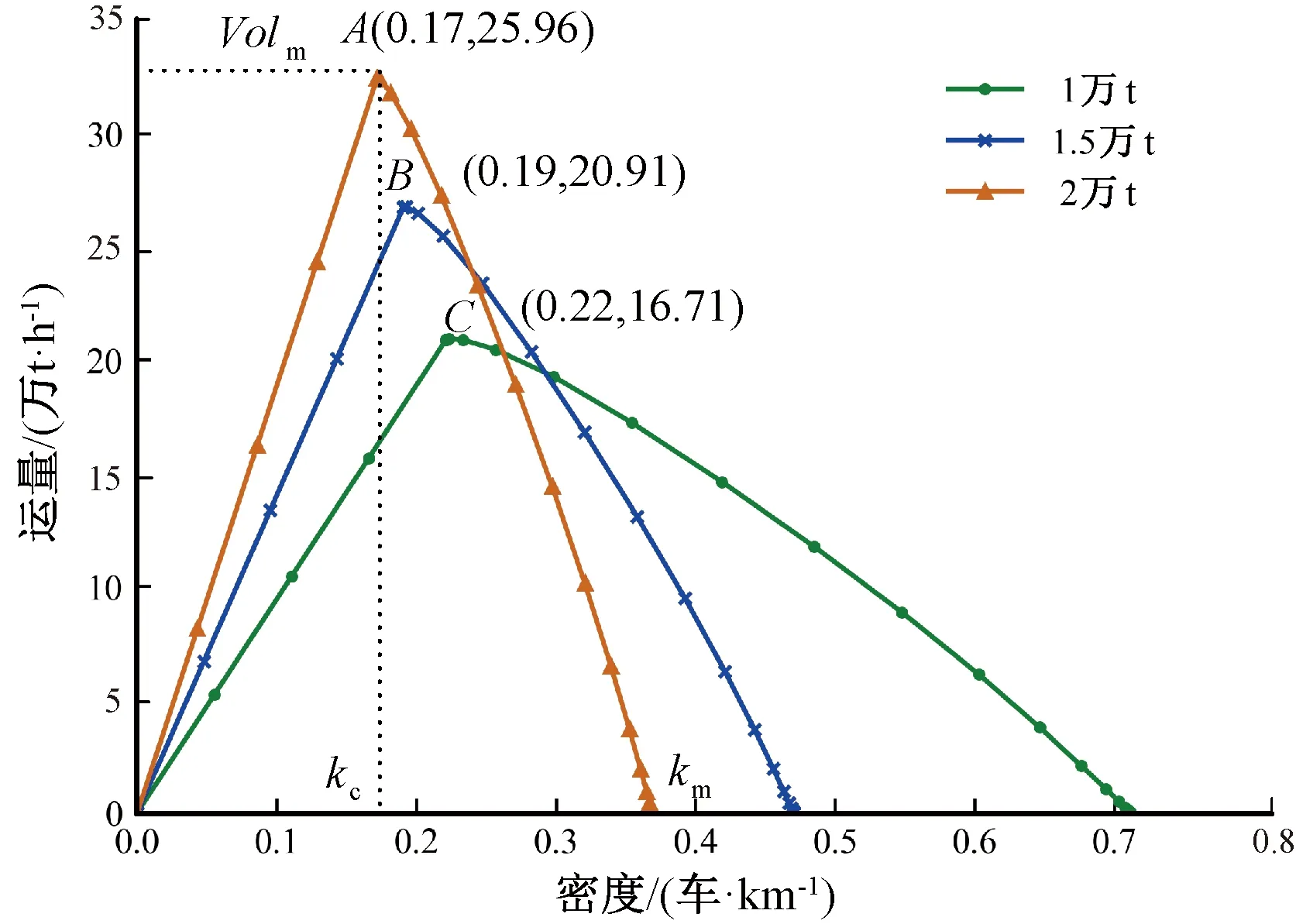
3.3 不同线路条件下仿真重载列车流Q-K关系


3.4 ECP制动条件下重载列车流Q-K关系

4 移动闭塞条件下重载列车流冲击波

4.1 进入限速区段的交通冲击波分析


4.2 进入坡度区段的交通冲击波分析


5 结论

