考虑共因失效的列控车载子系统可靠性分析
张振海,王悦榕,党建武
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.甘肃省人工智能与图形图像处理工程研究中心,甘肃 兰州 730070)
CTCS-3级列控系统是中国列车运行控制系统的重要组成部分,它根据列车的实际运行情况,对列车运行速度、制动方式等进行监督和控制,以保证行车安全和提高行车效率,所以列控系统的可靠性是列车运行安全的重要保证[1]。车载子系统是列控系统的主要子系统,是实现列车速度控制的关键设备,对其进行可靠性评估,有助于改善系统设计和提高维修水平。
列控车载子系统是安全苛求系统,在其配置上多采用冗余方式提高可靠性,故而共同原因失效是不可避免的问题。一旦因同一种原因导致相关冗余元件发生关联失效,不仅会降低系统的可靠性,而且会增加系统失效的发生概率,给行车安全埋下隐患。同时,恢复机制和系统降级运行也同样影响着可靠性评估的结果[1]。
文献[2-3]利用动态故障树分析方法,在分析列控系统和列控中心结构及其功能的基础上,建立故障树模型并进行可靠性分析。文献[4-5]采用Markov模型分别对列控系统和列控中心进行可靠性分析。但故障树分析法和Markov模型存在计算复杂、状态空间爆炸以及对复杂系统计算精度低等问题。文献[6-7]采用β因子模型对系统共因失效进行量化计算。β因子模型简单易计算,但对β因子取值的区间大且分类简单,不利于获得精确的共因失效率。
贝叶斯网络(Bayesian Network, BN)基于概率推理理论,能表达随机变量之间的关系,同时贝叶斯网络对复杂多态系统易表达和推理,且可以通过增加共因失效节点的方式表达共因失效。目前利用贝叶斯网络进行可靠性分析已被应用于各个领域,在铁路信号领域中也有应用[6-8]。另外,文献[9]提出将α因子模型应用在列控安全计算机的共因失效分数计算中,获得更加精确的平均危险侧失效概率。基于此,本文在现有文献研究的基础上,利用贝叶斯网络建立考虑共因失效的列控车载子系统可靠性分析模型,综合考虑恢复机制和降级运行问题,比较β因子模型和α因子模型对共因失效问题进行可靠性量化分析结果的差别,以更好地实现对列控车载子系统的可靠性评估。
1 CTCS-3级列控车载子系统
1.1 系统结构
列控车载子系统是保障行车安全的关键设备,目前在用的CTCS-3级列控车载子系统有CTCS3-300T、CTCS3-300S和CTCS3-300H等型号。其中300T车载子系统采用双系冷备冗余方式,当主系统出现故障时,由司机拨动冗余开关切换至备用系统。300T型车载子系统结构见图1,其中虚框部分为冷备设备。该系统主要包括车载安全计算机、轨道电路信息读取器、GSM-R无线通信单元、列车接口单元、应答器信息接收单元、测速测距单元、人机界面等。

图1 300T型车载子系统结构
列控车载子系统主要功能是实现速度监控、人机交互等。其中,安全计算机承担着核心数据的处理任务,负责从其他模块获取信息、生成速度监控曲线、监控列车运行。安全计算机设置CTCS-2、CTCS-3级控制单元,通常情况下由CTCS-3级控制单元控车,CTCS-2级控制单元处于冷备状态。当CTCS-3级控制单元出现通信故障或无线闭塞中心RBC故障时,又或者在非RBC控制区域运行时,降级至CTCS-2级控制单元控车。无线通信模块和GSM-R电台承担着无线通信信息的传输和处理任务,与RBC共同构建了车-地之间的双向信息传输通道。人机界面完成车载设备和司机的交互功能,司机通过人机界面进行司机号、车次号和模式转换等操作,人机界面向司机提供运行速度、目标速度和警示信息等提示。轨道电路信息读取器和应答器信息接收单元承担着轨旁信号的接收和处理任务,包括轨道电路的低频信息、载频信息和应答器报文等。测速测距单元主要处理速度传感器和雷达信号,实时获得列车速度和距离等信息。列车接口单元是车载子系统和动车组的接口,完成将控制命令输出至动车组并获得反馈信息等功能。司法记录单元完成数据记录功能,记录车载系统的工作模式、司机操作等信息。
1.2 故障树建立
首先,根据故障树的建立方法和步骤[10],在分析系统结构和功能的基础上,选择车载子系统故障为顶事件。其次,由于车载子系统的主要功能是对列车速度进行控制,保证列车在规定的安全速度、距离内运行,所以选择对系统功能影响较大的关键设备作为基本事件,其中人机界面、应答器信息接收单元和应答器天线为双系冷备冗余,其他关键设备采用双机热备冗余。根据事件间信息传递关系以及逻辑关系建立300T型列控车载子系统故障树模型,见图2。图2中各节点及单元名称见表1。

图2 300T型车载子系统故障树模型

表1 节点及单元名称
2 共因失效
共因失效(Common Cause Failure,CCF)是指由于某种共同原因导致两个以上的部件在同一时间或短时内失效。共因失效的存在会提高系统的失效风险,对结构复杂的冗余系统影响很大,所以共因失效对列控车载子系统的影响不可忽视。对存在共因失效的系统进行可靠性研究主要包括两方面,一是可靠性模型构建,二是定量计算共因失效单元的失效率。
2.1 可靠性模型构建
本文采用贝叶斯网络构建可靠性模型,根据贝叶斯网络与故障树之间的对应关系[11],完成故障树向贝叶斯网络转化的图形映射和数值映射。考虑到冗余系统的恢复机制问题,用覆盖参数c反映冗余系统的不完全覆盖程度,即系统从失效状态恢复能力[12]。记事件发生状态为l,事件发生为l=1,事件不发生为l=0;P为概率。热备门和冷备门向贝叶斯网络的转化过程见图3。
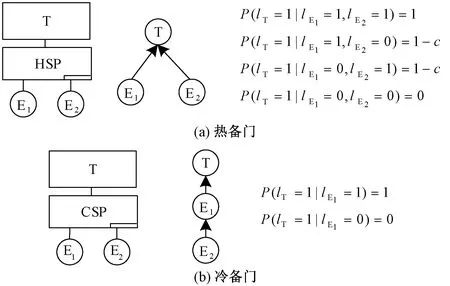
图3 热备门和冷备门向贝叶斯网络的转化过程
考虑共因失效的双机冗余贝叶斯网络模型见图4。其中:单元E1和E2并联构成系统D1;单元E1由独立失效因子E1I和共因失效因子E串联构成;单元E2由独立失效因子E2I和共因失效因子E串联构成。
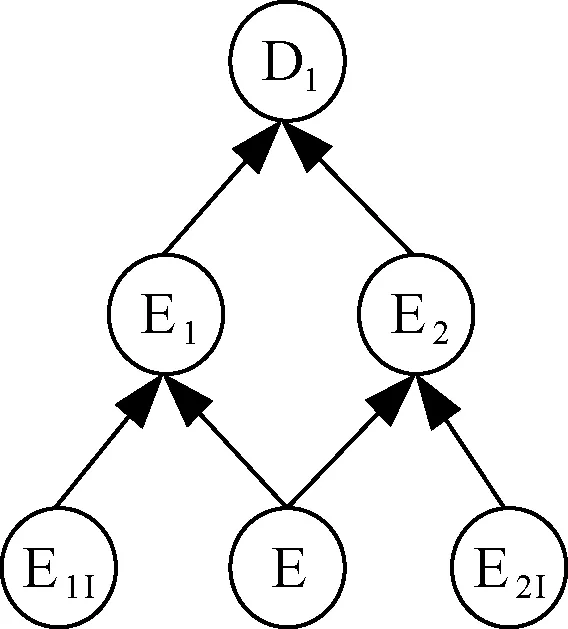
图4 考虑共因失效的贝叶斯网络模型
为保证运营效率,在CTCS-3级线路中出现GSM-R网络或无线闭塞中心RBC设备故障时,车载子系统可在不停车的情况下由CTCS-3级切换到CTCS-2级(以下简称“C3”和“C2”)。由C3级控车模块控车时,C2级控车模块接收轨道电路、应答器和列车速度等信息,但不对外输出。当出现无线超时情况时,触发C3降级到C2逻辑,C2控制模块进入热备状态并周期性地向C3模块发送允许速度,当列车速度降至C2允许速度之下后,系统转入C2级运行。贝叶斯网络能简单清楚地表达多状态系统。针对上述场景,假设C3控制模块有正常、故障和降级状态,分别用lC3=0、lC3=1和lC3=2表示;C2控制模块有正常和故障状态,分别用lC2=0,和lC2=1表示。采用贝叶斯网络构建的可靠性模型见图5。其中,节点T为车载子系统,节点C2为C2控制模块,节点C3为C3控制模块。

图5 采用贝叶斯网络构建的可靠性模型
2.2 共因失效率计算
对共因失效进行量化计算时,由于直接精确统计共因失效事件的发生概率非常困难,所以现有研究通常利用参数模型量化共因失效发生概率。常用的参数模型有α因子模型、β因子模型和多希腊字母模型等[13-15],这些参数值通常从工程经验或现有相关文献中获取。由于多希腊字母模型是β因子模型的扩展,故而本文主要采用α因子模型和β因子模型对系统进行可靠性分析,并加以比较。如图4所示,设节点E1I的失效率为λE1I,节点E的失效率为λE,则节点E1的失效率λE1为
λE1=λE1I+λE
(1)
(1)β因子模型
设某部件总失效率Qt由独立概率QI和相关概率QC组成,β表示相关概率和总失效率的比值,则对于具有独立失效率λI和共因失效率λC的部件,其β因子的计算公式为
(2)
β因子的取值一般在0~0.25之间,但在实际应用中,专家经验给出对于硬件失效,β因子的取值一般在0.1%~10%之间。β因子反映的是部件对环境应力的敏感程度,部件对外部条件越敏感,其β值越高。在对共因失效进行量化时,为了简化计算,认为部件一旦受到共因失效影响,部件会完全失效。
(2)α因子模型

(3)
(4)
式中:αk为k个单元发生共因失效的事件占总失效事件的比例。
在计算共因失效率时,需要确定参数αk的值。设系统中k个单元发生共因失效次数为ak,发生其余类型失效次数为bk,且αk的先验数据服从β分布,即
(5)
(6)
αk的值一般由历次共因失效数据的统计数据而得出,但由于列控系统的共同原因失效数据不足,本文参考文献[9,16]引入共因失效数据,以此作为参考确定αk。
3 考虑共因失效的贝叶斯网络可靠性分析
贝叶斯网络能进行正反向推理,即可以因果推理和诊断推理。当给原因变量提供了证据时,贝叶斯网络能从更新模型中推理出结果变量的概率,同理,当给结果变量提供了证据时,贝叶斯网络能反向推理出原因变量的概率。假设T为顶事件,Ei为底事件和中间事件,各节点间存在条件独立性,则得到联合概率分布为
(7)
式中:n为节点数量;ei∈{0,1}表征Ei事件是否发生。
如图4所示的双机冗余结构,设基本单元寿命服从指数分布,则单元E1和E2的可靠度为
(8)
如果不考虑共因失效,则系统D1的可靠度表达式为
RD1=1-[(1-RE1)(1-RE2)]
(9)
当考虑共因失效时,系统D1的可靠度表达式为
(10)
4 CTCS-3级列控车载子系统可靠性分析
4.1 共因失效组的确定及其故障率的分解
共因失效组的选择直接影响共因失效分析的结果,所以确定共因失效组是共因失效系统可靠性分析的基础。根据共因失效组选择原则,考虑到同一冗余上的部件功能具有相同性或相关性,且其工作环境可能相同,故这些部件常常被选择作为共因失效组。在列控车载子系统中,由于应答器信息接收单元、应答器天线和人机界面为双系冷备冗余,备系在主系无故障时不工作,所以将其视为单系。而其余关键设备采用双系热备冗余,备系在主系无故障时处于工作状态,所以主备系确定为一组共因失效组。
以CTCS-2级控制单元E1、E2为例,E1、E2组成一组共因失效组。首先对其进行失效部件分解,分解成独立失效因子J1、J2和共因失效因子J12,见图6。然后对共因失效组中的失效部件进行故障率分解。设部件独立失效率为λJ1、λJ2,共因失效率为λJ12,由式(1)可得

图6 共因失效部件分解
(11)
(12)
(1) 采用β因子模型对故障率分解
假设列控车载子系统处于最恶劣的环境下,故而取β=10%,各单元寿命为t=2×104h。根据列控车载子系统各单元的可靠性参数和式(2),得到各单元的独立失效率和共因失效率,见表2。

表2 考虑共因失效的各单元失效率 h-1
(2) 采用α因子模型对故障率分解
由于列车运行控制系统缺少共同原因失效的统计数据,本文参考文献[9,16]的无历史数据情况下的αk取值,见表3。

表3 共因参数值
根据表3中的数据,α1取0.974 269,α2取0.025 731,结合某电务段的历史运营数据和文献[4]系统各单元的可靠性参数,带入式(3)计算车载子系统各共因失效组部件的失效率和共因失效率,计算结果见表4。

表4 共因失效部件故障率分解
4.2 系统模型构建
根据列控车载子系统故障树分析模型,综合考虑共因失效、恢复机制等因素,利用MSBNx建立车载子系统贝叶斯网络模型,见图7。

图7 列控车载子系统贝叶斯网络模型
考虑车载子系统存在正常工作和故障两种情况时,车载安全计算机有工作和失效两种状态,分别用0和1表示。其中:状态0表示CTCS-3级列控车载子系统正常运行,即C3控车模块和C2控车模块有一个及以上正常工作;状态1表示CTCS-3级列控车载子系统发生故障,即C3控车模块和C2控车模块均发生故障。假设各单元设备状态相互独立且失效率服从指数分布,取覆盖参数c=0.96,由于篇幅限制,此处省略条件概率表。
考虑因无线闭塞中心RBC或GSM-R通信故障(包括RTU、GSM-R和RSS故障)引起系统降级运行时,车载安全计算机有正常、故障、降级三种状态,分别用0、1、2表示。其中:状态0表示CTCS-3级列控车载子系统正常运行,即C3控车模块正常工作,C2控车模块处于冷备状态;状态1表示CTCS-3级列控车载子系统发生故障,即C3控车模块和C2控车模块均故障;状态2表示CTCS-3级列控车载子系统降级运行,即C3控车模块因通信故障等原因退出控车,C2控车模块正常工作。利用MSBNx建立考虑降级运行下的车载子系统贝叶斯网络模型,见图8。
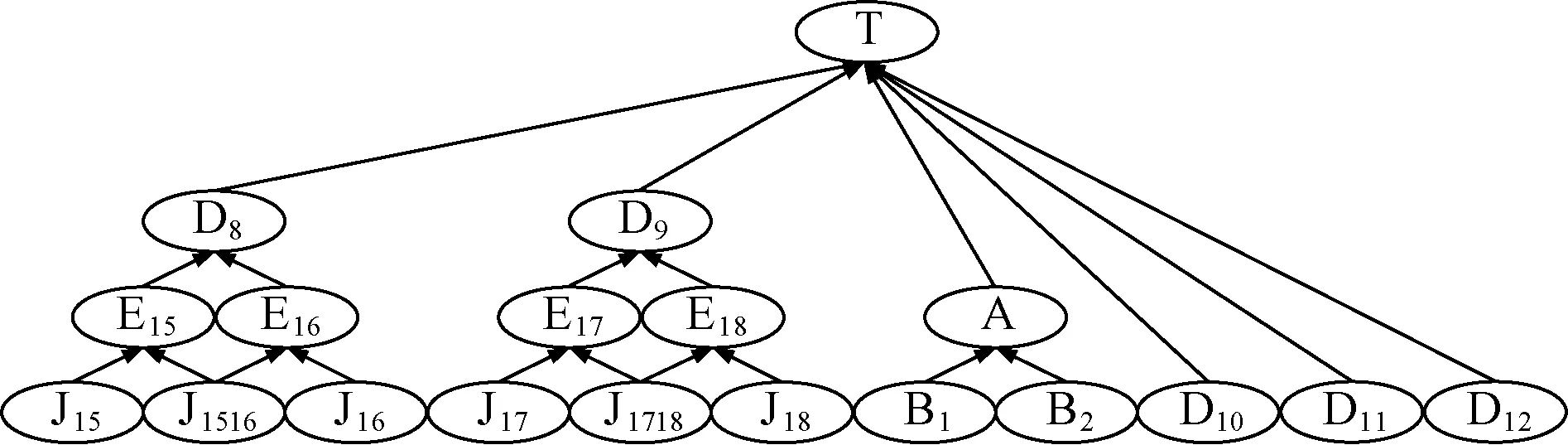
图8 考虑降级场景下的列控车载子系统贝叶斯网络模型
由RBC的失效率为5.00×10-8h-1,RTU的失效率为1.80×10-5h-1,GSM-R的失效率为1.45×10-8h-1,RSS的失效率为1.20×10-5h-1,可得C3处于降级状态的概率为这几个失效率之和,即3.006×10-5h-1。
4.3 系统可靠性分析
根据贝叶斯网络的正向推理,分别得到不考虑和考虑降级运行下的车载子系统各状态概率,见表4。

表4 车载子系统状态概率 %
由表4可以发现,在不考虑系统降级运行的情况下,系统的可用度明显比考虑系统降级运行的可用度高。因而由于故障引起的系统降级运行对车载子系统的可用度影响较大,若要提高系统的可用度,就要减少此类故障的发生。
根据可靠度计算公式式(8)~式(10),取t=2×104h计算出各单元模块的可靠度,见表5。
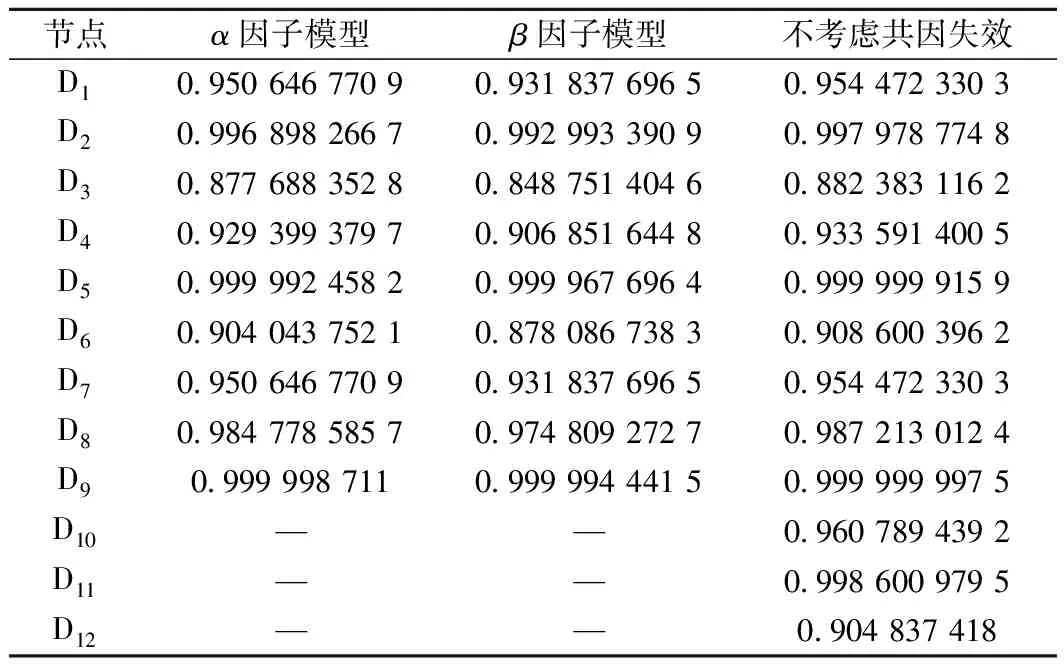
表5 单元可靠度
由表5可以看出,不考虑共因失效时各单元模块的可靠度明显比考虑共因失效的可靠度高。所以双机冗余的设计虽然提高了单元模块的可靠性,但也提高了共因失效发生的概率,若不考虑共因失效因素,会高估可靠性,导致可靠性分析的误差增大。
以C2-CU为例,取t=5×104h,得到C2-CU三种情况下的可靠度对比,以及两种参数模型计算可靠度与不考虑共因失效的可靠度差值,见图9。
由图9(a)可以看出,随着运行时间的增加,C2-CU模块的可靠度逐渐下降,且共因失效对模块的可靠度有一定的影响。由图9(b)可以看出,利用β因子模型计算得到的可靠度与不考虑共因失效可靠的差值比利用α因子模型计算得到的可靠度与不考虑共因失效可靠的差值大得多,原因是取的β值是其范围的最大值,考虑的是系统处于最恶劣条件下的情况,但直接取值划分过于简单,导致计算得到的可靠度较低。相比之下,α因子模型计算得到的可靠度更加贴合实际情况,并且由于本文利用的是无历史数据下的通用取值,待设备单元的共因失效数据越来越完善,利用α因子模型的计算结果将会越来越接近实际情况。
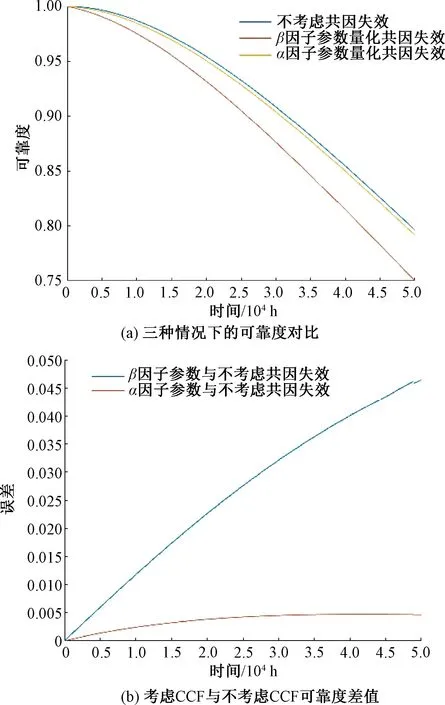
图9 C2-CU可靠度分析
将车载子系统节点T的失效率设置为1,根据贝叶斯网络反向推理,可得系统故障时各单元的失效概率,见表6。
由表6各单元的后验概率可以看出,节点D12、D3、D10、D8、D11的失效率较大,根据失效率从高到低的排序,对这几个单元模块的关注度为DMI>TIU>BTM>PROFIBUS>BTM Ant。可以发现双系冷备的几个模块失效率较大,并且TIU作为CTCS-2级和CTCS-3级列车控制单元的共用模块,其可靠度需要在日常维护时重点关注。
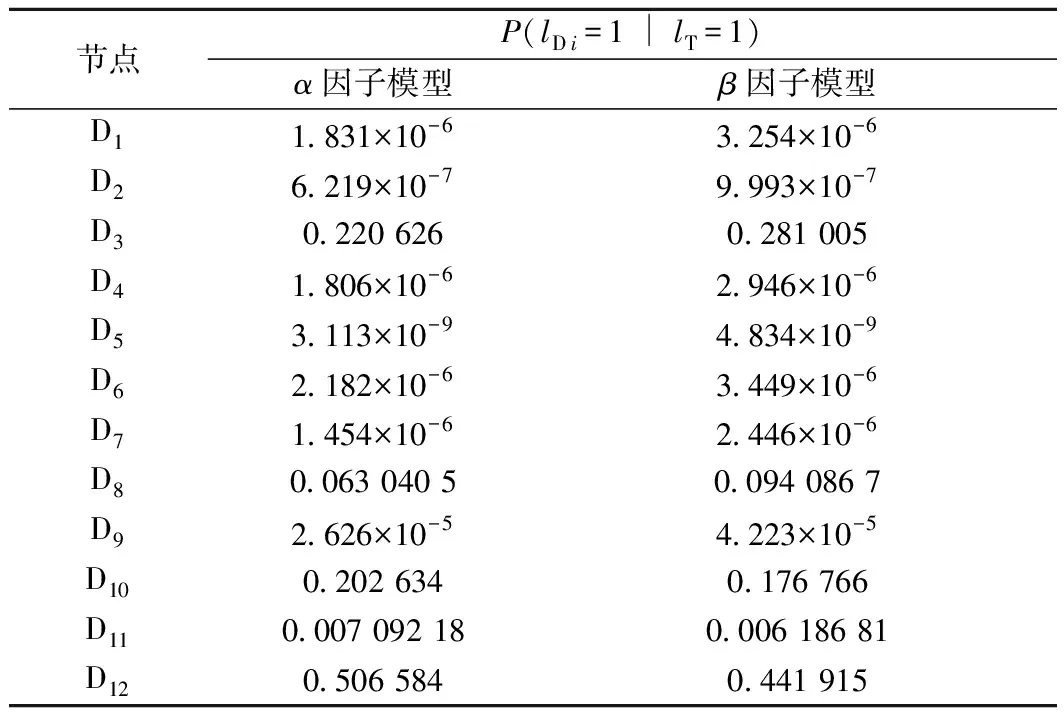
表6 系统故障时各单元的后验概率
5 结论
本文在考虑共因失效、系统降级运行和恢复机制等多种影响因素下,将贝叶斯网络模型引入列控车载子系统的可靠性分析中,得到的分析结论如下:
(1) 根据BN正向推理,得到系统可用度,并且当系统因故障降级运行时,系统的失效率更高,所以运营部门应尽量避免长时间、长距离处于这种故障降级状态,或者针对处于这种状态的车载子系统,需要有其他的应急备用措施。
(2) 根据BN反向推理,得到各单元模块的后验概率,为提高系统的可靠度,对DMI、BTM、BTM Ant、TIU、PROFIBUS总线等模块需要重点关注,它们是车载子系统的薄弱环节。
(3) 随着运行时间的延长,系统的可靠度会逐渐降低,且共因失效对系统的可靠度影响不可忽略。
(4) 由于β因子模型量化共因失效误差比α因子模型大,随着列控车载子系统设备故障数据的累积,通过α因子模型计算得到的系统可靠度更加符合实际情况。

