关于丢番图方程(44n)x+(117n)y=(125n)z*
冉银霞
(陇南师范高等专科学校 数信学院,甘肃 成县 742500)
设a,b,c为两两互素的正整数且满足a2+b2=c2.对于任意的正整数n,丢番图方程
(na)x+(nb)y=(nc)z
(1)
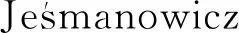

本文主要运用奇偶分析法、简单同余法以及二次剩余理论等方法讨论(a,b,c)=(44,117,125)时,方程(1)的解的情况,得到了如下结论:
定理1 对任意的正整数n,丢番图方程
(44n)x+(117n)y=(125n)z
(2)
仅有正整数解(x,y,z)=(2,2,2).
1 若干引理
引理1[3]设a,b,c满足a2+b2=c2.若z≥max{x,y},则丢番图方程ax+by=cz仅有整数解(x,y,z)=(2,2,2).
引理2[21]如果方程(1)有解(x,y,z)≠(2,2,2),则x,y,z各不相同.
引理3[22]设a,b,c是两两互素的正整数且满足a2+b2=c2.若丢番图方程ax+by=cz仅有整数解,则方程(1)没有满足z 引理4[23,24]设a,b,c是两两互素的正整数且满足a2+b2=c2,且2|b.用d2b表示b中2的最高幂指数.若a,c≡±1(modb/2或d2b),则丢番图方程ax+by=cz仅有正整数解(x,y,z)=(2,2,2). 引理5 丢番图方程 44x+117y=125z (3) 仅有正整数解(x,y,z)=(2,2,2). 证明因为44=22×11,117≡125≡1(mod 2),所以由引理4知,44x+117y=125z仅有正整数解(x,y,z)=(2,2,2). 引理6 不定方程125z1-32y1=22x-1没有整数解. 证明对方程两边模 5得:-(-1)y1≡22x-1(mod 5),然而由2α模5是周期为4的序列,其余数为1,2,-1,-2知:22x-1≡±1(mod 5)是不可能的.因此,不定方程125z1-32y1=22x-1没有整数解. 引理7 不定方程125z1+32y1=2·11x没有整数解. 证明2y1模11是周期为10的序列,其余数为1,2,4,8,5,-1,-2,-4,-8,-5.所以,若2|y1,则2y1≡1,4,5,-2,-8(mod 11);同样,22z1≡1,4,5,-2,-8(mod 11).对方程两边模11 得:22z1+(-2)y1≡0(mod 11),但当2|y1时,22z1+(-2)y1≡22z1+2y1≡0(mod 11)是不可能的;当2⫮y1时,22z1+(-2)y1≡22z1-2y1≡0(mod 11)显然也是不可能的. 因此,不定方程125z1+32y1=2·11x没有整数解. 根据引理1,2,3和引理4,只需研究(2)在n≥2且min{x,y} 情形1x>z>y.此时方程(2)可化为 117y=nz-y(125z-44xnx-z). (4) 由于z>y,故gcd(n,117)≠1.设n=32u13vn1,u+v≥1,gcd(n1,117)=1,则此时式(4)成为 32y13y=32u(z-y)13v(z-y)n1z-y(125z-44x32u(x-z)13v(x-z)n1x-z), (5) 由此可见n1=1. 情形1.1 若n=32u(u≥1),则2y=2u(z-y).于是(5)可化为 44x32u(x-z)=125z-13y. (6) 对式(6)取模11,有22z-2y≡0(mod 11),得22z-y≡1(mod 11),于是有10|2z-y,从而y≡2z≡0(mod 2).对式(6)取模3,有0≡(-1)z-1(mod 3),得z≡0(mod 2).故y与z均为偶数. 令y=2y1,z=2z1,则由式(6)得 22x11x32u(x-z)=(125z1-13y1)(125z1+13y1). (7) 注意到gcd(125z1-13y1,125z1+13y1)=2,因此由4|125z1-13y1知, 22x-1|125z1-13y1. 若11|125z1-13y1,则22x-111x|125z1-13y1,但 22x-111x>22z1112z1=484z1>125z1-13y1不可能.所以此时方程(7)没有整数解. 若11|125z1+13y1,3|125z1+13y1,则 125z1-13y1=22x-1. (8) 对式(8)取模3,得(-1)z1-1≡(-1)2x-1≡-1(mod 3),即(-1)z1≡0(mod 3),但这是不可能的. 若11|125z1+13y1,3|125z1-13y1,则 125z1+13y1=2·11x,125z1-13y1=22x-1·32u(x-z). (9) 对(9)第一式取模11,得4z1+2y1≡0(mod 11),即2y1≡-4z1(mod 11),因此有 22z1-x≡-1(mod 11),2z1-x≡5(mod 10). 对(9)第二式取模3,得(-1)z1≡1(mod 3),故有2|z1. 对(9)第一式取模3,得(-1)x+1≡(-1)z1+1≡2≡-1(mod 3),于是x≡0(mod 2).但由2z1-x≡5(mod 10)知x为奇数,矛盾.因此式(9)不成立. 情形1.2 若n=13v(v≥1),则y=v(z-y).于是(5)可化为 44x13v(x-z)=125z-32y. (10) 对式(10)取模8,有5z-1≡0(mod 8),得z≡0(mod 2);对式(10)取模11,有4z≡(-2)y(mod 11).设z=2z1,则有42z1≡5z1≡(-2)y(mod 11). 2y模11是周期为10的序列,其余数为1,2,4,8,5,-1,-2,-4,-8,-5;5y模11是周期为5的序列,其余数为1,5,3,4,-2. 若2⫮y,则5z1≡(-2)y≡-2y≡-1,-4,-5,2,8(mod 11),对比余数发现,这是不可能的.因此2|y. 令y=2y1,z=2z1,则式(10)变成了 22x·11x·13v(x-z)=(125z1-32y1)(125z1+32y1). (11) 注意到gcd(125z1-32y1,125z1+32y1)=2,因此由4|125z1-32y1知,22x-1|125z1-32y1.若11|125z1-32y1,则22x-111x|125z1-32y1,但22x-111x>22z1112z1=484z1>125z1-32y1,所以此时方程(11)没有整数解. 若11|125z1+32y1,13|125z1+32y1,则 22x-1=125z1-32y1. (12) 若11|125z1+32y1,13|125z1-32y1,则 125z1+32y1=2·11x. (13) 根据引理6和引理7知,方程(12),(13)均没有解. 因此,方程(10)没有整数解. 情形1.3 若n=32u13v(u≥1,v≥1),则y=u(z-y)=v(z-y).于是(5)可化为 11y13y=11u(z-y)13v(z-y)(145z-24x11u(x-z)13v(x-z)), (14) 从而y=u(z-y)=v(z-y),于是(14)可化为 44x32u(x-z)13v(x-z)=125z-1. (15) 对式(15)模3,有(-1)z-1≡0(mod 3),得z≡0(mod 2).令z=2z1,则(15)变为 (125z1+1)(125z1-1)=22x·11x·32u(x-z)·13v(x-z). (16) 情形2y>z>x.此时方程(2)可化为 44x=nz-x(125z-117yny-z). (17) 设n=2r11sn1,r+s≥0,gcd(n1,22)=1,则此时式(17)成为 22x11x=2r(z-x)11s(z-x)n1z-x(125z-117y2r(y-z)11s(y-z)n1y-z). (18) 由此可见n1=1,且有 125z-117y2r(y-z)11s(y-z)=22x-r(z-x)11x-s(z-x). (19) 情形2.1 若r=s=0,则由式(19)得 44x+117y=125z. (20) 由引理5知(20)仅有解(x,y,z)=(2,2,2),与y>z>x矛盾. 情形2.2 若r=0,s>0,则由式(19)得x=s(z-x),且有 125z-22x=32y11s(y-z)13y. (21) 对(21)模3得(-1)z-1≡0(mod 3),从而2|z. 令z=2z1,则式(21)变为 (125z1-2x)(125z1+2x)=32y11s(y-z)13y. (22) 注意到gcd(125z1-2x,125z1+2x)=1,则有13y|125z1-2x,或13y|125z1+2x,但13y>13z=132z1=169z1>125z1+2x>125z1-2x,不可能. 所以式(22)不成立. 情形2.3 若r>0,s=0,则由式(19)得2x=r(z-x),且有 125z-11x=2r(y-z)32y13y. (23) 对(23)模3得(-1)z≡(-1)x(mod 3),故z≡x(mod 2). 对(23)模13得23z≡(-2)x(mod 13). 若x≡0(mod 2),则23z≡2x(mod 13),即有23z-x≡1(mod 13),故12|3z-x,从而z≡0(mod 2).令x=2x1,z=2z1,则式(23)变为 (125z1-11x1)(125z1+11x1)=2r(y-z)32y13y. (24) 注意到gcd(125z1-11x1,125z1+11x1)=2,因此有13y|125z1-11x1,或13y|125z1+11x1,但13y>13z=132z1=169z1>125z1+11x1>125z1-11x1,不可能. 所以式(24)不成立. 情形2.4 若r>0,s>0,则由式(15)得2x=r(z-x),x=s(z-x),且有 125z-1=2r(z-y)32y11s(y-z)13y. (25) 对(25)模3得(-1)z≡1(mod 3),于是z≡0(mod 2).因1252-1≡0(mod 7),所以125z-1≡0(mod 7),但2r(z-y)32y11s(y-z)13y≢0(mod 7).因此式(25)不成立. 综上,对任意的正整数n,丢番图方程(44n)x+(117n)y=(125n)z仅有正整数解(x,y,z)=(2,2,2).2 定理1的证明