具有非线性自食的L-V竞争系统局部稳定性研究具有非线性自食的L-V竞争系统局部稳定性研究

雷朝铨，刘楚蕾 ，许丽莉

(1.宁德师范学院 福建宁德 352100；2.厦门大学 福建厦门 361005)

自然界中，物种同类相食是一种很常见的现象，这可能是由于缺乏食物等原因引起的。已经有很多学者提出各种具有自食的生态种群模型[1-6]，并对模型展开研究，但大部分工作都是假设自食是线性的。2016年ALADEEN等学者[7]才提出具有非线性自食的Leslie-Gower捕食—食饵模型，并研究了模型的动力学行为。受文献[6]启发，笔者提出如下具有非线性自食的Lotka-Volterra竞争模型：

(1)

令(x(t),y(t))表示系统满足初值条件x(0)>0,y(0)>0的解，且只考虑系统在Ω0={(x,y)∈R2|

x≥0,y≥0}上的动力学行为。易证系统(1)的解是正且有界的。

1 平衡点的存在性

系统(1)的平衡点满足以下方程组：

(2)

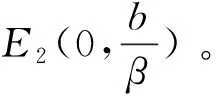
(3)

将式(3)化为

αx2-(r+c1-c-αd)x-d(r+c1)=0。

(4)

得到式(4)的判别式

Δ1=(r+c1-c-αd)2+4αd(r+c1)>0。

(5)

系统的正平衡点满足方程组：

(6)

Ax2+Bx+C=0。

(7)

其中，A=mn-αβ,B=d(mn-αβ)+β(r+c1-c)-mb,C=d[β(r+c1)-mb]。

而式(7)的判别式为

Δ=[β(r+c1-c)+d(mn-αβ)-mb]2-

4d(mn-αβ)[β(r+c1)-mb]

=[β(r+c1-c)-d(mn-αβ)-mb]2-4cdβ(mn-αβ)。

(8)

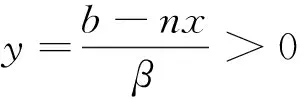
(9)

根据A的正负，分以下几种情形对正平衡点展开讨论。

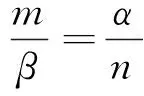
因此，当

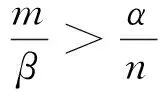
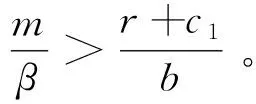
定义函数f(x)=Ax2+Bx+C，则有

(10)

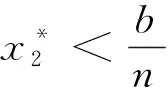
因此，当

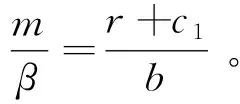
因此，当

因此，当

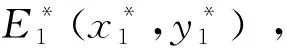
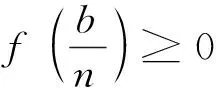
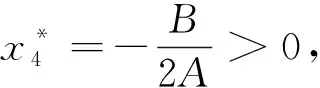
因此，当(H7)，(H8)，

(H10)

Δ=0,

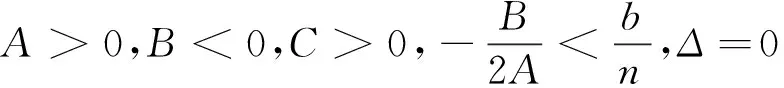
因此，当(H4)，(H7)，(H8)，(H11)，(H12)，

(H13)

Δ>0,

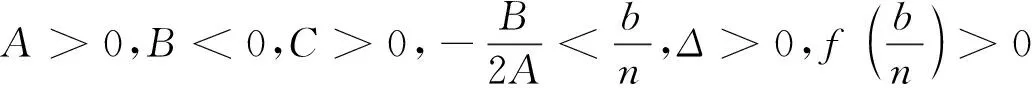
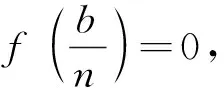
因此，当(H7)，(H8)，(H11)，(H13)，

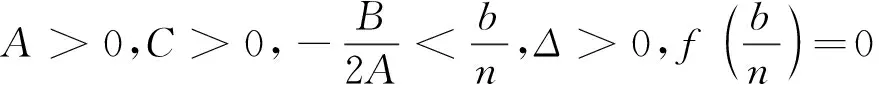
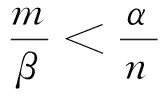
因此，当(H8)，(H9)，

2017年河北省非油气持证矿山企业综合利用产值17.86亿元，较上年增加10.4亿元；实现矿产品年销售收入506.25亿元，较上年增加107.33亿元；实现利润总额69.28亿元，较上年增加40.87亿元。

综上所述，得到如下结论。

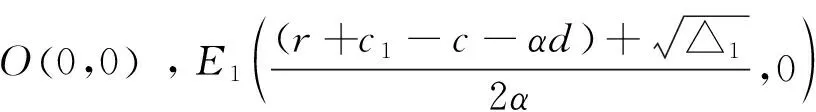
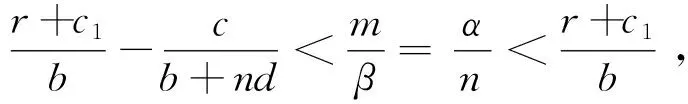
(2)若满足以下条件之一：

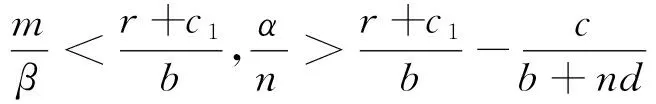
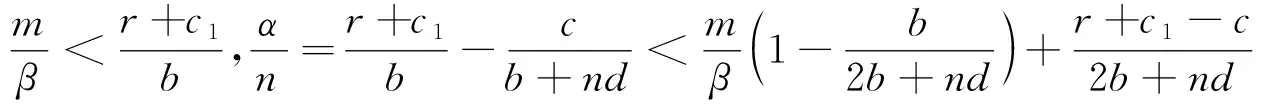
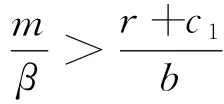
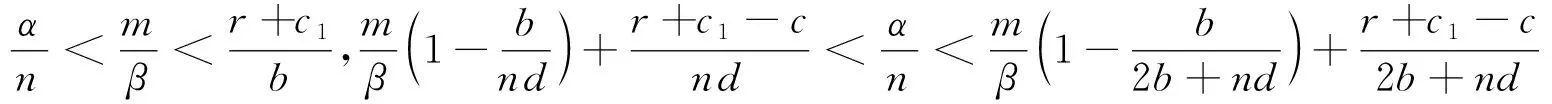
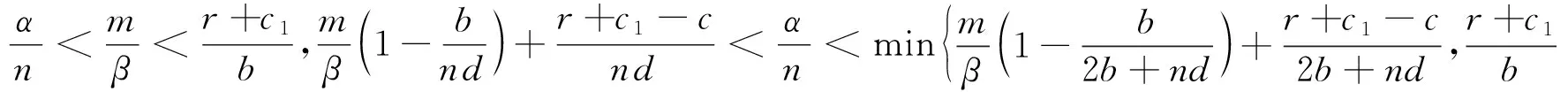
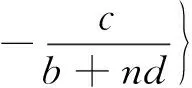
(7)若系统均不满足(1)-(6)的条件，则系统不存在正平衡点。

2 平衡点的局部稳定性

系统(1)的Jacobi行列式为

(11)

定理2 在系统(1)中，E0(0,0)始终是一个不稳定结点。

证明系统在平衡点E0(0,0)处的Jacobi行列式为

J(E0)的特征值为λ1=r+c1>0，λ2=b>0，因此E0(0,0)始终为不稳定结点。

证毕。

定理3 在系统(1)中，

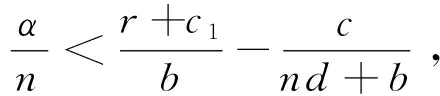
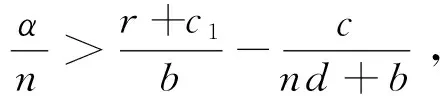
证明由于x1满足(3)式，因此系统在平衡点E1(x1,0)处的Jacobi行列式为

定义函数g(x)=αx2-(r+c1-c-αd)x-d(r+c1)，可知x1是g(x)唯一的正零点。

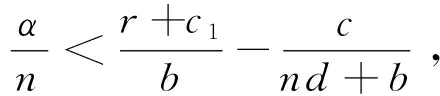
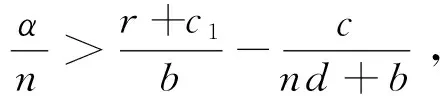
证毕。

定理4 在系统(1)中，

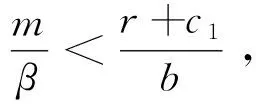
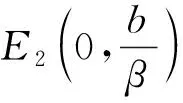
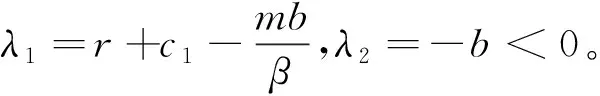
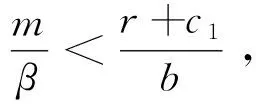
证毕。

定理5 在系统(1)中，

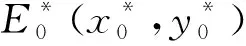
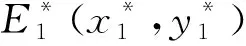
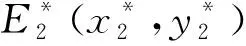
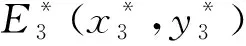
证明：为便于讨论，将系统的正平衡点统一记为E*(x*,y*)。由于正平衡点满足式(6)，因此系统在正平衡点E*(x*,y*)处的Jacobi行列式可化简为

(12)

则

由Routh-Hurwitz判据可得，正平衡点E*(x*,y*)是局部渐近稳定的充要条件为DetJ(E*)>0，即

cdβ-(x*+d)2(mn-αβ)>0。

(13)

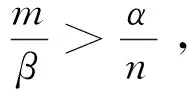
(-B+2dA)(x*+d)-2cdβ<0,

(14)

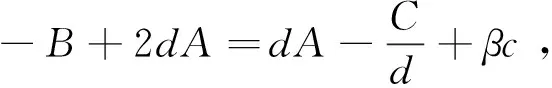
当Δ>0时，有

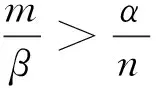
3 结论

众所周知，经典的Lotka-Voterra竞争模型至多有4个平衡点，其中正平衡点最多1个，本研究表明，考虑自食之后，系统的正平衡点具有多种情形，适当条件下可以有0、1或者2个，特别有2个正平衡的情形下，有一个是局部渐近稳定的，一个是不稳定的，也就是说，在这一情形下，正平衡点不可能是全局稳定的，这是与Lotka-Volterra竞争模型完全不一样的动力学行为。

本研究只探讨了该系统的平衡点的存在性和局部稳定性，在后续工作中将对系统的全局动力学行为展开研究。