一类多因子利率模型及其性质
徐 麒,胡良剑
(东华大学 理学院,上海 201620)
现代利率期限结构模型分为静态和动态两类。静态模型可根据某个时点的信息,通过特定的标准对该时点的利率期限结构进行拟合得到。动态模型则是从时间和期限两个维度用时间序列或随机微分方程来刻画利率期限结构的动态特征。在现代利率期限结构中,学者们对即期利率模型进行了大量的研究,得出了很多基于随机微分方程的经典模型。本文围绕即期利率的动态模型展开研究。
即期利率动态期限模型最早是由Merton[1]提出,他假定零息债券与股票的价格服从几何布朗运动。虽然该模型的方程形式简单,且漂移项与扩散项都是常数,但这对随机微分方程在利率模型中的应用起到了开创性作用。1977年Vasicek[2]提出了一个满足均值回复特性的即期利率期限结构模型,该模型中即期利率被设定为一个连续的马尔可夫过程,不足之处在于即期利率有可能是负数。Cox等[3]于1985年进一步提出了CIR(Cox-Ingersoll-Ross)模型,其漂移项具有均值回复性质,但其扩散项不再是常数,这确保了利率的取值为正。1991年Fong等[4]将Vasicek模型扩展到了两因素的情形,该模型在原来的即期利率动态模型中增加了波动率方程。上述单因子利率模型的漂移项均为线性形式,Ait-Sahalia[5]将单因子利率模型的漂移项与扩散项进行推广,提出了一个高度非线性的随机微分方程。戴璐等[6]讨论了Ait-Sahalia模型的解析性质,并证明了其数值解的收敛性。李艳军[7]将跳跃性引入到这类随机微分方程中,并对其解析性质进行了深入研究。此外,学者们对即期利率模型进行了扩展,主要包括延迟模型、仿射模型、多因子模型等,并且将其应用到实证分析中[8-11]。景智生[12]基于马尔科夫蒙特卡洛方法对中国动态利率期限结构进行研究。通过梳理总结近几年关于利率期限结构的文献发现,中国经济市场由于情况复杂,受到多重因素的影响,故采用多因子即期利率模型进行拟合将取得更好的效果。同时对于即期利率的波动率方程而言,当漂移项与扩散项均为非线性时,能够描述出更加客观的即期利率波动情况。本文对Fong-Vasicek模型作进一步扩展,并借用Ait-Sahalia模型的非线性特点刻画即期利率的波动情况,提出一个高度非线性的多因子即期利率模型,同时在理论上对其解的存在唯一性、矩有界性和Euler-Maruyama数值解的收敛性进行讨论,最后用MATLAB软件对其进行数值模拟,以验证该模型在利率市场上的可行性。
1 预备知识
1.1 相关符号及主要定理
在本文中如果没有特别说明,则采用如下记号:
(Ω,F,P)为完备概率空间,{Ft}t≥0为满足通常条件的σ代数流。
IA为集合A的示性函数。
Lp(Ω;Rd)为p次可积的d维随机变量。



C2, 1(R×R+;R)为在x∈R上二阶连续可微、在t∈R+上一阶连续可微的全体二元函数V(x,t)。

dx(t)=f(t)dt+g(t)dWt
(1)

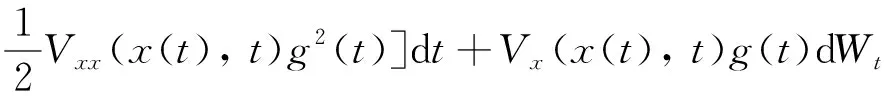
(2)
1.2 典型的利率模型
(1) Vasicek模型[2]为
dRt=α(μ-Rt)dt+σdWt
其中:α、μ和σ均为非负常数;μ为利率的长期均值。由漂移项α(μ-Rt)可知,利率Rt在均值μ上下波动。该模型最大的缺点是Rt的取值可能是负值,无法满足市场的非负性。
(2) CIR模型[3]为
其中:α、μ和σ均为非负常数;μ为利率的长期均值。该模型有效克服了Vasicek模型的缺点,即保证了利率的非负性。
(3) Ait-Sahalia模型[5]为


(4) Fong-Vasicek模型[4]为

2 模型建立及其性质分析
一个模型是否能有效模拟实际利率,关键是看这个方程是否具备“良好”的性质。这些性质通常包括非负解的存在唯一性、方程解的矩有界性、数值解的收敛性等。对Fong-Vasicek模型作进一步扩展,提出的模型形式如式(3)和(4)所示。
(3)
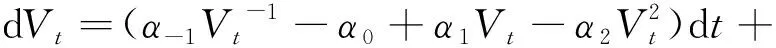
(4)
式中:λ,μ≥0;αi≥0,i=-1, 0, 1, 2;βj≥0,j=0, 1, 2;β3>1。
2.1 解的存在唯一性
定理2.1对于任意初值V0>0且R0>0,Vt,Rt在t≥0时存在唯一的全局正解。
证明:由式(4)可知波动率Vt满足Ait-Sahalia模型,而该模型全局正解的存在唯一性在文献[5]中已被证明,故本文只需讨论Rt的解。用常数变易公式[13]对式(3)进行处理可得,对任意t>0,

(5)
其中
显然

即结论成立,该模型存在唯一的全局正解。
2.2 解的矩有界性
若无特殊说明,以下提到的Ki,Mi,Hi,i=1, 2, 3,...均为与t无关的正常数。
定理2.2对于随机微分方程
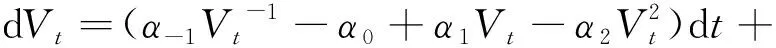
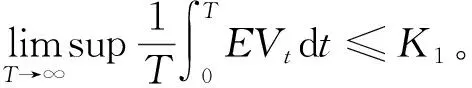
证明:定义函数φ:(0, +∞)→[0, +∞)为
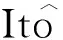
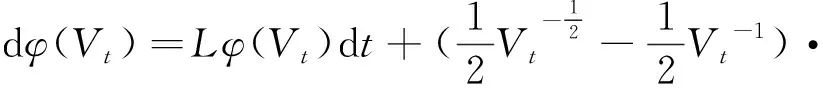
(6)
其中
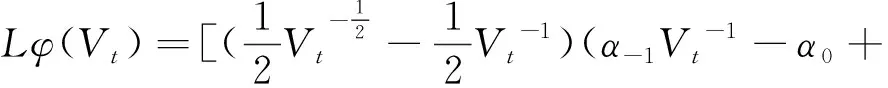
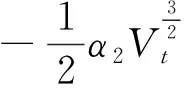
由参数条件和多项式的有界性[14]可知,必存在一个常数K1,使得
Lφ(Vt)+Vt≤K1
对上式两边先取定积分再取期望,得到


故

易得φ(x)≥0,故Eφ(VT)≥0。则可以得到

当T→∞时,
(7)
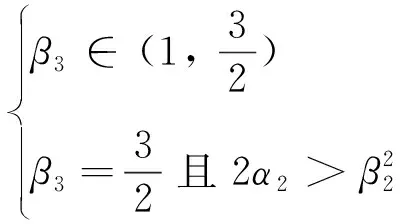
两者之一时,Vt的二阶矩有界。
证明:取U2(t)=etVt2
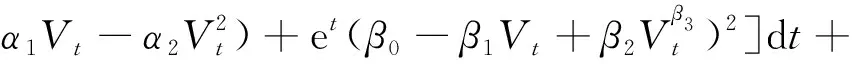
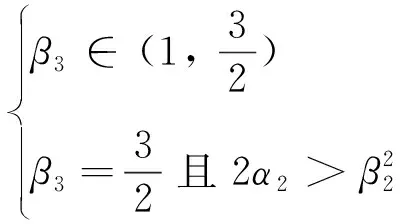
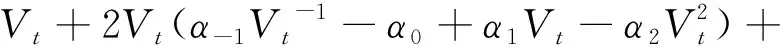
故可以得到
etE(Vt2)≤V02+K2(et-1)
即
E(Vt2)≤(V02-K2)e-t+K2
(8)
结合定理2.3,根据Chebyshev不等式[13]可得:
推论2.1在定理2.3的条件下,Vt的一阶矩有界[13]。
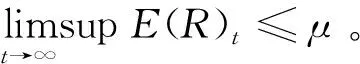
证明:令Yt=eλtRt,故有
∀k>0, 定义停时ζk=inf{t:Rt≥k}

当k→∞时,由Fatou引理可得
E(Rt)≤e-λtR0+μ(1-e-λt)
显然
(9)
定理2.5在定理2.3的条件下,设T>0, 对于任意t∈[0,T],Rt的二阶矩有界。
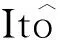


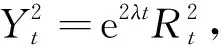
由Gronwall不等式可得:
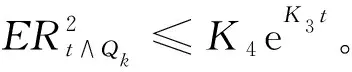
(10)
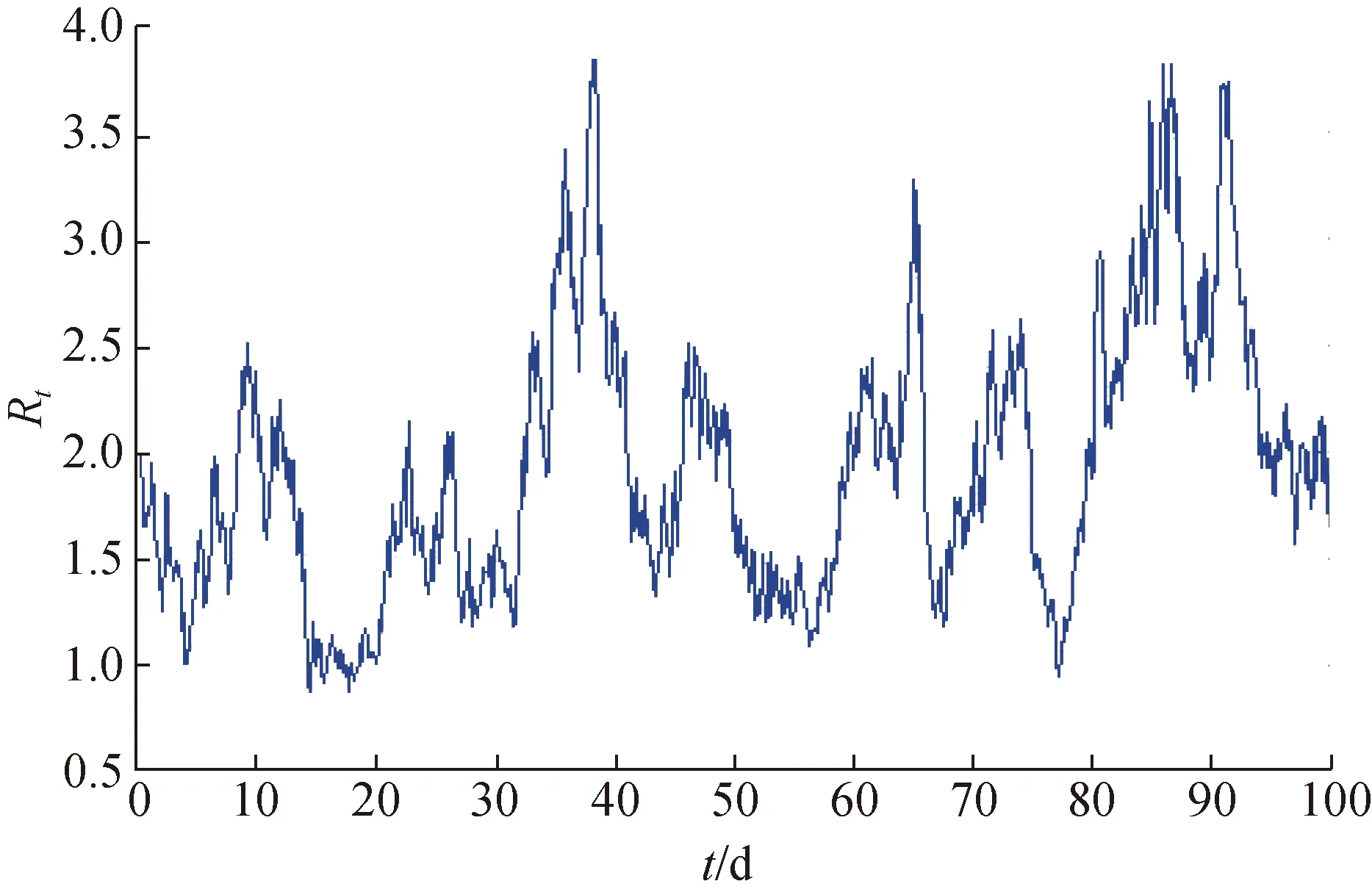
即对于∀0 由于方程式(3)和(4)没有显式解,故需要证明其数值解的收敛性,采用的方法为Euler-Maruyama(EM)方法。 当随机微分方程的扩散项和漂移项满足全局Lipschitz条件时,其数值解收敛到解析解[15]。但由于本文模型不满足全局Lipschitz条件,故不可以直接用此结论,需要对其作进一步证明。 首先,对于方程 令 f(x)=α-1x-1-α0+α1x-α2x2 g(x)=β0-β1x+β2xβ3 对于给定的足够小的步长Δ,节点tn=nΔ和初始值v0=V0>0, 则方程的离散EM逼近解为 vn+1=vn+f(vn)Δ+g(vn)ΔWn (11) (12) 故对应连续的函数逼近可以定义为式(13)所示的形式。 (13) 同理,可由式(3)得到Rt的离散EM逼近解、阶梯过程和对应连续的函数逼近如式(14)~(16)所示,其中r0=R0。 (14) (15) (16) 式中:ΔBn=B(tn+1)-B(tn)是布朗运动增量,且因为数值解并不一定能完全保持真实解的非负性,故在vn上增加绝对值以保证根号有意义。 定理3.1对任意的正常数T>0,有 证明: 第1步:对于任意的p>0,k>0,定义停时 其中,φ(x)即为定理2.2中所定义的函数。 因为停时保证了vt>0, 故在以下分析中,不再加绝对值。 同理, 故 (17) 第2步:取停时zk=ak∧bk,则 3J1+3J2+3J3 由引理3.1,可得: 令h1为正常数,当k充分大时, (18) 第3步:取任意小的ξ∈(0, 1)定义 故 当Δ充分小时, 故可以得到 (19) 对本文中第2节提出的利率模型(3)和(4)进行数值模拟。根据第3节中的定义将此模型按EM方法离散化,得到 (20) (21) 式中:εn、ηn均为均值为0和方差为Δ的正态独立同分布序列。假定该模型的参数为λ=0.2,μ=0.018,α-1=0.000 130 4,α0=0.004 643,α1=0.043 33,α2=0.114 3,β0=0.000 110 8,β1=0.001 883,β2=0.009 681,β3=1.25(其中:αi,i=-1, 0, 1, 2;βj,j=0, 1, 2, 3设置均引自文献[5])。同时,设置T=100,Δ=0.1,根据这些参数,用MATLAB软件进行数值模拟,结果如图1所示。 图1 r0=0.02,v0=0.05时模型的数值模拟图Fig.1 Simulation of the model process when r0=0.02, v0=0.05 由图1可知,模型(3)和(4)满足利率模型的一般性质,主要为正解的存在唯一性以及数值解的收敛性等。此外,该模型具有均值回归的特点,Rt随着均值μ的变化上下波动,但整体上并没有偏离均值。这些参数之间的关系均满足第2节矩有界性中的参数条件,从而能证明矩有界性。 采用一个二维非线性的随机微分方程对利率进行描述,证明了该模型全局正解的存在唯一性和矩有界性,同时还对其EM数值解的收敛性进行理论证明。在证明该模型解析性质后,利用MATLAB软件对其进行数值模拟,得到的结论与本文第2、3节所证明的性质相符合。研究结果表明,该模型可以被用于描述利率或其他金融变量的动态变化,具有实际意义。3 数值解的收敛性
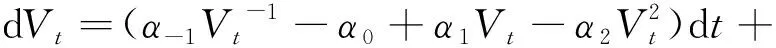


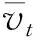

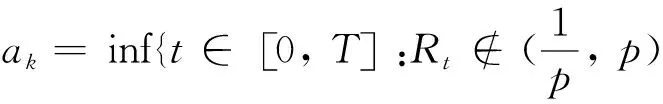

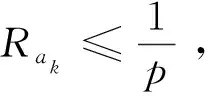


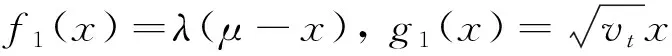


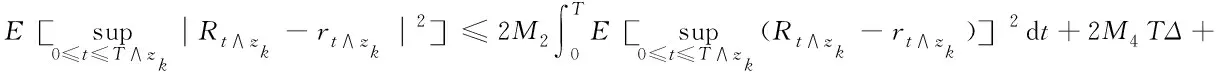



4 数值模拟

5 结 语

