考虑可靠度的桥式起重机主梁金属结构稳健优化设计

翁飞翔， 郑 成， 王庆霞

(东华大学 机械工程学院，上海 201620)

起重机作为一种搬运机械，在工业生产中占据着重要的地位。但国内的桥式起重机(简称“桥机”)存在着材料浪费问题[1]，即采用更大的结构尺寸来保证较高的强度、刚度、可靠度等。此外，由于金属结构占桥机60%～80%的质量，所以在保证安全使用的前提下实现桥机金属结构的轻量化，可以大幅度减少成本。目前桥机金属结构的优化设计的相关研究与应用存在着局限性。程丽珠[2]针对桥机主梁进行分析和优化，但在分析中将各结构参数及载荷看作定值。这种研究仍停留在传统的结构优化上，即基于确定性条件进行优化，忽略了参数在实际条件下的变化，难以保证结果可靠。孟文俊等[3]采用可靠性分析对可靠度影响较大的参数设为设计变量并进行确定性优化，但未实现可靠性优化。杜习超等[1]考虑桥机主梁截面参数和载荷的随机性，建立可靠性优化模型并进行优化设计，在一定程度上考虑随机性，但设计结果往往处于边界条件，因此不具备稳健性。Fan等[4]基于有限元仿真数据建立桥机性能函数的Kriging代理模型，并将其用于可靠性优化设计，虽然满足所有可靠性要求，大大提高计算效率，但还是未将稳健性纳入设计之中。稳健性作为一种衡量产品敏感度的参数，对产品的安全性具有较大影响，因此近年来诸多学者对稳健设计方法进行研究，并取得了一定成果。张英等[5]在确定性优化的基础上，结合响应面近似模拟技术、蒙特卡洛法和6σ稳健优化设计理论，构建桥机的稳健优化模型，并采用自适应模拟退火算法进行求解，在降低桥机结构自重的同时，减小优化结果对设计变量及噪声波动的敏感性。Lee等[6]提出一种混合稳健优化方法，在建立的高频结构仿真模型的基础上，采用遗传粒子群优化算法更新设计变量，通过正交阵列的噪声测试评估结果，提高给定成本下的手机金属框架天线的稳健性。Yoon等[7]采用罚函数法解决传统田口方法的缺陷，提出一种有效的稳健优化方法，并将其用于无刷直流电油泵的设计，降低齿槽转矩及其脉冲波动，并提高这两者的稳健性。

可靠性与稳健性均能够在一定程度上影响桥机的工作能力与安全性能，所以综合可靠性和稳健性的轻量化设计具有极大的研究与应用价值。在保证桥机金属结构具备一定的可靠性和稳健性的条件下，减小结构重量，可以在很大程度上降低维修管理费用和人工成本，提高桥机的安全性。

本文以桥机作为研究对象，运用APDL语言建立整机的参数化模型并加以分析；根据确定性优化模型，利用OPT模块进行优化设计；在考虑各参数随机性的前提下，运用PDS模块对确定性优化结果进行可靠度分析；最后，建立考虑可靠度的桥机主梁金属结构稳健优化模型，采用MATLAB软件进行优化，在满足可靠度和稳健性条件下实现轻量化设计。

1 桥机金属结构建模分析

桥机主梁为箱梁结构，截面如图1所示。桥机额定起重量为125 000 N，主梁长度为22.5 m，运行大车基距为4.4 m，运行小车基距为2.4 m、轨距为2 m，吊钩重量为1 500 N，附属结构重量为50 000 N，小车重量为62 120 N。初始主梁的翼板厚度T1= 0.008 m，腹板厚度T2=0.006 m，腹板高度H0=1.35 m，腹板内壁间距B0=0.44 m。图1中的“B0+0.06”为翼板宽度，其中的0.06 m为翼板两侧的伸出总长度。

图1 主梁截面简图Fig.1 Schematic diagram of girder section

使用APDL语言在ANSYS软件中选择BEAM188单元建立桥机整体的参数化模型，其中包括438个节点和216个单元。起升状态级别为HC2，最危险工况为小车位于跨中满载下降制动，同时大车平稳制动。起重量、吊钩重量和小车重量以集中载荷的形式由小车车轮施加在主梁上，附加结构重量和桥机自身重量以均布载荷的形式施加，端梁两端均采用铰接约束。最危险工况下桥机金属结构的变形和等效应力云图如图2所示。

由图2可知，主梁实际最大挠度Dmax为图2(a)显示的最大挠度值减去主梁端部的变形值，即Dmax=0.018 21 m，最大等效应力σmax=94.9×106Pa。根据GB/T 3811—2008[8]，结构材料Q235的控制应力为140.3×106Pa，许用挠度为0.030 m。

由此可见，主梁的强度、刚度在最危险工况下均符合要求，且有较大安全余量，即其结构存在优化空间，从而实现减重。

(a) 变形图

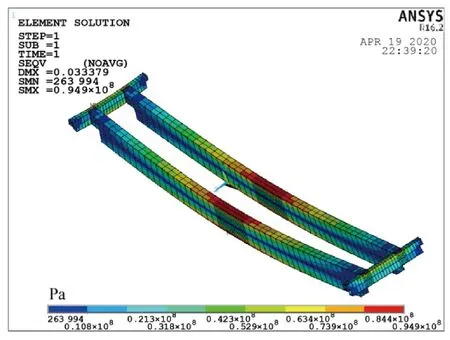
(b) 等效应力云图

2 桥机主梁确定性优化

2.1 确定性优化模型

对于桥机主梁截面，选择腹板高度、腹板内壁间距、翼板厚度、腹板厚度作为设计变量，以桥机金属结构总体积V最小为目标，控制约束条件如下：

(1)

式中：[δ]为许用挠度，[δ]=0.030 m； [σ]k为控制应力，[σ]k=140.3×106Pa；σs为屈服应力，σs=235×106Pa。

表1 几何约束参数Table 1 Geometric constraint parameters m

2.2 优化结果及分析

运用ANSYS的OPT模块对2.1节优化模型进行优化设计，优化算法选择为ANSYS自带的零阶算法，优化结果如表2所示。体积优化迭代过程如图3所示，共迭代49次，最优解出现在第49次迭代。

表2 设计变量优化结果Table 2 Optimization result of design variables m

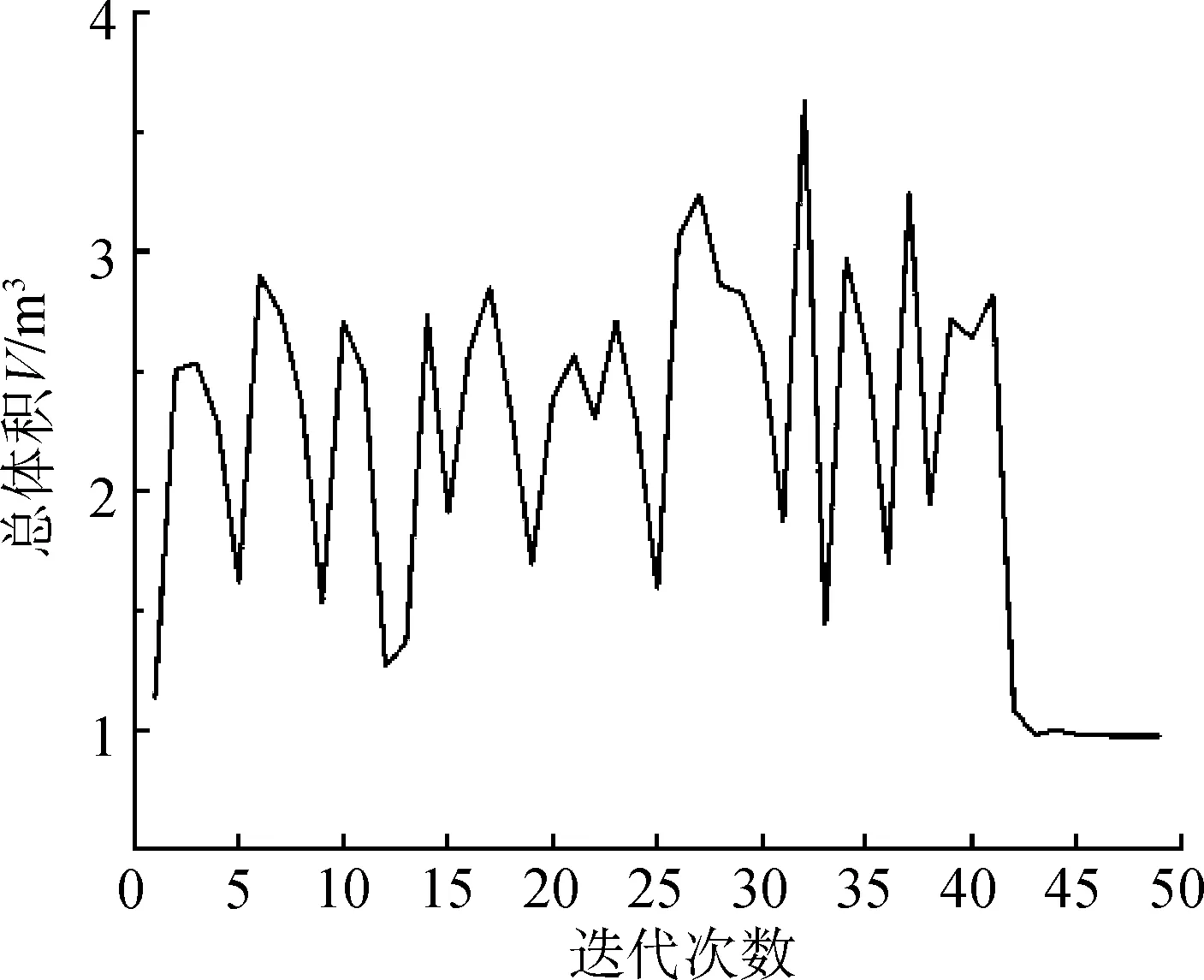
图3 体积优化迭代过程图Fig.3 Iteration process diagram of volume optimization

优化完成后，由于考虑到实际制造加工的限制要求，对设计变量优化结果进行圆整。T1和T2圆整时以0.002 m为间隔，B0宜取为0.01 m的倍数，H0化整时尾数取为0.05 m的倍数[9]。根据圆整的设计变量优化结果，通过ANSYS软件分析得到：主梁的最大应力为120.2×106Pa，小于控制应力[σ]k，跨中最大挠度为0.027 82 m，小于许用挠度[δ]，满足GB/T 3811—2008[8]对强度和刚度的要求，同时实现主梁体积下降11.98%。

3 桥机主梁可靠性分析

确定性优化将设计变量当作一个确定值，并未考虑制造、环境等影响参数的可变性、随机性，所以设计结果难以保证可靠性，因此有必要对设计结果进行概率分析，验算其可靠性。

3.1 可靠性分析法

3.1.1 结构可靠度

结构的可靠度为在规定时间内和规定条件下结构完成预期功能的概率。结构是否能完成各项功能则由其极限状态来衡量。为了描述结构的极限状态而引入功能函数，若X=[x1，x2，…，xn]为影响结构某功能的随机变量，则定义该功能的函数Z为

Z=g(X)=R(X)-S(X)

(2)

式中：R(X)为抗力；S(X)为载荷效应。

由式(2)可知，结构某功能的可靠度即Z≥0的概率。

3.1.2 蒙特卡洛法(Monte Carlo method， MCM)

MCM是一种概论分析方法，在建立的功能函数上通过对随机变量进行抽样，计算功能函数值，得到目标概率。MCM主要依据统计学中的两个基本定律，即切比雪夫大数定律和伯努利大数定律，所以MCM在样本足够时具有较高精度，同时其收敛性与变量维度无关，可以依靠计算机的强大计算能力抽取足够的样本总数，从而计算出具有较高精度的可靠度。

根据MCM，可靠度(r)的计算式为

(3)

式中：N0为抽样总数中满足式(2)中Z≥0的个数；n为抽样总个数。

3.2 随机参数确定

(1) 几何模型参数。由于现代加工手段以及装配手段等都不具备绝对的准确性，所以几何参数应当做随机量考虑[3]。将公称尺寸定义为变量均值，按照3σ原则，取Δx/3为标准差，其中Δx与加工方法有关，冷轧取Δx1=0.000 25 m，火焰切割取Δx2=0.001 50 m[10]。

(2) 材料属性参数。目前我国钢材的屈服强度(σs)一般只能保证其中90%不小于规定值，即屈服强度的变异系数Vc=0.05，弹性模量(E)和密度(ρ)的变异系数Vc=0.03[10]。

(3) 起升载荷参数。参照同类起重机的使用数据，起升载荷的均值系数为0.467，标准差系数为0.308[1]。同时，采用0.05的显著性水平，桥机的起重量(P)可以接受对数正态的假设检验[11]。

各参数的分布信息如表3所示。

表3 随机变量的分布参数Table 3 The distribution parameters of the random variables

3.3 可靠性分析结果及分析

运用ANSYS的PDS模块，采用MCM下的拉丁超立方抽样进行概率设计，结果显示，在置信水平95%时，桥机主梁的刚度可靠度为95.982%，强度可靠度为99.673%。根据可靠度许用值为98%[1]，可见刚度可靠度未满足要求，说明了确定性优化难以满足可靠性的要求，所以有必要在优化设计中考虑可靠性。

4 考虑可靠度的桥机主梁稳健优化

4.1 考虑可靠度的稳健优化模型及其变换

4.1.1 考虑可靠度的稳健优化模型

目标函数为桥机主梁截面积(f1)，如式(4)所示。

f1=2[T1·(B0+0.06)+T2·H0]

(4)

参照上文中的约束条件式(1)，建立考虑可靠度的约束条件如下：

(5)

式中:[R]为许用可靠度，[R]=98%；Rδ为刚度可靠度，Rδ=P{[δ]-Dmax≥0}，Dmax如式(6)所示；Rσ为强度可靠度，Rσ=P{[σ]k-σmax≥0}，σmax如式(7)所示。

(6)

(7)

式中：Q为主梁上总的移动载荷，由起重量P、吊钩重量和小车重量构成；Iz为绕中性轴的惯性矩；Mmax为跨中最大弯矩，由起重量、吊钩重量、小车重量和自重引起；W为截面抗弯模量。

可靠度的计算采用MCM在MATLAB平台完成，抽样总数为600 000。

同时用灵敏度法[12]引入稳健设计目标函数附加项，减小目标函数对设计变量的灵敏度，从而实现稳健设计。这里构造仅考虑目标函数的附加项(f2)如下：

(8)

式中：xi为设计变量，即T1、T2、B0、H0；δi为设计变量的容差，此处分别取为0.001、 0.001、 0.005、 0.010 m。

最后联立式(4)、(5)、(8)，可得考虑可靠度的桥机主梁稳健优化设计模型为

(9)

4.1.2 数学模型变换

对于式(9)所示的多目标带约束问题，往往将其转换为单目标无约束问题后再优化求解。

首先运用评价函数法中的组合赋权法[13]将多目标函数构造成单目标函数如下：

f=w1·f1+w2·f2

(10)

wi=α·ai+(1-α)·bi(i=1， 2)

(11)

式中：f为无量纲的组合目标函数；α根据决策者的偏好信息来确定，取决于对赋权法的偏重，此处取为0.5；ai为主观权重，根据各目标的重要程度确定，a1=0.7，a2=0.3；bi为客观权重。

采用均差排序法[14]计算客观权重bi：

式中：ci为第i个目标关于各个极小点的离差，ci=fi(xj)-fi(xi)，(i≠j)；xi、xj分别为目标函数fi、fj的极小点。

将上述参数值代入式(11)得：w1=0.374 5，w2=0.625 5。

将w1和w2代入式(10)可得：

f=0.374 5·f1+0.625 5·f2

(12)

其次，构造外罚函数[15]去除约束条件(5)，则数学模型变为

minF=f+p

(13)

式中：F为外罚函数；p为惩罚值，当约束条件(5)中存在任意一个条件失效，p为一正数，否则p为零。

综上可知，最后的数学模型转变为求解单目标函数F的最小值。

4.2 模型求解及结果对比

在MATLAB软件平台上搭建GUI界面，采用基于改进遗传算法的粒子群算法对式(13)进行优化求解，结果如图4所示。

将图4中求得的最优点圆整：T1=0.008 m，T2=0.006 m，B0=0.430 m，H0=1.200 m。

图4 GUI下的迭代信息Fig.4 Iterative information under GUI

对圆整结果进行分析，桥机的最大应力为111.2×106Pa，最大挠度为0.024 46 m，刚度和强度可靠度分别为98.03%和99.86%，因此两者均满足要求，且实现主梁体积下降8.26%。

运用一阶灵敏度函数[16]求解结构参数对输出响应(刚度和强度)的灵敏度，即式(6)中的Dmax和式(7)中的σmax分别对结构参数T1、T2、B0、H0求偏导，结果如表4所示。

表4 设计结果的灵敏度对比Table 4 Comparison of design results’ sensitivity

由表4数据进行再计算可得，相比较确定性优化而言，考虑可靠度的稳健优化设计的刚度对T1、T2、B0、H0的灵敏度绝对值分别降低12.80%、11.88%、16.57%、16.10%，强度对T1、T2、B0、H0的灵敏度绝对值分别降低8.35%、13.15%、12.11%、12.28%。由此可见，考虑可靠度的稳健设计的灵敏度绝对值均实现不同程度的降低，且至少降低8.35%，即在一定程度上实现稳健目的。

5 结 语

针对桥机主梁进行了参数化建模，并在此基础上进行静力学分析与确定性优化，在对确定性优化结果进行可靠性分析时，发现其刚度可靠度未满足要求。于是将可靠度纳入约束条件，运用灵敏度法和蒙特卡洛法建立考虑可靠度的桥机主梁稳健优化模型，并采用评价函数法和外罚函数法对模型进行转化便于编程运算，最后通过智能优化算法进行求解。结果显示，在实现体积下降8.26%的同时，考虑可靠度的稳健优化的设计结果与确定性优化相比，前者各项灵敏度绝对值至少降低8.35%，且强度、刚度的可靠度分别为99.86%和98.03%，均大于可靠度许用值(98%)。由此表明，本文提出的考虑可靠度的稳健优化设计可以实现轻量化目的和可靠性要求，且在一定程度上达到稳健目的。由于在设计过程中考虑的随机变量并不充分，在后续的研究中可以引入更多的随机参数来完善优化设计，同时本文将随机参数视作独立变量，未考虑它们的相关性，后续的研究也可从这一方面做深入探讨。