基于PSO-RVM模型的光伏出力日前区间预测

王 粟， 隗磊锋， 曾 亮

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

太阳能作为清洁、可持续的能源之一，在世界各国中得到广泛应用，电力需求占比也越来越高。到2030年太阳能将占美国电力需求的14%，到2050年将占27%[1]。然而，大规模的光伏并网，给电网稳定性造成的影响也逐渐增加，因此对光伏发电进行预测也变得日益重要[2]。

根据现有的研究成果，光伏功率的预测可以分为两类：确定性估计和概率估计两大类[3]。文献[4]采用滚动时间窗的自适应BP神经网络对光伏功率进行预测。文献[5]采用灰狼群算法对SVM参数进行优化，并用优化后的模型对光伏功率进行预测。文献[6]通过提升回归树建立预测模型，对光伏功率进行预测，并采用随机森林对残差进行预测，两模型的预测值相加得到最终预测值。文献[7]通过自适应Kmeans对预测日进行聚类，并采用LSTM模型进行发电功率的预测。与上述确定性估计不同，区间预测能够在规定的置信水平对不确定度进行量化，表示可能的预测。由于预测的不确定性，具有预测精度指示的上下限范围比传统的预测点更可信，根据预测结果，如果准确地知道模型误差的概率分布，就可以准确地计算预测区间[8]。文献[8]提出一种基于EEMD和RVM的光伏功率区间预测，通过EEMD对功率序列进行分解，并采用样本熵(SE)对序列进行重构，重构的序列采用RVM进行预测，得到一定置信水平下的区间结果。文献[9]采用上下界法(LUBE)与极限学习机(ELM)相结合的方法，构造多输入两输出的区间预测模型，对光伏功率进行区间预测。文献[10]采用分位数回归森林计算任意分位点下的预测结果，并对预测值采用核密度估计得到概率密度预测。

文献[11]采用分位数LightGBM预测不同分位数的负荷值，通过核密度估计方法得到预测点的概率密度函数。

本文先对预测日进行相似日的筛选，将选出的相似日采用混合核相关向量机对光伏功率进行训练，并采用粒子群算法(PSO)对混合核的参数进行优化，利用优化后的模型进行预测，得到不同时刻的区间预测。试验结果表明，本文所提方法能够较好地预测出光伏输出功率的变化趋势以及区间范围。

1 建模原理

1.1 灰色关联分析与余弦相似系数

假设x=[x(1),x(2),…,x(n)]表示预测日特征，xi=[xi(1),xi(2),…,xi(n)]表示第i个历史日特征，x(j)与xi(j)表示预测日与历史日的第j个特征。则x(j)与xi(j)之间的关联系数可表示为

其中，ξ=|x(j)-xi(j)|，ρ常数取值为0.5。

因此，第i个历史日与预测日之间的关联系数可表示为

预测日x(j)与历史日xi(j)则之间的弦相似系数

由于灰色关联度反映的是历史日与预测日之间的总体相关性，余弦相似度反映历史日与预测日之间的变化趋势的相似性[12]。因此，本文采用灰色关联分析与余弦相似相结合选择相似日，其表达式为

Ri=αri+(1-α)Dcosi

其中α设为0.5。

1.2 相关向量机

相关向量机(Relevance Vector Machine, RVM)是由Tipping(2001)提出的具有高度稀疏性的贝叶斯学习方法[13]。给定训练样本xn和目标值tn,则RVM模型可定义为

式中：wi为模型权重，N为样本数量，K(x,xi)为核函数，ξn为服从N(0,σ2)的高斯分布。

假设目标值tn相互独立，则训练样本的似然函数

通过训练样本的似然函数和先验概率分布，利用贝叶斯公式，计算得权重的后验概率分布为：

式中，Σ=(σ-2ΦTΦ+A)-1，A=diag(a0,a1,…,aM)，μ=σ-2ΣΦTt为均值。

在给定的置信区间α下，区间预测结果可表示为：

其中U，L分别表示区间去测结果的上下限，Zα/2表示标准正太分布的双侧α分为点。

RVM算法的常用核函数主要有高斯核函数、多项式核函数以及Sigmoid核函数。不同的核函数都有各自的特点，对不同趋势数据的预测精度不同[15]。因此，选择高斯核函数和多项式核函数构造混合核函数。

高斯核函数表达式为：

多项式核函数表达式为：

K2(x,xi)=((x·xi)+r)q

组合和函数表达式为：

K=αK1+(1-α)K2

式中σ为核宽;r为常数，本文设为1;q为整数;α为权重。

1.3 粒子群算法

粒子群算法(Particle Swarm Optimization, PSO) 算法作为一种启发式优化算法。它只有两个参数，粒子的位置和速度，因此，具有数学分析简单、易于操作等优点[14]。在D维空间中第i个例子的空间位置为Xi=(xi1,xi2,…,xiD)T，速度为Vi=(vi1,vi2,…,viD)T，当前时刻的个体极值为Pibest，全局极值为gbest。粒子i在迭代过程中根据如下公式更新自己的位置和速度。

vij(t+1)=wvij(t)+α1+α2

xij(t+1)=xij(t)+vij(t+1)

式中，α1=c1r1(t)(pij(t)-xij(t))，α2=c2r2(t)(pgj(t)-xij(t)),i=1,2,…,N个粒子；j=1,2,…,D；c1，c2为学习因子；w为权重因子；r，r2为[0,1]之间的任意数。

2 基于PSO-RVM的光伏功率区间预测

图 1 基于PSO-RVM的光伏功率区间预测模型

基于PSO-RVM的光伏功率区间预测模型建模具体步骤为：

1)获取辐照度、温度、湿度、散射度等历史值，选择记录时间间隔为10 min的值。

2)通过灰色关联系数与余弦相似系数计算待预测日的相似日，并在筛选出来的相似日中选择相似度最高的前m天。

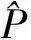
5)模型评估，采用平均绝对误差(MPE)、均方根误差(RMSE)、区间覆盖率(PICP)和区间宽度(PINAW)衡量系统的预测性能。

式中：Pmeas(i)为i时刻光伏功率实测值；Ppred(i)为i时刻光伏功率预测值;U和L分别为预测区间的上下限；N为选取的测试数据个数。

3 仿真算例分析

本文数据选择某电站每天(08：00-18：00)历史数据进行仿真。针对电站数据记录为5 min记录一次，因此，选择取样间隔为每10 min的数据进行仿真。为了验证所提PSO优化混合核RVM模型(简称模型3)的有效性，与高斯核RVM(简称模型1)和PSO优化的高斯核RVM(简称模型2)进行比较。选择不同的天气情况对模型进行了测试。同时，本文中采用MAE、RMSE、PINAW和PICP衡量系统的预测性能。

图2为不同天气的仿真图。表1为不同模型的预测值的RMSE、MAE；表2为不同模型分别在90%和80%置信区间下的预测PINAW和PICP。

(a)预测结果之一

(b) 预测结果之二

(c) 预测结果之三

(d) 预测结果之四

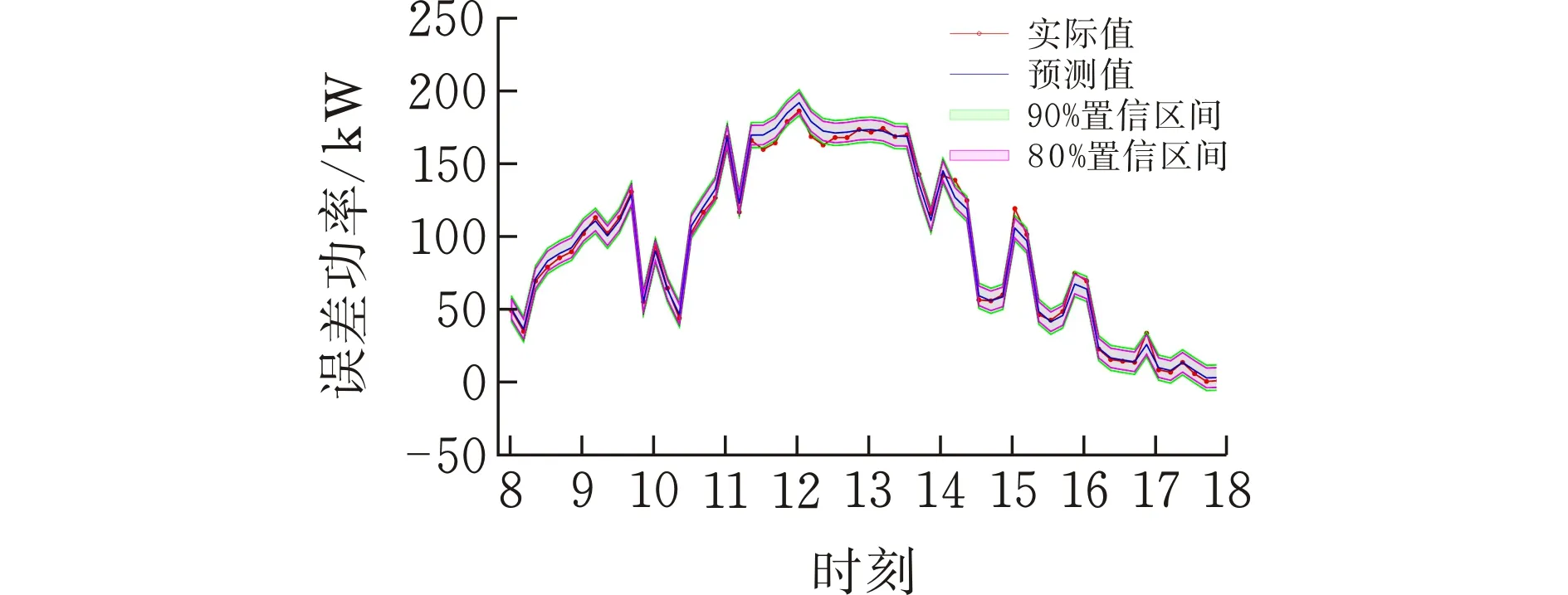
(e) 预测结果之五图 2 不同天气的区间预测

表1 不同模型的预测误差

表2 90%及80%置信区间下不同模型的预测宽度和覆盖率

从图2、表1、表2中可以得到：

1)对于不同的天气情况，特别是图2b和图2d突变天气衰减严重的天气情况和图2c图2e连续变化较大的天气情况，模型3的预测均值能够有效跟随光伏功率的实际值。

2)当置信区间减小时，预测区间的平均宽度也会相应减小。

3)在相同的置信区间条件下，不同的天气状况得到的预测区间宽度。如图2a显示晴天预测区间的平均值则相对较小，而图2b、c、d、e则显示天气变化较大时，预测区间的平均值则相对较大。

4)从表2可以看出，对于几种不同的天气，当采用模型3预测时，得到的预测误差更小、区间覆盖率都能高于设定的置信区间并且具有更小的平均区间宽。

4 总结

本文提出基于PSO-RVM的光伏功率区间预测模型。通过算例分析，得出以下结论：

1)光伏功率的输出具有周期性和随机性，特别是天气因素的变化，对功率的输出有很大的影响。

2)混合核预测相较于单一核预测具有更低的平均绝对误差和均方根误差；在相同的置信区间下，混合核预测的平均宽度更窄。

3)相比于确定性点预测，区间预测能够提供各个时刻的预测范围，方便电力部门的调度，提高电力系统的安全性和稳定性。