融合加权SVD算法的工业机器人运动学标定

班 朝，任国营，王斌锐，陈相君，薛 梓，王 凌

(1.中国计量大学 机电工程学院，浙江 杭州 310018；2.中国计量科学研究院，北京 100029； 3.天津大学 精密测试技术及仪器国家重点实验室，天津 300072)

1 引 言

随着智能制造技术发展的逐渐深入，工业机器人在产品生产制造、加工装配等方面的应用越来越广泛[1]。目前，机械加工产品越来越向着多品种、小批量的方向发展，其加工方式多为离线编程，需要自主调整路径，对机器人绝对定位精度提出了较高要求[2]。根据机器人载荷能力、构型及工作环境的不同，机器人的绝对定位精度最高能达到0.1 mm[3,4]。然而其绝对定位精度往往随着机器人的长期工作和磨损而急剧下降[5]，无法满足精密加工的要求，极大限制了机器人在高精度制造场合的进一步应用。

机器人运动学标定主要包括建模、测量、参数辨识、补偿4个部分，其中测量是标定过程中的关键步骤。在测量过程中，除了测量设备的固定测量误差外，环境或人为因素会引入测量粗差，影响测量坐标系和机器人基坐标系的转换效率，进而对后续运动学参数辨识结果产生影响。

文献[6]使用基于距离误差模型的机器人标定方法，绕过坐标系转换从而避免粗差的影响。文献[7]提出了一种基于误差分布估计的加权最小二乘法进行了机器人手眼标定，该方法虽然考虑了粗差影响，但最小二乘法存在奇异的问题。文献[8]使用四元数结合奇异值分解的方法完成了旋转矩阵和位移矩阵的求解，取得了较好的效果，但该算法较为复杂，计算量大。文献[9]通过相机测量，使用分枝界定的方法来最小化极线约束的目标函数，并没有考虑粗差影响。文献[10]用手眼视觉，提出了一种利用简化的针孔模型与特殊靶板相结合的方案对并联机器人进行了标定，该方法成本低，但精度有待提高。

针对上述问题，本文提出一种加权SVD算法，根据补偿前位置误差设置权重，减少测量粗差的影响，得到了测量坐标系和机器人基坐标系的转换关系，并进一步完成了对IRB2600型机器人的运动学标定。通过仿真和实验，验证了加权SVD算法的稳定性和有效性，经标定后机器人的绝对定位精度得到了提高。

2 机器人模型的建立

2.1 运动学模型

机器人运动学标定的基础是建立一个能有效反映机器人末端位姿误差的误差模型，而建立一个准确有效的运动学模型是建立误差模型的基础[11]。4参数的D-H模型在机器人相邻平行轴处容易发生参数奇异性和突变性的问题。为此，本文采用5参数的MD-H模型[12]，即在D-H模型的基础上增加一个绕y轴方向旋转的转角β。在此，以ABB-IRB2600型工业机器人为研究对象进行运动学分析。在机器人各关节处建立坐标系，根据各个坐标系之间的齐次变换得出相邻连杆之间的关系，从而得到机器人末端执行器的位姿矩阵。IRB2600型机器人MD-H模型连杆坐标系如图1所示。

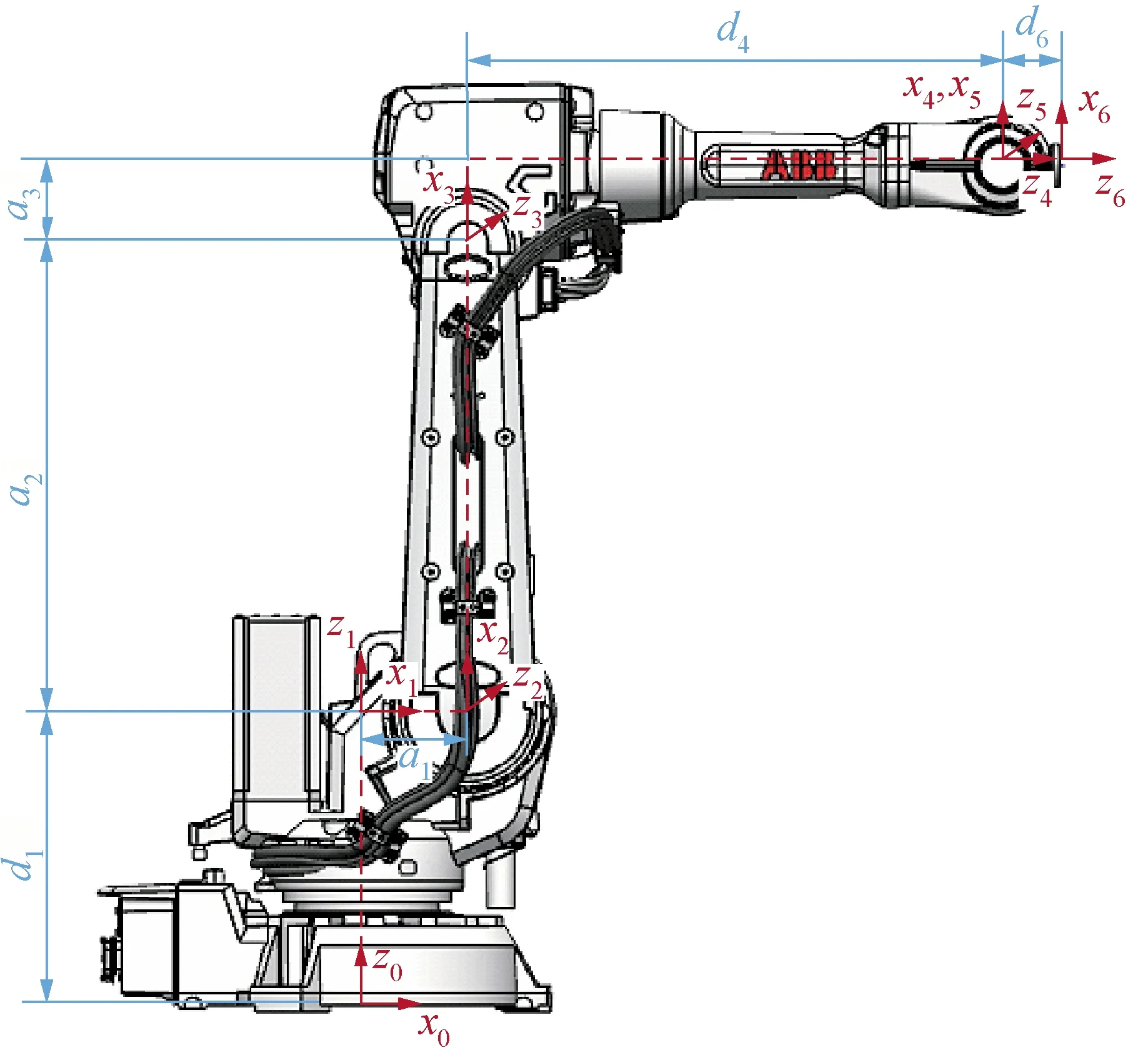
图1 IRB2600型机器人MD-H模型连杆坐标系Fig.1 IRB2600 robot linkage coordinate system based on MD-H model

根据图1中MD-H模型连杆坐标系，机器人相邻连杆间齐次变换矩阵为

i-1Ti=Rot(xi-1,αi-1)Trans(xi-1,ai-1)Rot(zi,θi)Trans(zi,di)Rot(yi,βi)=

(1)

式中：i-1Ti为第i关节坐标系相对于第i-1关节坐标系的齐次变换矩阵；αi-1为连杆扭角；ai-1为连杆长度；θi为关节角；di为偏距；βi为转角；i取1～6。

由机器人正运动学方程可得末端位姿矩阵：

(2)

由于IRB2600型机器人第2轴和第3轴平行，只需在第2轴处增加一个绕y2轴转动的转角β2，使z2轴变换到z3轴，从而避免D-H模型的缺陷(其他非平行轴转角β参数不存在)。得到机器人运动学参数见表1，表中括号内数值表示此参数的初值。

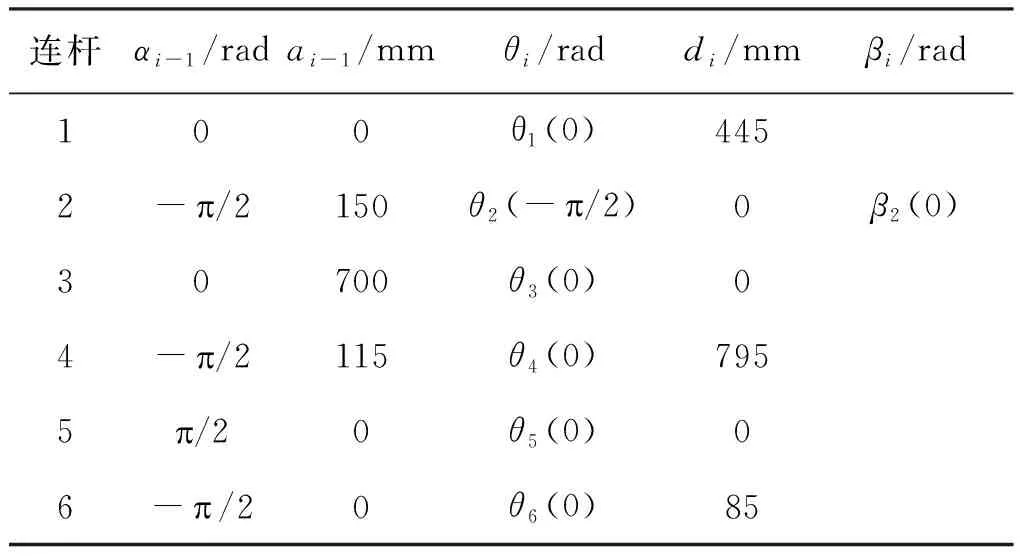
表1 IRB2600型机器人运动学参数Tab.1 Kinematics parameters of IRB2600 robot

2.2 误差模型

在影响机器人绝对定位精度的所有因素中，研究表明因几何参数变化而引起的误差占总误差的80%以上[13,14]。为方便建立机器人误差模型，在此忽略齿轮间隙、连杆柔性、环境温度等其他非几何参数误差，仅考虑描述连杆的几何参数误差。

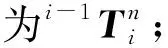
对式(1)求全微分得：

(3)

为简化式(3)，需将di-1Ti表示成与i-1Ti的函数关系，假设：

(4)

式中：Dα，Da，Dθ，Dd，Dβ为系数矩阵，将i-1Ti取逆移至等号左边，可得各系数矩阵值。

联立式(3)、式(4)可得：

di-1Ti=i-1Ti(DαΔαi-1+DaΔai-1+

DθΔθi+DdΔdi+DβΔβi)

(5)

由坐标系间的微分运动得：

di-1Ti=i-1TiΔi

(6)

式中：Δi为基于第i-1关节坐标系，第i关节微分变换矩阵，满足式(7)。

(7)

式中：dxi、dyi、dzi为微分平移量；δxi、δyi、δzi为微分旋转量。

联立式(5)、式(6)得：

(8)

将式(8)用微分运动列矢量Di来表示微分变换，同时设第i关节的误差系数矩阵为Gi，运动学参数误差列矢量为Ei，则：

Di=GiEi

(9)

式(9)建立了关节i的微分误差模型，而机器人末端位姿误差是由机器人各关节误差叠加而成，又因为在实际测量中得到的是机器人末端位姿，所以需将机器人各关节误差变换到机器人末端。

根据机器人微分变换原理[15]，令6ji为第i关节坐标系到末端坐标系的微分误差变换矩阵：

(10)

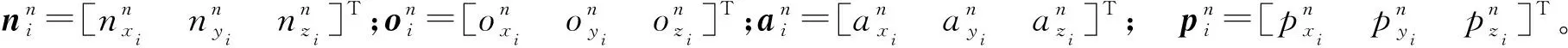
因此，机器人误差模型描述为

(11)

式中：Dn为变换后名义微分运动列矢量；J为雅克比矩阵；E为各连杆参数误差列矢量集合。

3 加权SVD算法

激光跟踪仪通常被选用作为测量设备[16]。在激光跟踪仪测量过程中，实际测量得到的坐标是基于自身坐标系的坐标值，需要将其转换到机器人基坐标系。本文采用SVD算法进行坐标系的旋转平移变换，其数学模型为：

(12)

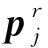
为求解式(12)的极小值，对其进行求偏导：

(13)

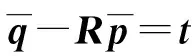
(14)

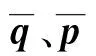
(15)

将式(14)代入式(12)消去t化简得：

(16)

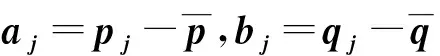
将式(16)拓展、变换得：

=arg max(tr(RAWBT))

(17)

式中：A=[a1a2…am]；B=[b1b2…bm]；W为权重系数对角矩阵。

对矩阵AWBT进行奇异值分解得：

AWBT=UΛVT

(18)

式中：U为左奇异矩阵；VT为右奇异矩阵的转置；Λ为对角矩阵。

联立式(17)、式(18)得：

R=arg max(tr(RUΛVT)) =arg max(tr(ΛVTRU))

(19)

式中：V、R、U均为正交矩阵，当VTRU=I时，R取最大值。

此时：

R=VUT

(20)

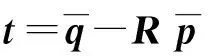
(21)

通过R、t便可求出转换后基于机器人基坐标系的点集合，从而完成坐标系的转换。但在标定过程中，一般默认W=I，即各测量数据的权重均为1。但在激光跟踪仪测量过程中，激光本身易受环境(温度、湿度、压强等)影响，从而影响测量精度；同时一些人为因素影响也会对测量造成较大误差，例如：人经过正在测量的激光跟踪仪时带来的地基震动和空气扰动造成的误差等。此时若采用等权重的计算方法来进行坐标系转换，会使SVD算法稳定性下降。因此，本文在算法中重新分配权重系数。

首先，根据上述算法，设置W=I，等权重进行坐标系转换，对每个测量点求取位置误差：

(22)

此时，位置误差的平均值为：

(23)

再而，根据各测量点位置误差大小重新分配权重系数，使误差较大的测量点权重降低，从而增加SVD算法的稳定性。在此，取权重函数：

(24)

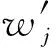
(25)

最后，根据式(25)对修正后的权重系数矩阵W′权重均衡化，将结果代入SVD算法中得修正后的旋转矩阵和平移矩阵。

4 机器人误差辨识算法与补偿方法

4.1 误差辨识算法

Levenberg-Marquart(L-M)算法是梯度下降法和Gauss-Newton法的结合，目的在于解决Hessian构造矩阵的非正定问题和奇异问题[17]。相较于最小二乘法，L-M算法增加了阻尼因子λk用于调节算法特性，使其具有Gauss-Newton法的快速收敛特性和梯度下降法的全局特性。其中，当λk值很大时，Hessian矩阵非对角线元素相对于对角线元素而言不再重要，L-M算法退化为梯度下降法；当λk值很小时，L-M算法退化为Gauss-Newton法，在接近正确解时算法能快速收敛。其迭代式为：

(26)

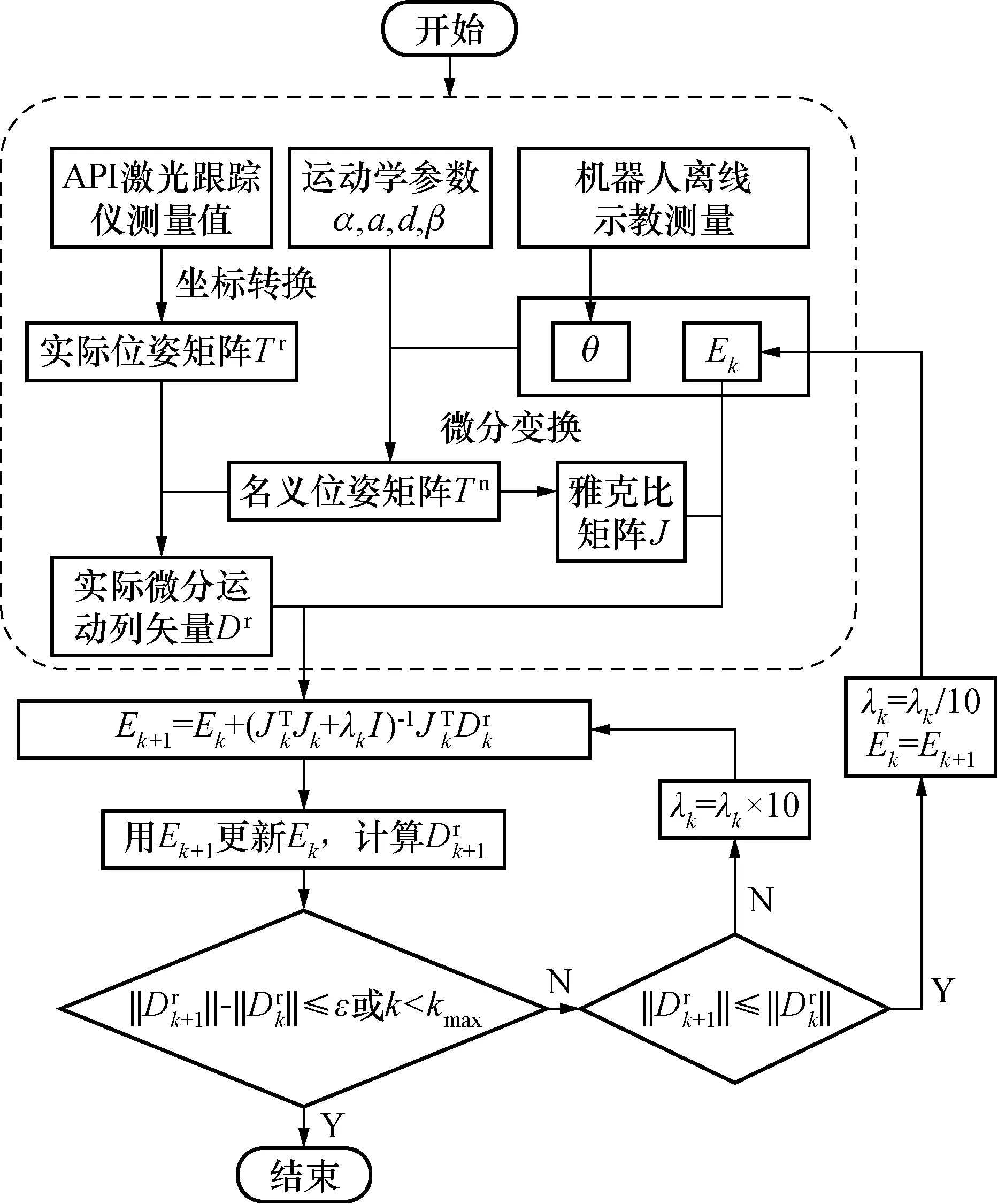
图2 L-M算法运动学误差参数辨识流程Fig.2 Kinematic error parameter identification process of L-M algorithm

4.2 误差补偿方法

工业机器人误差补偿就是基于运动学模型辨识出的误差参数对机器人的结构参数进行补偿的过程[18]。机器人名义位姿Tn(αi-1,ai-1,θi,di)经过补偿后得到实际位姿Tr(αi-1+Δαi-1,ai-1+Δai-1,θi+Δθi,di+Δdi)，由于E的取值在一个很小的范围内，为使机器人达到名义位姿，可以在机器人进行下一次位姿测量时通过修改机器人底层模型相关参数，将指令位姿修改为Tn(αi-1-Δαi-1,ai-1-Δai-1,θi-Δθi,di-Δdi)的方法实现。但大多数机器人生产厂家不开放底层控制模块，故无法直接验证误差参数辨识结果的准确性。因此，本文通过将补偿后得到的实际位姿和激光跟踪仪测量得到的实际位姿进行比较，间接验证辨识结果的准确性。

5 仿真与实验结果分析

5.1 仿真方案设计

为验证改进后SVD算法的有效性和稳定性，在Matlab上对算法进行仿真测试，具体分为以下3个步骤。

(1) 任意选择50个空间坐标构成点集合P，设定旋转矩阵R和平移矩阵t，得到坐标转换后点集合Q，作为标准值。

(2) 在点集合P中各点x、y、z方向添加0～0.02 mm随机误差，模拟固定测量误差；任选2、4、6、8、10、12、14、16个点，添加0～0.2 mm、0～0.4 mm、0～0.6 mm、0～0.8 mm、0～1 mm 5个范围的粗差，模拟由环境或人为因素而引入的测量粗差，得到含有粗差的点集合P1。

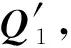
5.2 仿真结果分析

为了更直观比较两算法性能差异，通过将SVD算法计算得到的平均绝对误差值与加权SVD算法得到的平均绝对误差值相减，得到平均绝对误差差值。两算法性能比较如图3所示。

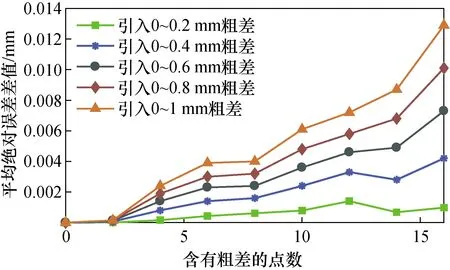
图3 SVD算法和加权SVD算法性能比较Fig.3 Performance comparison of SVD algorithm and weighted SVD algorithm

由图3可见，随着粗差点数和范围的增加，平均绝对误差差值会随之变大。由此可知，与SVD算法相比，本文算法稳定性更优，能够降低环境或人为因素引入的测量粗差对坐标系转换的影响。

5.3 实验方案设计

本文在ABB-IRB2600型机器人末端安装了一个合作靶标，用来固定靶球。测量装置选用API公司生产的激光跟踪仪，测量精度为10 μm，通过末端靶球可以准确获取机器人末端位置数据。因为机器人各关节间为强耦合关系，当机器人位置精度提高时姿态精度也会提高，所以在实验中不考虑机器人姿态影响。

在实验开始前，为避免机器人标定陷入局部最优，先利用ABB自带的Robot Studio软件进行离线编程，选择边长为800 mm的立方体测量空间，均匀获取空间内50个点坐标作为机器人名义位置坐标。再通过示教器离线示教控制机器人依次运动至这50个点坐标位置，并在每个点停留5 s供激光跟踪仪进行数据采集。机器人标定实验现场布局如图4所示。

图4 机器人标定实验现场布局Fig.4 Layout of robot calibration experiment site

5.4 实验结果分析

当激光跟踪仪测量得到50个点坐标数据后，由于实际测量得到的是末端靶球中心点位置坐标，测量点相对于机器人末端坐标系存在一个平移变换，即式(2)中6Ttool，首先需要先进行工具坐标系标定。在此，通过机器人正运动学和两点之间的距离公式，结合最小二乘法计算出机器人末端坐标系沿x，y，z方向平移的最优值Ptool=[1.059 9,0.540 9,34.7249]T，单位mm。根据式(2)机器人正运动学可得基于机器人基坐标系的名义位姿。

其次，进行测量坐标系和机器人基坐标系的转换。将Spatial Analyzer(SA)三维测量分析软件进行坐标系转换的求解结果作为参照对比。分别经3种算法拟合求解后得到的补偿前各测量点位置误差如图5所示，误差统计如表2所示。

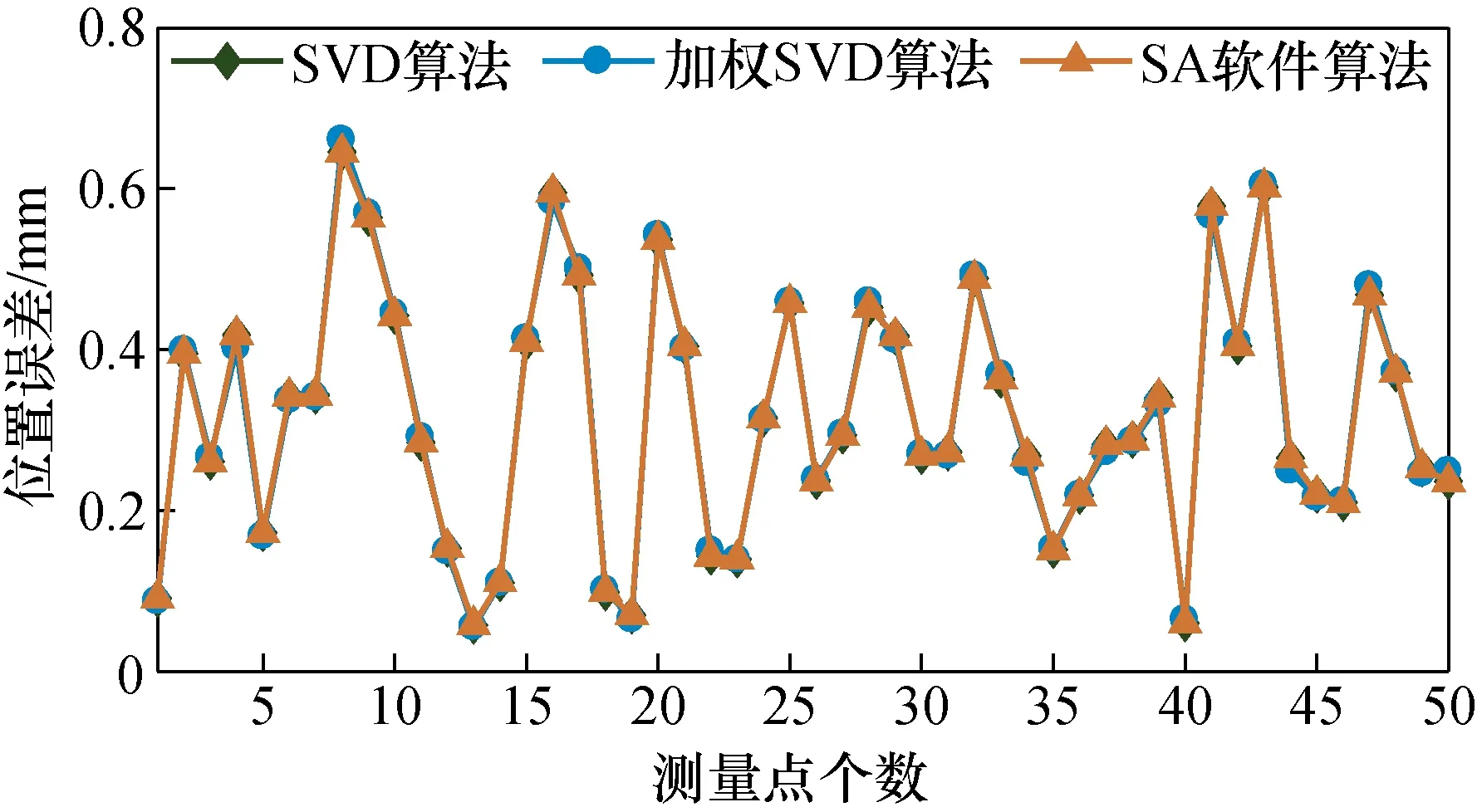
图5 3种算法计算得到的位置误差对比Fig.5 Comparison of the position error calculated by 3 algorithms

表2 3种算法计算得到的位置误差统计Tab.2 Statistics of the position error calculated by 3 algorithms mm

从图5中可以看出各算法均起到了很好的拟合效果。其中，SVD算法和SA软件中的算法计算得到的位置误差基本一致，表2中的位置误差统计同样验证了这一点，说明这两种算法均没有改变各测量点的权重。而使用加权SVD算法后计算得到的MAE要小于其他两算法计算结果，但差别不大，这主要是由于实验中测量粗差引入量很小所致。本文加权SVD算法得到50个点坐标转换前后可视化分布如图6所示。

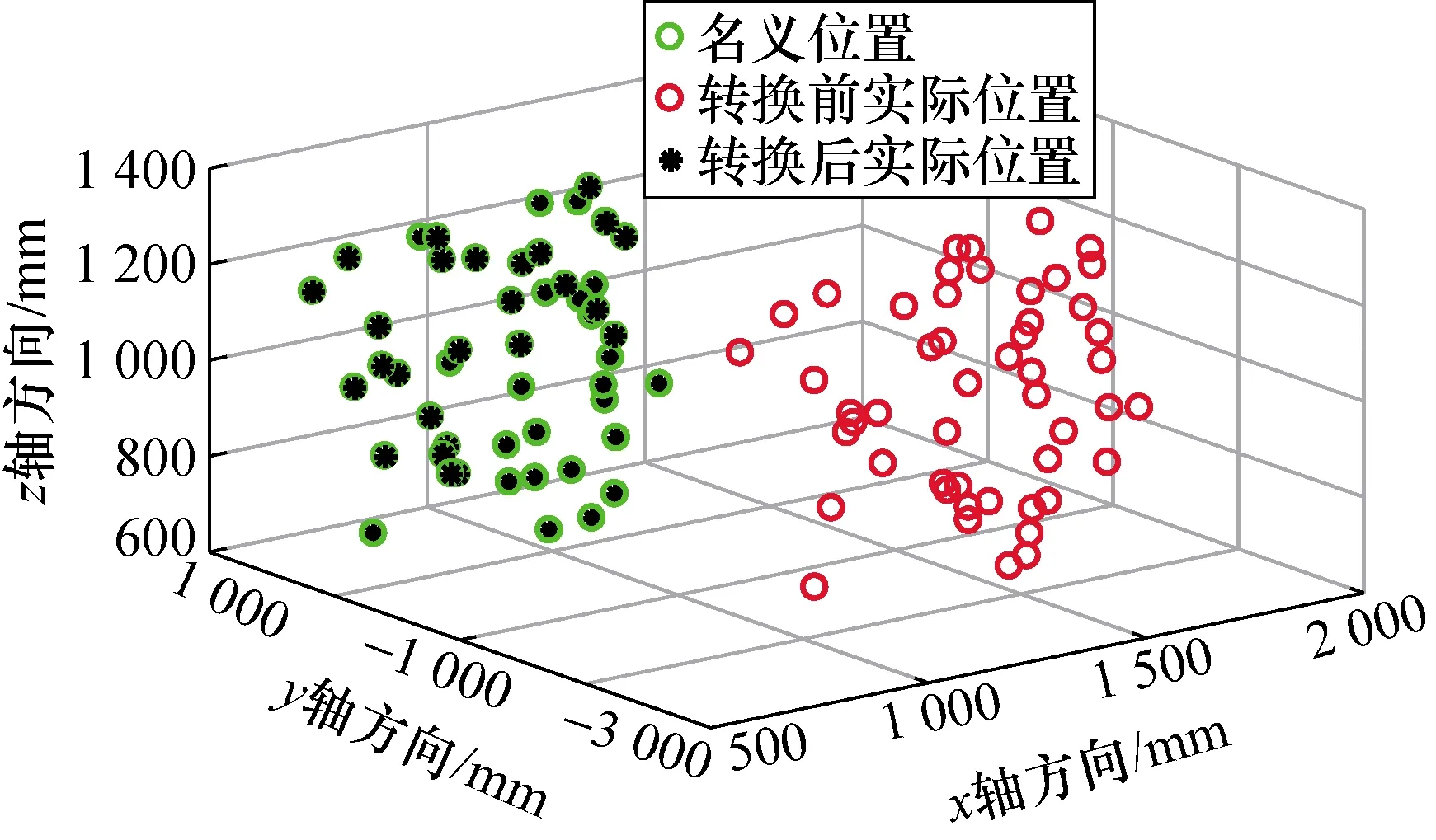
图6 50个点坐标转换前后的可视化分布Fig.6 Visual distribution before and after coordinate transformation of 50 points

最后，进行机器人的运动学参数辨识和补偿。将实验中机器人50组关节角度数据和测量得到的实际位置数据代入L-M算法运动学参数误差辨识流程中，其中算法阻尼因子λ初值取0.01，阈值ε取10-5，最大迭代次数kmax=50。机器人第六轴关节角对机器人末端位置无影响，经辨识后参数为冗余参数不参与辨识，误差参数辨识结果(保留小数点后6位)如表3所示。

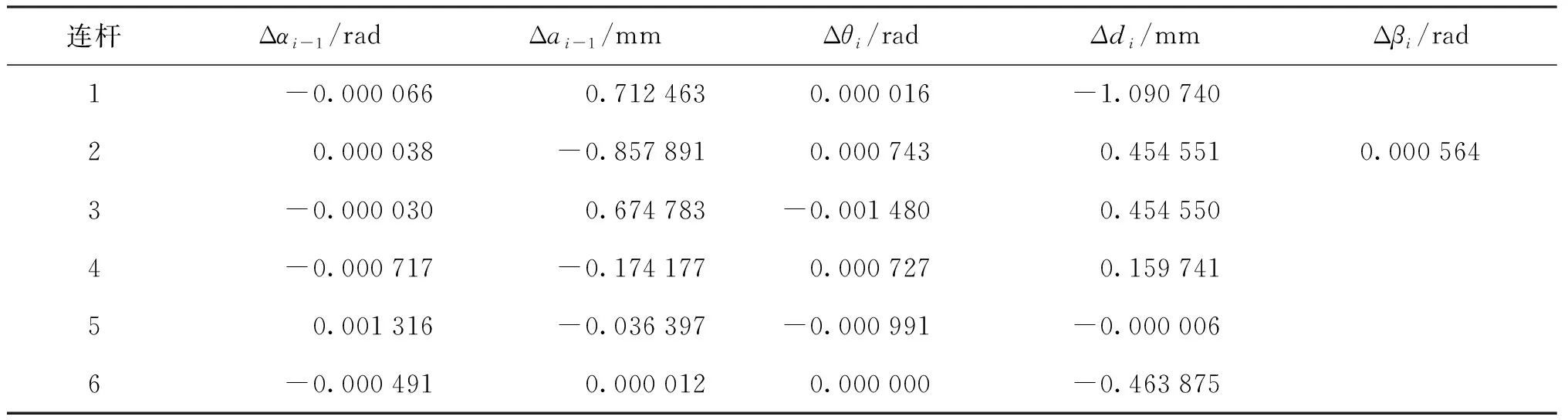
表3 融合加权SVD算法的误差参数辨识结果Tab.3 The result of error parameter identification fusing weighted SVD improved algorithm

机器人运动学标定的主要目的是提高机器人绝对定位精度，为了验证ABB-IRB2600型机器人的绝对定位精度是否因误差补偿后有所提高，本文以平均绝对误差MAE和均方根误差RMSE作为机器人绝对定位精度的评价指标。

图7为补偿前后机器人位置误差对比情况，从中可以看出，50个测量点中的45个测量点均得到了很好的补偿效果。表4中的误差统计结果表明：补偿后机器人平均绝对误差降低了65.10%，均方根误差降低了65.85%，经过运动学标定后机器人绝对定位精度得到了有效提高。

表4 补偿前后机器人位置误差统计Tab.4 Statistics of robot position error before and after compensation mm

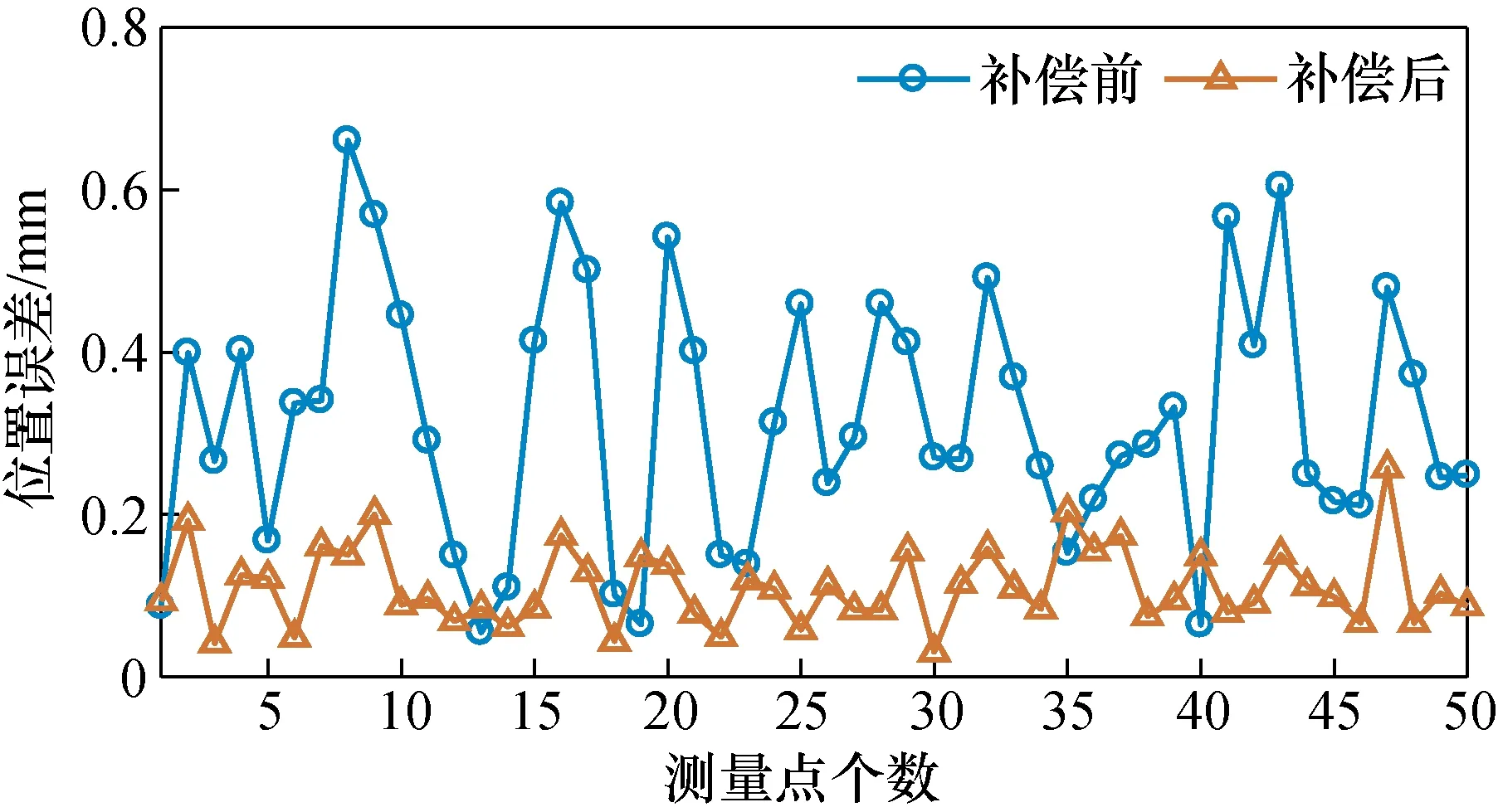
图7 补偿前后机器人位置误差对比Fig.7 Comparison of robot position error before and after compensation

由于实验室环境为恒温恒压的理想环境，人为因素影响小，从而引入的测量粗差很小；使用辨识前的位置误差近似测量粗差分配权值，本身存在一定误差；SVD算法中用到了机器人名义坐标，会使补偿前位置误差结果偏好。综上，本文改进算法的实验效果并不明显。但在实际应用中，面对复杂环境的影响，本文算法在精度要求高的机器人标定中效果将更为明显。

6 结 论

本文采用API激光跟踪仪作为机器人末端位置测量设备，结合MD-H模型和L-M辨识算法，使用加权SVD算法对测量坐标系和机器人坐标系进行了转换，解决了因环境或人为因素引入的测量粗差对坐标系转换效率存在较大影响的问题，完成了ABB-IRB2600型工业机器人的运动学标定。仿真和实验结果表明：随着测量粗差点数和范围的增加，与SVD算法相比，本文提出的加权SVD算法具有更好的稳定性；将其应用于机器人运动学标定，标定后机器人的绝对定位精度得到了明显提高。