分段函数要求高 七种题型要记牢

■樊文联

分段函数是在不同定义区间上具有不同的解析式,是一类重要的函数。在处理分段函数问题时,应对不同的区间进行分类讨论,然后整合,这恰好是分类讨论的一种体现。

题型1:求函数的值

点评

已知分段函数解析式求函数值的方法:①确定要求值的自变量属于哪个区间;②代入该段的解析式求值。当出现f[f(x0)]的形式时,应从内到外依次求值。

题型2:求函数的值域

例2函数f(x)=的值域是()。

A.R B.[0,2]∪{3}

C.[0,+∞) D.[0,3]

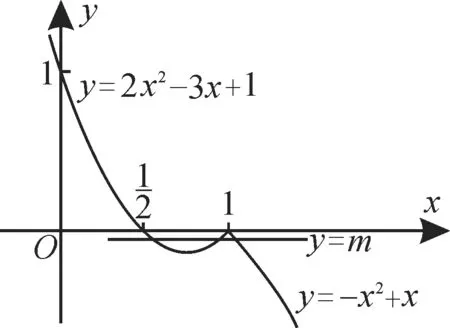
解:当0≤x≤1 时,0≤2x≤2,即0≤f(x)≤2;当1

点评

求分段函数的值域,就是求各段函数值域的并集。

题型3:求参数的值

例3已知分段函数f(x)=若f(a)=3,则实数a的值为_____。

解:根据题意可分段求解。①当a≤-2时,由f(a)=a+4=3,可得a=-1>-2,不合题意,舍去。②当-2

点评

已知分段函数的值求参数值的三个步骤:先对参数的取值范围进行分类讨论;然后代入不同的解析式,通过解方程求出参数的值;检验所求的值是否属于所讨论的区间。

题型4:求参数的取值范围

例4已知分段函数f(x)=在区间 [-1,m]上的最大值是2,则实数m的取值范围是_____。

解:当x≤0 时,f(x)=3-x-1 是减函数,所以3-x-1≤2,解得-1≤x≤0。当x>0时,f(x)=是增函数,所以≤2,解得0

点评

分段函数的求值或求取值范围问题,要注意每段都应考虑是否满足条件。

题型5:新定义问题

例5对于实数a和b,定义运算“*”:设函数f(x)=(2x-1)*x,且关于x的方程f(x)=m(m∈R)恰有三个互不相等的实根,则实数m的取值范围是_____。

解:由新定义得函数f(x)=(2x-1)*作出分段函数f(x)的图像,如图1所示。

图1

由函数的图像与性质可知,当x=时,y=2x2-3x+1取得最小值为-。函数y=-x2+x在(1,+∞)上单调递减,则y=-x2+x<0。因为y=f(x)=m(m∈R)恰有三个互不相等的实根,所以-

点评

本题是以新定义的形式来考查函数的图像与性质的。题中要求方程的三个不相等的实根,只需求出对应函数图像的三个交点即可。作图、识图、用图是解答本题的关键。

题型6:不等式问题

点评

题中函数f(x)的定义域为[-1,0)∪(0,1]。-x与x的大小关系不确定,因此需要分类讨论。

题型7:单调性问题

例7已知分段函数f(x)=是R 上的增函数,则实数a的取值范围为()。

A.(1,+∞) B.(1,8)

C.(4,8) D.[4,8)

点评

解决分段函数的单调性问题,要抓住对自变量所在区间的讨论,在保证各段上同增(减)时,要注意上、下段间端点值的大小关系。

感悟与提高

若函数f(x)在闭区间[-1,2]上的图像如图2所示,则此函数的解析式为________。

提示:由图可知,当-1≤x<0 时,f(x)=x+1;当0≤x≤2 时,f(x)=。所 以 函 数

图2