一种新的Bernstein-Stancu算子在移动区间上的逼近性质

王凤凤，虞旦盛*，卢诚波

（1.杭州师范大学理学院，浙江杭州 311121；2.丽水学院工学院，浙江丽水 323000）

0 引言和概念

1968年，Stancu[1]引入了所谓的Bernstein-Stancu多项式。设f∈C［0，1］，相应的Bernstein-Stancu算子定义为：

2010年，Gadjiev和Ghorbanalizadeh[2]引入了以下具有移动节点的一般化Bernstein-Stancu算子：

其中

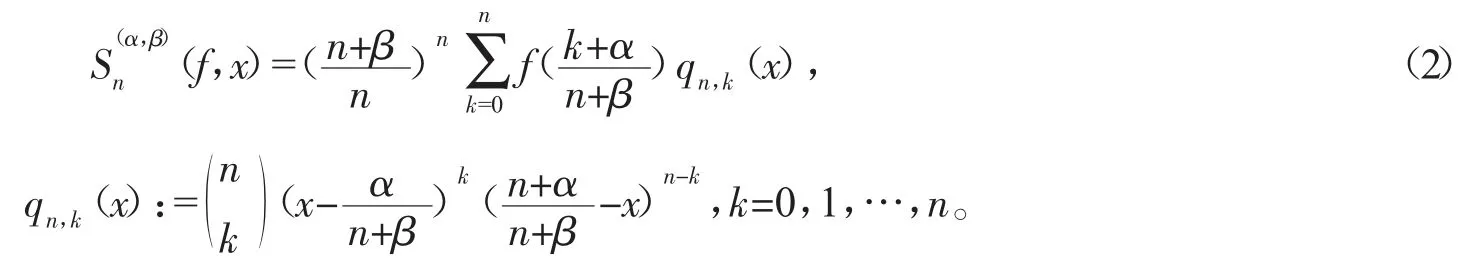
定理1 设0≤λ≤1为固定常数，则对任何f∈C（An），存在一个仅依赖于λ、α和β的正常数C，使得

定理2 设f∈C（An），0＜θ＜2，则有

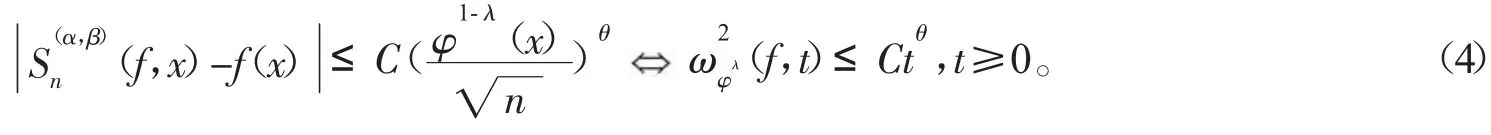
如果f（x）具有二阶连续导数，即f（x）∈C2（An），我们有下面的Voronovskaja型估计：

定理3 对任何f∈C2（An），存在一个仅依赖于λ、α和β的正常数C，使得

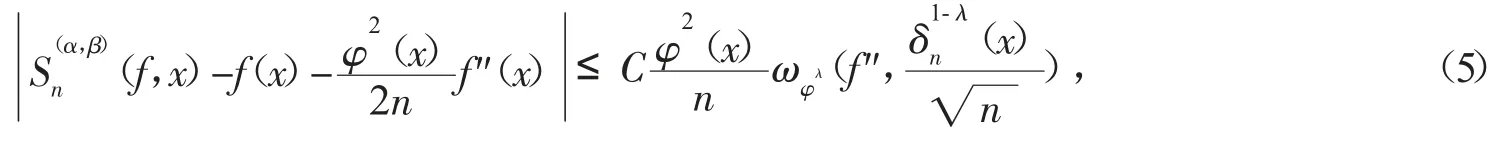
注 本文中，C表示一个正的绝对常数，或依赖于某些参数但不依赖于f、x和n的正的常数，它们的值在不同的情况下可能不同。本文中A～B指的是存在两个正常数C1和C2，使得C1A≤B≤C2A。

1 引理及其证明

为了证明上述定理，我们首先给出几个引理。

引理1下列等式成立：

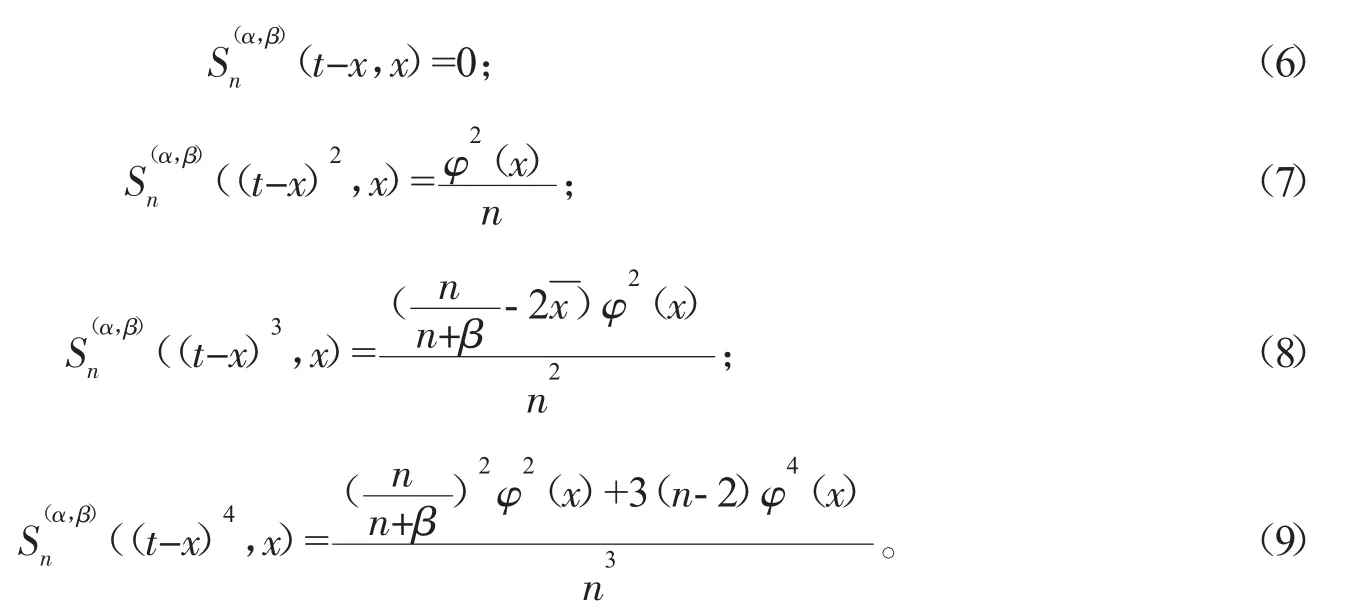
证明 通过简单的计算可得：

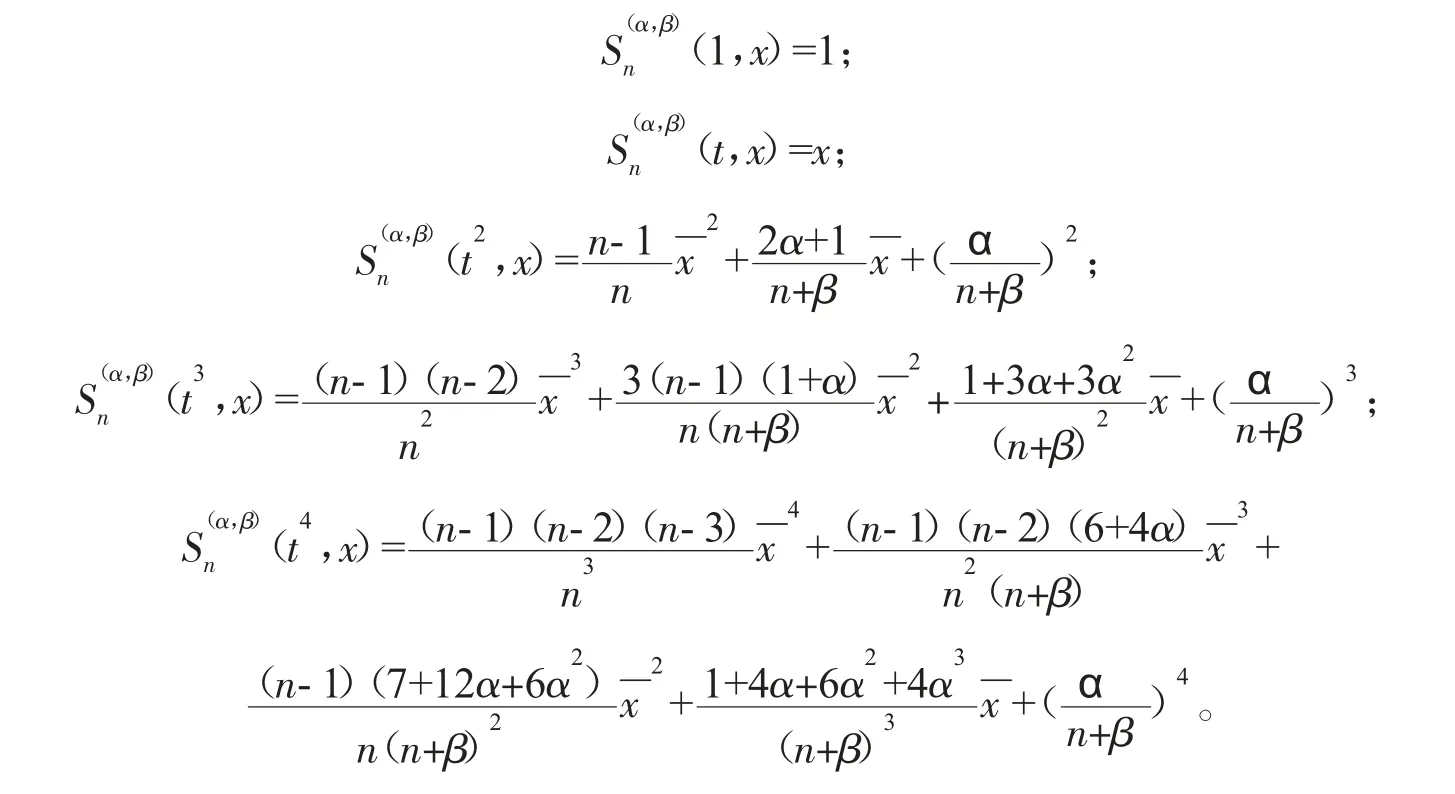
因此，

引理2[13]设（x）为［a，b］上不恒等于0的函数，且2为上凸的，则对所有x∈［a，b］，h＞0满足x±h∈［a，b］，下式成立：

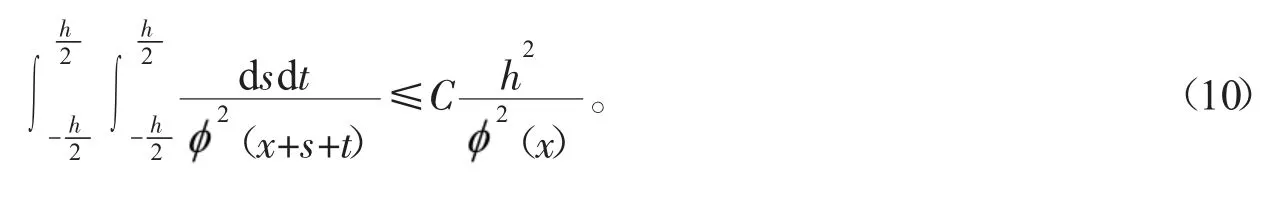
引理3对任何t，，0≤λ≤1，下式成立：

证明 通过直接计算可得

引理4设f∈C（An），则下式成立：

证明 通过简单计算可得

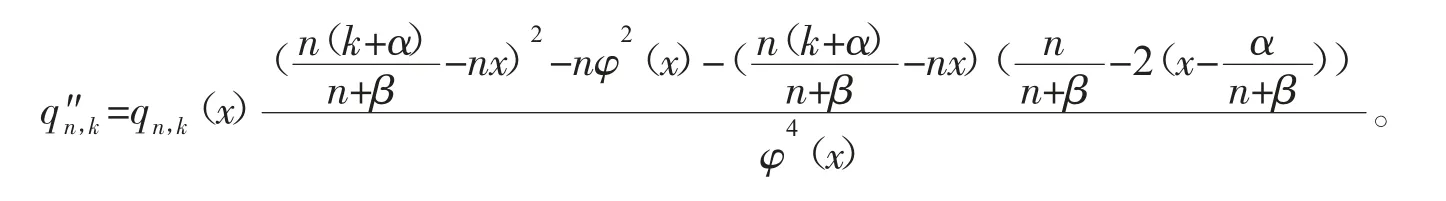
故有

利用Cauchy-Schwarz不等式，有

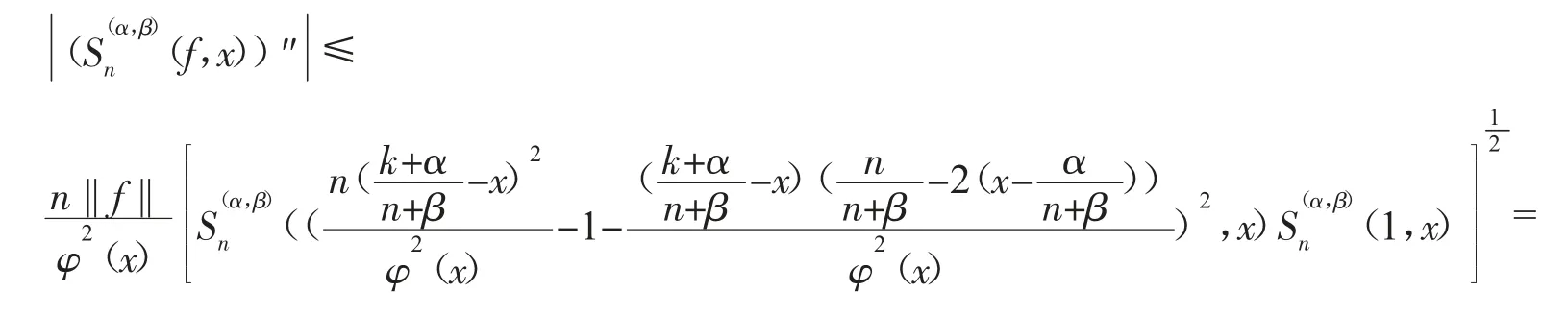
从而

引理4得证。

证明 记

直接计算可得

下面开始证明式（13）。对任意的s=t+τ（x-t），τ∈An，利用φ2λ（x）的凸性，知

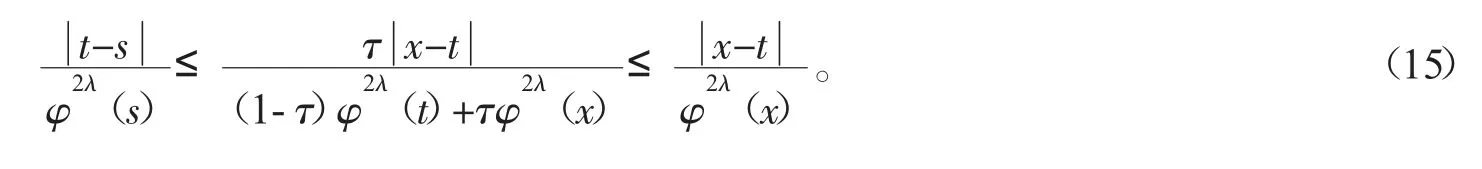
利用式（15）和Taylor公式：

得

因此，

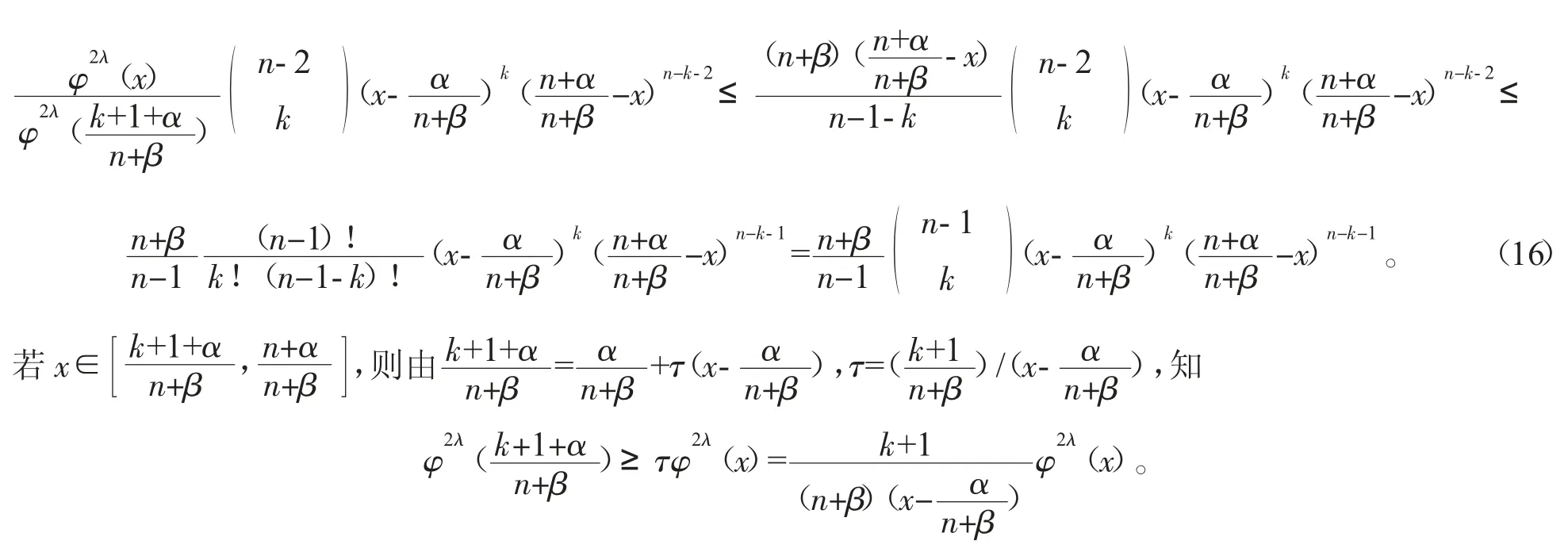
因此，

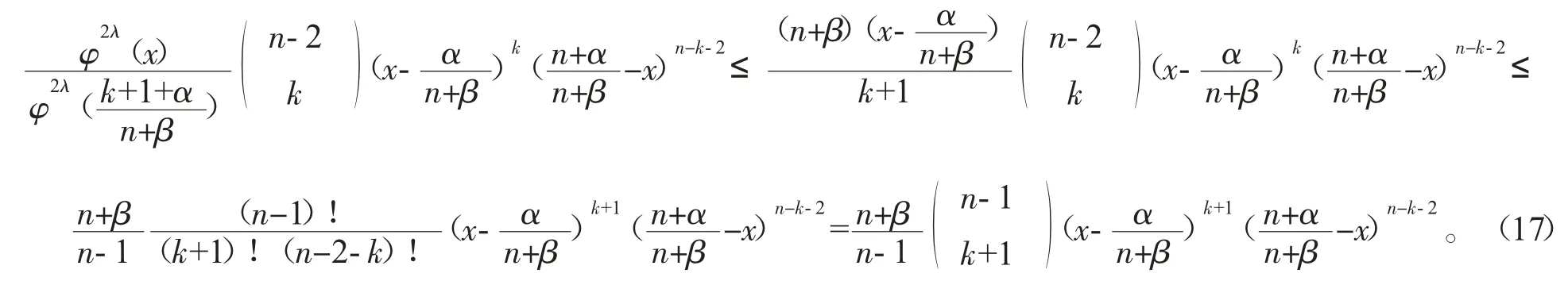
2 定理的证明

定理1的证明 显然

定义

根据式（18）和式（19），我们有

利用Taylor展开式

以及下列不等式（见文［6］）：

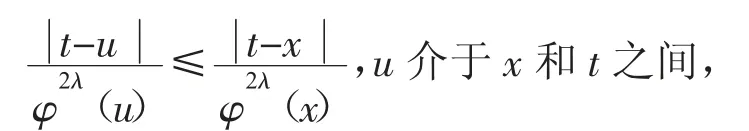
得

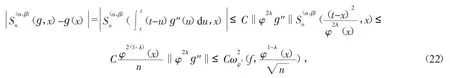
其中上述的最后一个式子用到了式（20）。

结合式（21）和式（22），定理1得证。

定理2的证明 充分性的证明由定理1可以直接推得。下面我们证明必要性。设x，h∈An，使得x±h∈An。显然，

下面分别估计上式右边的两项的值。利用φ2（1-λ）（x）的凸性可知，

通过定理的假设，我们可以得到

由引理4和引理5，可得

现在利用引理2，就有

用hφλ（x）代替h，

于是

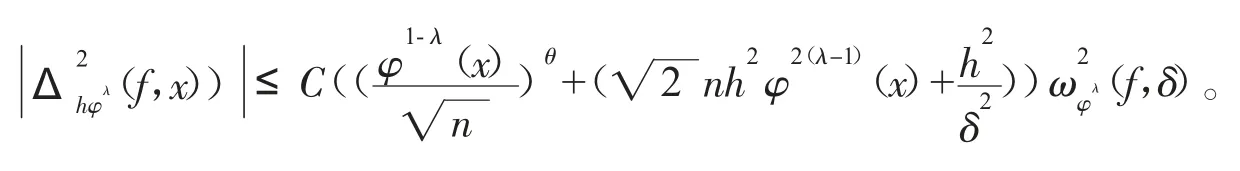
选择n使得

这样就有

对上式关于h在0＜h≤t取上确界得到，0＜t≤δ。

利用著名的Berens和Lorentz引理[15]，即知必要性成立。

定理3的证明 对任何f∈C（An），定义K-泛函：

利用引理1和Taylor展开式：

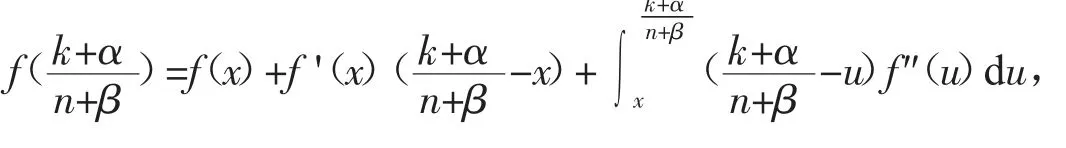
可以得到

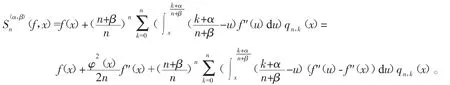
从而，

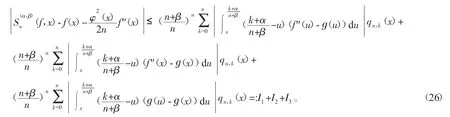
利用式（7）和式（23），就有

类似地

我们分下面两种情形来估计I3。

情形1。此时，有及，…，因此，

由Cauchy不等式及式（7）和式（9），得

利用式（29），我们继续估计I3，

在最后一个不等式中我们利用了式（24）和式（25）。

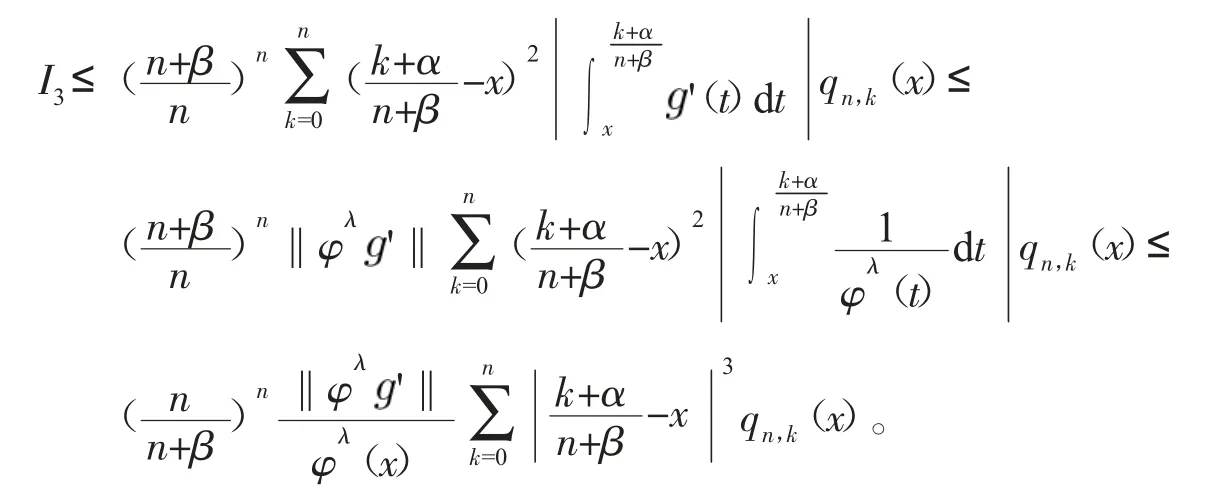
利用式（29）和δn（x）～φ（x），推得

结合式（26）（27）（28）（30）和（31），定理3得证。