基于二次分析的双机器人避碰方法研究

姚世选,刘永健,崔泽,刘小臣

(1.大连外国语大学 软件学院，辽宁 大连 116044；2.大连交通大学 机械工程学院，辽宁 大连 116028)*

工业机器人的出现，大大解放了人类的体力劳动，各国对机器人研究的步伐从未停止，机器人的出现提高了生产效率，把人们从单一重复的危险工作中解放了出来，填补了生产力的不足[1].随着减速器和运动控制器等机器人相关技术的发展，机器人技术逐渐满足难度和精度日益提高的复杂运动作业要求；计算机硬件及网络技术的发展，使机器人技术所需的高度复杂计算能力和协同操作能力成为现实.随着机械工程、计算机技术、电子通讯、智能控制等学科领域的快速发展，机器人技术已经从理论实验阶段走向了实际应用阶段[2].但是随着机器人在各行业领域应用的不断深入，单机器人系统本身存在的一些弊端逐渐显露出来，传统单机器人系统的发展正面临着巨大挑战，由于其本身结构布局、处理效力、响应速度等因素的限制，很难满足不断增长的实际生产需要.因此对多机器人系统的研究逐步成为近些年来各国研究追捧的热点，多机器人系统比单机器人系统有更多的优点[3].例如，多机器人系统比单机器人系统拥有更好的时间和空间互补性，能够弥补单机器人系统由于自身结构或功率局限性造成的加工性能低下的问题[4]；多机器人系统能更好的适应不断变换的工作环境，更容易满足日益提高的加工任务难度，更高的数据冗余性使多机器人系统更加的稳定高效[5]；另外，简单多机器人系统的研发生产成本往往要比高精度复杂的单机器人系统要低得多[6].多机器人系统可以弥补单机器人系统中存在的短板不足，可以胜任许多单机器人系统不能完成或者完成效果不理想的任务.

目前已经有很多关于多机器人系统的研究，其中各机器人间的协调避碰问题是多机器人系统研究中重点和难点问题.多机器人协调避碰方法主要有人工势场法[7]、基于市场经济的方法[8]、基于神经网络算法的避碰方法[9]等.本文以双机器人系统为研究对象，提出一种针对二维加工任务的协调避碰研究方法，该方法同样适用于多机器人系统.首先将单机器人加工任务用栅格法[10]进行离散化表达，建立碰撞分析数学模型，对加工任务进行二次分析，规划出双机器人系统的协同加工方法.

1 任务表达

1.1 加工任务的栅格法表示

栅格法表示就是将加工任务和环境使用若干个二维小矩形进行表示，同时说明每个小矩形表达的信息[11].首先将加工平面、机器人末端执行器和刀具用栅格进行表示.当加工任务形状不规则时将其边缘拓展为一整个栅格，并且将机器人末端执行器边缘转化形成一个个小矩形栅格，如图1所示，这样就可以将加工任务和环境使用栅格法进行离散化表达.

图1 栅格表示法

其次对每个小栅格所表达的信息进行说明.计算出加工中每个小栅格被机器人末端执行器遮挡的时间，以设色图的形式直观地表示出来，这样就可以很清楚的知道加工时末端执行器的运行情况，了解平面上哪些位置的重复遮挡现象严重，造成了加工时间和效率的浪费.

1.2 栅格信息表达

图2 点P的遮挡示意图

设s为连续加工时对点P(i,j)造成遮挡的加工路径，v(i,j)为机器人末端执行器加工速度，则机器人末端执行器对加工平面上任意一点点P的遮挡时间TP为：

通过上述方法，即可将整个加工平面上每个点对应小栅格的加工遮挡时间计算出来.整个加工平面可以看成由m×n个小栅格组成，将加工平面视为一个m×n阶的矩阵，加工平面上每个小栅格的遮挡时间转化成矩阵中的对应元素，即可以通过矩阵表示出整个加工平面的加工遮挡情况，根据栅格化的加工平面建立描述矩阵如下：

基于上述方式，即可将整个加工平面使用栅格法进行离散化，之后通过对每个栅格被机器人末端执行器遮挡时间的计算描述，用设色图将整个加工平面上各点的遮挡时间清晰地表示出来.矩阵中m和n分别表示加工平面长和宽经栅格法离散化的栅格数量.

例如针对如图3所示的PCB雕刻任务，首先将加工平面使用栅格法进行离散化表达，之后计算每个栅格被机器人末端执行器遮挡的时间，并以设色图的形式进行直观地显示，图3中下层为栅格化处理后的加工任务，上层为加工平面上每点遮挡时间的设色图.从图中可以看出有很多区域的重复遮挡加工现象严重，即说明该区域造成了效率能耗资源的浪费，同时若对该区域进行协同加工，则出现碰撞的风险也较高，协同加工系统的稳定性低.

图3 PCB雕刻任务的遮挡时间设色图

2 避碰策略研究

2.1 碰撞分析

已知，实际单机器人加工时，每一个时刻对应一个加工任务栅格.将单机器人加工任务经栅格法离散化之后的小栅格标记为任务点{p1，p2，p3，…，pn}，则任务点{p1，p2，p3，…，pn}与加工时刻一一对应，则可以通过对加工任务{p1，p2，p3，…，pn}进行二次分析，规划得到双机器人系统的避碰协同加工方法.

针对图4所示某一临近双矩形图案平面加工任务，AB、CD(EF)、GH长度均为71 mm， BC、AD、EH、FG长度均为31 mm，两矩形相距5 mm.单机器人加工时，由点A开始，依次经点B-C-D回到点A，之后机器人跳转至点E，再经由点F-G-H回到点E，最终完成加工.设机器人末端执行器半径为8 mm，加工速度为v=1 mm/s，且暂不考虑机器人从点A至点E重定位的动作时间.

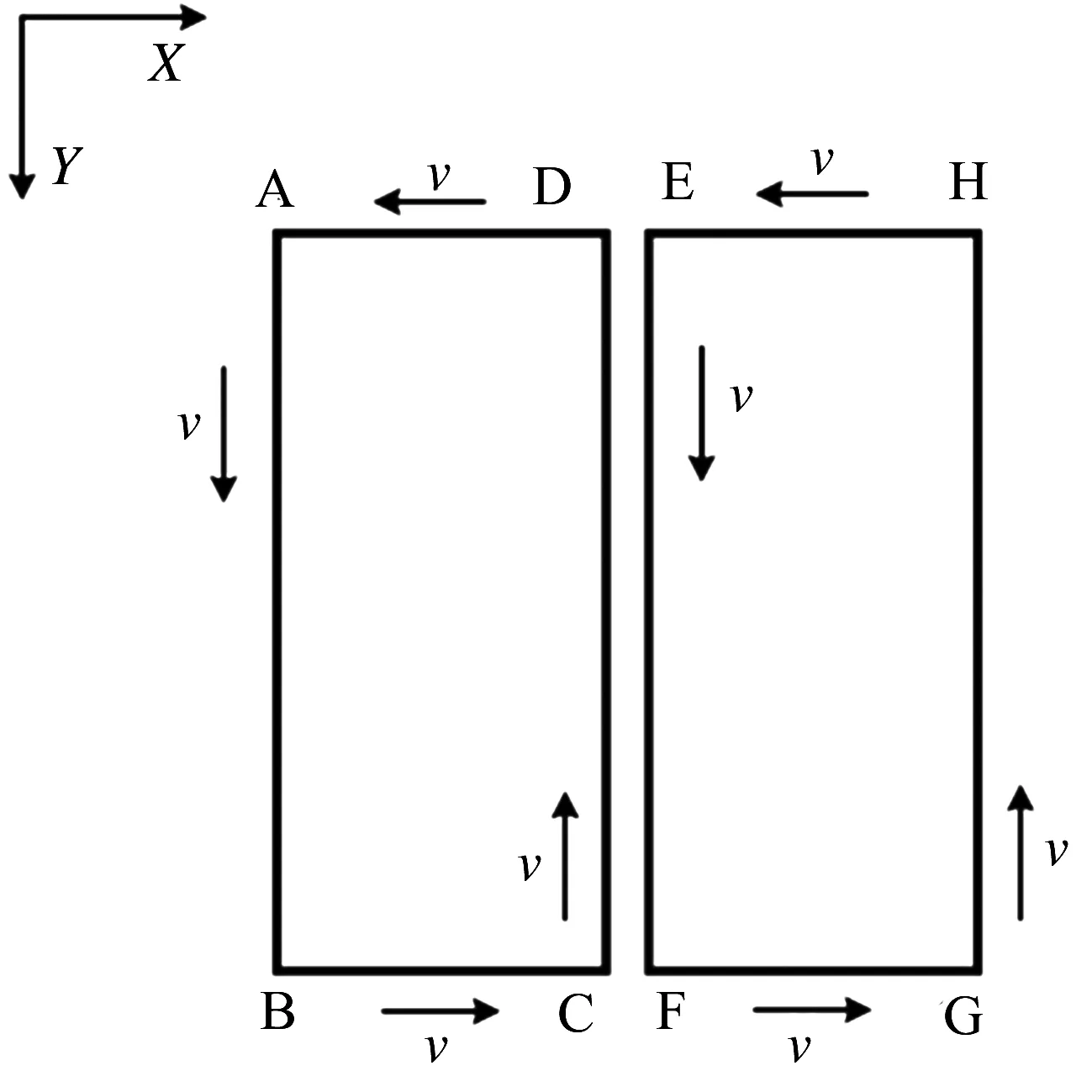
图4 双矩形图案加工任务

首先，通过栅格法将整个加工平面进行离散化表达.在加工平面上建立参考坐标系，即可以得到单机器人加工时任务点X/Y坐标值随时间变化的关系图，如图5所示，可知加工任务被转化为408个小栅格.

图5 双矩形加工任务点X/Y坐标值变化

之后将每个小栅格的遮挡时间计算出来，以设色图的形式进行表达，如图6所示.可以看出，图中CD、EF段所在的中间区域出现严重的重复遮挡现象，说明该区域造成了加工效能的浪费，同时双机器人协同加工时容易产生碰撞.

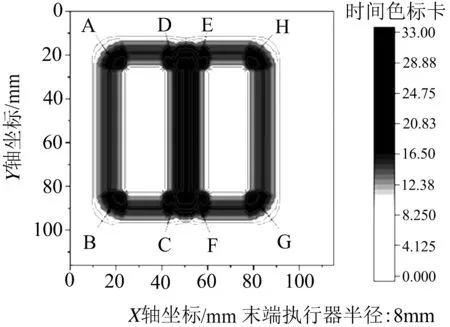
图6 双矩形图案加工任务的遮挡时间设色图

2.2 碰撞分析数学模型

通过建立碰撞分析矩阵可以得到双机器人协同加工的避碰方法.使用经栅格法离散化的任务点{p1,p2,p3,…,pn}建立如下碰撞分析矩阵A：

将经栅格法离散化的任务点{p1,p2,p3,…,pn}作为矩阵的次对角线，数值表示设定为2；矩阵其余元素代表机器人加工某一点pt时，若对其余任务点进行协同加工，是否会发生碰撞的描述，数值1代表会发生碰撞，数值0代表不会发生碰撞.即同时对点pt和点pn进行加工，若发生碰撞，则将点pt所在的行和列与点pn所在列和行的交点数值置1，否则为0.

通过矩阵变换进行分析，检测是否允许点pt和点pn同时进行加工，定义矩阵E为n阶单位矩阵，E(rx+ry)表示将矩阵的第y行加到第x行的初等变换，即：

令:

P=E(rt+rn)

B=PA

原碰撞分析矩阵A的次对角线的值全为2，经上述变换分析，检查新的矩阵B次对角线上的数值是否仍全为2，如果有的值不为2，则说明不允许同时对点pt和点pn进行协同加工，发生碰撞.

按照上述方法，针对图4所示的双矩形图案平面加工任务，建立碰撞分析矩阵，并将矩阵以设色图的形式进行表示，如图7所示.图中次对角线描述值为2的黑点代表离散化加工任务点{p1,p2,p3,…,p408}；灰色区域描述值为1，代表对灰色区域对应的行/列所在的任务点协同加工会发生碰撞；白色区域描述值为0，代表协同加工不会发生碰撞.

图7 双矩形图案加工任务的碰撞分析矩阵图

针对任务点p102和任务点p275，由碰撞分析矩阵图可以看出，点p102所在的行和点p275所在的列交点描述值为1，则表示不允许同时对点p102和点p275进行协同加工，否则会发生碰撞；同时从图中可以看出，由于末端执行器存在空间半径，当加工点p102时，不允许在p102左侧任务点{p86,p87,…,p101}位置及其右侧任务点{p103,p104,…,p118}位置插入其他机器人进行协同加工.

2.3 避碰规划

利用上述方法，通过对单机器人加工任务的二次分析，得出各任务点的协同加工情况，已知各任务点针对其余各点的协同加工情况，即可根据不同的原则规划出双机器人协同加工方法.

例如针对如图4所示的加工任务，设双机器人系统中的两个机器人R1和R2规格参数相同，每秒完成对1个任务点的加工.基于时间最短和路径连续原则，规划双机器人加工方法时，已知加工任务点和加工时间一一对应，当两个机器人同时开始加工，且加工的任务点数相同的情况下，即可保证时间最短，最短时间为单机器人加工时的二分之一.据此，从加工任务的中点点p205处开始进行碰撞分析，分析结果无碰撞，规划得机器人R1的加工任务为{p1,p2,p3,…,p204}，机器人R2加工任务为{p205,p206,p207,…,p408}，如图8所示.如若分析碰撞过程中发现碰撞点，则可对从碰撞任务点开始，将碰撞任务点的下一个任务点视为后续任务规划的新起点，继续采取时间最短原则对剩余未规划任务点进行碰撞分析，完成对全部任务点的任务规划；或者可以结合基于优先级的规划方法进行避碰加工，但该方法属于机器人路径规划的研究范围，失去了任务规划的意义.

图8 双矩形图案加工的规划矩阵图

3 结论

本文首先使用栅格法对单机器人加工任务进行离散化表达，将加工任务通过设色图的形式直观清晰地表达出来，使加工任务与加工时刻形成一一对应的关系；其次，建立碰撞分析数学模型，用矩阵图的形式对各个加工任务点的碰撞情况进行分析，分析出各任务点的协同加工碰撞情况；最后，按照实际加工要求，根据不同的加工原则，规划出系统的协同加工方法.实现了对双机器人系统平面协同加工的避碰协调规划，能够解决双机器人系统协同加工中的碰撞问题，通过仿真实验验证了该方法的可行性.

但是，本文仅对同类型双机器人系统平面加工的避碰方法进行了建模和实验说明验证，存在一定的局限性，在实际生产制造加工作业中，还需要考虑机器人型号不同及系统机器人的实际数目情况.本文方法的实际应用情况还有进一步拓展的空间，后续可按照本文方法思路对两个以上的多机器人系统的避碰加工方法进行研究；本文研究方法的过程中，省略了系统中机器人重定位，末端执行器抬起或下落的过程，后续可综合考虑实际情况，根据加工任务和系统结构的不同，加入优化的影响因子，完善碰撞分析模型，增强方法适应性.