带材拉伸弯曲矫直机系统能量的研究

刘 松，计 江，徐利璞，窦 锋，周存龙

(1.中国重型机械研究院股份公司，陕西 西安 710018；2.太原科技大学机械工程学院，山西 太原 030024；3.山西省冶金设备设计理论与技术省部共建国家重点实验室培育基地，山西 太原 030024)

0 前言

作为带材冷轧生产线要逐步实现国产化的重要设备之一，拉伸弯曲矫直机被广泛应用于精整机组、酸洗机组和镀锌机组等冷轧生产线上。由于带材拉弯矫直过程的变形机理非常复杂，国内的拉伸弯曲矫直理论研究始终基于多种假设的理想化模型，研究成果缺乏确凿的依据，且与实际情况出入很大。

目前对于拉弯矫直过程的研究多集中在压弯量、矫直力和曲率等局部参数的优化，缺乏对拉弯矫直系统的整体研究，这导致相应拉弯矫直设备缺乏理论依据并普遍存在着矫直范围小、产品精度低和自动化程度落后等问题。而且对于张力放大单元或弯曲单元的独立分析无法阐释整个拉弯矫直系统的真实状态，无法满足工程实际。

本研究旨在解决拉弯矫直理论缺乏宏观整体研究的现状，为相关工艺参数的优化提供理论依据。

1 工程背景

为解决国内拉弯矫直理论落后的被动局面，本文以某厂一弯一矫的连续拉伸弯曲矫直机为研究对象，对带材拉弯矫直过程进行了系统研究，并通过有限元模拟对带材拉弯矫直过程进行了模拟和计算，并对该过程中的系统能量变化进行了分析。为了反映拉弯矫直过程的真实变形情况，有限元计算的实体模型完全按照现场设备的尺寸进行建模，该模型的具体尺寸参数和各个弯曲辊标定如图1所示，并将1#、2#和3#弯曲辊所对应的弯曲单元分别称为I#、II#和III#弯曲单元。

图1 拉弯矫直机结构尺寸

2 有限元计算

假设带材在拉弯矫直过程中沿机组中心线对称变形，本文对该矫直机沿带材宽度方向取一半建立实体模型，如此既符合真实工况，又可以极大的降低有限元计算的时间。通过对实体模型进行网格划分和控制即可得到有限元模型。

有限元模型是进行有限元计算的基础，其建立方法可分为直接法和间接法，由于本文要处理的模型较为复杂且直接法较为复杂，因此采用对实体模型进行网格划分的间接法进行有限元模型的构建。

本文对实体模型选用Solid164单元进行网格划分。根据Solid164单元的几何特性，选定单元的形状为六面体。单元的网格大小和网格密度直接相关，而且在有限元分析中非刚性体单元的棱长比为1时，模拟的结果和变形情况比较符合实际情况。在带材厚度为2 mm时，建立的有限元模型如图2所示。由于带材厚度很薄，而设备的总体尺寸很长，因此仅将接触部位等单元显示在图2中。

图2 带拉弯矫直机有限元模型

对图2所示的有限元模型施加载荷和时间控制即可进行有限元计算。根据设定延伸率和现场使用情况，将入口和出口张力辊的转速分别设定为17.58 r/min和18.28 r/min，以此模拟电机带动张力辊来拖动带钢前进和带钢拖动矫直辊转动的真实工况。至于带钢与辊面间的摩擦力及其对张力放大的影响，定义完二者之间的接触后程序会自动进行计算无需人为干涉。时间控制主要是对计算终止时间的控制。计算终止时间是指进行有限元计算的终止时间，该时间是为了模拟真实场景所需要的物理时间而不是计算时间。带钢在弯曲辊和矫直辊上的弯曲变形是本研究的重点，因此将计算终止时间设定为由带钢刚进弯曲辊到带钢出矫直辊所需的时间，设定值为0.63 s。按照现场的响应时间，将II弯曲单元和III弯曲单元的压上时间设定为0.05 s。

3 数据后处理

对有限元计算得到的结果进行后处理。通过评价和分析不仅可以检查有限元模型的合理性，还可以直观分析拉弯矫直工艺的能量变化，并对相关参数进行优化和指导。

本文充分利用Ansys软件自身的通用后处理器Post1和时间历程后处理器Post26以及LS-Dyna提供的LS-Prepost后处理器对有限元模拟的计算结果进行分析和处理。

通过数据后处理可得如图3所示的带材拉弯矫直过程中某弯曲单元在不同阶段的能量分布。由图3可知，随着压弯量的增加，带材在此弯曲单元的塑性变形能逐渐增大。对各弯曲单元以及张力放大单元的能量数据进行筛分、统计和累加，得知整个拉弯矫直系统的能量变化。

图3 某弯曲单元不同阶段的能量分布情况

除此之外，通过对计算结果的数据后处理得到接触力(矫直力)、瞬时变形曲线(变形曲率)和竖向位移(压弯量)等结果，不过这些参数只能对拉弯矫直过程进行局部表征，因而本文不做详细论述。

4 能量分析

在拉弯矫直过程中，材质、压弯量、张力和摩擦状态等众多影响因素均会对矫后产品的品质产生影响，因此该过程的能量分析可对各影响因素的相互关系进行宏观和系统的整体研究。这是由于矫直力或变形曲率等参数仅是对该过程的局部表征，而能量变化才是各影响因素对该过程影响权重的系统表现。

4.1 拉弯矫直过程中的能量变化

根据拉伸弯曲矫直过程中的能量变化情况可以反映出整个体系中能量的转移和转化途径，尤其是可以为工艺参数的配置提供优化准则。图4是宽度和厚度分别为1 200 mm和2 mm的带材在拉弯变形过程中的能量变化。

由图4可知，在0～0.05 s内各个能量指标均呈非线性增长，其中动能的波动情况最为明显。这是由于0～0.05 s为下辊系按照矫直工艺的要求进行压上的时间，因此整个系统所需的能量的变化较大。

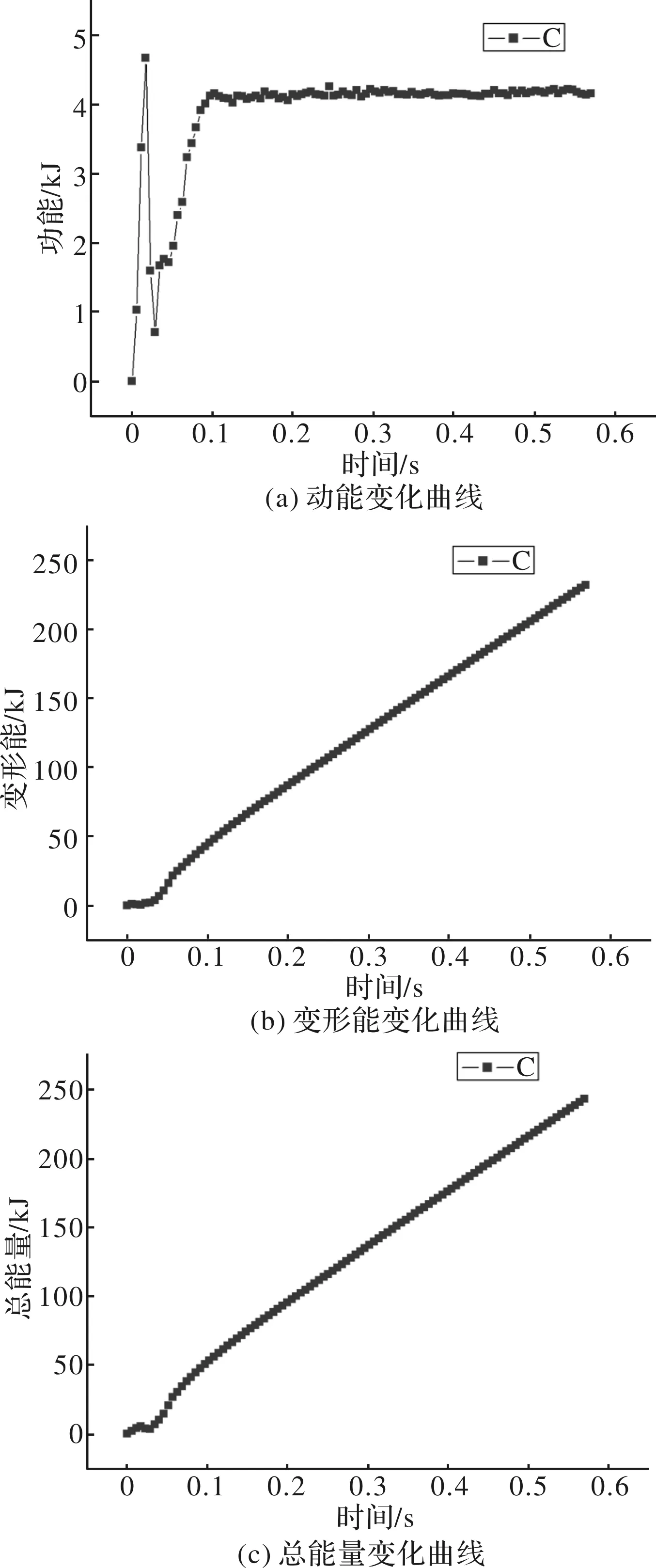
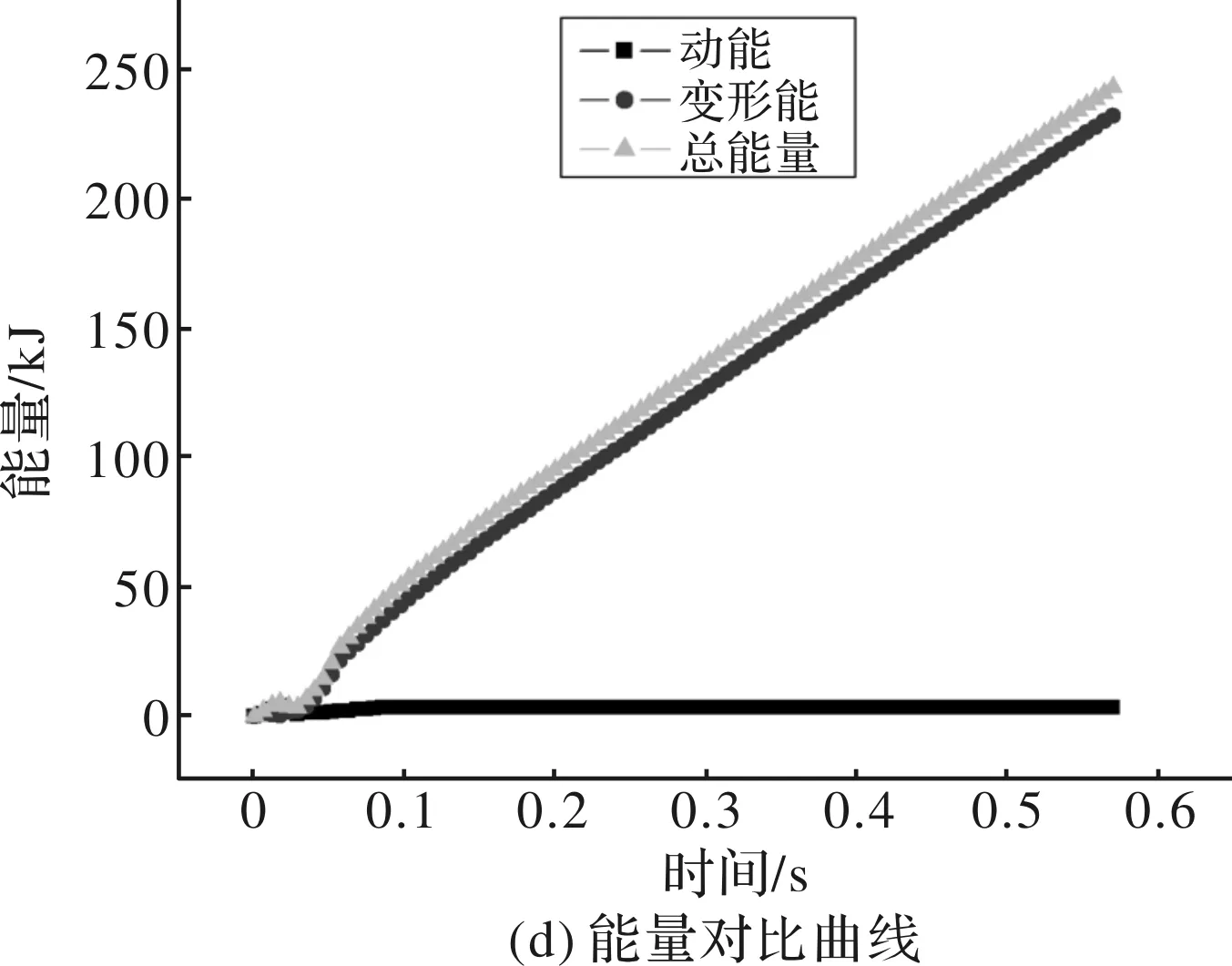
图4 能量随时间的变化情况

由图4a可知，由于带材在稳定矫直阶段的速度基本恒定，因此动能也基本恒定，约为4.1 kJ。由图4b和4c可知，在稳定矫直阶段带材的总能量消耗和变形能消耗线性增加，且变化趋势一样，这说明该阶段矫直带材所需要的电机功率基本恒定。由图4d可知，在整个变形过程中总能量和变形能的变化规律基本一致，而且总能量的大小与变形能相当，并且动能在总能量中占的比例很小。这说明在矫直过程中电机输出的能量主要用于带材的拉弯变形，而用于拖动带材和矫直辊所消耗的能量很少。此外，总能量的大小比变形能和动能的总和稍大，这是由于在有限元模拟中需要通过对沙漏能和其他能量的控制来实现计算的稳定和可靠进行，而且该过程中存在少量的内能。

图5a所示为对带材稳定矫直过程中的总能量进行的线性拟合。其中直线的斜率即为在整个矫直过程中电机的输出功率，约为402.84 kW。图5b为将带材在相同时刻的变形能与总能量求比值后的拟合。其中各个点表示了该时刻的机械效率，将稳定阶段的机械效率进行常数拟合后即为在整个时间历程上的机械效率，约为94.297%。

图5 电机功率与机械效率的确定

4.2 能量转移和转化

带材拉弯矫直过程的实质是能量的转移和转化过程。带材存在的板形缺陷其实是其内部不均匀原始变形能导致带材外观改变的现象。在拉伸弯曲矫直过程中，伴随电机能量向带材的逐步转移，带材内部不均匀变形能得以释放和均匀化并促使带材的外观和组织性能得以提高，其能量流动和转化过程为：电能→电机动能→张力辊动能→带材动能+带材弹性变形能→弯曲单元动能→带材塑性变形能。电机将电能转化为张力辊动能并拖动带材前进的过程中，带材具备一定的动能。而且由于张力辊的张力放大效应，带材受到拉伸而具备一定的弹性变形能。具备一定动能和弹性变形能的带材在依次经过各弯曲单元时，由于弯曲单元的反复弯曲作用而产生塑性变形能并将一部分动能转移至弯曲单元以保证带材表面不被划伤。

带材承受的张力放大单元提供的弹性变形能的主要作用是实现带材的中性层偏移，带材承受的弯曲单元提供的塑性变形能主要是实现带材变形能的均匀化。带材存在板形缺陷部位的不均匀变形能被拉弯矫直过程中的弹性变形能和塑性变形能相抵消便使得带材品质得以提高。在该过程中，弹性变形能的主要作用是使带材宽度方向的能量更为均匀，而随性变形能的主要作用是使带材厚度方向的能量更为均匀。

带材在拉弯矫直过程中，伴随着传动系统和带材与张力放大单元和弯曲单元的摩擦，部分能量转化为内能。

拉伸弯曲矫直过程中系统能量的转移和转化过程是电能转变为变形能、动能和内能。其实质是带材内部不均匀的原始变形能被张力放大单元和弯曲单元分别施加的弹性变形能与塑性变形能的抵消和均匀化。该过程中各种能量在系统能量中的占比如图6所示。

图6 能量占比关系

4.3 能量与工艺参数的关系

带材的材质、规格、压弯量、张力和延伸率等诸多因素等均会对拉弯矫直过程中的能量产生影响。本文以张力为研究对象，在其他工艺参数固定的情况下，分别采用1/12、1/10、1/8和1/6四种张力系数(张力与屈服强度的比值)进行了模拟计算，变形能与张力的关系如图7所示。

由图7可知，对于较厚的带材，在一定范围内其变形能随张力的增大而减小。这是由于对于较厚带材，弯曲单元对带材表层的塑性变形能影响较大，而对其中心层附件的塑性变形能影响较小，但是张力所引起的弹性变形能在带材横断面上是均匀分布的，因此对带材原始变形能的抵消所发挥的作用更大。

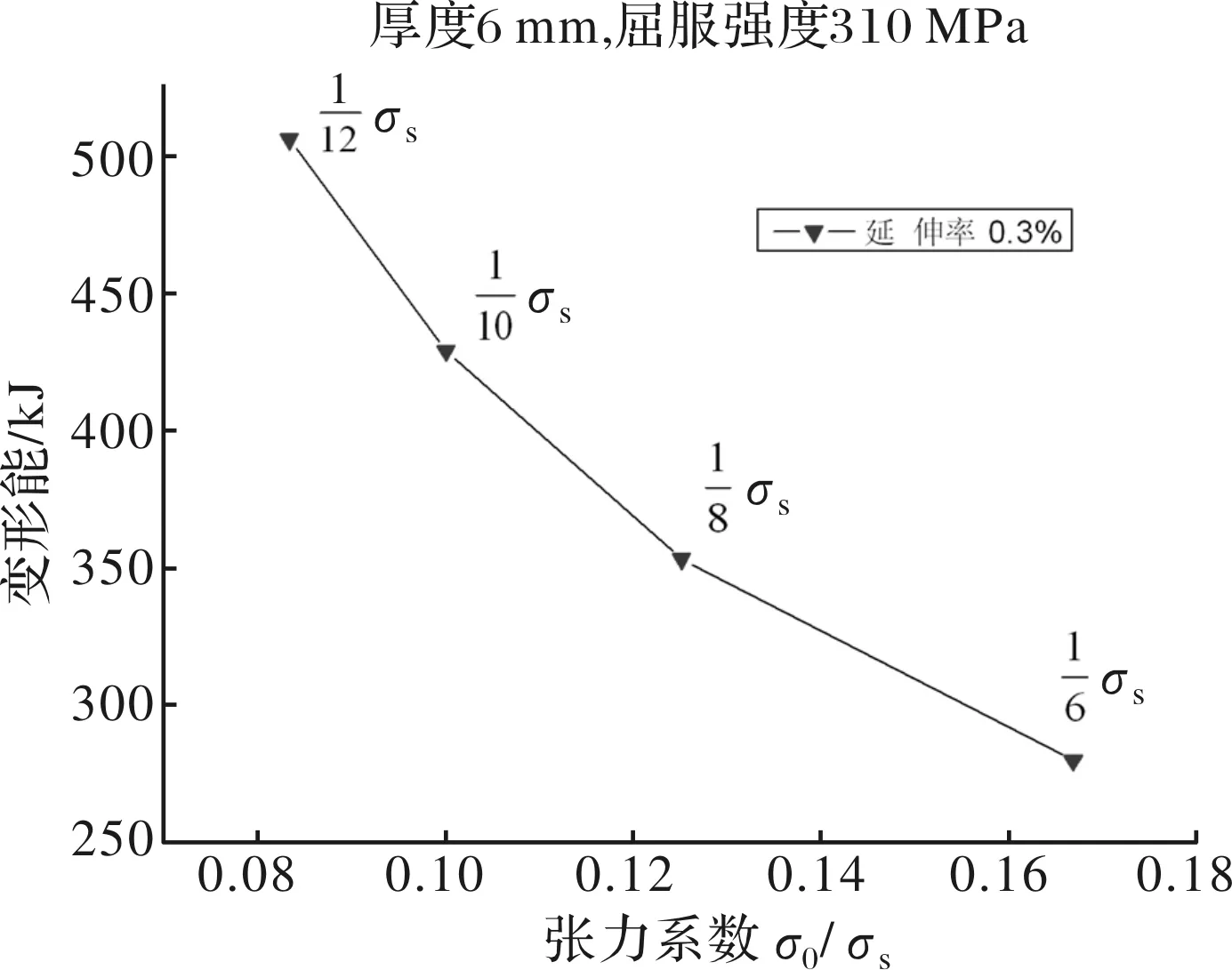
图7 变形能与工艺参数间的关系曲线

所以对于偏厚的带材进行拉伸弯曲矫直时，应将张力取得偏大些，这会使得变形耗能更小从而达到节能降耗的目的。

4.4 能量分析的意义

通过有限元计算可以准确得知拉伸弯曲矫直过程中的能量消耗和机械效率，对矫直设备的电机优选有一定的帮助。系统能量分析不仅对矫直设备研究具有重要意义，而且可以为工艺参数优化提供理论支撑。

拉伸弯曲矫直过程中带材的延伸率直接决定了产品的板形和品质。但是由图8可知，针对相同规格和材质的带材，为实现相同的延伸率存在着压弯量和张力的多种组合。因而在满足延伸率的各工艺参数组合中，选择最优的一组是极具意义的。尽管不同工艺参数组合可实现相同的延伸率，但其消耗的能量是不同的。因此通过系统能量分析的方法可获得指定延伸率下耗能最低的压弯量和张力设定，为矫直工艺参数的优化提供了准则并可充分满足低碳环保的绿色钢铁的要求。

图8 某延伸率所对应的多种工艺参数组合

5 结束语

根据某厂拉伸弯曲矫直机的原始结构尺寸和该矫直机的现场使用情况，建立了相应的有限元模型，模拟了厚度、宽度和屈服强度分别为2 mm、1 200 mm和310 MPa的拉弯矫直过程，对带材拉伸弯曲矫直过程中的系统能量进行了分析，得到了局部区域的瞬时能量分布云图，分析了系统内各种能量随时间的变化曲线，得到了电机功率和机械效率。

分析了拉弯矫直过程中的能量转移和转化途径以及各种能量的占比。研究了对工艺参数和能量间的关系，在一定范围内，变形能随张力增大呈减小趋势。提出了以变形能最小作为工艺参数优化的准则。通过拉弯矫直过程的系统能量分析可以宏观表征该系统的整体状态，既能优化矫直设备中电机等的相关参数，又为矫直工艺中压弯量和张力的参数优化提供准则和理论依据。