基于新能源消纳的峰谷平时段划分方法
薛晨, 任景, 崔伟, 彭明侨, 肖晓明, 刘颖, 谭玉东
(1.国家电网公司 西北分部,陕西 西安 710048;2.长沙理工大学 电气与信息工程学院,湖南 长沙 410114;3.国网湖南省电力公司 经济技术研究院,湖南 长沙 410004)
0 引 言
随着多地区新能源并网,新能源在发电侧的占比日益增加[1]。但部分地区用电峰谷期与新能源发电供需不平衡,出现弃风和弃光等降低新能源消纳的现象[2]。目前,大多数研究从调整电价角度实现新能源消纳增加的目的。文献[3]和文献[4]通过改变峰谷平电价来提升新能源的消纳度。文献[5]通过在发电侧建立储能系统来促进新能源的消纳。部分文献通过聚类分析用户负荷特性,如模糊聚类法[6]、阈值优化函数法[7]和密度聚类[8],对负荷峰谷隶属度聚类并划分峰谷平时段,但忽略了新能源出力及消纳问题。
本文提出了一种在原有峰谷平电价不变的场景下,对峰谷平电价所属时段进行重新划分方法,通过用户对于新的峰谷平时段进行响应,达到提升新能源消纳的目的。
1 基于消费者心理学的用户响应模型
本文引入基于消费者心理学[9]的用户响应模型,不同时间的用户侧负荷会随其所属时刻对应电价之间的差值改变而改变,对于这一变化,用负荷转移率进行量化表示,如图1所示。电价差对用户的刺激包含三个区域,分别为死区、饱和区以及线性区。当电价差处于死区时,用户并无意愿改变原有的用电行为;当电价差处于线性区时,用户将对电价差的刺激作出响应,且负荷转移率随电价差值呈正比关系;当电价差处于饱和区时,用户负荷的转移量达到峰值,即用户可转移负荷已全部转移。
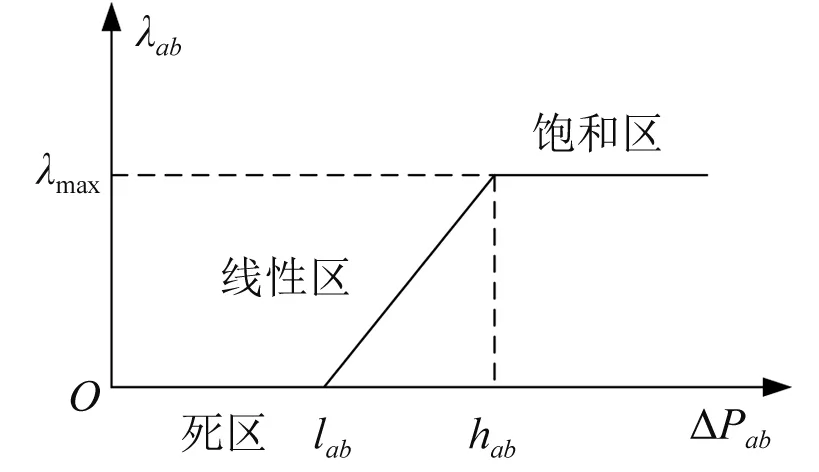
图1 负荷转移率
负荷转移率与电价差的关系用式(1)表示。
(1)
式中:a、b为时段;ΔPab为a至b时段电价差;lab、hab分别为死区与线性区上限值;Kab为线性区斜率;λab为a至b时段的负荷转移率。
由此可得到峰-谷、峰-平、平-谷负荷转移率分别为λfg、λfp和λpg,进而拟合得到响应后的用户负荷如式(2)所示。
(2)
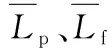
考虑到时段调整前后峰谷平时段总时长与调整前可能不一致,对式(2)进行修改。
(3)
通过拟合某省电网负荷数据,基于消费者心理学的用户响应模型参数如表1所示。
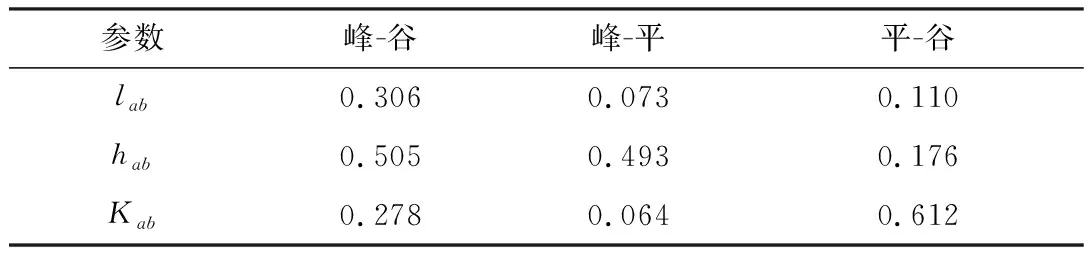
表1 用户响应模型参数
2 基于新能源消纳的峰谷平时段优化模型
2.1 促进新能源消纳模型
(1) 当用户响应后负荷增加,则保持其他机组不变,优先增加新能源消纳,直至新能源消纳量达到上限时,再增加其他机组发电。上述关系如式(4)、式(5)所示。
当ΔL(t)>0,且Lx0(t)+ΔL(t)≤Lc(t)时:
(4)
式中:ΔL(t)为响应前后用户负荷增量;Lx0(t)、Lx(t)分别为系统响应前后t时刻新能源的消纳量;Lc(t)为t时刻新能源出力;Lq0(t)、Lq(t)分别为系统响应前后t时刻其他机组出力。
当ΔL(t)>0,且Lx0(t)+ΔL(t)>Lc(t)时:
(5)
(2) 当用户响应后负荷减少,则优先降低其他机组出力,保持新能源消纳不变,当其他机组出力降到限定值时,再降低新能源消纳。上述关系用式(6)、式(7)表示。
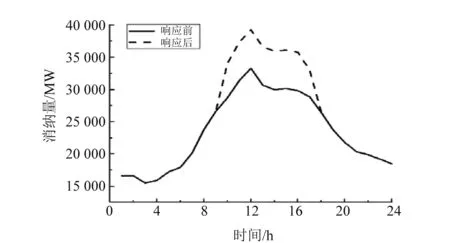
当ΔL(t)≤0,且Lq0(t)+ΔL(t) (6) 当ΔL(t)≤0,且Lq0(t)+ΔL(t)≥Lq0_min时: (7) 式中:Lq0_min为其他机组出力最小值。 相较于传统依据负荷进行峰谷平时段划分,当需要同时考虑新能源消纳时,应先对新能源出力进行处理。将新能源出力看成数值为负数的负荷,与用户侧负荷构成等效负荷。等效负荷中数值最大与最小的时刻分别对应峰期与谷期,其他时刻则根据峰谷隶属度来进行划分,计算公式如式(8)所示。 (8) 式中:μft、μgt分别为峰、谷隶属度;maxL、minL分别为负荷峰值、谷值。 在式(8)中,某时刻峰隶属度越大,则说明属于峰期的可能性越高;谷隶属度越大,则说明属于谷期的可能性越高。 (9) 式中:m1为峰隶属度阈值;m2为谷隶属度阈值。 在考虑促进新能源消纳的同时,也应考虑用户响应前后总用电费用的变化,引入用户电费满意度: (10) 式中:Q、Q0分别为用户响应前后总用电费用;θ为用户电费满意度。 用户响应后总的用电费用越低,电费满意度越高,则说明用户对本次参与响应的满意程度越高,参与下一次响应的意愿程度也越高。 在负荷转移率的各个参数及用户初始负荷与初始电价已确定的情况下,新的峰平谷时段划分主要由峰谷隶属度阈值决定,因此将决策变量设为峰谷隶属度阈值m1、m2。 同时考虑新能源消纳以及用户费用时,以新能源消纳最大化以及用户电费满意度最高为目标函数,计算公式如式(11)所示。 (11) 式中:θ为用户电费满意度;ω1、ω2为权值。 (1) 时段约束:峰谷平每个时段长度≥6 h; (2) 用户费用约束:响应前后总电费变化范围为-1%~0。 本文以某地区实际负荷数据作为案例验证方法的有效性,其初始峰谷平时段与电价如表2所示。 表2 初始峰谷平时段及电价 图2为基于新能源消纳的峰平谷时段划分仿真流程图,具体流程如下。 图2 仿真流程图 (1) 数据处理:对某省电网负荷数据进行整理得到新能源出力数据、消纳数据、负荷数据及初始峰谷平时段与电价。 (2) 设立目标函数及约束条件:基于前文所提,建立新能源消纳最大化及用户电费满意度最高的目标函数,其中权值ω1、ω2均为0.5;建立时段及用户费用约束条件。 (3) 优化求解:本文采用改进粒子群算法对峰谷隶属度阈值进行优化求解。 (4) 新峰平谷时段划分:依据式(9)得到新的最优峰平谷时段。 (5) 响应前后新能源消纳结果对比。 根据3.1小节的仿真流 ,优化求解得到峰谷隶属度阈值m1=0.622 4,m2=0.674 7,因此得到响应后峰谷平时段,如表3所示。 表3 响应后峰谷平时段 图3给出了用户对新的峰谷平时段响应前后新能源消纳曲线对比结果。 图3 新能源消纳曲线 表4给出了用户对新的峰谷平时段进行响应前后的新能源消纳量和总用电费用对比结果。 表4 响应前后数据对比 由图3及表4可以看出,用户对新的峰谷平时段进行响应后,新能源消纳占比从86.13%上升至93.05%,提升了6.92个百分点,即时段的调整达成了促进新能源消纳的目的。同时,用户总用电费用从840 839.7 万元降至835 037.9 万元,降低了0.69个百分点,提升了用户满意度。 本文基于消费者心理学,提出了一种以新能源消纳最大以及用户费用最低为目标函数的峰谷平时段划分新方法,采用粒子群优化算法对峰谷隶属度阈值进行优化求解,达到调节峰谷平时段促进新能源消纳的目的。以某省电网实际算例可知,用户响应新的峰谷平时段后,用电费用降低了0.69%,同时使得新能源的消纳提升了6.92个百分点,验证了本文方法的有效性。2.2 峰谷隶属度阈值
2.3 用户电费满意度
2.4 目标函数
2.5 约束条件
3 案例仿真分析
3.1 仿真流程图与初始数据

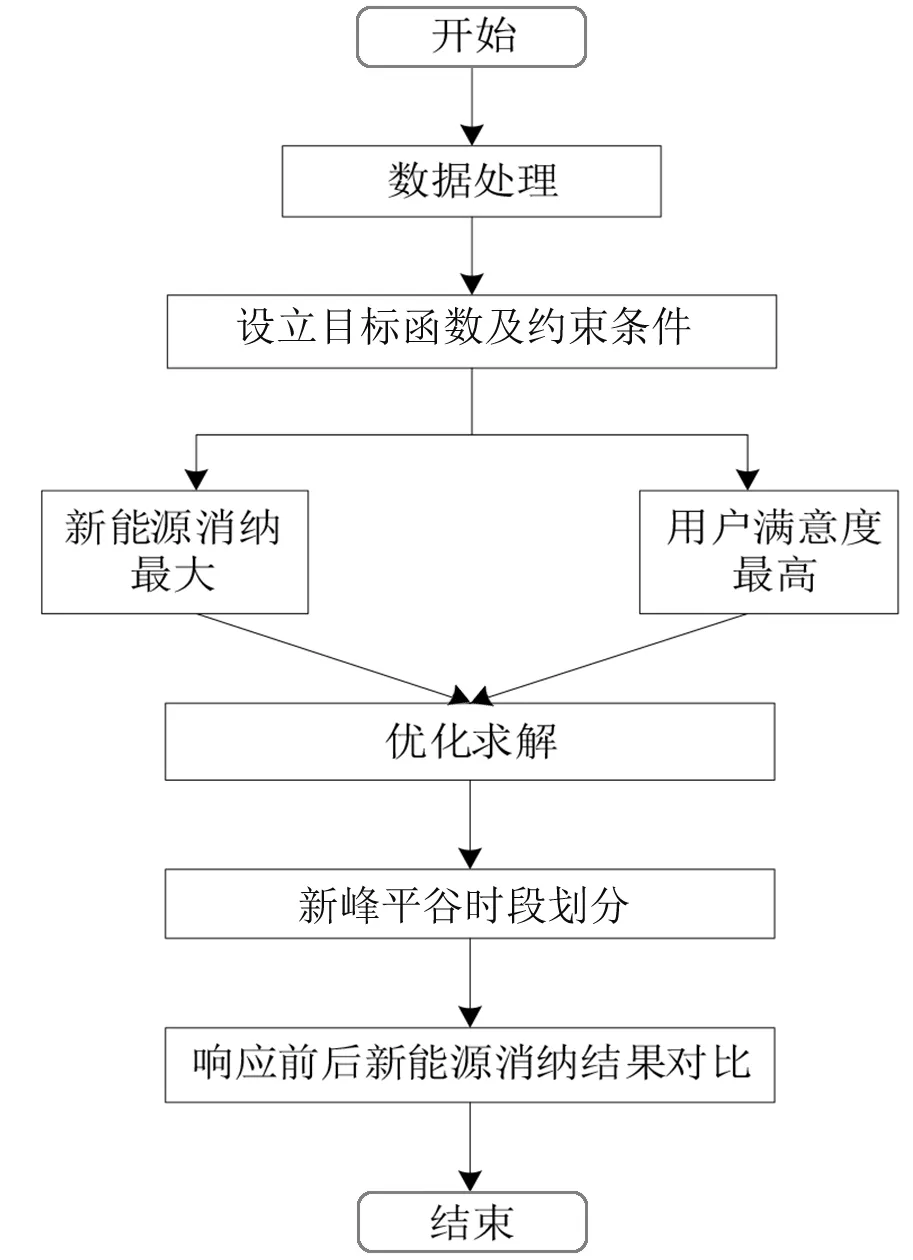
3.2 案例分析


4 结束语

