计及电能质量的分布式电源并网优化研究

王亚男， 陈虹

(1.陕西能源职业技术学院，陕西 咸阳 712000；2.国网江苏省电力有限公司 常州供电分公司，江苏 常州 213000)

0 引 言

随着人们对环境和可持续发展的日益重视，分布式电源因具有环保高效等优点而获得快速发展。分布式电源并入配电网的情况越来越多[1]，但分布式电源功率的不确定性和波动性会给配电网的运行造成很大的影响。若不对分布式电源进行合理的优化配置，分布式电源并网会给配电网的安全稳定性带来很大的负面影响。而随着经济的发展和高科技设备的广泛应用，电力用户对配电网运行的电能质量要求越来越高[2]。因此需对分布式电源并网优化进行深入研究，以便更好地提高配电网运行的经济性和电能质量水平。

国内外针对分布式电源并网的影响及其优化已经做了一定的研究工作。文献[3]研究表明分布式电源并网可在一定程度上降低配电网的损耗，且降低程度与并网位置有关。文献[4]研究发现分布式电源并网对配电网的电压有一定的抬升作用，但并网容量超过一定程度时则会使电压出现超越上限的问题。文献[5]发现分布式电源的合理配置可降低配电网的节点电压谐波畸变率。文献[6]将遗传算法应用于配电网分布式电源并网优化模型求解，但只考虑了配电网的经济性。文献[7]在分布式电源并网优化模型求解时采用粒子群算法，但也未考虑配电网电能质量的影响。目前，分布式电源并网优化研究一般均未将电能质量作为优化目标，且采用的智能求解算法存在着寻优效果不理想的问题。

本文建立了综合考虑配电网经济性和电能质量的分布式电源并网优化模型，模型的求解则提出了改进的遗传粒子群算法。

1 分布式电源并网对配电网的影响

1.1 分布式电源输出功率特性分析

分布式电源主要包括分布式光伏和分布式风电两种。分布式光伏的输出功率Ps与太阳光照射强度s之间的关系用函数表示为：

(1)

式中：Psn、sn分别为分布式光伏的输出功率额定值和额定光照强度。

根据研究表明，太阳光照强度s在一定时间段内是一个近似服从Beta分布的随机变量[8]，其概率密度函数f(s)表达式为：

(2)

式中：Г为伽马函数；α,β分别为Beta分布的形状参数和尺寸参数；smax为光照强度的最大值；t为时间。

分布式风电的输出功率Pw与风速v的关系用函数表示为：

(3)

k1=Pe/(vr-vci)

(4)

k2=-k1vci

(5)

式中：vr、vci、vco分别为额定风速、切入风速和切出风速；Pe为分布式风电的输出功率的额定值。

根据统计数据分析表明，某地区的风速v服从Weibull分布[9]，其概率密度函数f(v)表达式为：

(6)

式中：k、c分别为Weibull分布参数的形状和尺寸系数。

1.2 影响理论分析

分布式电源并网后会影响配电网的潮流分布，进而影响配电网的电压分布及电压偏差。图1为配电简化结构图。图中：配电网始端电压为U0；假设U0恒定不变，配电网基准电压为UB；配电网节点总数为N；节点X的负荷为PX+jQX，馈线m的线路长度为lm；等值阻抗Rm+jXm=lm(r+jx)；r、x分别为单位长度的线路电阻和电抗。

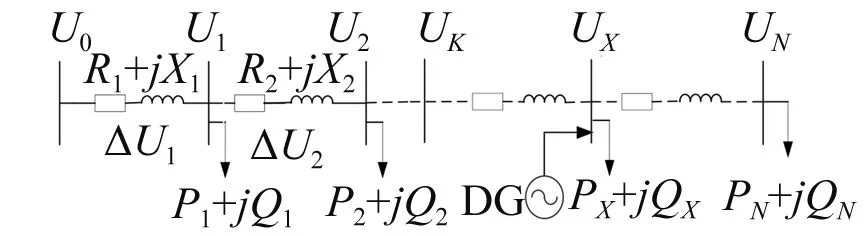
图1 配电网简化结构图

无分布式电源并网时，配电网节点K的电压UK、电压偏差△UK%、网损Pl分别为

(7)

(8)

(9)

当配电网有分布式电源并网时，假设节点X并网的分布式电源输出功率为PDGk+jQDGk，此时配电网节点K的电压UK、电压偏差△UK%、网损Pl分别为：

(10)

(11)

(12)

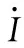
(13)

分布式电源本身的谐波主要受其控制系统的影响，分布式电源产生的正序和负序谐波会与配电网系统本身的谐波发生相互耦合的影响。

2 分布式电源并网优化模型

2.1 并网优化数学模型

分布式电源并网优化是指在满足一定的约束条件下，通过对并网位置和并网容量的调节来达到相关目标[11]。本文对并网后配电网经济性和电能质量做综合评估，经济性评估指标选取网络损耗，电能质量评估指标选取节点电压偏差和电压总谐波畸变率。并网优化的目标函数为：

(14)

(15)

(16)

(17)

式中：c1、c2和λ1、λ2为权重系数，满足c1+c2=1，λ1+λ2=1；Ploss、Ploss,B为网络损耗及其标准值；△UK%、△UB%为节点电压偏差及其标准值；THDu,K、THDu,B为节点电压总谐波畸变率及其标准值；N为节点总数；Ui、Uj为节点i、j的电压；Gij为互电导；δi、δj为电压相位角；UK、UB为节点实际电压和额定电压；Urms,K、U1rms为节点谐波电压及基波电压的有效值。

分布式优化并网优化需满足一定的约束条件：

(18)

式中：Pi、Qi为节点i的有功和无功负荷；PDGi、QDGi、PDGimin、PDGimax、QDGimin、QDGimax为节点i并网的分布式电源有功出力和无功出力及其对应的最小出力、最大出力;Gij为互电导；Bij、θij为节点i和节点j之间电纳和相角差;Ui、Uj为节点i、j的电压;Umin、Umax为节点电压的最小值和最大值;Pmax为并网的分布式电源总容量最大值。

2.2 并网优化模型求解方法

粒子群算法是一种通过随机初始化一群粒子来获得最优解的群体智能算法，传统粒子群算法存在着收敛速度较慢的问题[12]。本文将混沌序列思想应用于粒子群的的初始化，粒子群位置xk+1为：

(19)

当满足xk=xk-m(m=1,2,3,4)或xk=0, 0.25, 0.5, 0.75时，位置xk+1的更新公式为：

xk+1=T(xk)+0.1·rand(0，1)

(20)

式中：k为迭代次数；rand(0,1)为随机数。

(21)

粒子群算法局部搜索能力较强，但其在全局性方面存在不足，而遗传算法则刚好相反：局部搜索能力较弱，但全局性较强，遗传算法和粒子群算法具有很好的互补性。本文将两种算法进行有效融合：首先使用粒子群算法进行局部寻优以获得局部最优解，并将其传递给遗传算法，然后利用遗传算法进行全局寻优，图2为本文遗传粒子群融合算法的基本流程。

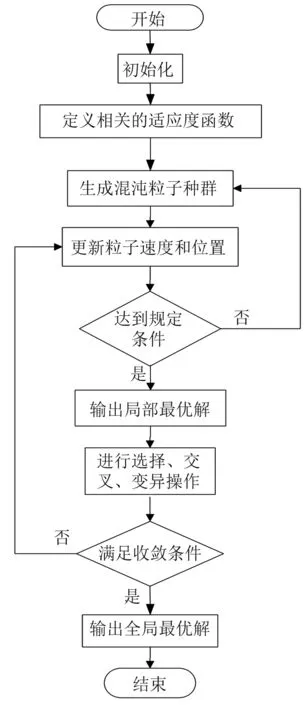
图2 遗传粒子群算法基本流程

3 分布式电源并网实例分析

3.1 分布式电源并网仿真模型

本文选取IEEE 33节点配电网为分布式电源并网的系统，系统参数详见文献[13]。图3为其结构图，利用PSCAD/EMTDC软件建立相应的仿真模型。某地区典型日下的分布式电源输出功率曲线如图4所示。

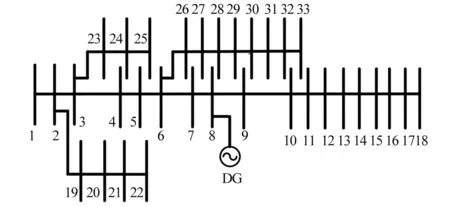
图3 IEEE-33配电网结构图

图4 分布式电源输出功率曲线图

3.2 并网优化结果分析

根据本文建立分布式电源并网优化数学模型，并分别与遗传算法、粒子群算法和退火蚁群法进行对比，优化后获得的网络损耗和电能质量如表1所示。图5为3个分布式电源并网时的优化收敛过程。图6为优化后的各节点电压谐波畸变率情况。

表1 分布式电源并网优化结果

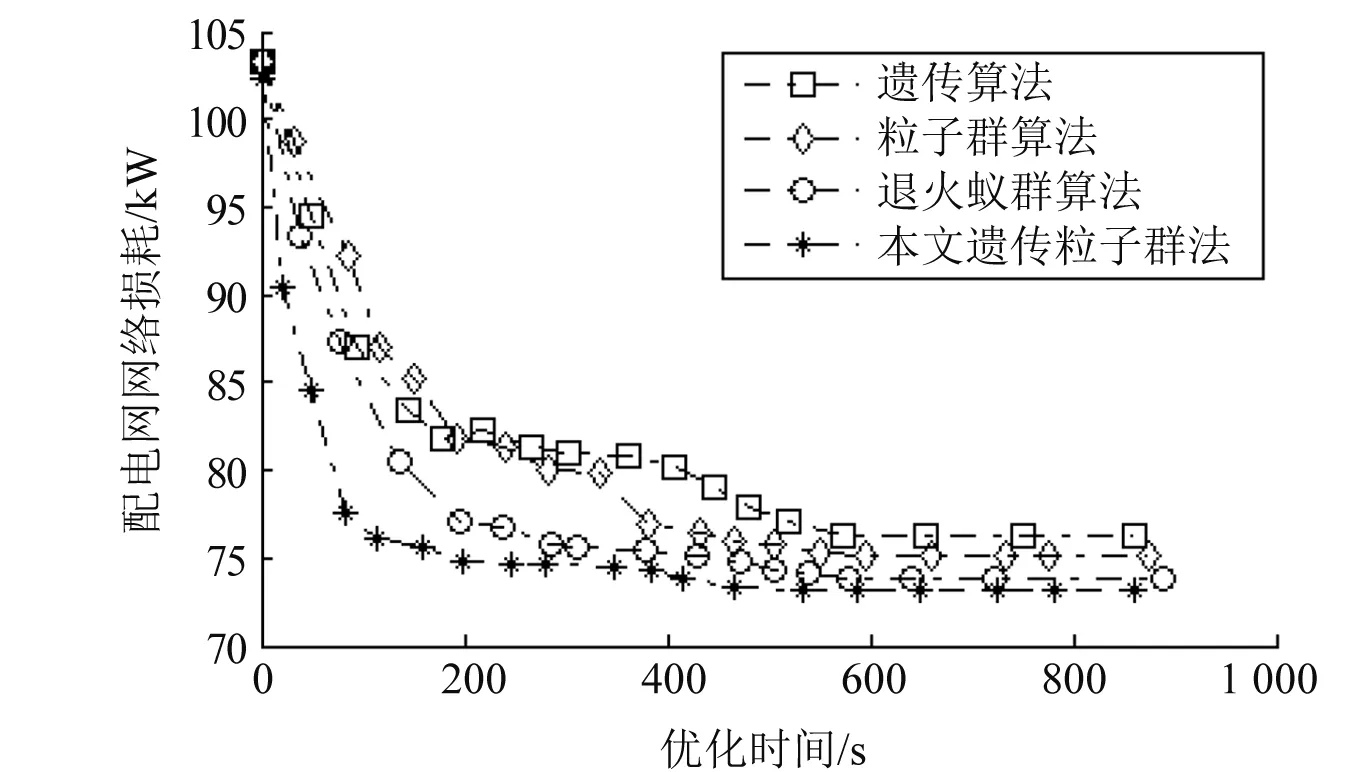
图5 并网优化收敛曲线图

图6 配电网节点电压谐波畸变率

根据表1的结果可知，对分布式电源优化并网后可有效降低配电网的网络损耗、节点电压偏差和电压谐波畸变率，且随着分布式电源数量的增加，配电网经济性和电能质量指标变得更加优良。由图5可知，对于3个分布式电源并网时，当其未进行并网优化时，其网络损耗(约103 kW)要比无分布式电源并网时(192.36 kW)降低46 %左右，而优化后的配电网网络损耗(约73 kW)要比优化前进一步降低25 %左右。由图6可知，分布式电源并网前的电压谐波畸变率最大值达16 %，而优化并网后的电压谐波畸变率出现明显的降低。对分布式电源进行并网优化能有效地提高配电网的经济性和电能质量，而本文提出的改进遗传粒子群算法在模型的求解中具有很好的优越性，寻优后获得的网络损耗、节点电压偏差和电压谐波畸变率在四种算法中均是最低的，且本文算法收敛特性优良，收敛时间(532.8 s)也是最短的。

4 结束语

本文建立了综合考虑配电网经济性和电能质量的分布式电源并网优化数学模型，通过仿真实例对不同并网数量的分布式电源进行并网优化分析。结果表明，分布式电源并网对配电网有较大的影响，分布式电源优化并网后可有效降低网络损耗、节点电压偏差和谐波畸变率，且分布式电源数量越多，优化并网后的经济性和电能质量指标越优良。而本文提出的改进遗传粒子群算法在模型的求解中具有很好的优越性，寻优后获得的经济性和电能质量指标是最好的，且本文算法具有优良的收敛特性。本文研究成果可为分布式电源的并网及配电网经济性和电能质量的提高提供有效参考和技术指导。