计及高渗透率可再生能源接入的配电网节能规划研究

梁作宾， 刘国明， 齐向， 张杰， 袁飞， 王庆

(1. 国网山东省电力公司泰安供电公司，山东 泰安 271000；2. 国网山东省电力公司 发展策划部，山东 济南 250001)

0 引 言

在电力系统中，配电网的损耗情况最为严重，因此在节能规划时，配电网具有最大的节能潜力[1-2]。同时，随着分布式风能、光伏的大规模接入，配电网中的可再生能源比例呈现高渗透趋势[3]。在不同渗透率和不同可再生能源选址定容方案下，会影响配电网整体改造方案的决策。因此，同时考虑可再生能源规划和配电网改造方案具有现实意义。

当前，针对配电网节能改造的方法比较多。文献[4]从全寿命周期成本角度出发，对变压器、配电线路和无功补偿进行改造，建立了全寿命周期成本效益模型。文献[5]从配电网优化运行角度考虑，用等值电路法推导含有载调压调容配变的有功损耗，提出了一种含有载调压调容配变的配电网节能降损动态优化模型,最后求解得到有载调压调容配变等设备动作方案。文献[6]同样从运行优化的角度，综合考虑了分布式电源等调压设备的参与，通过优化电压控制模型，实现配电网的节能效益。文献[7]提出了一种考虑分布式电源接入的配电网重构算法，通过网络重构有效地降低了网损，并验证了算法的有效性和全局收敛性。

综上所述，在现有的配电网节能相关研究中，主要是通过配电设备更换、优化运行状态实现降损节能，很少将可再生能源考虑在内，更少将可再生能源规划问题同配电网节能问题一同考虑。本文将把可再生能源规划与配电网的综合改造作为一个整体进行考虑，体现了可再生能源规划与配电网节能改造之间的相互影响，最后实现两者的最优决策。

1 分层分区节能规划整体思路

首先采用考虑资源时空特性的方法对新增可再生能源容量与布局进行规划，即图1中阶段A。

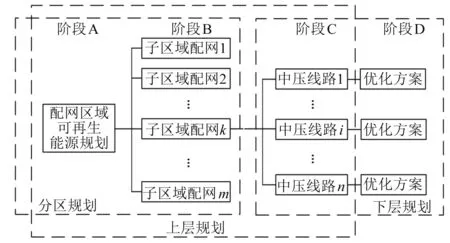
图1 分层分区节能规划思路

其次根据规划区域不同线路的降损潜力，对规划区域进行分区，并对投资成本进行初步分配(阶段A到阶段B)。

随后在全局配电网中以新增可再生能源投资成本最小、线路差异化改造成本最小和节能效益最高为目标函数，建立上层规划模型(包含阶段A、阶段B和阶段C)。

再次用前推回代法，代入线路运行数据，求得各条线路上的降损值，优化得到各线路最具节能效益的综合改造方案(阶段C到阶段D)，即下层规划。

最后通过上下层模型迭代，实现节能改造方案的优选和投资分配。

2 可再生能源容量与布局优化建模

考虑到采用和声搜索算法对双层模型进行迭代求解，为了提高算法的收敛速度及效率，首先对可再生能源容量和布局进行规划，形成迭代初始数据。文献[8]给出了一种考虑资源时空特性的可再生能源容量与布局规划模型，具体规划流程如图2所示。

图2 可再生能源规划流程

第一步，将规划区域按照纬度0.5°、经度0.67°划分得到地理网格模型，并基于MERRA(modern era retrospective analysis for research and applications)气象数据表征各地理网格的资源时空特性。

第二步，采用单位可再生能源容量出力序列描述每个地理网格资源的时序变化，从而得到可再生能源的出力模型。

第三步，在考虑到各地理网格的地形和海拔等因素的影响时，计算可利用土地的总面积，并结合风电机组和光伏电池板的安装特点，得到每个地理网格最大的可开发容量。

可再生能源电源规划模型的目标是新增风电和光伏发电装机容量的投资和运行成本最小化。

(1)

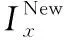
可再生能源容量与布局规划时考虑如下约束条件：

(1)可再生能源发电约束。并网风电与光伏发电的时序出力约束为:

(2)

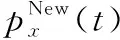
(2)可再生能源占比约束：

(3)

式中：λL为区域可再生能源发电量相对负荷电量的占比，通过设置不同的λL，可以得到可再生能源不同的渗透率；PL(t)为区域电网在时刻t的负荷功率。

(3)时序功率平衡约束:

(4)

3 建立双层模型

3.1 上层规划模型

将新增可再生能源投资及运行成本计入配电网节能改造总成本，建立同时考虑投资总成本和降损效果的上层模型，具体如下：

(5)

(6)

(7)

(8)

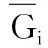
3.2 下层规划模型

下层模型实现各条线路的综合改造成本及网损费用最低，具体如下：

(9)

式中:投资回收因子μ=β(1+β)n/(1+β)n-1；Ωj为线路j中支路的集合；β为折现率；n为设备经济使用寿命；cL、cT、cMD、cM分别为线路改造投资、变压器改造投资、无功补偿设备投资和维护投资；ΔPj为各支路的有功损耗；a为单位电价；T为各设备年等效运行小时数。

同时，下层规划模型需要满足如下约束条件：

(1) 潮流方程约束。结合图3对配电网潮流方程约束进行说明。

图3 配电网结构图

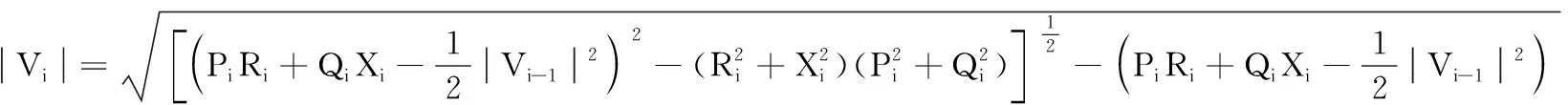
(10)

(11)

(12)

(13)

(14)

(15)

(16)

式中:Vi为节点电压；Ri、Xi为线路阻抗；Pi、Qi为线路前端的有功功率和无功功率；PLj、QLj为节点的负荷功率；ΔPi、ΔQi为线路的功率损耗；k为迭代次数。

(2) 线路改造约束。

Iimin≤Ii≤Iimax

(17)

式中:Iimax、Iimin为各支路电流的上下限。此约束条件可以防止电流越限，保证配电网运行在安全电流范围内。

(3) 变压器负载率约束。

βmin≤β≤βmax

(18)

式中:βmax、βmin为变压器运行负载率上下限。负载率是考核变压器改造的重要考核指标。

(4) 无功补偿设备约束。

(19)

Vimin≤Vi≤Vimax

(20)

Qimin≤Qi≤Qimax

(21)

式中:Gi为无功补偿装置安装费用；amdi为单位容量投资成本；Qi为安装容量；Vimax、Vimin、Qimax、Qimin分别为节点电压上下限、无功补偿装置容量上下限。

4 模型求解

针对含有高渗透率可再生能源的配电网差异化节能规划模型，求解步骤如图4所示。

图4 模型求解框架图

(1)对第2章中所提可再生能源规划模型进行求解。该模型是一个只包含连续变量的大规模线性规划问题，得到可再生能源的初步规划方案，并同现有网架信息一起初始化和声记忆库。

(2)将和声记忆库中的数据传递到下层，通过前推回代求得线路优化改造方案，将结果向上层模型传递。

(3) 若满足收敛条件，即得到最优解，输出最优的可再生能源选址定容以及配电网的改造方案。

(4) 不满足收敛条件，用下层结果对和声记忆库进行更新，更新后传递至上层模型，继续进行第二步。

5 算例分析

本文以山东电网某市的配电网真实数据为例进行分析。地理空间按照纬度0.5°、经度0.67°，时间按照1 h划分时空地理网格，并根据单位风光容量出力序列，得到某地风电机组和光伏发电出力曲线如图5、图6所示。

图5 风电机组出力曲线图

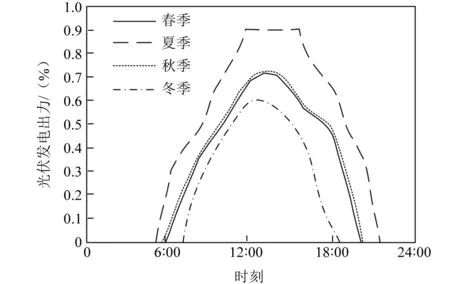
图6 光伏发电出力曲线图

给定可再生能源渗透率λL，通过第2节中的模型完成可再生能源选址与定容的初步规划，并用初步规划方案和网架信息生成初始化和声记忆库。

然后进行分区规划。该市配电网可按照变电站分为A1、A2共2个子区，配电网改造成本约束为1 000万元，降损节能目标为2%。根据历史线损情况，完成各分区及改造投资约束，如表1所示。

表1 各分区及方案投资约束

网损费用通过以下函数表示：

C=[(Pl+PCu)×6 000+PFe×8 760]×a

(22)

式中：a为单位电价，取0.6 元/(kWh)。

下层模型对线路改造(P1)、变压器改造(P2)、无功补偿(P3)和优化电压(P4)进行综合改造优化，并更新和声记忆库，得到新的可再生能源规划方案与网架信息。通过上下层模型迭代至收敛得到不同渗透率下的节能效果，如表2所示。

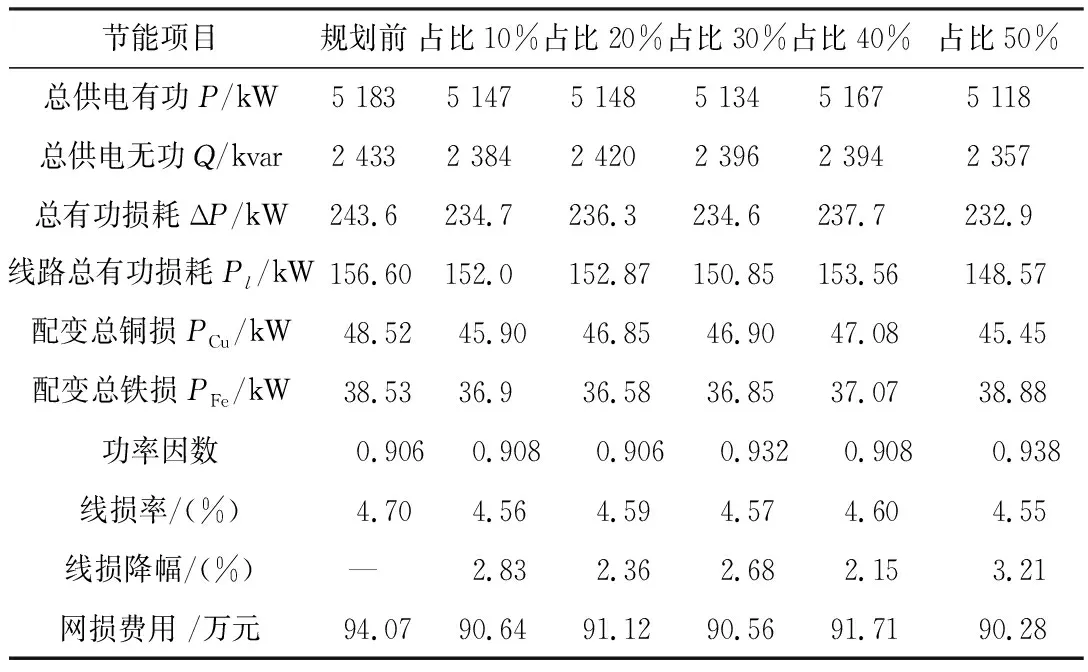
表2 不同渗透率下配电网的综合节能效果

表3 风电和光伏发电成本参数

表4所示为不同可再生能源渗透率下的整体投资成本及节能效益对比。结果显示，虽然在不同渗透率规划时，可再生能源的选址与定容影响了配电网的潮流分布，但是通过双层模型的相互迭代，配合快速高效的和声算法，所得结果均达到了降损2%的要求。综上，本文所提方法具有可行性，可为新增可再生能源寻址定容及其所在的区域配电网规划提供一定指导。

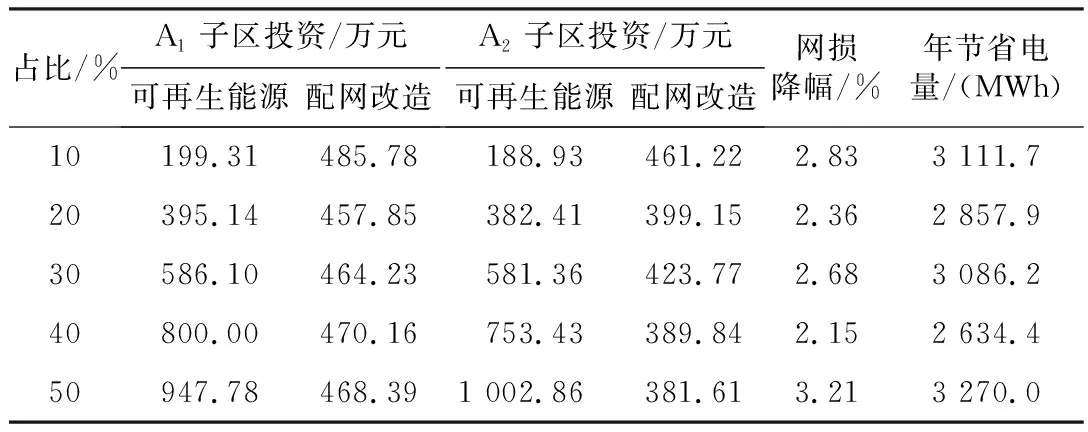
表4 不同渗透率下的规划投资及节能效益

6 结束语

本文提出的计及高渗透可再生能源接入的配电网节能规划方法，作用在于对逐步高渗透的配电网节能进行整体规划。建立的双层模型通过上下层相互反馈迭代，实现可再生能源规划及配电网节能改造方案的整体寻优，达到了投资成本最小和节能效益最优的目的。算例结果表明，本文所提规划方法有利于提高配电网整体规划决策水平，具有一定的实际应用价值。