基于KM-RF算法的电力系统暂态稳定评估

张哲， 李升， 王徐彬

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

随着电力系统的不断发展，新能源并网规模在不断扩大，电网机构变得更加复杂，电力系统的安全稳定运行面临着更加严峻的挑战[1]，电力系统在发生故障后导致暂态失稳的可能性也在增加。因此，如何快速、准确地评估电力系统的稳定状况就是一个亟需解决的问题。

对暂态稳定进行评估的方法主要有时域仿真法、能量函数法以及人工智能法。传统的时域仿真法计算量比较大，无法满足在线应用的需要；能量函数法计算速度较快，但是难以应用于大规模的复杂系统当中[2]。利用人工智能算法对电力系统的暂态稳定状况进行评估兼具时域仿真法和机器学习的优势，具备速度快、准确率高等优点，目前已在电力系统的实时评估中得到广泛运用。

文献[3]提出了安全域的概念，并使用多支持向量机综合进行暂态稳定评估。文献[4]用XGBoost算法进行暂态稳定评估，并引入了Logistic函数来提高评估模型的可靠程度。文献[5]基于主动学习，能够有效降低离线仿真的时间。文献[6]采用半监督学习的方式，减少冗余信息，提高数据的利用率。此外，还有学者将深度学习算法[7]引入到暂态稳定评估当中，主要体现在特征提取方面。然而，现有的诸多方法在提升准确率、数据不平衡处理等问题依然存在困难。

在现有研究基础上，本文提出了一种基于K-means和随机森林组合算法(KM-RF)的暂态稳定评估方法。首先，在系统发生故障的各个阶段选取能够凸显暂态特性的特征量组成原始输入特征集；然后，使用Z-Score规一化和皮尔逊相关系数法对原始样本集进行预处理，通过K-means算法来解决数据不平衡问题，采用随机森林算法并进行暂态稳定预测；最后在新英格兰10机39节点标准模型中验证了本文所提方法的有效性。

1 基本理论

1.1 随机森林原理

假设某个随进森林是由k棵CART决策树[h(X,θk),k=1,2,3,…]构成，边缘函数如式(1)所示。

(1)

式中：X为输入向量，最多包含J种不同的类别；j为J种类别中的某一类；θk相互独立且同分布的随机向量;Y为正确的分类向量；I(.)为指示函数;ak为求取平均值的函数。

随机森林的泛化误差如式(2)所示

Pe=PX,Y[K(X,Y)<0]

(2)

式中：P(X,Y)为对给定输入变量X的分类错误率函数;X，Y为概率定义空间。

当森林中决策树数目较大时，随机森林泛化误差的上界如式(3)所示

(3)

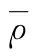
1.2 组合优化算法

先使用K-means聚类算法将同一个类标签下的数据分解成Ki个簇，其中i是指原始数据集中的标签数，然后再使用随机森林算法利用已分解的数据集进行分类预测。

整个过程需要对4个参数进行调参：簇数Ki(K1,K2)，决策树个数(n_estimators)，每棵决策树所选择的分类特征数(max_features)。

对于一个特定的数据集X，类别为Y，假设这Y个类中有m个子类标签。定义一个特征向量V代表整个模型需要优化的参数，如式(4)所示。

(4)

式中：yi∈Y；ki为指第i个类被分解成k个子类。在这个模型中不仅要确定簇数，还要确定哪个类将会被分解。

2 评估模型

2.1 特征量选取

针对故障开始时刻和切除时刻两种状态选取具有代表性的特征量[8-9]。故障开始时刻的特征量能够反映瞬时功率平衡状态被打破的程度以及对暂态稳定的影响；故障切除时刻的特征量能够反映故障持续期间不平衡能量的集聚给系统带来的冲击。选取的特征量均为系统特征，而不是单机特征，能够避免因系统规模扩大而带来的特征量维数的急剧增加。然后，对原始特征集进行Z-score归一化和相关性分析。可以将不同的特征量转化为同一个数量级，从而避免某些特征量由于数量级之间差距过大而无法发挥作用。删除相关性过高的特征量以提升模型效率。

2.2 建模过程

模型建模过程如图1所示：①利用时域仿真法获得原始特征集；②在数据预处理阶段对特征集进行归一化处理，并分析特征量的相关性；③使用K-means聚类算法对样本集进行类分解，并进行参数调节；④在分解后的数据集的基础上，调节随机森林的参数；⑤模型评估并引入指标进行评价。

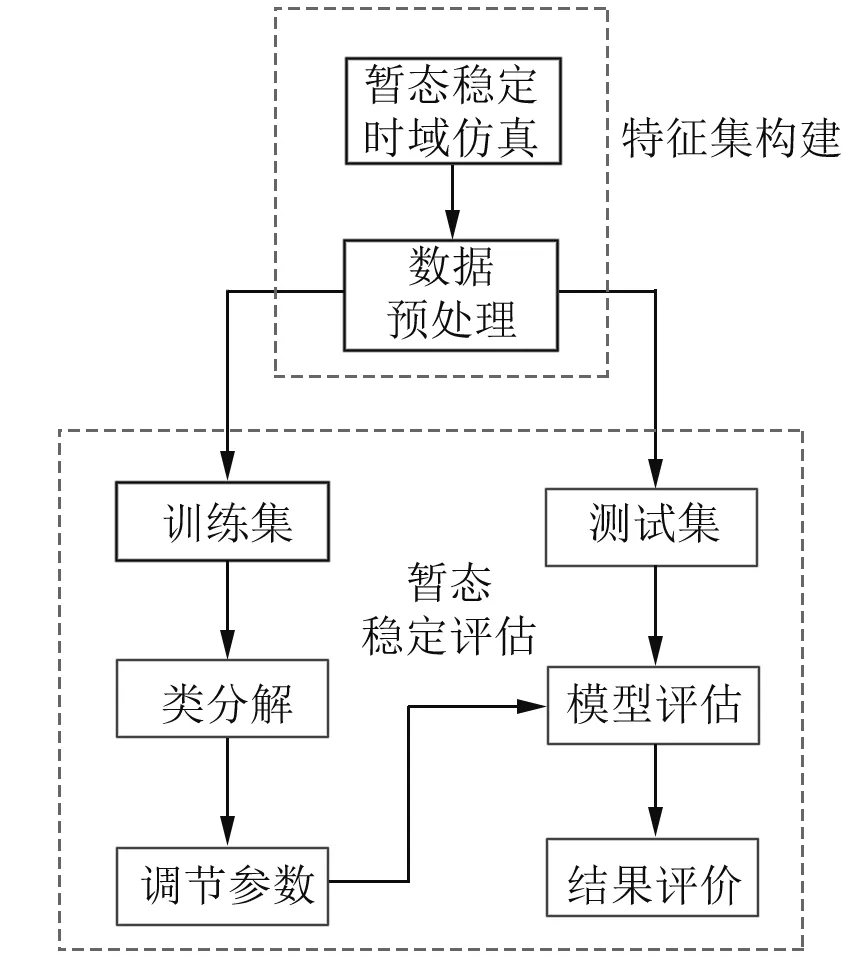
图1 评估模型流程图

3 仿真算例及结果分析

3.1 数据集生成

以新英格兰10机39节点系统进行算例分析，利用MATLAB中的工具箱PSAT进行仿真，采集故障数据。在80%、90%、100%、110%和120%标准负荷水平下，随机设置4种不同的发电机出力，设置每条母线处发生一个三相短路故障，共计39处故障。故障切除时间为0.2 s，数据采样周期为0.01 s，共生成780(39×5×4)组样本，以系统中任意两台同步发电机相对功角之差是否大于360度来判断系统的暂态稳定性，将所有的样本集存储在矩阵当中，矩阵的每一行分别代表一组样本数据。

3.2 评价指标

在通常情况下，模型的效果与精确度成正比。但是，精确度忽略了不平衡样本带来的影响，反映的仅仅是数据集的总体预测精度。混淆矩阵(confusionmatrix)能够很好地评估出模型的效果，如表1所示。

表1 混淆矩阵

为了更精细地判断评估模型的性能，引入误报率(false positive rate, FPR)、命中率(true positive rate, TPR)、准确率(accuracy, ACC)以及KAPPA系数，计算方法如式(5)～式(8)所示，其中KAPPA系数值越高则代表模型整体性能越好。

(5)

(6)

(7)

(8)

式中:P0为准确率；Pe为一个函数。在二分类问题中，如果每类样本真实个数为A1、A2，预测所得每类样本的个数为B1、B2，总样本数为N，Pe的计算方法如式(9)所示。

(9)

3.3 测试结果

试验结果如表2所示，当n_estimators=556，max_features=12，K1=1，K2=2时，效果最好。整体来看，ACC均值为0.91，KAPPA系数均值为0.82，TPR>0.91，FPR<0.17。

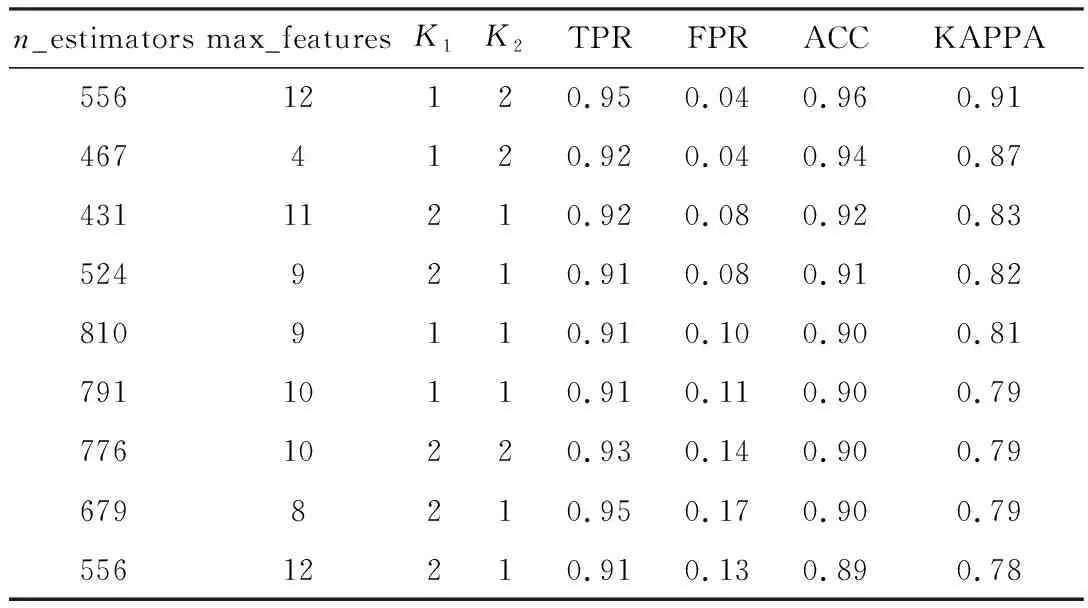
表2 KM-RF测试结果表

在相同的特征集数据、相同的数据处理方式情况下，分别使用KM-RF、DT、RF、SVM进行预测，结果如图2所示。通过对比，可以发现KM-RF模型在各性能指标上也有明显优势，准确率、命中率以及KAPPA系数值最高，误报率最低。

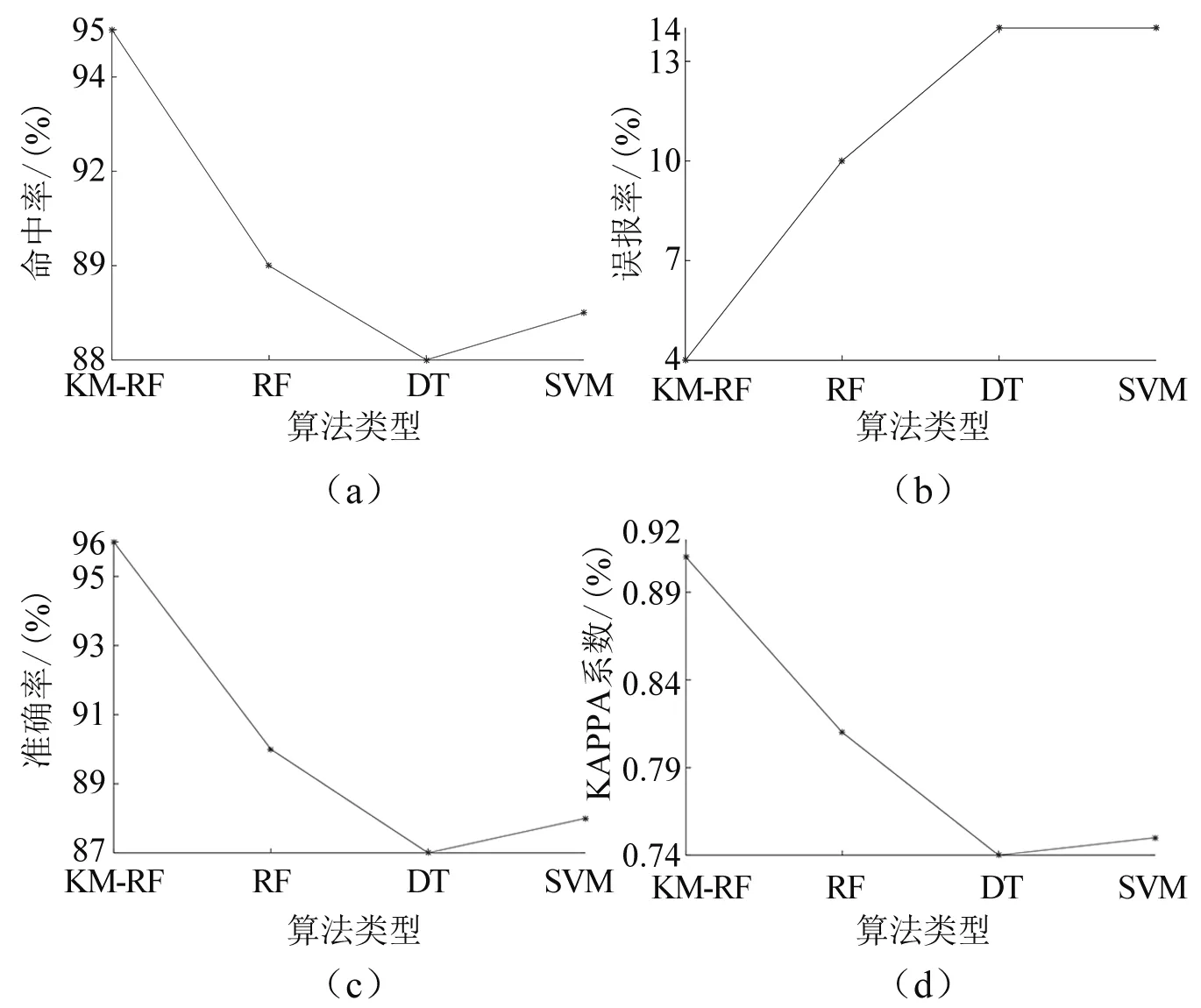
图2 各算法结果比较图

4 结束语

(1) 通过对发电机动态特性分析，所构建的特征集能够较为全面地反映暂态稳定的特性，提升了评估结果的准确性。通过对特征集进行Z-score归一化处理以及皮尔逊相关性分析，避免了部分特征量无法发挥作用的问题并对相关性较高的特征量进行了筛选，提高了模型的效率和准确性。

(2) 使用K-means进行类分解，很好地解决了数据不平衡的问题，提升了整体性能。随机森林算法分类精度高，不容易过拟合且泛化能力较强，基于此的组合算法能够较好地处理暂态稳定评估问题，通过与决策树、随机森林以及支持向量机的评估结果进行比较，在各个指标上都具备明显优势。