基于随机矩阵理论的地下电缆异常检测方法研究
段晨东, 张伟, 代杰
(长安大学 电子与控制工程学院,陕西 西安 710064)
0 引 言
地下电缆的异常状态运行不仅影响供电电能质量,还会对输电线路元器件和用电设备造成损坏,及时准确地发现地下电缆异常状态尤为重要[1]。
地下电缆检修复杂,难以及时发现异常。文献[2]提出阻抗和FFT结合的方法,从频率响应的角度识别地下电缆的异常,但受线路元器件和非线性负载的影响,频率响应的方法抗干扰能力差。文献[3]提出应用S变换和SVM来识别存在异常的地下电缆,但该方法需要较大的数据集,且机器学习方法对信号质量要求高,运算时间较长。
文献[4]和文献[5]提出纯数据驱动的信号处理方法——随机矩阵理论,该方法具有不受数据模型限制的优势。文献[6]和文献[7]将随机矩阵理论引入电力系统异常检测领域。应用随机矩阵理论识别异常数据从而实现异常检测,当前文献普遍采用平均谱半径作评价指标,且一般应用于配电网仿真模型异常,分析效果较好。
考虑地下电缆监测数据受负载和环境影响波动大,单一指标误判率高等问题。本文提出基于随机矩阵理论(random matrix theory, RMT)和奇异值分解(singular value decomposition, SVD)构造融合指标的地下电缆异常检测方法。工程验证结果表明,该融合指标与传统指标相比,受信号正常波动的干扰较小,误判率低,具有更好的异常表征效果。
1 地下电缆异常检测与随机矩阵理论
1.1 地下电缆异常识别
电力设备发生异常时,电流信号相较于电压信号对异常更加敏感,因此选择电流信号作为地下电缆异常识别依据。正常情况下,电流信号由供电工频分量、非线性元件和负载引起的谐波分量以及采集设备引起的随机噪声分量组成,异常出现时,电流信号中会出现异常成分,式(1)和式(2)分别表示正常和异常信号数学模型。
(1)
i1(t)=i0(t)+a(t)
(2)
式中:Ak为电流峰值;k为谐波次数;fr为电流基频;φk为k次谐波的起始相位;n(t)为随机噪声。当系统中含有异常事件a(t)时,系统的运行机制和原有特性将会破坏,采集的系统数据不满足原有的统计分布规律。
1.2 随机矩阵理论
随机矩阵理论反映了系统内部在各种相互作用下的一种平均性质,偏离随机矩阵理论反映出系统内部含有异常信号引起的特殊属性,这为异常检测提供了理论支撑。随机矩阵理论体系中相对成熟的理论有Marchenko-Pastur(M-P)定律和单环定律。
1.2.1 M-P定律
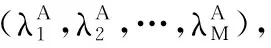
(3)

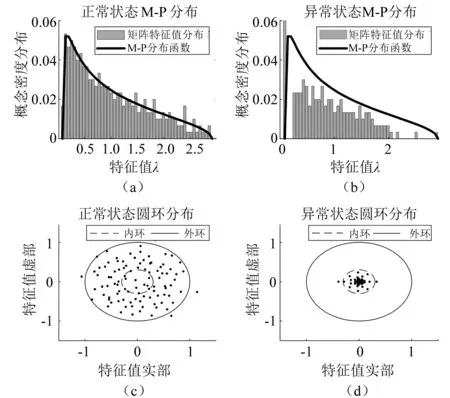
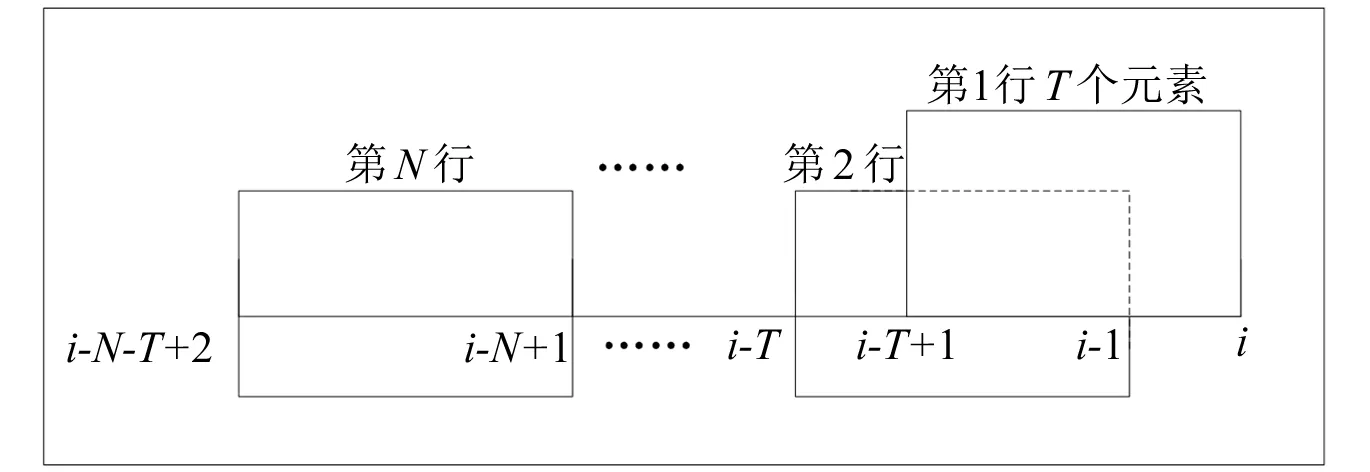
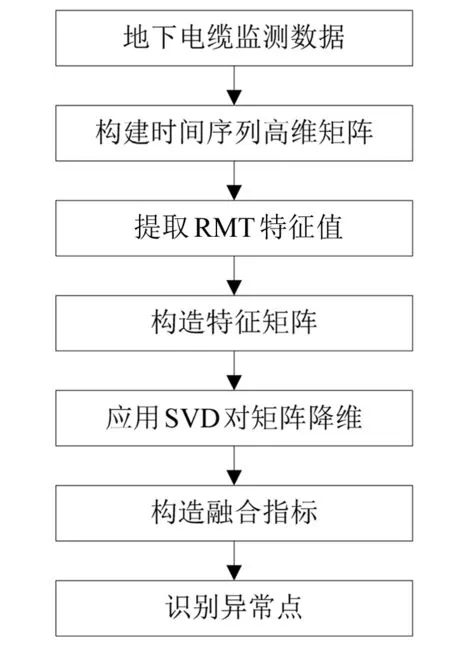
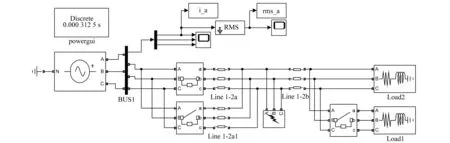
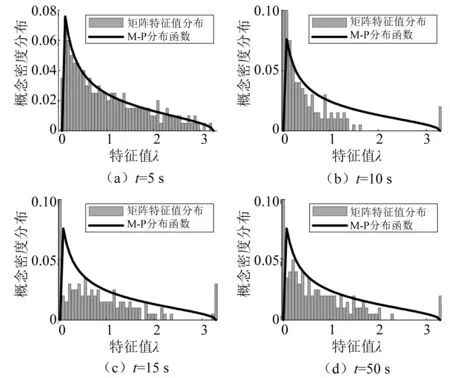
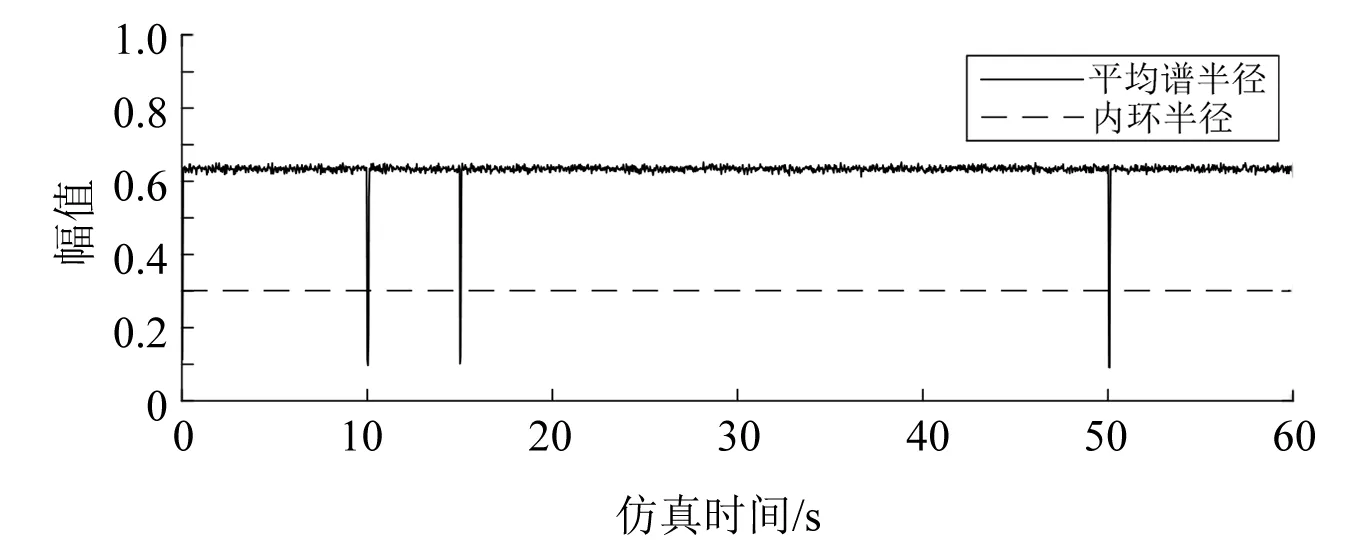
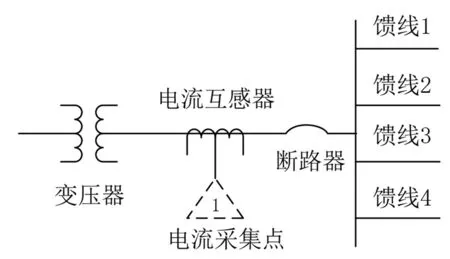
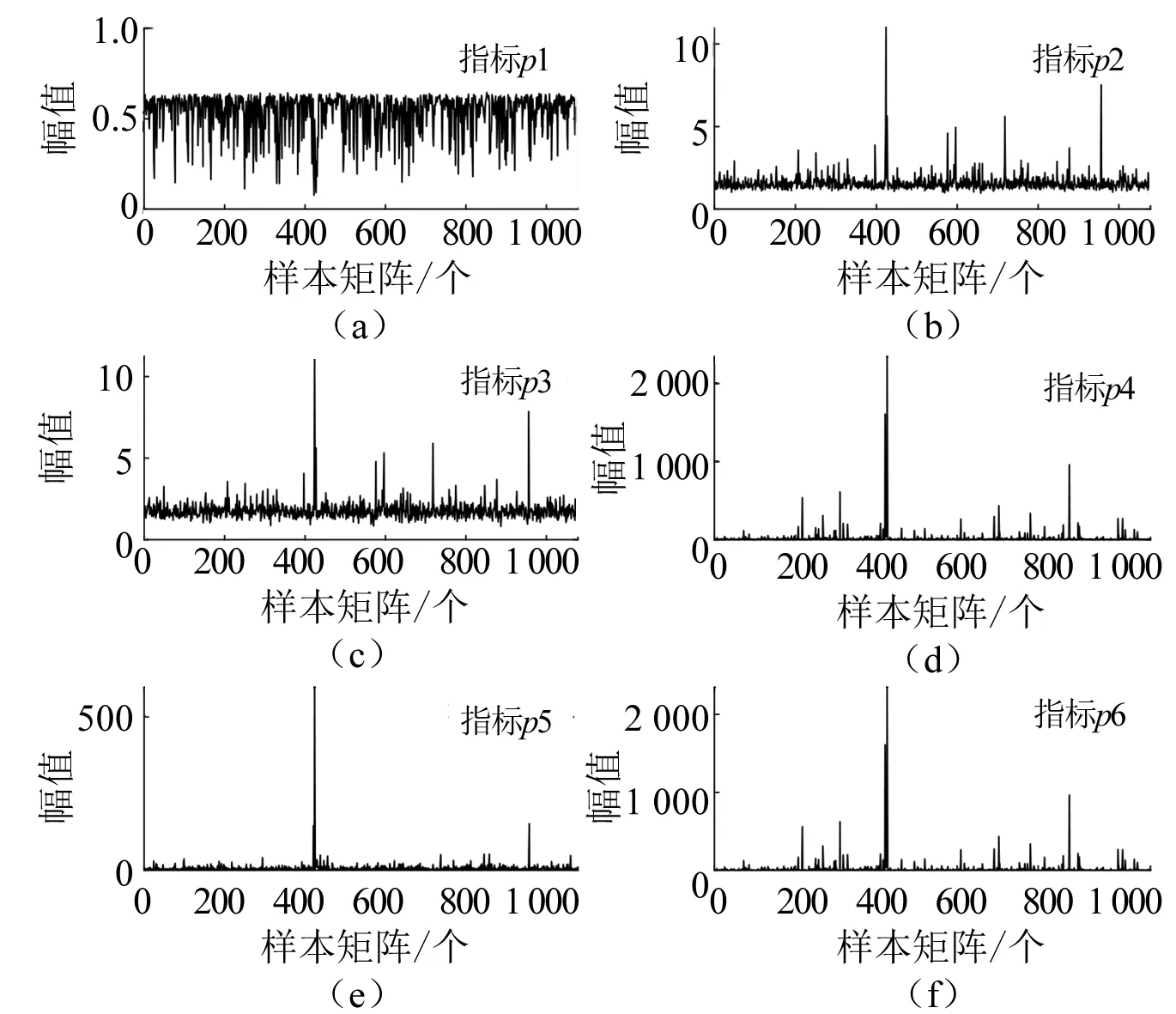
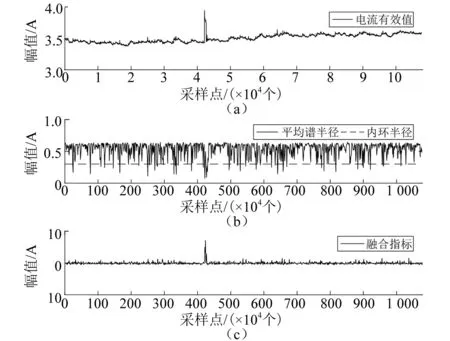
对于矩阵元素独立同分布且满足μ(x)=0,σ2(x)=d分布的非方阵XN×T(N (4) 式中:d为矩阵方差;T为矩阵X的列数;XH为矩阵X的共轭转置矩阵。 由M-P定律可知,样本协方差矩阵S的经验谱分布满足如下概率密度函数: (5) 1.2.2 单环定律 对于矩阵元素独立同分布且满足μ(x)=0,σ2(x)=d分布的非方阵XN×T(N (6) 式中:U为哈尔酉矩阵。定义其矩阵积为: (7) 式中:L为奇异值等价矩阵个数。对矩阵Z进行归一化处理后,矩阵有N个复数特征值,由圆环定律有,其特征值分布满足式(8)所示概率密度函数。 (8) 图1反映了正常和异常信号构造高维矩阵时特征值分布的对比情况。 图1 正常状态与异常状态的特征值分布 对地下电缆监测数据按时间序列构建高维矩阵,图2所示为ti时刻N×T高维矩阵构建示意图。通过随机矩阵理论提取每个高维矩阵的特征值并统计其特征指标,按时间序列构造特征指标矩阵。 图2 高维矩阵构建示意图 应用奇异值分解对特征值矩阵进行降维并构造融合指标,流程如下。 (1) 特征指标矩阵Pn×m(n为构建的高维矩阵个数,m为每个矩阵特征指标个数)按式(9)进行奇异值分解[8]。 (9) 式中:Un×n为左奇异矩阵;Vm×m为右奇异矩阵;λn×m为奇异值矩阵。 (2) 利用式(10)计算各奇异值的贡献率。 (10) 式中:si为第i个奇异值。 (11) 图3 RMT_SVD算法流程图 本文基于地下电缆的分布参数模型搭建如图4所示的10 kV/50 Hz地下电缆输电线路。仿真总时长设置为60 s,电缆异常情况设置安排如表1所示。 图4 仿真模型 表1 仿真设置 每0.02 s记录一次电流数据,则样本矩阵S∈c1×3 000。本文设定N=100,T=110采用移动分割窗口对样本矩阵S构造间序列高维矩阵X(i)∈c100×100(i=1,2,…)。应用随机矩阵理论的M-P定律和单环定律对矩阵X(i)特征值统计。 图5为仿真过程中几个代表时间点的高维矩阵特征值分布情况。 图5 t=5 s、10 s、15 s、50 s M-P分布 图5中,在t=5 s时,电缆正常运行,特征值的经验谱分布近似满足M-P分布曲线;t=10 s、15 s、50 s时,电缆输电系统均发生异常,此时构造的高维矩阵特征值分布不满足M-P分布曲线。 图6为随时间序列变化的高维矩阵特征值平均谱半径统计图。平均谱半径计算公式为: 图6 平均谱半径统计图 (12) 式中:λi为圆环定律计算得到的第i个特征值。 由式(8)计算得到圆环的内环半径和外环半径分别为0.3和1。正常情况下,高维矩阵的特征值的平均谱半径稳定在0.63;t=10 s、15 s、50 s时,高维矩阵的特征值平均谱半径明显低于内环半径。 仿真结果验证了随机矩阵理论对信号异常领域应用的可行性,信号存在异常时,高维矩阵的性质发生变化,特征值分布不满足随机矩阵理论。 本文采用8 kV交联聚乙烯(XLPE)地下电缆监测A相电流数据[9],监测点示意图如图7所示。电流频率60 Hz,采样频率3 840 Hz。 图7 试验数据监测点示意图 应用随机矩阵理论的单环定律对矩阵X∈cN×T进行特征值计算,λi(i=1,2,…,N)为矩阵的N个特征值,利用表2所示的公式构造了6个特征指标,式中max(·)、min(·)、mid(·)分别表示最大值、最小值和中位数。 表2 特征指标构造公式 ti时刻特征指标向量p(i)∈c1×6(i=1,2,…,n),将计算得到的特征指标向量按时间顺序构成多指标矩阵Pn×6,即: P=[p(1),p(2),…,p(i)] (13) 应用SVD对矩阵P进行降维,选择累计贡献率达到90%的前几个特征指标构造新的特征指标矩阵,求取新的特征指标的平均值作为融合指标。 如图8所示为某一时间段A相电流波形。为了得到近似满足随机分布的相对平稳的数据集,每50个周期记录一次电流数据用于构建矩阵。基于单环定律的特征值构造表2列出的6个特征指标,6个特征指标随时间变化趋势如图9所示。其中,指标p1为随机矩阵理论常用指标平均光谱半径,将指标p1和SVD处理后获得的融合指标的变化与电流有效值在图10中进行对比。 图8 电流监测信号 图9 特征指标趋势图 图10 指标对比图 图9中,6个指标幅值波动较大,无法用于区别正常状态和异常状态。由图10可以看出,受负载和输电线路影响,地下电缆在正常运行时电流有效值并不是保持不变,其有效值在3.5 A附近波动,在电流异常点其有效值高达3.9 A。此时,平均光谱半径远低于内环半径,可以判断电缆在此时存在异常,但受电流波动影响,在电缆正常运行时也会出现平均谱半径低于内环半径的现象,造成误判。本文构造的融合指标在异常点的幅值异常突出,在正常状态下构造的矩阵的融合特征值具有较好的稳定性,相较于平均谱半径具有更好的异常表征效果。 用仿真电流采样点构建高维矩阵发现随机矩阵理论对模拟信号的异常点具有较好的识别效果。 地下电缆在运行过程中,电流会受负载影响出现一定范围内的正常波动,随机矩阵的传统单一指标对电流的波动较为敏感,容易出现误判的情况。本文提出的RMT_SVD理论利用奇异值分解构建随机矩阵的融合指标用于识别地下电缆电流异常信号,研究结果表明,该融合指标在实际监测中抗干扰能力较强,具有更好的异常识别效果。
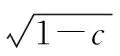
2 基于RMT_SVD的地下电缆异常检测
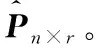
3 试验

4 工程应用
4.1 特征指标

4.2 结果分析
5 结束语

