基于三维虚拟现实技术的电力数据可视化分析

程鹏

(国网廊坊供电公司，河北 廊坊 065000)

0 引 言

大数据挖掘技术目前已经在电网企业及电力系统的运行管理中广泛应用。但是如何利用大数据技术来深度挖掘这些数据的内在规律以及通过可视化技术来实现更好的电力系统管理是当前要解决的具有挑战性的问题。将可视化技术应用到电力大数据挖掘之中，能够突破传统二维图表在可视化及直观性上的局限性，解决传统可视化方法出现的重叠及密集区域[1-3]。为了能够更好展现电力设备的地理空间特性及设备的运行状态，应当考虑引入数据挖掘智能算法，实现电力大数据的全景状态数据展现，深度挖掘不同空间位置数据之间的相互关系。

1 三维场景模型可视化优化重建

1.1 算法优化设计

为了能够获得更快的刷新速度以及更快的场景绘制速度，需要利用场景漫游以及快速人际交互等多种技术[4]。在电力设备的三维模型构建中，由于这些电力设备大部分都具有多线圈结构且表面局部曲率很大，因而不能够过度简化，否则无法实现对场景重绘的目的效果[5-6]。在此情况下，考虑引入LOD(levels of detail)方法进行模型构建过程的简化，提高场景绘制的速度。首先分析模型结构，采用三角网格(mesh)开展数学描述，即M=(K,V)。对模型的简化，并非是进行E的简化，而是要逐渐过渡到E，需要对E进行量化分析，从而确定其重要程度。可以利用能量函数思想进行模型简化的逼近程度，并不断修正顶点数量变化权重。利用能量函数进行模型构建的时候，难以有理想减面效果，算法复杂，执行率低，因而并不适用于场景复杂的变电站中。

E(K,V)=Edist(K,V)+Erep(K,V)+Fspring(K,V)

(1)

式中:E为三角网格的连接顶点基本元素，实际模型中替换为M=(E,V)，表示三角网格模型;K,V分别为三个连接顶点基本元素和顶点；Edist为距离能量;Espring为弹性能量;Erep为代表性能量。因而提出LOD算法融入能量函数思想，结合统计方法加权进行K值重要性量化，对于边E影响因子A有：

(2)

式中:W为边E的影响因子权重函数；n为影响因子数量；Fi为所有特征边标识；Ai为i种不同的影响因子;wi为影响因子对应的权重 。在进行电力大数据可视化过程中，最主要是进行电力设备的构建，因而不能够过度简化[7]。综合考虑之下，E选取影响因子A1、A2、A3、A4，分别对应的是边长L、特征边标识F、两侧三角形面积S和曲率C。

设边E(V1，V2)两侧三角形如图1中所示，四个点的坐标分别为V1(x1,y1,z1)、V2(x2，y2,z2)、V3(x3,y3,z2)、V4(x4,y4,z4)，则有：

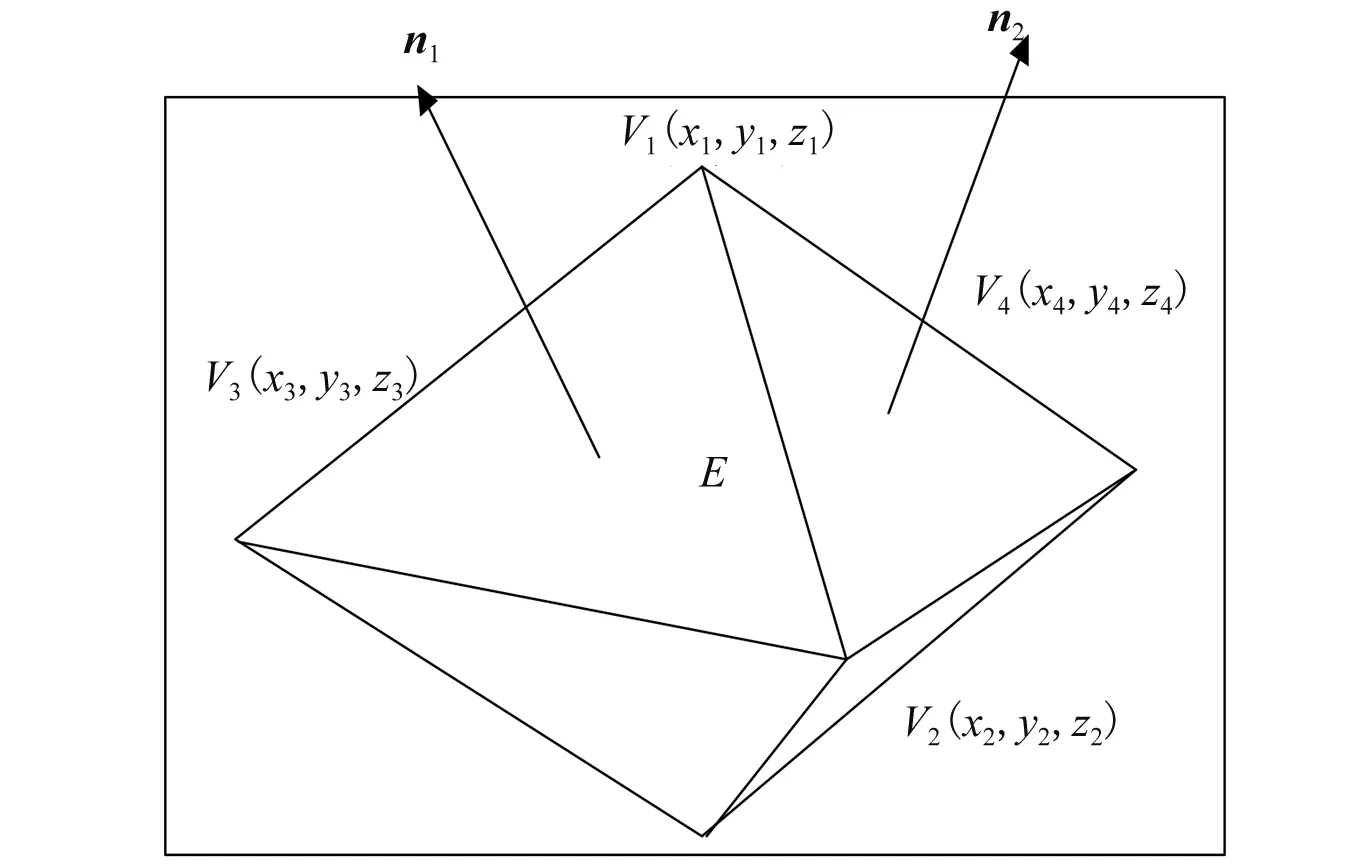
图1 周围相关顶点及法向量示意图

(3)

(4)

(5)

C=cos-1n1·n2=

(6)

式中:F、L、S、C分别为特征边标识、边长、两侧三角形面积和曲率(后同)；n1、n2为图1中的两个方向法向量。利用权重函数E=f(E)对影响因子加权计算，进一步设计基本权重函数。

W0=w1·L+w2·F+w3·S+w4·|C|

(7)

式中:w1、w2、w3、w4为L、F、S和|C|对应的权重系数，其中C的值域区间为[0,π]。L、S值域是难以确定的，如果单纯直接使用L、S原始值进行计算，可能会导致最终产生较大的误差，因而需要对影响因子进行均衡化处理，使其能够处于同一尺度空间中。将L、F、S值域线性映射至[0,π]区间中，设：

(8)

EFj=π·Fj

(9)

(10)

由此能够得到均衡值域的权重函数计算公式：

W=w1·EL+w2·EF+w3·ES+w4·|C|

(11)

式中:C为曲率，值域为[0，π]。为了进行模型简化，令w1=σEL，w3=σES，w4=σC，w2=α。对于给定任意边E，可以得到权重函数方程为：

W=σEL·EL+α·EF+σES·ES+σC·|C|

(12)

由此可以保证影响因子贡献比例的均衡，完善边E的贡献值。将其应用到电力可视化模型构建时，可以对权重系数按照线性缩放的原则进行调整。

1.2 模型简化及重建

利用式(10)可以计算出模型中每个E贡献值，然而还需要进一步完成LOD计算方法的过程完善，还需要进一步定义模型构建过程中模型顶点列表的变换确认简化比例，完成不同比例参数的分配等。在对E进行约减时，为了填补删除后可能留下的缝隙，操作需要遍历三角网格模型，因而消耗大量的计算时间。在此采用收缩方式代替删除方式，对E进行收缩变换。

E(V1,V2)→E(V1,V3)

(13)

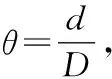
1.3 仿真运算

将简化仿真算法应用于某个变电站数据分析系统之中，开展变电站的场景优化，对其测试算法效率和效果进行分析。经过初步的仿真模拟，对于不同简化比例参数θ为0、70%、85%，对应的场景优化效果效率曲线如图2及表1所示。从图2及表1可以看出，当处于初始化状态时为0，对应的FPS(frames per second)=3.8帧/s；当简化比例为70%时，FPS上升为15.4帧/s，对应的细节基本上没有损失，能够保持案例设备的完整性，实现最好的优化效果；当简化比例为85%时，损失了较多细节，即便仍能够保持有大致的设备外形，但是精度上有着显著的降低，此时的FPS为18.1帧/s，对应的连续帧率阈值为24 FPS，能够满足人机交互及变电站的场景漫游需要。

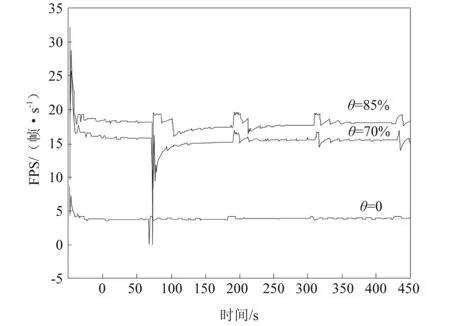
图2 场景优化效率曲线图

表1 场景绘制效率表

整体分析可以看出，当简化比例参数在85%以上时，模型陷入扁平化，可能导致三体塌陷成为二维面，最终产生体积信息的损失，因而需要进一步提升扁平化阈值。

2 基于数据挖掘技术的可视化算法优化

2.1 数据挖据技术分析

利用Amdahl定律，采用并行方式加快算法，运行速度存在极限，不能实现无限提高。具体计算公式为：

(14)

式中:S、a、n分别为加速比、串行比例和并行节点数。当a无限趋近于0时，才能够实现n加速比。结合CUDA(computer unified device architecture)三层编程模型，可以将BP神经网络算法划分为三个层次：第一层次是每个Grid对应的单个神经网络计算任务；第二层次是Block对上层节点的计算任务；第三层次是Thread对应的节点计算任务。对应的并行层次计算模式如图3中所示。

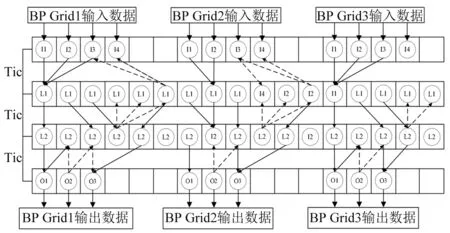
图3 BP神经网络的并行层次计算模式

2.2 算法仿真训练

为了进行基于BP神经网络改进后的并行算法的效果分析，此次选取95台主变压器的相关监测数据来进行具体的仿真分析。在这个仿真体系中，每一台变压器就相当于一个神经网络，由此分别进行BP及BP Grid算法效率的对比分析，结果如表2所示。

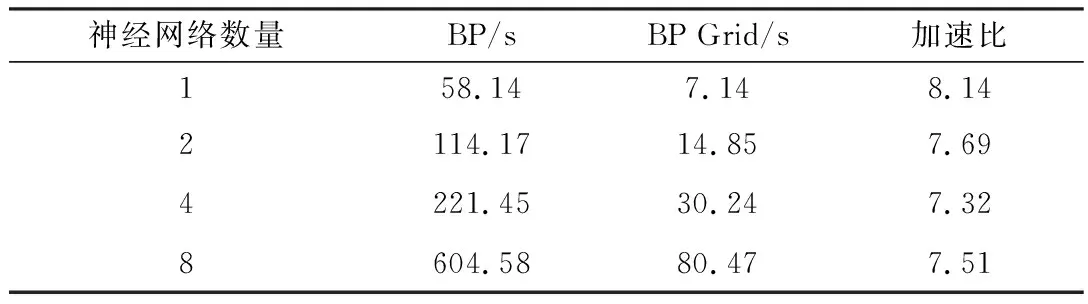
表2 BP Grid算法的加速比

从表2可以看出，对于不融入并行算法大数据技术时，整个算法的效率非常低，单台变压器所需要消耗的时间要达到58.14 s，消耗的时间过多，难以达到实用要求。而融入了BP神经网络算法后，BP Grid算法单台变压器的消耗时间为7.14 s，与单纯的神经网络训练时间相比加速比为8.14。进一步分析可以看出，神经网络数量为1、2、4、8时，对应的加速比分别为8.14、7.69、7.32、7.51。

3 电力数据三维可视化

利用此次提出的可视化方法对三维场景的结果进行可视化展示。为了更好实现可视化的展现，设计出一种三维平行坐标图，用以展开时间序列数据对应的时间维度，能够将多个时间点数据同时排列其中。为了缓解空间可能出现的紧促感，需要将曲线排列在三维空间之中。在三维空间之中，可以利用视点位置的改变以及场景漫游等解决二维平行坐标图中可能出现的遮挡问题。根据此次可测试数据得到的结果集进行可视化展现，具体如图4～图7所示。

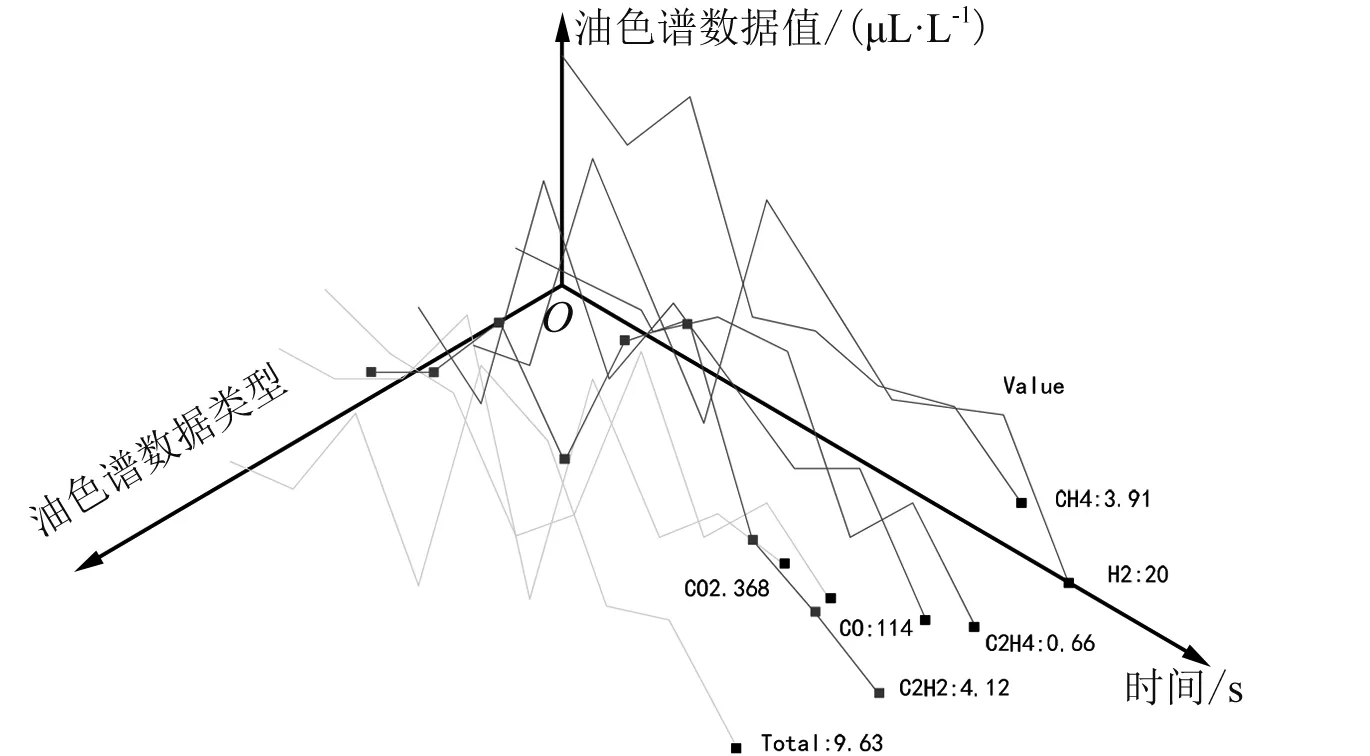
图4 三维平行坐标图(1)

图5 三维平行坐标图(2)

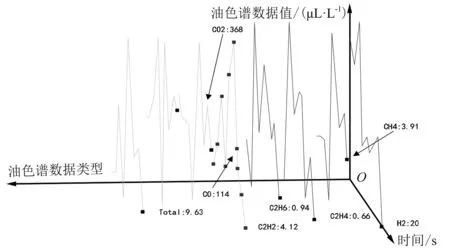
图6 三维平行坐标图(3)

图7 三维平行坐标图(4)

数据集分析的结果可视化展现在图8中，图中的“★”为存在异常数据，黑色点为最近数据采集结果的维度数值。将三维场景的实现和数据结合起来，能够增强人机交互效率，让人们更好了解到数据背后隐藏的规律。

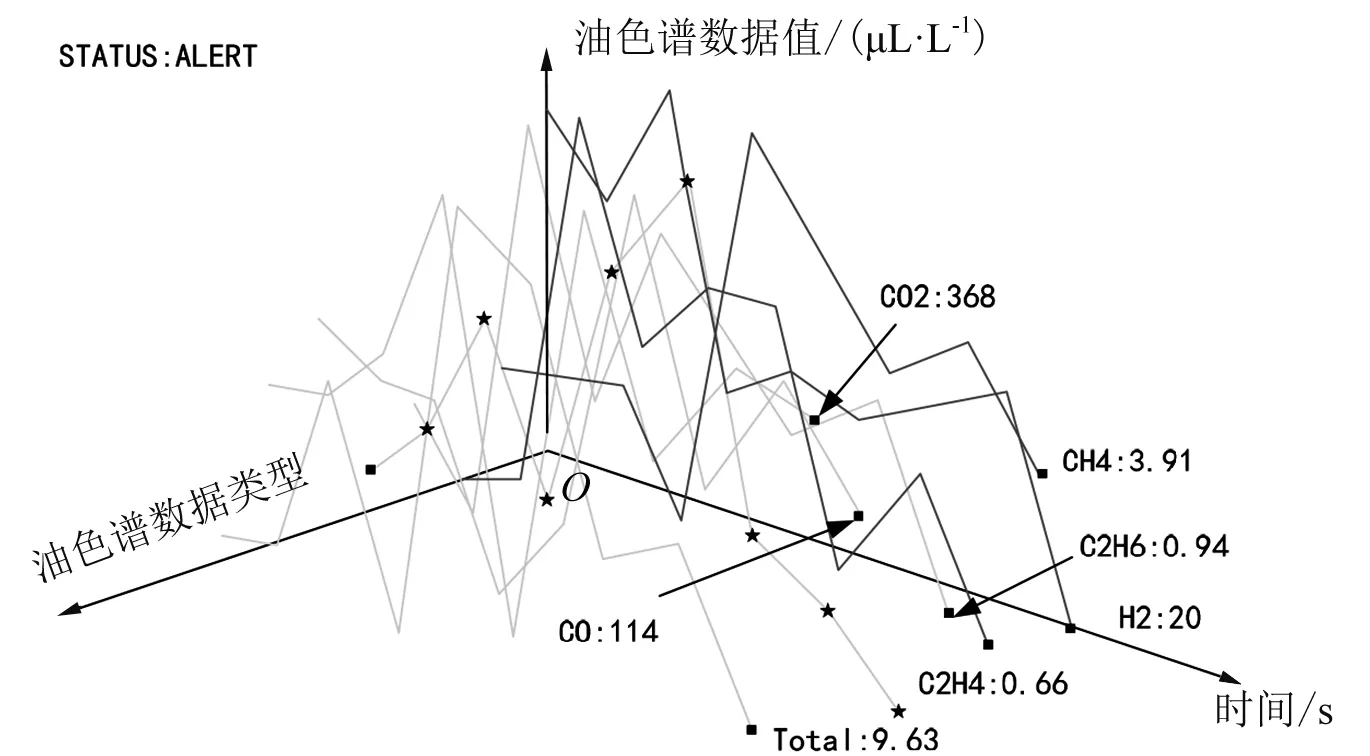
图8 变电站可视化三维虚拟现实场景

综合分析可以看出，并行化BP神经网络的BP Grid算法能够对输入的时间序列数据实现高效快速的神经网络训练。通过和传统可视化的对比分析可以看出，BP神经网络输出结果可以让用户在地理空间上实现快速的定位，便于其更好地理解数据。通过可视化分析方式，用户能够快速定位数据源，基于三维场景辅助可视化方式进行异常数据点的查找，有利于提高人机交互效率。

4 结束语

本文整合了大数据技术和可视化分析模型，通过数据挖掘并行优化算法，实现渐进、动态和无损的模型简化重建。通过仿真试验数据的快速可视化分析模型构建可以看出，此次的分析模型能够满足电力企业的大数据业务需求，便于用户对数据的人机交互需求和理解，极大提升了人机交互效率。当采用多分辨率快速渲染方法的时候，可以在不改变电力设备外观的情况下快速实现异常设备点的定位，有助于电力系统的日常运维管理。