基于模糊PID的深海采矿机器人路径跟踪控制

毛竞航，吕海宁，杨建民，刘 磊

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 高新船舶与深海开发装备协同创新中心，上海 200240)

深海多金属结核等矿物资源的开采技术是海洋资源开发技术的最前沿，标志着一个国家开发海洋资源的综合能力和技术水平，正越来越受到社会各界的关注。

深海采矿机器人技术是深海多金属结核采矿系统的关键技术[1]，采矿作业中，采矿机器人需携带矿石收集装置和矿石输送装置覆盖式地走遍整个矿区。由于深海海泥含水率高，颗粒细小，其抗压强度及抗剪切能力弱，故采矿机器人常采用履带式行进系统。采矿机器人在海底行走时，由于海底沉积物稀软，采矿机器人极易打滑，且存在海流、地形等扰动使得采矿机器人容易偏离预定行驶路线，影响行走精度，且履带系统的非线性增加了其控制难度。

对于地面行走机器人，已经提出了多种路径跟踪方法，如follow-the-carrot方法[2]、纯跟踪方法[3-4]、向量追踪方法[5-6]等。Yeu等[7]和Yoon等[8]将跟踪算法与深海采矿机器人定位相结合，提出了深海采矿机器人的路径跟踪算法。但是，地面路径跟踪算法通常忽略打滑的情况，而深海的环境相比于陆地环境，打滑是深海采矿机器人运动控制中不可忽略的一项。李力等[9]基于采矿机器人运动学建立采用PID控制履带左右速度实现预定行走速度模型和采用模糊控制实现自动跟踪预定开采路径模型，并完成了在多种目标路径下的仿真试验，考虑了随机打滑下海底机器人的行走性能。基于运动学模型的控制算法，由于其未考虑系统输入与打滑的相互关系，容易导致由于系统输入引起的打滑问题。

随着对深海泥土力学性质研究[10-12]及软土地上履带车行驶性能研究的深入[13-15]，Hong等[16]提出了一种基于动力学模型的路径跟踪算法。Dai等[17]在RecurDyn/Track和Matlab/Simulink中建立了海底履带车联合仿真模型，提出了一种自适应模糊神经控制算法。Yeu等[18]使用改进的向量追踪路径跟踪控制算法，并通过数值模拟验证了该算法。基于动力学方程的算法有效提高了控制精度，但是其使用的打滑模型是一个根据土壤剪切应力统计值建立的模型，其打滑率在机器人运动过程中不会发生变化；而在工程实际中，由于土壤并不均匀，机器人在运动过程中土壤牵引力与打滑率之间的关系并不恒定，且牵引力对打滑率的变化敏感，打滑率的微小变化会引起牵引力的巨大变化，这容易导致实际应用中控制效果较差。为了克服运动学模型未分析打滑及动力学模型只能反应统计值的缺点，采取了动力学模型获得打滑关系指导在运动学模型中建立控制器的方式，既减弱了由于动力学模型不精确对系统的影响，又将打滑问题引入到控制算法中，实现了考虑打滑情况的采矿机器人路径跟踪。

1 采矿机器人模型

将采矿机器人的运动放在一个二维平面上以简化采矿机器人模型，因此车辆的运动可以简化为一个3自由度的运动(x,y,θ),其中，x，y表示采矿机器人的坐标。如图1所示，δ1、δ2分别为大地坐标系和车体坐标系。大地坐标系δ1的原点Oδ1可设为采矿机器人运动平面内任意点，x轴指向正东方向，y轴指向正北方向，θ以逆时针方向为正方向。车体坐标系δ2的原点Oδ2设于采矿机器人底盘形心处，x轴指向车体正前方，y轴指向车体的右侧，θ以逆时针方向为正方向。

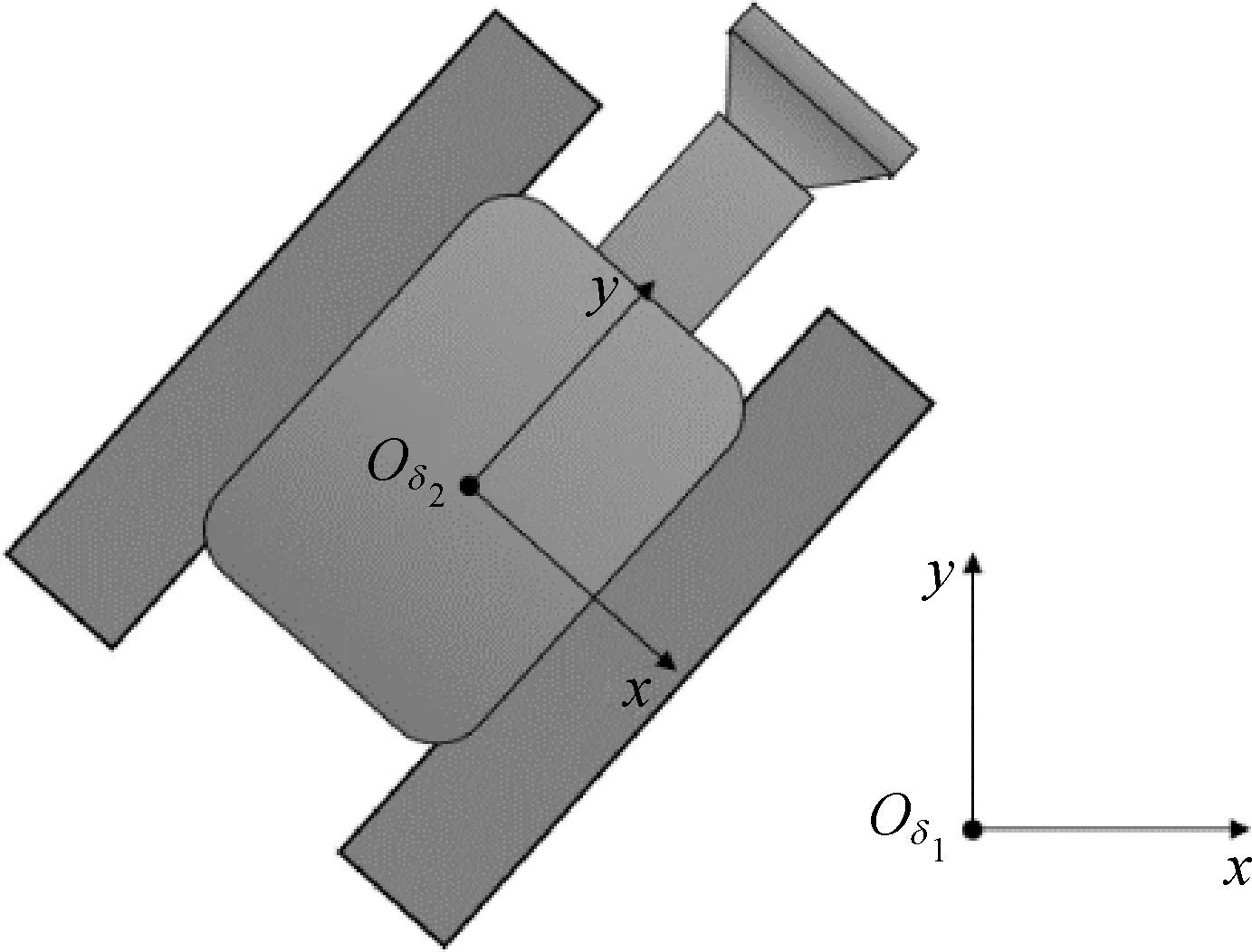
图1 采矿机器人参考系Fig. 1 Reference frame of mining robot

在两个坐标系间采矿机器人的运动转换满足：

(1)

式中：n1=[X1,Y1,θ1]为大地坐标系下采矿机器人的位置和艏向坐标，ν1=[u1,ν1,ω1]为车体坐标系下采矿机器人的运动速度角速度向量。Jθ(n1)为由坐标系δ2至坐标系δ1的转换矩阵：

(2)

采矿机器人运动学模型如图2所示，其运动学方程为：

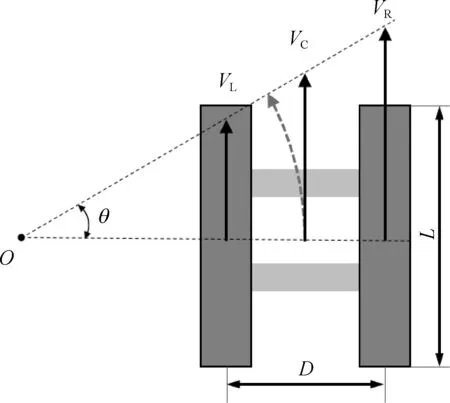
图2 采矿机器人运动学模型Fig. 2 Kinematic model of mining robot

(3)

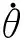
采矿机器人动力学模型如图3所示，其动力学方程如下[19]：

图3 采矿机器人动力学模型Fig. 3 Dynamic model of mining robot

(4)

其中，M为采矿机器人总质量，FL、FR分别为左、右履带的牵引力，RL、RR为左、右履带所受阻力，fy为侧向阻力，d为重心和顺时旋转中心间的距离，D为采矿机器人两侧履带中心距，L为采矿机器人履带接地长度。

采矿机器人两侧履带的牵引力FL、FR通过与土壤的剪切作用产生，采矿机器人运动过程中，履带所受牵引力可视为履带各点处所受剪切力的合力，牵引力与履带运动的关系可用式(5)表示：

(5)

其中，b为单侧履带宽度；τL[jL(x)]，τR[jR(x)]为土壤剪切应力，jL(x)，jR(x)为距离履带接地段最前端x处的剪切位移。

根据研究[20]，深海海泥的剪切应力—剪切位移特性曲线如图4所示。

图4 土壤剪切力—剪切位移关系Fig. 4 The relation of shear force-shear displacement

从图4中可以看出，随着剪切位移的增加，其剪切应力先快速增大至最大值τmax，随后逐渐减小至残余应力值τres并保持在τres不变。对于该种土壤剪切应力与剪切位移间的关系，Wong等[21]提出了如下关系式：

(6)

式中：Kr为残余剪切应力τres与最大剪切应力τmax的比值。Kω为出现最大剪切应力τmax时的剪切位移，结合矿区土质，Kr取0.28，Kω取0.035[20]。

采矿机器人运动时，采矿机器人履带不可收缩，故履带各点处的剪切位移为：

(7)

(8)

最终获得履带推力与打滑率的关系如图5所示。

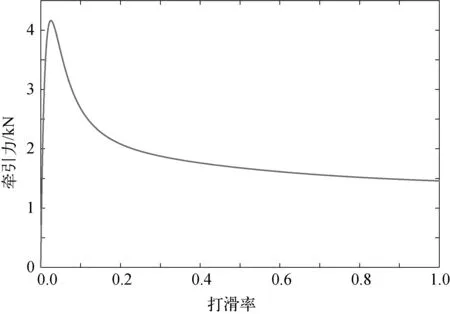
图5 采矿机器人牵引力与打滑率关系Fig. 5 Relationship between traction force and slip rate of the mining robot

由图5可知，打滑率约为2.5%时土壤提供采矿机器人最大牵引力，随着打滑率上升，牵引力逐渐下降并稳定。根据土壤提供牵引力随打滑率的变化关系将其分为3个阶段：正增益阶段，牵引力随打滑率上升增加至最大过程，该过程中，可以通过提高履带转速来增加牵引力；负增益阶段，牵引力随打滑率上升而下降至接近稳定过程，该过程中，由于牵引力随打滑率上升是下降的，此时提高转速，采矿机器人受到的牵引力下降，打滑率将进一步提高导致控制效果反向；无增益阶段，牵引力随打滑率上升基本保持不变，该过程中无法通过改变履带转速来控制采矿机器人。因此将机器人打滑情况限制于正增益阶段内，机器人运动控制效果最好。

采矿机器人运动过程中，采矿机器人径向所受阻力RL、RR主要由两部分组成：压实阻力和推土阻力。

压实阻力[22]可表示为：

(9)

其中，M为采矿机器人质量，b为采矿机器人单侧履带宽度，h为单侧履带承重轮数，p为履带板节距。

推土阻力[20]可表示为：

Rb=b(0.67czKc+0.5z2γKγ)

(10)

其中，γ为沉积物比重，z为土壤压实深度，c为黏聚系数。Kc、Kγ为被动土压系数，可由式(11)、(12)获得：

Kc=(Nc-tan)cos2

(11)

(12)

采矿机器人旋转阻力fy可用式(13)计算[23]：

(13)

式中：μ为履带与地面摩擦系数，取μ=0.08；eG为重心偏心距，假设机器人重心位于形心，即取e=0。

2 路径跟踪算法

采矿机器人跟踪的路径通过一系列带艏向的三维坐标向量表示，如式(14)所示：

(14)

其中，xn，yn，θn分别为路径点的横坐标、纵坐标及艏向坐标。n为当前路径点的编号。

采矿机器人路径跟踪目标艏向角定义如图6所示，图中P1=(xn,yn,θn)为机器人当前目标点，P0=(X,Y,θ)为当前机器人位置。虚线OP1为目标点P1按其艏向坐标θn方向的延长线，O点为采矿机器人位置P0到线OP1的垂足。为采矿机器人设计在当前点的目标艏向，其方程为：

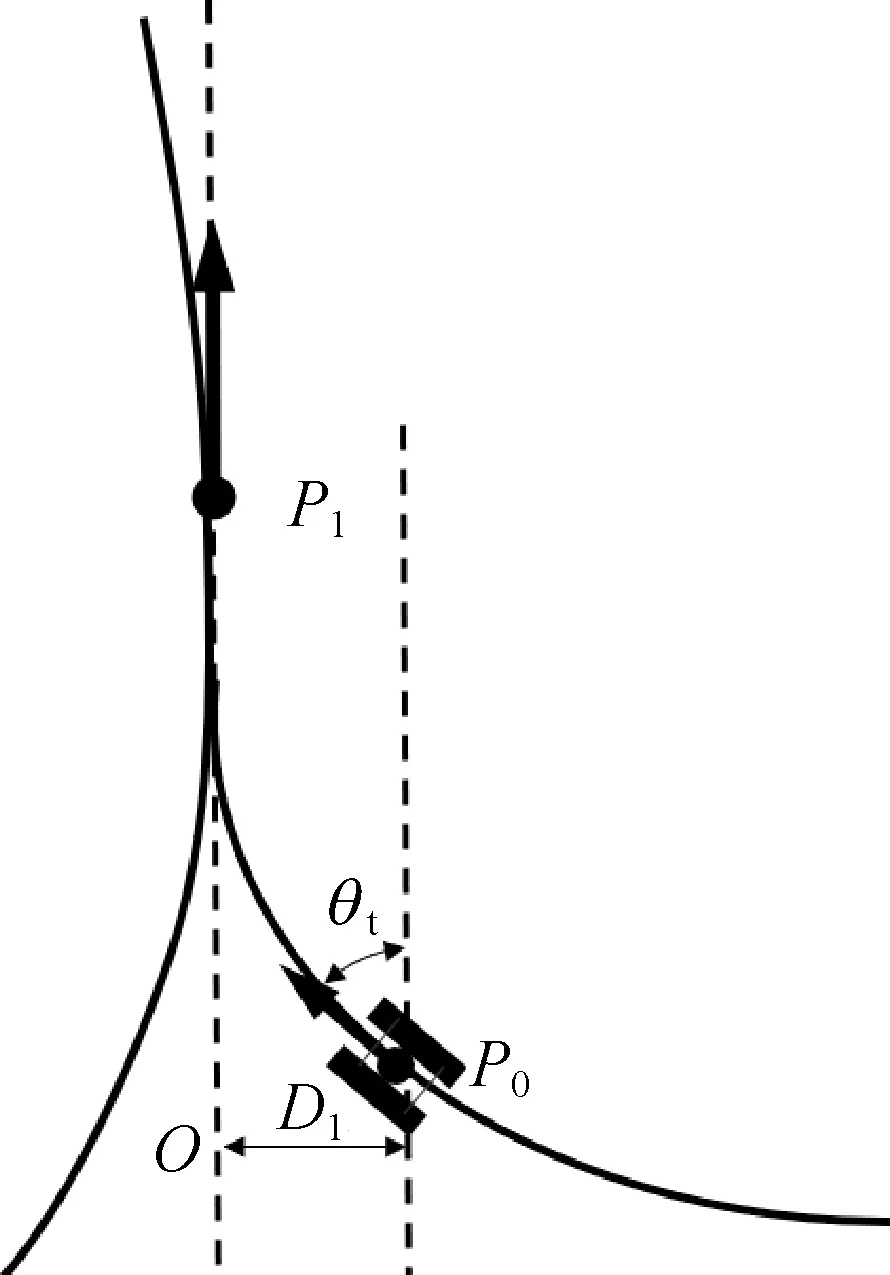
图6 路径跟踪目标艏向角定义Fig. 6 Definition of path tracking target heading angle

θt=arctan(|D1|)×jud(P0,P1)

(15)

式中：D1为P0至虚线OP1的距离。根据P0、P1坐标可由式(16)计算D1：

(16)

其中，dot(a,b)为向量a在b上的投影。Δθ为采矿机器人目标艏向与θn的偏差绝对值，jud(P0,P1)为判断系数用于表示θt的方向，由式(17)获得：

(17)

以设计目标艏向为切线方向，从P0开始作曲线l。沿曲线l运动采矿机器人最终将运动至虚线OP1。D1越大，θt越大，采矿机器人趋近虚线OP1速度越快，系统有更好的快速性；D1越小，θt越小，采矿机器人趋近虚线OP1速度越慢，系统有更好的稳定性。

3 模糊PID控制器

由于采用运动学模型建立控制器未考虑打滑这一重要因素，而采用动力学模型设计艏向控制器存在对模型的精度要求高而打滑模型必然不准确的矛盾，故采用通过运动学模型建立控制器和通过动力学模型分析控制器输入限制相结合的方式设计采矿机器人艏向控制器。

传统的PID控制器由于其结构简单，鲁棒性和适应性强且不依赖于具体模型的特点被广泛用于工业控制中[24]。然而，传统的PID控制器对于强非线性系统，特别是复杂的没有精确模型的系统无法起到良好地控制效果。模糊PID控制器通过增加模糊模块，根据误差及误差变化动态调节PID的控制系数，提高了控制器的精度和响应速度，同时增加了其对没有精确模型的系统控制能力[25]。

采矿机器人艏向角的偏差模型为：

e=θt+θn-θ

(18)

模糊PID控制框图如图7所示，艏向偏差e及其变化率Δe为控制系统输入，模糊控制器根据e及其变化率Δe动态调节PID控制器的控制参数kp、ki、kd，再通过PID控制器计算所需角度差。

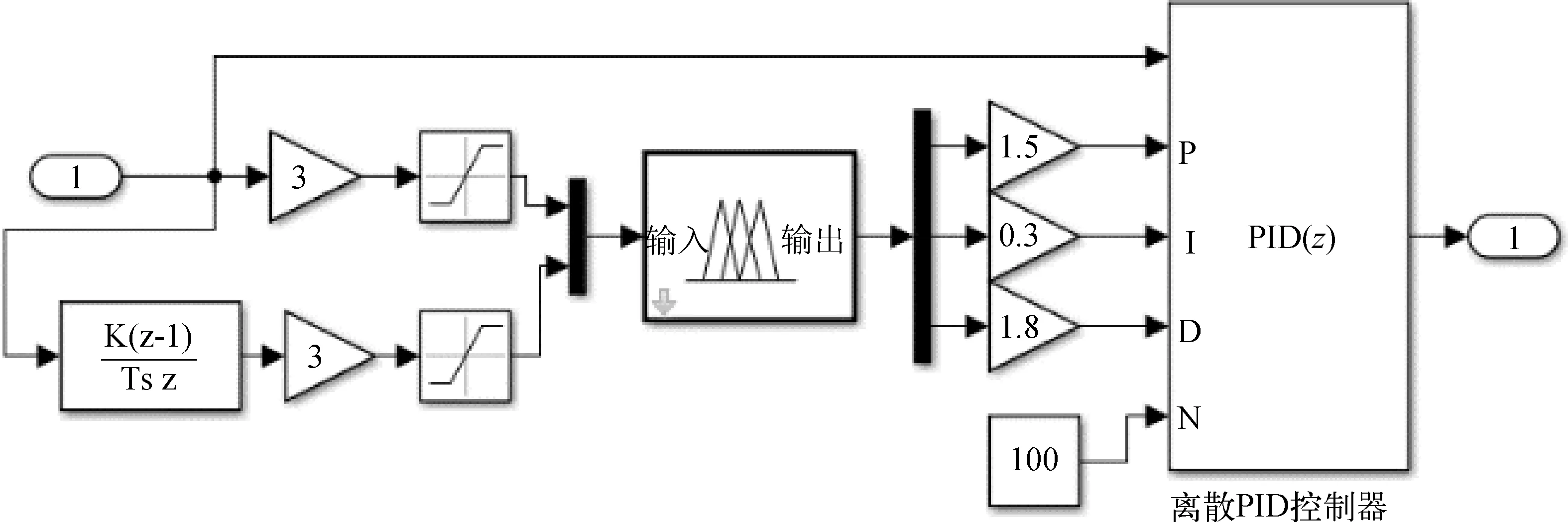
图7 模糊PID控制器Fig. 7 Fuzzy PID controller

E及ΔE为艏向偏差e及其变化率Δe的模糊变量，其论域为{-3,-2,-1,0,1,2,3}。Kp、Ki、Kd为PID控制参数kp、ki、kd的模糊变量，其论域为{0,1,2,3,4,5,6}。

其具体流程如下：系统首先对输入量进行模糊处理，将系统输入e、Δe转换为模糊变量E及ΔE,再通过模糊控制规则表，获得Kp、Ki、Kd，后采用重心法进行解模糊处理得到控制参数kp、ki、kd。模糊控制器的输入输出关系如图8～10所示。

图8 控制参数kpFig. 8 Control parameterkp

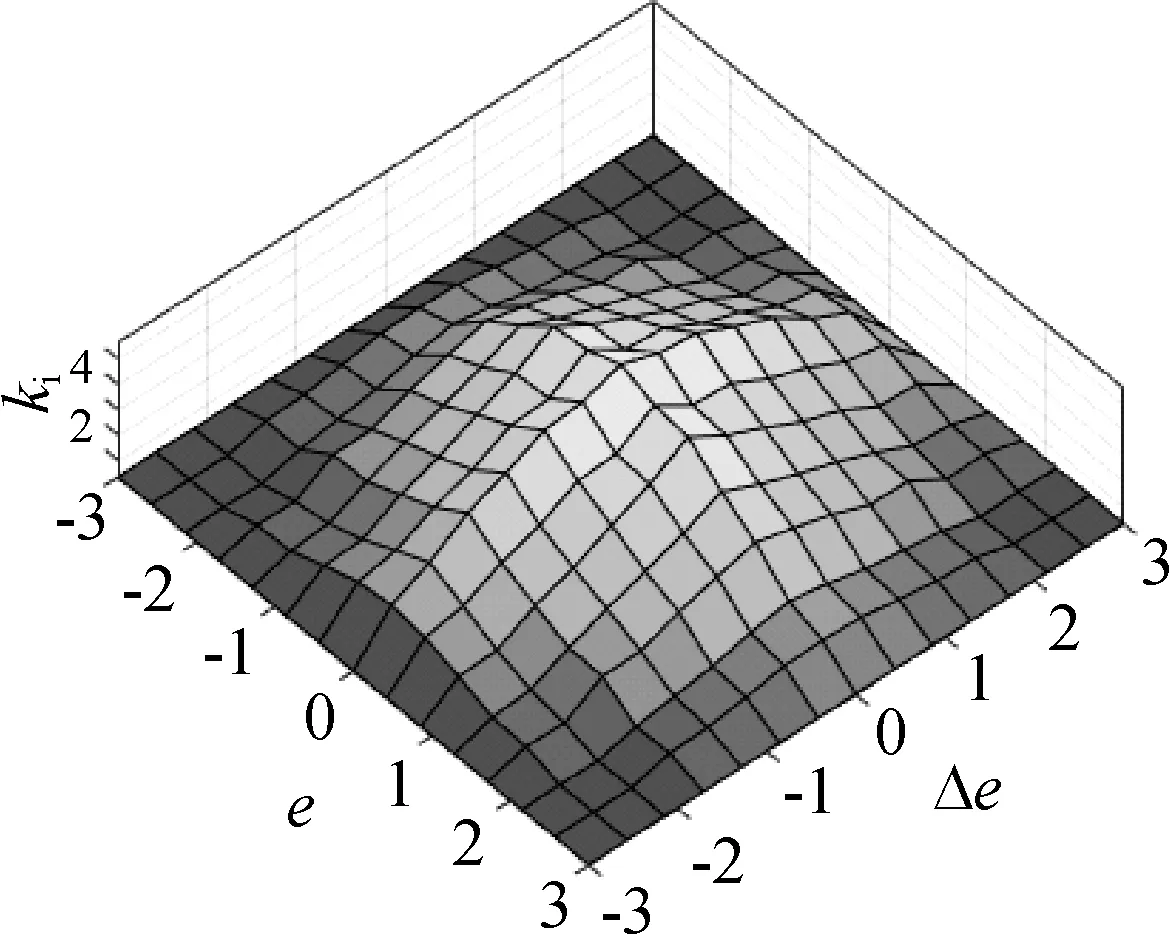
图9 控制参数kiFig. 9 Control parameter ki

图10 控制参数kdFig. 10 Control parameter kd

对于kp，当e为0时，kp取最小值，当e较大时选用较大的kp使系统有较大的调节速度，当Δe增大，kp也适当增大从而保证调节速度。对于ki，当e及Δe较小时，选用较大的ki以增加系统稳定性，当e及Δe较大时，选用较小的ki以减小系统的超调量。对于kd，当e较小且Δe较大时，选用较大的kd以减小系统超调量，当e及Δe为同向且为大值时，选用较大的kd增加系统调节速度，当e及Δe为反向且较大时，选用小的kd减小对比例环节的影响，增加调节速度。

PID控制器获得控制参数后输出两侧主动轮转速差值Δω：

(19)

此时，采矿机器人左右履带主动轮的目标转速为:

(20)

其中，ω0为采矿机器人左右履带主动轮初始转速，ωL、ωR为采矿机器人左右履带主动轮的目标转速。

(21)

式中：ωLs、ωRs为采矿机器人左右履带主动轮实际转速，kω为设定的履带主动轮角加速度。

通过前文对打滑阶段的分析，将打滑率限制于正增益阶段实际控制效果最好，而由于打滑问题非线性且较为复杂，难以直接通过数值求解的方式获得合适的履带主动轮角加速度kω，因此采用数值模拟的方式，模拟不同的履带角加速度下打滑率变化情况及最大打滑，据此选择合适的履带主动轮角加速度值。

首先，为了保证获得的最大打滑率大于等于实际中的最大打滑率，将模拟输入设置为模糊PID控制器输出的最大值，即Δω=4，其后选择不同的履带主动轮角加速度数值仿真获得不同主动轮角加速度下的打滑率，如图11展示了部分kω下打滑率的数值仿真结果。

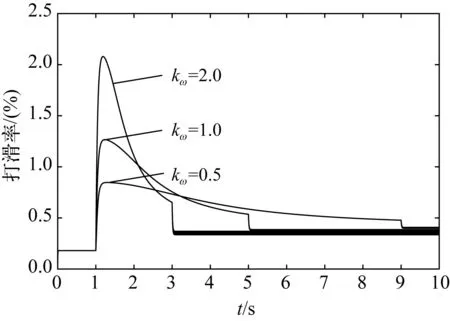
图11 不同kω下打滑率的数值仿真结果Fig. 11 Numerical simulation results of slip rate under different kω

以不同主动轮角加速度为横轴，其对应的加速过程中履带最大打滑率为纵轴作图，如图12所示，从图中可以看出，主动轮角加速度与履带最大打滑率近似为线性关系，为了避免控制输入引起的过度打滑，且使系统有较快反应和一定的打滑余量，最终选择履带主动轮角加速度kω=2 rad/s2。

图12 主动轮角加速度与履带最大打滑率关系Fig. 12 Relationship between angular acceleration of driving wheel and maximum skid rate of track

4 仿真及结果分析

为验证该算法路径跟踪效果，使用Matlab/Simulink软件基于动力学方程建立采矿机器人的动力学仿真模型，并基于该模型对算法进行了数值仿真分析，表1给出了采矿机器人参数及土壤参数。分别针对系统在直线变道、圆周曲线路径和采矿工况下的路径跟踪效果进行验证。

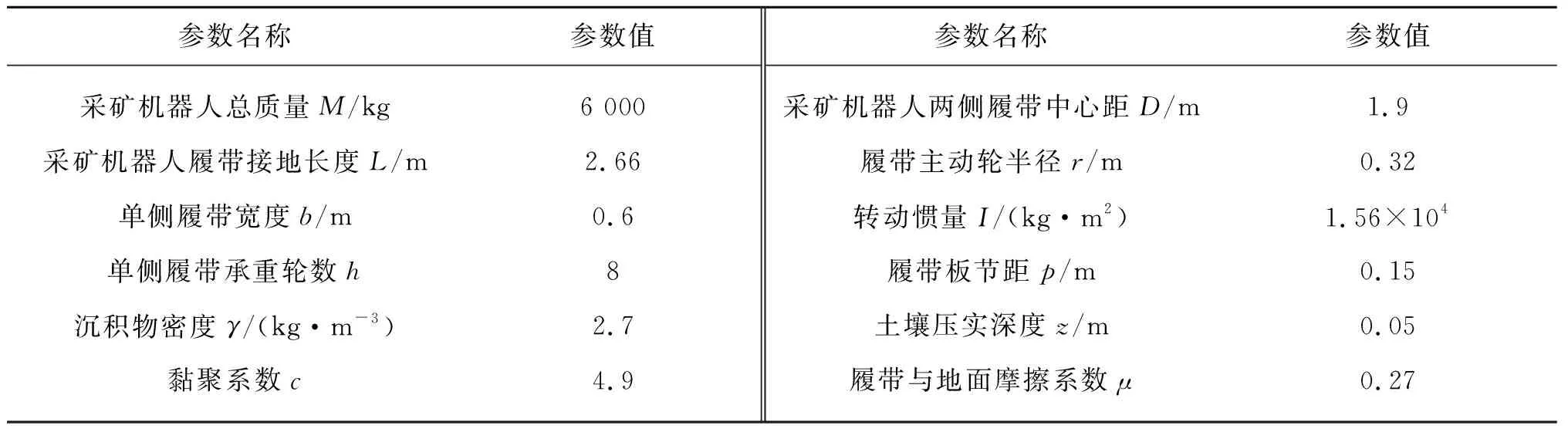
表1 采矿机器人参数及土壤参数Tab. 1 Mining robot parameters and soil parameters

4.1 直线变道

采矿机器人从当前路径变道至相隔一定距离的路径并保持艏向不变。图13为直线变道的仿真结果，两条路径间间隔为8 m。

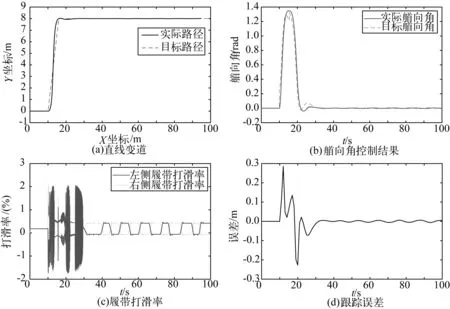
图13 直线变道仿真结果Fig. 13 Simulation results of linear lane change

图13(a)为路径跟踪效果，可以看出，在跟踪变道路径时，采矿机器人跟踪效果优秀。图13(b)为变道工况下采矿机器人的艏向跟踪情况，从图中可以看出，在变道过程中，存在两次目标艏向角的突变，这是由目标点变化造成的，这种突变可以通过改变采矿机器人的提前转向点进行削弱。采矿机器人的目标艏向有一定的滞后但控制器保持良好的控制效果，这同时也解释了采矿机器人运动小幅振荡的原因。图13(c)为采矿机器人两侧履带的打滑情况，在t为13 s时，左侧履带打滑率达到了最大值，在t为10 s时，右侧履带打滑率达到了最大值，两者均在打滑限制范围内，限制打滑效果良好。图13(d)为跟踪误差曲线，从图中可以看出跟踪误差最大值仅有0.3 m且能迅速恢复。

4.2 圆周曲线路径

图14展示了半径为5 m的圆周曲线路径的跟踪效果。从图14(a)中可以看出，跟踪5 m半径的路径时，系统有出色的跟踪效果。图14(b)为采矿机器人艏向跟踪效果，图中目标艏向的每一次跳跃即为一次目标点切换，结合艏向误差，可以看到在初始两个目标点跟踪过程中，艏向误差相对较大，为0.06 rad，随后的目标点误差减小，这说明该控制器具有一定的适应能力。图14(c)为采矿机器人两侧履带打滑率，可以看出打滑率最大值约为0.3%。图14(d)为跟踪误差曲线。

图14 曲线跟踪仿真结果Fig. 14 Simulation results of circular path

4.3 采矿工况

图15展示了采矿工况下的路径跟踪结果，采矿工况的路径由直线及半径为5 m的圆弧组成，并在两侧履带增加了额外的干扰阻力。从图15(a)中可以看出，在直线段，采矿机器人的位置误差仅为4 cm，在全程，采矿机器人均有良好的跟踪效果。图15(b)为采矿机器人艏向跟踪效果。图15(c)为采矿机器人两侧履带打滑率，可以看出打滑率最大值约为0.5%。图15(d)为采矿机器人两侧额外干扰阻力。在前50 s，采矿机器人做直线运动，此阶段采矿机器人运动较稳定，从50 s开始，采矿机器人进入曲线阶段，两侧履带打滑率开始增加。在每次进入及离开曲线段后至稳定前的一段时间内，采矿机器人打滑率均有一定程度的增加，但依旧在2.5%的限度内，说明防止过度打滑效果良好。图15(e)为跟踪误差曲线，对比图15(b)可以看出，在艏向角切换时，机器人的运动偏差较大。

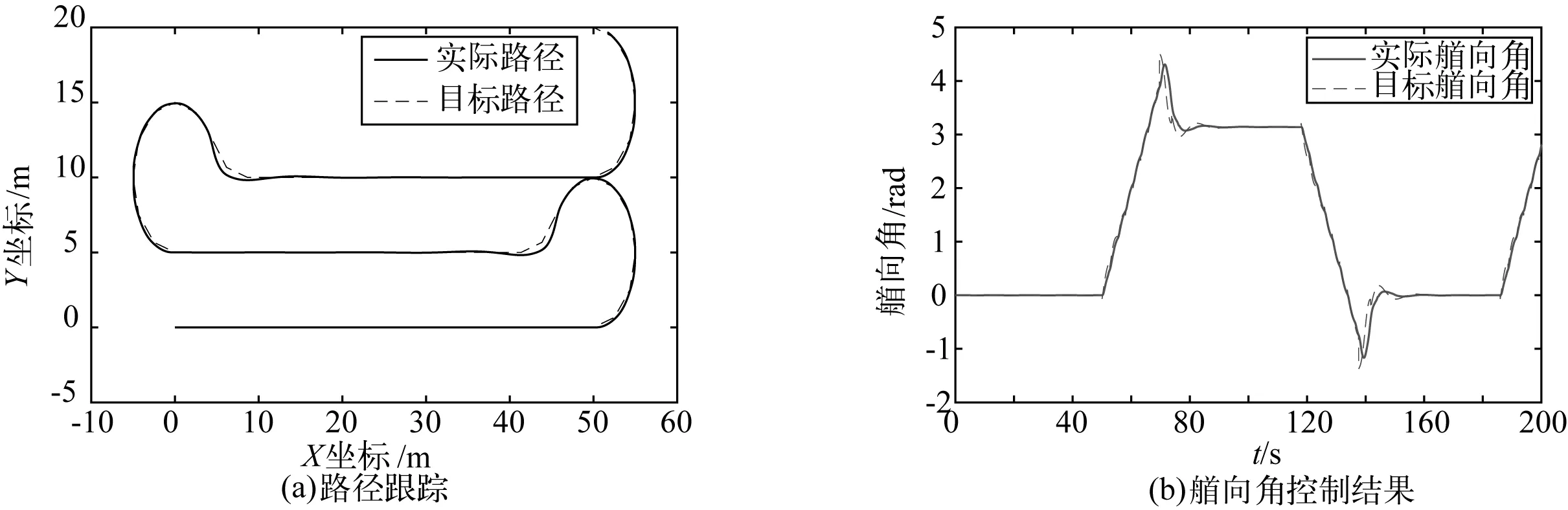
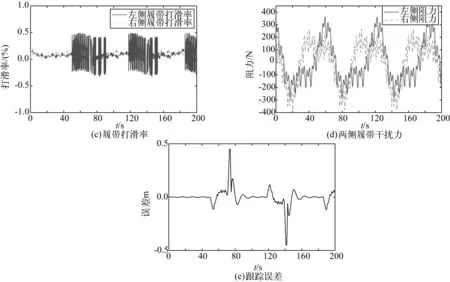
图15 作业工况仿真结果Fig. 15 Simulation results of working path

5 结 语

针对深海采矿机器人路径跟踪问题，经过分析得到如下结论：

1) 提出了一种基于模糊PID的深海采矿机器人路径跟踪控制器。根据采矿机器人与当前目标点相对位置采用反正切函数计算采矿机器人的当前位置目标艏向角，通过采矿机器人按目标艏向角方向运动从而实现路径跟踪。

2) 通过运动学模型建立了采矿机器人艏向模糊PID控制算法，同时为避免采矿机器人过度打滑，通过动力学模型数值模拟获得了最大打滑率和履带主动轮角加速度的关系，并据此限制履带主动轮的角加速度来防止严重打滑。

3) 根据深海采矿机器人动力学模型及海底软泥性质在Matlab/Simulink软件建立了采矿机器人运动仿真模型。对几个典型路径跟踪问题进行了仿真分析，仿真结果表明，基于艏向控制的控制器能够良好地保证采矿机器人按目标路径行走。

虽然该路径跟踪控制器有良好的路径跟踪效果，但其仍存在如下问题需要进一步解决：1)未解决因外界因素导致打滑进入负增益阶段时的控制；2)控制器未达最优状态，可采用深度学习等方法对模糊控制器进行进一步的优化。