含柔性接头的车身薄壁梁骨架结构概念设计方法研究＊

吕超 陈自凯 左文杰

（1.宝山钢铁股份有限公司中央研究院，上海201900；2.汽车用钢开发与应用技术国家重点实验室（宝钢），上海201900；3.吉林大学，长春130025）

主题词：概念设计 骨架模型 柔性接头 断面形状 扭转惯性矩

1 前言

梁骨架结构简单、容易修改，广泛用于概念设计阶段车身结构性能分析与优化设计。日本丰田公司最早用梁骨架模型进行静态弯扭刚度、耐撞性以及NVH 分析，同时开发了相应的CAE软件[1]。沃尔沃公司也开发了梁骨架有限元模型建模和静态分析软件，实现了梁骨架结构的快速建模与分析[2]。Yoshimura 等人[3]对轿车骨架的断面形状进行了系统优化设计，通过提高断面的性能间接提高车身骨架性能。胡平等人[4]建立了车身结构性能快速评价体系，实现了梁单元与铰结构参数化建模。左文杰等人[5-11]对车身梁骨架模型的创建及其优化设计进行了系统研究，全方位地提高了梁骨架结构的性能，但是不能精确求解四室及以上断面形状的扭转惯性矩。

为了提高车身骨架模型的求解精度，许多研究者在梁单元连接位置创建柔性接头。Nikolaidis 等人[12]根据接头的柔度、角位移耦合等力学特性，建立了14参数的接头模型。Suh等人[13]利用超单元法得到接头详细模型的缩减刚度矩阵。Moon 等人[14]提出了刚梁-弹簧简化模型，在梁单元之间创建一组互相垂直的弹簧。黄金陵等人[15]建立了含有接头单元的有限元模型，并讨论了接头柔度对整车刚度的影响。徐涛等人[16]用刚性梁单元和弹簧单元模拟车身接头的变形，此方法可以快速、精确地创建梁骨架模型。此外，Park和Yo[17]利用矩形管梁单元和弹簧单元创建含有柔性接头的客车骨架模型并进行耐撞性分析。以上研究大幅度提高了梁骨架模型性能的求解精度，但这些方法还不能方便地用于车身薄壁梁骨架结构的概念设计。

因此，本文提出了含柔性接头的车身薄壁梁骨架结构概念设计方法，开发相应的建模和分析软件，用于将详细模型缩减为含有柔性接头的梁骨架模型，并对其进行性能分析。

2 薄壁梁断面特性计算

车身梁骨架模型由多种复杂断面梁单元构成，梁单元的刚度需要根据断面的力学特性确定，所以需要精确求解断面形状的力学特性[5-6]。梁单元断面的力学特性主要包括断面面积、弯曲惯性矩、扭转惯性矩和形心坐标。目前，车身断面形状主要包括开口、单室、双室、三室和四室。但是，现有的商业软件只能精确计算三室以内断面形状的力学性能，故本文首先推导任意多室断面形状的力学特性，增强断面形状的可设计性。

2.1 断面面积

图1所示为双室断面形状示意。薄壁梁是由小矩形片段组成的，其断面面积A可表示为：

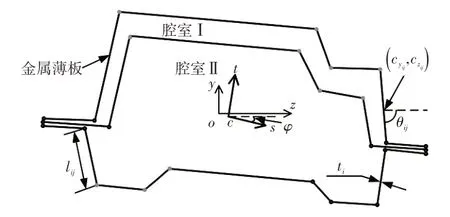
图1 双室断面形状示意

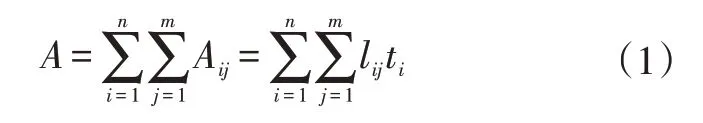
其中，n和m分别为金属薄板及其包含的矩形片段的数量；i和j分别为金属薄板和矩形片段编号；lij和Aij分别为矩形片段长度和面积；ti为薄板的厚度。

2.2 断面形心

通过计算每一个矩形片段的形心的加权平均可以得到断面的形心c的坐标(cy,cz)：

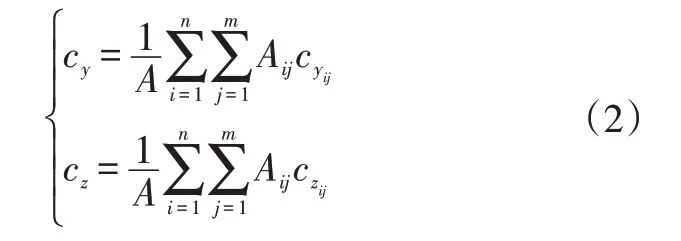
2.3 断面主惯性矩

通过坐标变换的方法（即转轴公式）可以求解断面的主轴s和t的惯性矩，即断面的主惯性矩Is和It：

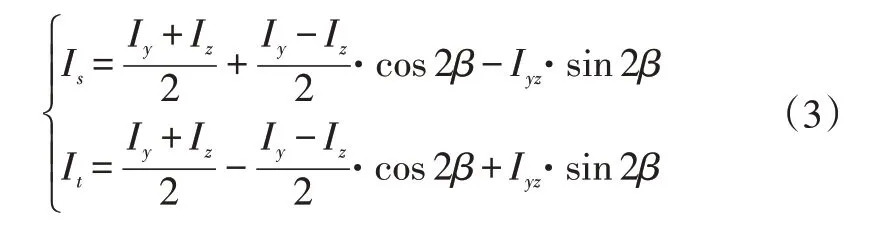
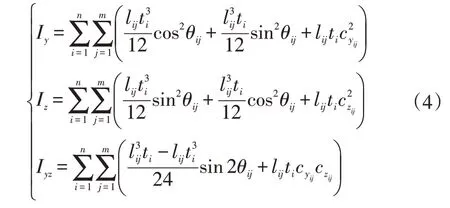
式中，θij为第i个金属薄板中第j个矩形片段与y轴正方向的夹角。

2.4 扭转惯性矩

薄壁断面的扭转惯性矩由断面形状确定，解析推导断面的扭转惯性矩是非常困难的，图2中的5类断面形状的扭转惯性矩解析表达式各不相同，目前商业软件只能精确地计算至三室的扭转惯性矩。

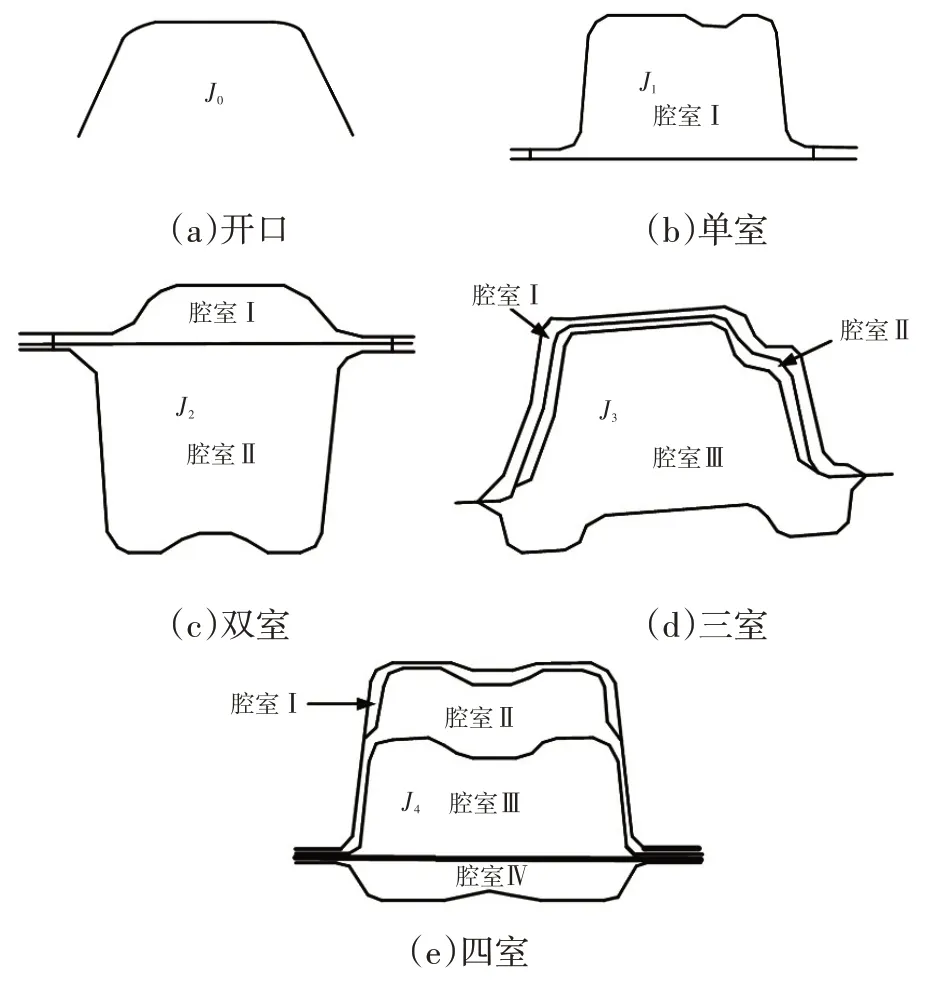
图2 5类断面形状

薄壁断面的扭转惯性矩是通过薄膜比拟推导的[18]，首先，根据薄膜比拟得到薄壁梁的扭矩与断面面积的关系，以及薄壁断面扭转角与剪应力的关系：

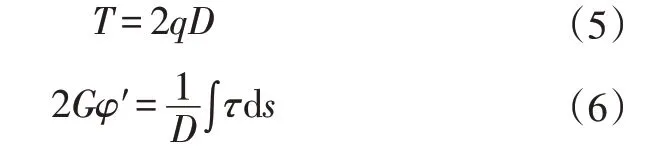
其中，T为薄壁梁的扭矩；D为薄板围成面积；q=τt为薄板的剪力流；τ、t分别为薄壁的剪力和厚度；G为材料的剪切模量；φ为截面扭转角；ds为薄壁的微线段。

结合式（5）、式（6）以及T=GJ1φ'，可得单室薄壁断面的扭转惯性矩J1为：

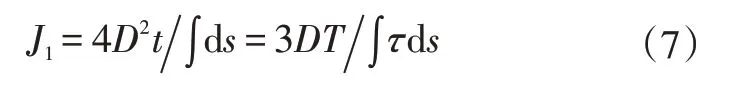
以此类推，利用公式（8）可以计算多腔室断面扭转惯性矩J：

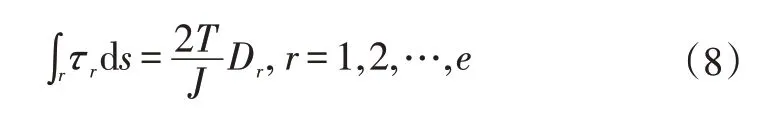
其中，Dr和τr分别为第r腔室薄板围成面积和剪力。

同一腔室的剪应力流相同，共用薄壁的剪应力流计算公式为qrs=qr-qs，其中，qr和qs分别为第r和第s室的剪应力流。

故式（8）可以进一步表示为：

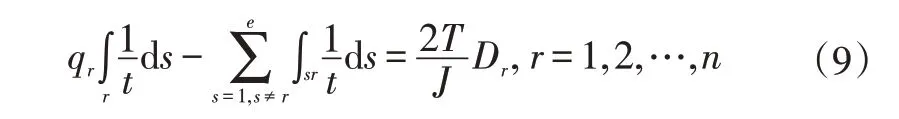
J与T无关，所以假设截面在T=J/2 作用下，求截面相应的剪应力流，再由和，可以进一步计算出任意多室断面形状的扭转惯性矩：

汽车的薄壁断面形状可简化为由线段构成，所以，闭口多室断面扭转惯性矩的计算过程可以简化为：

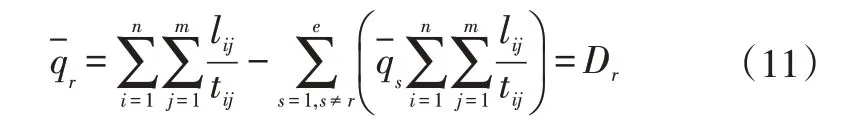
此外，开口部分的扭转惯性矩可以表示为：

任意断面由封闭腔室和开口部分组成，所以任意断面的扭转惯性矩可以表示为：

3 柔性接头建模

本文首先通过求解详细的接头结构获取接头不同方向的刚度[16]，然后将刚度赋值给弹簧单元，最后，通过刚性梁单元和弹簧单元创建柔性接头结构。

3.1 创建接头结构

在HyperMesh中用壳单元创建的接头结构详细模型如图3所示。由于接头端部约束对求解结果有影响，所以接头的各分支需要向外延长一定的长度L=120 mm，在简化车身结构中，试验测量接头的刚度时，接头位置用板固定，所以接头详细有限元模型的端部用刚性梁与形心位置相连接，图4所示为接头端部处理方法，这样处理后的模型，形心的位移与端部节点位移相同。

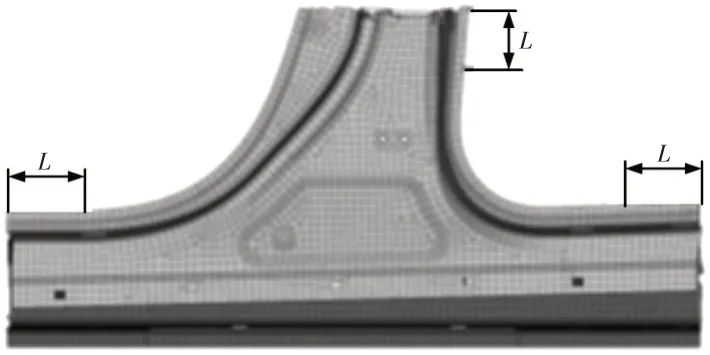
图3 详细接头结构

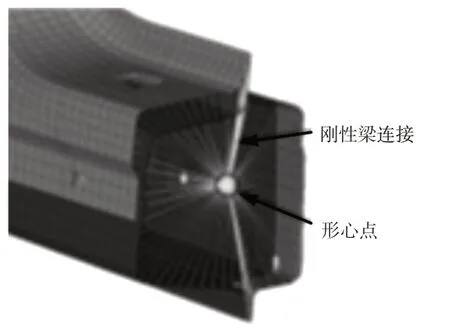
图4 接头端部处理方法

3.2 接头的特性分析

接头某一分支加载，其他分支约束时，加载分支不仅会在X、Y和Z方向产生角位移，还会在各轴向产生线位移，但是与角位移相比，线位移很小，故本文忽略线位移的影响。因此，三分支接头有9种自由度以及相应的9种载荷：

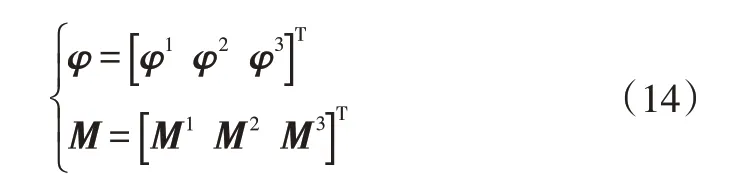
式中，φ和M分别为三分支接头的弯曲角度和载荷列向量；和分别为第i个分支3个方向弯曲角度和弯矩，i=1,2,3。

结构的柔度方程为：

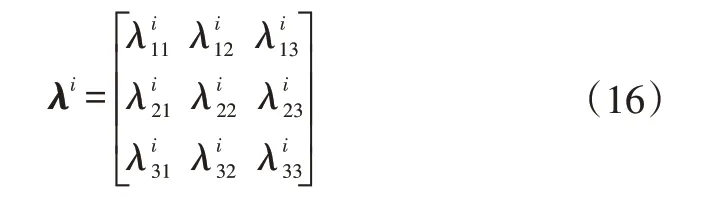
柔度矩阵可借助加载试验获得。一端加载，其他端部约束的柔度方程为：

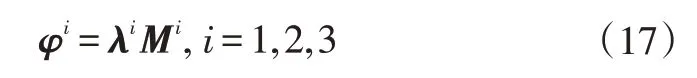
所以三分支结构的刚度矩阵为：

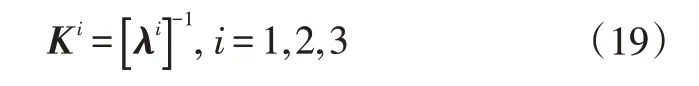
通过加载得到的柔度矩阵是互相耦合的，所以需对式（18）进行矩阵的相似对角化操作，实现解耦，解耦后的方程为：

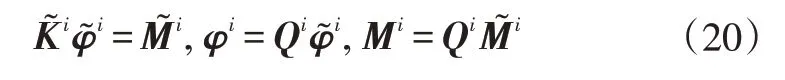
其中，

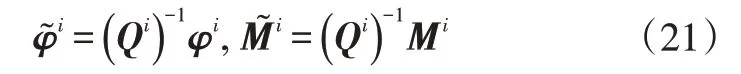
3.3 简化模型的创建

在HyperMesh中创建的刚梁-铰接弹簧接头简化模型由CBEAM单元、CELAS1单元和RB2单元组成。图5所示为创建的接头简化模型，其中1-1'、2-2'和3-3'为3 个刚性梁单元，表示接头的3 个分支，用弹性模量E很大的CBEAM 单元来模拟。3 个分支交于接头的中心点O，节点1'、2'和3'与中心点O连接，且1'、2'和3'节点用只约束角自由度的RBE2 单元模拟，以保证3 个点的线位移相等。取各分支对应的特征坐标系分别作为点1'、2'和3'的节点坐标系，分别为x1y1z1、x2y2z2和x3y3z3。在每2 个分支间有一组零尺寸弹簧单元，用CELAS1 单元来模拟，每组弹簧单元由3 个扭转弹簧构成，3 个弹簧互不相关、相互垂直且方向与节点坐标轴同向。

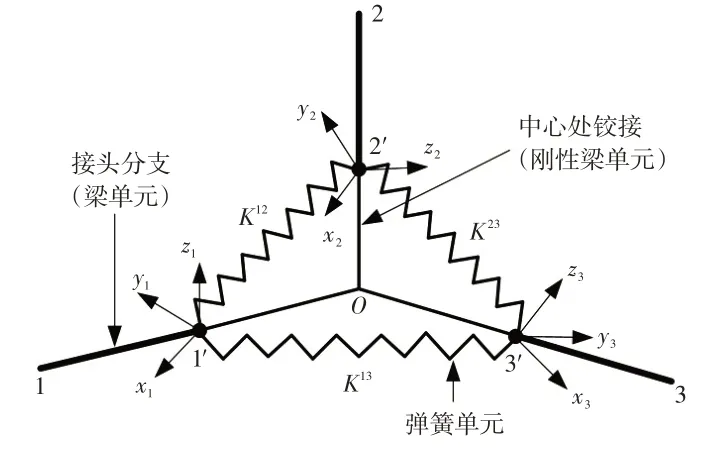
图5 接头简化模型

每组弹簧的刚度写成对角阵的形式分别是K12、K13、K23，通过式（22）求解：

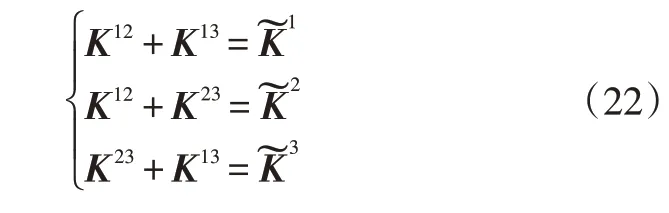
4 车身梁骨架建模软件开发

将白车身有限元模型缩减成车身梁骨架模型的过程可以在HyperMesh中实现。缩减建模过程操作繁琐，需要进行大量重复性工作，因此针对该过程进行了流程自动化开发。车身梁骨架建模软件是对HyperMesh 的二次开发，以Process Studio为开发平台，使用TCL/TK语言，主界面如图6所示。软件的功能是对白车身详细有限元模型进行缩减，得到由复杂断面梁单元构成的车身梁骨架模型。基于详细模型创建梁骨架有限元模型，梁单元创建结果如图7所示；在梁骨架模型中添加柔性接头，柔性接头的创建过程复杂，需要根据详细有限元接头计算得到接头的柔性矩阵，详细有限元接头及其加载工况如图8所示，分析求解结果，输出弯曲刚度、扭转刚度以及模态信息。

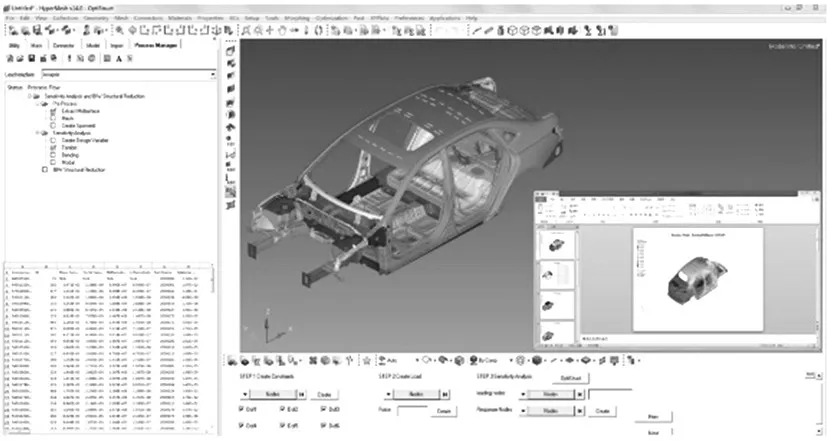
图6 软件主界面

图7 创建好的梁单元及其截面

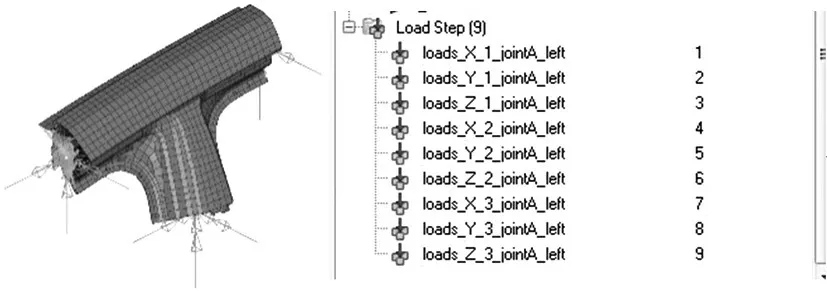
图8 详细有限元柔性接头及其加载工况

5 算例与验证

以某款轿车的白车身为例，使用二次开发的软件对某款轿车白车身骨架结构进行缩减，得到由复杂断面构成的车身薄壁梁骨架模型。图9和图10分别为白车身详细有限元模型和梁骨架模型，2 种模型的质量、质心和转动惯量列于表1中，由表1可知，创建的车身梁骨架模型的3种基本属性的误差都在3%以内。

图9 白车身详细有限元模型

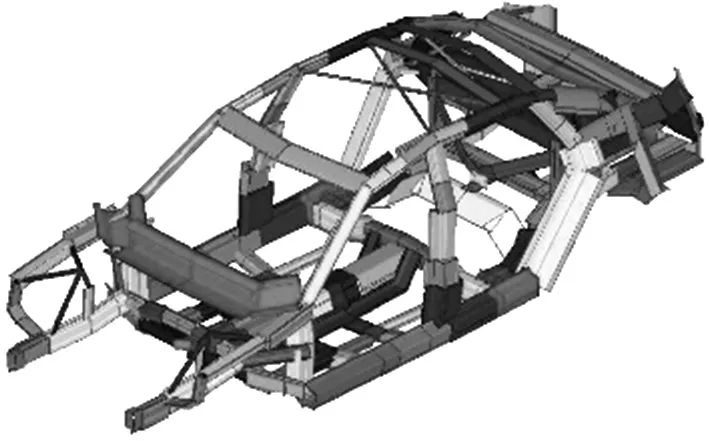
图10 白车身梁骨架模型

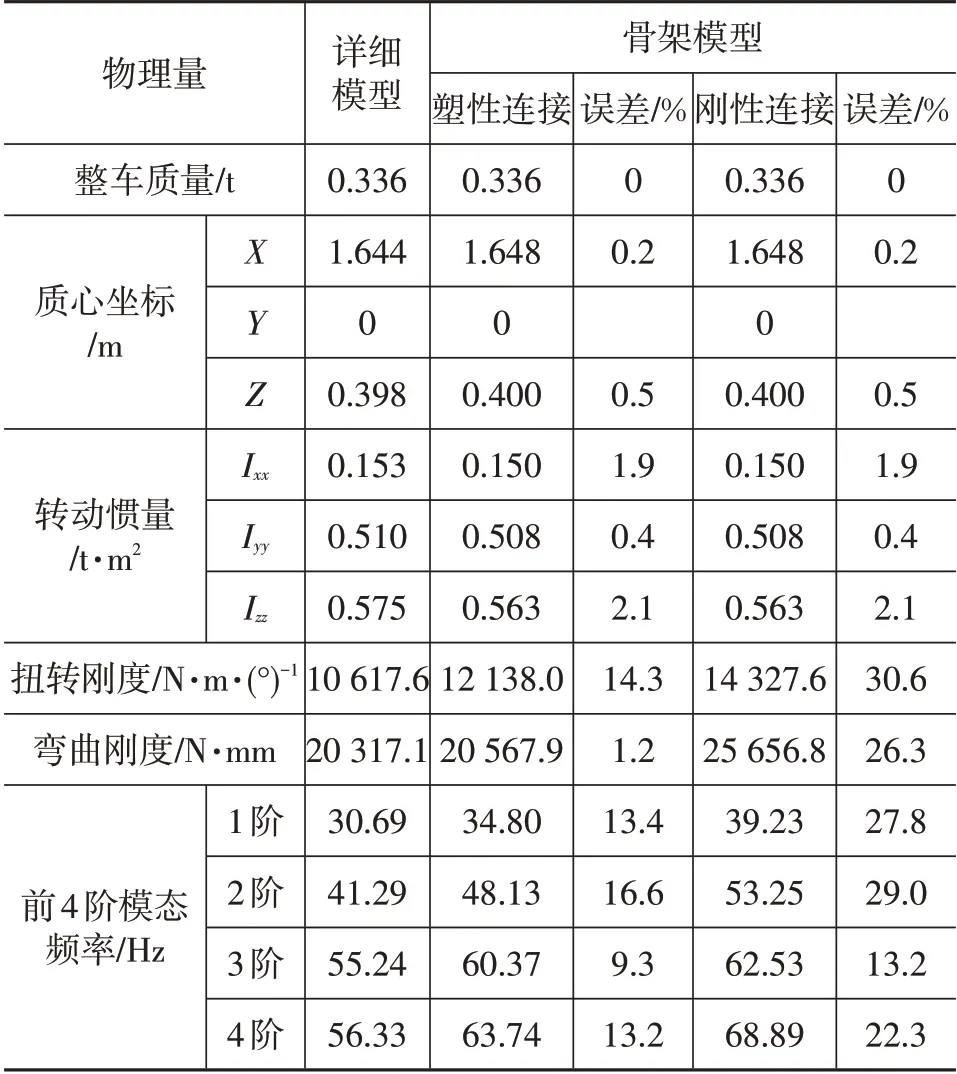
表1 2种模型计算结果对比

对上述2 种模型以及没有考虑塑性铰的梁骨架模型分别进行弯曲工况、扭转工况和自由模态工况的分析，2种模型所得的计算结果见表1。对比2种模型的计算结果可知，所建立的含有塑性铰的车身梁骨架模型的刚度误差在15%以内，而频率误差在17%以内，精度较高。对于没有考虑塑性铰的刚性连接车身梁骨架模型的刚度误差在31%以内，而频率误差在29%以内，相比于含有塑性铰的车身梁骨架模型误差提高了接近1倍。以上数据说明，这种建立车身简化模型的方法是有效的，所建立的车身梁骨架模型能够反映详细模型的特征，可以应用于车身设计与优化。并且，详细模型的求解时间约为15 min，由于自由度相对于详细模型大幅降低，梁骨架模型的求解时间约为40 s，利用梁骨架模型计算时间大幅度缩短。

6 结束语

本文研究了含柔性接头的车身薄壁梁骨架结构概念设计方法。首先，推导了复杂断面力学特性的通用计算公式，弥补了现有商业软件只能计算三室以内断面性能的不足，增强了断面形状的可设计性。然后，基于Process Studio平台，使用TCL/TK语言，开发了相应的建模和分析软件，此软件可以将详细模型缩减至含有柔性接头的梁骨架模型，提高了梁骨架模型的建模效率。最后，对此模型进行性能分析，含有柔性接头的梁骨架模型具有较高的求解精度和效率，满足概念设计阶段低精度、高效率要求。