基于Petri网的并发事件流程模型修复分析 *

杨慧慧，方贤文，邵叱风

(安徽理工大学数学与大数据学院，安徽 淮南 232001)

1 引言

流程挖掘是工作流建模中最有用的工具，它可以从事件日志中获取客观的、有价值的信息，建立流程模型[1]。流程挖掘主要包括3种类型：流程发现、一致性检查和流程增强。但是，通过流程发现得到的模型有时会出现与原始模型没有任何相似之处的情况，这样会丢失原始模型的使用价值，因此为了避免这种损失，许多学者对模型修复的研究越来越关注。

模型修复与流程挖掘的3大类型是不同的。流程发现主要是从工作流日志中发现并提取流程模型，允许用户构建表示记录在日志中的流程行为的流程模型[2]。例如，文献[3]探讨了一类基于业务流程执行事件的在线流的流程发现。还有一些研究侧重于评估所发现的流程模型，文献[4]提出了一种新的方法来评估人为产生的负面事件的流程模型，这种方法允许为发现的流程模型定义行为度量。对于一致性检查，其目的是评估记录在事件日志中的流程模型和事件数据是否一致[5]。文献[6]利用用于交互式流程发现的底层技术提出了一个框架(及其应用)来快速计算一致性，以便增量地更新一致性结果。对于流程增强，文献[7]提供了流程增强的概述，描述了流程增强在各种工业中的应用以及在选择增强方法时考虑增强流程的目标和约束的重要性，相关的增强方法有分解模型修复[8]、使用角色信息来增强业务流程模型[9]等。而模型修复主要针对事件日志与原始模型不符合的部分进行修复，最大程度地与原始模型保持相似。文献[10,11]均研究了修复流程模型的问题，后者提出通过事件日志的触发序列，可以从删除行为、添加行为和更改行为3个方面对流程模型进行修复，修复后的流程模型均可以重放日志，并且与原始模型尽可能相似。因此,模型修复的方法既保留了原始模型的价值，又顺应了现实的流程执行，具有一定的研究价值。

本文余下部分的结构为：第2节介绍与本文相关的基本概念；第3节提出新的修复方法来解决本文所针对的问题；第4节用实例分析本文所提方法的可行性；第5节总结全文并对未来工作做出展望。

2 基本概念

定义1(Petri网)[12]满足下列条件的三元组N=(P,T,F)称作一个Petri网：

(1)P∪T≠∅;

(2)P∩T=∅;

(3)F⊆(P×T)∪(T×P);

(4)dom(F)∪cod(F)=P∪T。

其中,P和T是2个不相交的集合，它们是Petri网N的基本元素集，P中的元素称为P-元或库所，也称为位置，T中的元素称为T-元或变迁，F是Petri网N的流关系。dom(F)={x∈P∪T|∃y∈P∪T:(x,y)∈F}，cod(F)={x∈P∪T|∃y∈P∪T:(y,x)∈F}。dom(F)表示F的定义域，Petri网N的流关系中2个相邻节点x与y之间为因果关系，dom(F)为所有满足条件的x的集合；而cod(F)表示F的值域，是2个相邻节点x与y之间满足cod(F)的条件的所有x的集合。

定义2(迹，事件日志)[13]设Φ是一组活动名称的集合，Φ*是活动发生序列的一个集合，若α∈Φ*是一个活动序列，则称α是一条迹。若L∈B(Φ*)是迹的有限非空的多重集，则称L是一个事件日志。

定义3(对齐)[13]设N=(P,T,F,α,m0,mf)是一个Petri网，其m0为初始标识，mf为终止标识。设α=a1a2…aθ是一条迹，其中θ表示活动序列中触发的活动事件的个数，α到Petri网流程模型N之间的对齐γ=(a1,t1)(a2,t2)…(az,tz)(其中(az,tz)表示对齐中第z组移动对)是满足下列条件的移动序列：

(1)对齐γ的第1行(a1,a2,…,az)是事件日志中的一条迹；

(2)对齐γ的第2行(t1,t2,…,tz)是Petri网流程模型N中的一组变迁发生序列；

(3)对于所有的i=1,2,…,z,如果ti≠≫,α(ti)≠τ,且ai≠≫，那么α(ti)=ai。

这里的移动对满足以下条件：

(1)如果ai=≫∧ti≠≫，则称为模型移动；

(2)如果ai≠≫∧ti=≫，则称为日志移动；

(3)如果ai≠≫∧ti≠≫，则称为同步移动。

定义4(状态集)[14]设Ns=(S,SI,SF,Φ,T)是一个Petri网流程模型N的一个状态集，其中：

(1)S是模型中的状态，SI⊆S是初始状态，SF⊆S是终止状态；

(2)Φ是一组活动集；

(3)T⊆S×Φ×S。

例如，若(s1,act,s2)∈T，则说明状态s1通过变迁act可以转变为状态s2。

3 基于并发事件的模型修复

3.1 最优对齐以及问题的提出

对于给定的迹和Petri网流程模型N，可能会存在多个不同的对齐，为了方便比较不同对齐与流程模型之间偏差的大小，本文分别赋予同步移动、日志移动和模型移动的成本函数值为0,1,1,特别地，(≫,τ)的成本函数值为0。因此，一个迹对齐γ的成本c(γ)为γ中所有移动的成本函数值的和。c(γ)越小则偏差越小，因此本文将考虑最优对齐。

定义5(最优对齐)[15]给定一条迹α和Petri网流程模型N，对于α和N之间所有的对齐χ,∃γ∈χ,对∀γ′∈χ,都有c(γ)≤c(γ′),则称γ是α和N之间的最优对齐。

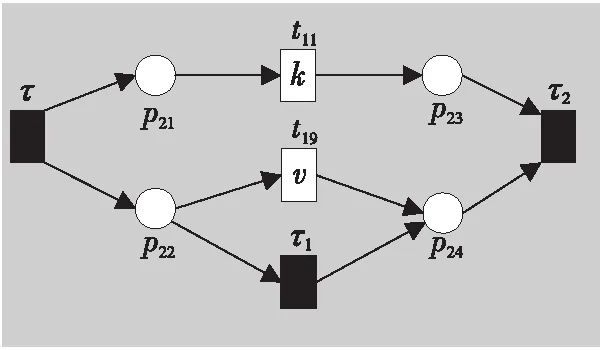
例如，考虑本文第4节给出的迹α1，可以看出α1与事故保险理赔流程模型N之间存在3种不同的对齐，即γ(α 1)、γ′(α 1)和γ″(α 1)，如式(1)所示，由于2=c(γ(α 1))

本文第4节给出了3个事件日志，共有12条迹，其中α1,α6,α7,α11,α12这5条迹与事故保险理赔流程模型存在偏差，但是观察发现这5条迹在现实生活中皆是合理的。交通事故涉及到的纠纷比较复杂，若当事人直接选择走司法程序则会出现α1的情形，由司法程序进行裁决，并对相关损失作出估价；通常需要走司法程序的时候都会开具相关证明，在办理理赔手续的过程需要用到这些证明，即α6和α7；当事故较小时也可以不进行现场勘查，若在允许理赔情况下，当事人对理赔金额存在异议，则保险公司便不执行汇款，等待异议解除后确定了最终金额再进行汇款，即α11和α12。然而这几条合理有效的迹并不能完全在流程模型N中重放，说明理赔系统目前不够完善，应该进一步修复模型,使得模型能更好地反映出各个事件日志。

3.2 重构子流程修复模型

目前，已有的经典修复方法允许简单的插入和跳过活动，在γ(α1)中有2个模型移动，即(≫,h),(≫,j)。活动事件h和j不能在迹中观察到但在模型中却存在，这种情况下允许插入隐变迁跳过相应行为活动来进行模型修复，如图1所示。

Figure 1 Model repair diagram of the insertion of implicit transitions图1 插入隐变迁的模型修复图

图1中变量与本文第4节一致，其中p9～p12表示库所的序号，t7～t10表示变迁的序号，g表示轻微事故，损失较小，h表示重大事故，损失较大，i表示进入司法程序，j表示事故现场勘查检验。对于迹α11和α12与流程模型N之间的最优对齐γ(α11)和γ(α12)如式(2)所示，都包含了2个连续的日志移动(s,≫)和(u,≫)，只是顺序不同，对于这种情况，可以根据文献[13]中基于子流程的修复算法进行模型修复，如图2所示。

γ(α1):=abedcf≫i≫kmlnqrabedcfhijkmlnqrt1t2t5t4t3t6t8t9t10t11t13t12t14t17t18,

γ'(α1):=abedcfi≫≫kmlnqrabedcf≫gjkmlnqrt1t2t5t4t3t6t7t10t11t13t12t14t17t18,

γ″(α1):=abedcfi≫≫≫kmlnqrabedcf≫hijkmlnqrt1t2t5t4t3t6t8t9t10t11t13t12t14t17t18

(1)

γ(α12):=abdcefhijkmlnousprabdcefhijkmlno≫≫prt1t2t4t3t5t6t8t9t10t11t13t12t14t15t16t18,

(2)

Figure 2 Model repair partial display diagram based on subprocess图2 基于子流程的模型修复部分显示图

图2中变量与本文第4节一致，其中p11～p24表示库所的序号，t10～t20表示变迁的序号。根据上述模型修复方法，修复日志移动需要插入相应的活动，那么就有可能发生具有相同行为的同一个活动在模型中不同位置重复出现，分别多次构成自循环的情况，增加了很多不必要的循环行为。例如，式(3)所示的最优对齐γ(α6)和γ(α7)中都含有日志移动(v,≫)，显然,若在模型中插入2次相同的活动v会构成两个自循环结构,如图3所示，模型允许出现活动v多次循环的行为：(…,j,v,v,k,l,m,n,…),(…,j,v,v,v,k,l,m,n,…),(…,j,v,k,v,v,l,m,n,…),(…,j,k,v,v,v,l,m,n,…),…，而日志中并未出现任何循环行为。

Figure 3 Schematic diagram of unnecessary cyclic behavior图3 不必要的循环行为示意图

因此，本文针对类似于γ(α6)和γ(α7)包含的这类对齐提出一种新的修复方法，即先将相关活动的所有流关系断开，然后重新构造一个并发结构的子流程，最后将重构的子流程连接到流程模型中以达到修复效果。

这种修复方法适合修复并发事件,因此本文研究的并发事件符合下列2个条件：

(1)w(w≥2)个对齐中皆含有相同活动事件的日志移动，且原流程模型中不包含此活动事件。

(2)若将此日志移动的活动事件与相邻同步移动的活动事件视为一组并发事件ξ2，且ξ2↑∈βi-1，ξ2∈βi,ξ2↓∈βi+1，其中βi-1,βi,βi+1分别属于块结构工作流网[16]中的一个结构，则有βi-1,βi,βi+1为顺序关系，且在w(w≥2)个对齐中均成立。其中,ξ2↑和ξ2↓分别表示对应迹中ξ2的前一个活动事件和后一个活动事件。

为了筛选符合条件的并发事件，需要考虑流程模型的顺序结构，因此用块结构工作流网[16]来展示更为直观，如图5所示。下面将给出详细的筛选算法。

算法1筛选符合条件的并发事件

输入：所有最优对齐γ，流程模型N。

输出：所有符合条件的并发事件ξ。

步骤2将η1中的对齐进行分组，包含相同日志移动的对齐分为一组，然后将单独成组的对齐删除，设分组完成后形成λ组，即G1,G2,…,Gλ(λ≥1)。

γ(α6):=abdcefhijkvlmnoprabdcefhijk≫lmnoprt1t2t4t3t5t6t8t9t10t11t12t13t14t15t16t18,

γ(α7):=abdecfhijvklmnoprabdecfhij≫klmnoprt1t2t4t5t3t6t8t9t10t11t12t13t14t15t16t18

(3)

步骤3采用流程树语言对流程模型进行描述，列出构成顺序结构的各个分支β1,…,βk*，然后执行步骤4对G1,G2,…,Gλ(λ≥1)分别进行组内筛选。

步骤4观察组内各个对齐，保留日志移动(包含连续日志移动)前后均为同步移动的对齐，其余情况的对齐删除。若|Gi|<2,则删除第i组，否则执行步骤5。

步骤5在Gi中的各个对齐内，设日志移动的活动事件为α，若均满足α↑∈βi,α↓∈βi+1,1≤i≤k-1，则删除Gi，然后对剩余各组执行步骤6。

步骤6在各组中分别对目标日志移动中的活动事件δ进行分析，若将δ与相邻活动事件a视为一组并发事件ξj=[δ，a]，a∈βi并且在组内各个对齐中均满足ξj↑∈βi-1,ξj∈βi,ξj↓∈βi+1,2≤i≤k-1，则保留符合条件的并发事件ξj，否则删除此组对齐。

步骤7得到各组中保留的符合条件的并发事件ξ1,ξ2,…，输出所有符合条件的并发事件ξ={ξ1,ξ2,…}，算法结束。

找到符合条件的并发事件后，便可以对模型进行修复，重构一个并发结构的子流程，然后将其连接到模型中，使得事件日志与流程模型偏差为零，保证了流程模型能够更好地反映出实际事件日志的情况。具体步骤如算法2所示。

算法2重构子流程模型修复

输入:一组并发事件ξj=〈a1,a2,…,a*〉，流程模型N,含有ξj的一组对齐γ(α)。

输出:含有重构子流程的修复模型N′。

步骤4添加一个隐变迁τ,使得τ∈·s′,其中s′={s′i*∈·ti*|i*=1,2,…,n*}；

步骤6将U连接到模型中，满足p′∈·U,pn∈U·，即p′为τ的输入库所，p″为τ′的输出库所;

步骤7得到一个含有重构子流程的修复模型N′，算法结束。

4 实例分析

本节以事故保险理赔流程模型为例，使用本文提出的新方法对原始模型进行修复，使得修复后的模型能够完全重放事件日志，并且尽可能减少不必要的行为发生。最后与目前经典的插入与跳过活动的修复方法进行对比，以验证本文所提方法的可行性。

近年来，随着人们生活水平显著提高，交通事故的保险理赔也越来越受到重视。正常情况下，事故发生之后，第一时间先报案，然后打电话通知保险公司，继而保险公司会进行以下正常的理赔程序：a报案受理;b查询保单信息;c填写出险报案表;d报案登记;e人员调度;f理赔初审;g轻微事故;损失较小;h重大事故;损失较大;i进入司法程序;j事故现场勘查检验;k定损估价;v开具证明;l填写索赔相关材料;m提交相关证明,n理赔复核;o理赔;s暂时不支付;u等待最终确认金额;p汇款;q拒赔;r结案归档。由于事故发生类型错综复杂，事故保险理赔系统难免会出现不符合现实案例的情况，因此进一步完善保险理赔系统是有必要的。本文从保险公司理赔系统中随机调取了部分事件日志，经删除噪声处理后得到如式(3)所示的事件日志：

L1={α1=〈a,b,e,d,c,f,i,k,m,l,n,q,r〉23,α2=〈a,b,d,e,c,f,h,i,j,k,l,m,n,q,r〉316,α3=〈a,b,d,c,e,f,g,j,k,l,m,n,o,p,r〉2952,α4=〈a,b,e,c,d,f,g,j,k,m,l,n,o,p,r〉2710},

L2={α5=〈a,b,c,d,e,f,h,i,j,k,l,m,n,o,p,r〉2108,α6=〈a,b,c,e,d,f,h,i,j,k,v,l,m,n,o,p,r〉18,α7=〈a,b,d,e,c,f,h,i,j,v,k,m,l,n,o,p,r〉31},

L3={α8=〈a,b,e,d,c,f,g,j,k,l,m,n,q,r〉1791,α9=〈a,b,e,d,c,f,h,i,j,k,m,l,n,q,r〉536,α10=〈a,b,c,e,d,f,h,i,j,k,m,l,n,q,r〉824,α11=〈a,b,c,d,e,f,g,k,l,m,n,o,s,u,p,r〉29,α12=〈a,b,d,c,e,f,h,i,j,k,m,l,n,o,u,s,p,r〉16}

(4)

其中，L1，L2，L3表示3个不同的事件日志，αφ(φ=1,2,…,12)表示12条不同的迹，每条迹中后面的数字上标表示这条迹在事件日志中出现的次数。根据这些事件日志，本文构建了基于Petri网的事故保险理赔流程模型N，如图4所示，该流程模型符合一般的理赔程序。根据Petri网定义可知，图4显然满足条件(1)～条件(3)，对于条件(4)，已知对于x∈P∪T，记·x={y|y∈P∪T∧(y,x)∈F}，x·={y|y∈P∪T∧(x,y)∈F}，称·x为x的前集，x·为x的后集，因此，图4中所有变迁与库所中，dom(F)表示相邻2节点x和y满足(x,y)∈F的·y的集合，cod(F) 表示相邻2节点x和y满足(y,x)∈F的y·的集合，即dom(F)={p1,p2,…,p18,p19,t1,t2,…,t17,t18}，cod(F)={p2,p3,…,p19,p20,t1,t2,…,t17,t18}，满足条件(4)，因此，图4是合理的Petri网模型。

通过比对给定的事件日志与流程模型可以发现，事件日志中大多数的迹都可以在流程模型中重放，但α1,α6,α7,α11,α12并不能与流程模型完全拟合，对于α1,α11,α12，前文已经进行了详细分析，本节主要针对α6,α7这类行为，对事件日志L2使用本文提出的新方法对原始模型进行修复。

首先用流程树语言描述流程模型的结构，并用矩形区域将流程树节点表示出来，如图5所示，可以清楚地看到流程模型中的各个结构，即顺序结构、选择结构和并发结构。

→(a,b,∧(c,d,e),f,×(g,→(h,i)),j,k,∧(l,m),n,×(→(o,p),q),r)

Figure 4 Process model N of accident insurance claim based on Petri net图4 基于Petri网的事故保险理赔流程模型N

Figure 5 Block structure diagram of Petri net model N图5 Petri网模型N的块结构示意图

然后根据算法1筛选符合条件的并发事件，具体的筛选过程如表1所示。通过表1可以看出[k,v]是一组符合条件的并发事件，找到并发事件后根据算法2对模型进行修复。首先断开活动k的所有流关系，然后与活动v重构为一个并发结构

Table 1 Main processes and results of filtering concurrent events

最后将U连接到模型中，满足·U={p12},U·={p13,p14},即得到修复后的模型N′，如图7所示。

显然，相较于原始模型，含有重构子流程的修复模型N′可以完全重放事件日志L2。不难发现，在实际生活中，当发生重大事故采取司法程序处理时，都会收到开具的相关证明，以便在理赔手续中提供合法凭证。若使用现有的修复方法，例如，使用目前经典的插入与跳过活动的修复方法所得到的修复模型N1(如图8所示)，可以看出修复模型N1中包含自循环结构，允许无限多的循环行为，因此图8过度概括了日志中出现的行为，导致模型表达不精确。相反，使用本文所提方法修复的模型N′，结构相对比较简单，不包含循环结构，不会多次出现循环活动v的行为，如图7灰色部分所示，只涵盖3种执行顺序：〈k,v〉,〈v,k〉,〈k〉，与L2中的情况完全吻合。

Figure 6 Subprocess U of the refactoring图6 重构的子流程U

Figure 7 Repair model N′ containning the refactored subprocess图7 含有重构子流程的修复模型N′

Figure 8 Repair model N1 with existing methods图8 现有方法的修复模型N1

最后，为了对比N1与N′这2个修复模型的精确性,本文根据文献[14]给出适合度fitness和精度precision的相关公式,如式(5)所示：

(5)

fitness(L2,N1)=1-0=1

fitness(L2,N′)=1-0=1

对于2个模型的精度，根据精度计算公式可得：

显然，0.84<0.97,在适合度都为1的情况下，本文方法修复后的模型精度更高一些。因此，通过上述对比可知，本文提出的方法具有合理性和可行性。

5 结束语

本文在已有研究的基础上,基于事件日志与流程模型之间的最优对齐,提出了一种重构子流程的修复方法。首先根据最优对齐,利用相关算法筛选符合条件的并发事件，并将其重构为一个并发结构的子流程，之后将子流程连接到原模型中完成修复。最后本文通过事故保险理赔系统的一个实例验证了该方法的合理性。

由于本文提出的种方法对于含有复杂结构的流程模型并不能很好地适用，因此，在未来的研究中，我们希望可以进一步拓展，寻找一种在复杂结构的情况下也能普遍适用的修复方法，并尽可能提高相应的适合度以及精度。