一种去除聚类数量和邻域参数设置的自适应聚类算法 *

张柏恺,杨德刚,2,冯 骥,2

(1.重庆师范大学计算机与信息科学学院，重庆 401331； 2.教育大数据智能感知与应用重庆市工程研究中心，重庆 401331)

1 引言

随着大数据与智能化的发展，人工智能领域的聚类技术也被赋予了更为重要的现实意义，在商业选址、金融产品推荐、异常检测等方面也有广泛应用。聚类算法的目标在于无监督地将数据集分割成不同的类或簇，使得同一簇内数据的相似性尽可能大，同时保证簇间数据的差异性也尽可能大。在众多聚类算法中，基于最近邻居的聚类算法在数据挖掘、机器学习、图像处理和模式识别等多个领域有着十分广泛的应用，并且取得了很多不错的成果。

在基于最近邻居的聚类算法中，如何自动推断聚类个数与邻域参数，降低对先验知识的依赖是聚类算法面临的一个挑战。为了获取更为准确的聚类结果，现有聚类算法一般需要预先指定聚类个数。而在针对聚类方法的现实应用中，很难在聚类算法运行之前对聚类个数进行准确的预估。在另一方面，无论是基于k-最近邻居KNN(K-Nearest Neighbor) 原则还是ε-最近邻居ε-NN(ε-Nearest Neighbor)原则，其各自对应的邻域参数k或ε的选取与数据集的分布特点密切相关，算法的性能也会因为参数的不同取值而产生急剧变化。

针对上述参数选择问题，本文提出了基于自然邻居NaN(Nature Neighbor)[2,3]的边界剥离聚类算法NaN-BP(Natural Neighbor based Border Peeling clustering algorithm)。NaN-BP算法结合自然邻居的思想，摆脱了邻域参数的选择问题。通过自然邻居的思想，邻域参数的选择可以不需要大量先验知识的积累。NaN-BP算法通过对数自然稳定状态和对数自然邻居特征值建立具有鲁棒性的自然邻居关系，并在其基础之上以自适应的边界剥离方法完成数据集的聚类分析。因此，NaN-BP算法的整个聚类过程不仅无需人为设置聚类数量和邻域大小，还能够根据数据集自身的分布规律进行边界剥离，进而取得更好的聚类效果。

本文的主要贡献如下：

(1)在自然邻居的概念中，根据数据集的数据分布特点创新性地提出了对数自然稳定状态和对数自然特征值的概念和规范定义，并且给出了特性分析，给自然邻居思想补充了新的理论概念。

(2)针对目标数据集的特性，提出了一种鲁棒的自然搜索算法，通过这种算法能得到符合数据分布规律的对数自然特征值。

(3)结合对数自然稳定状态等概念提出了无需邻域参数的边界剥离聚类算法NaN-BP。该算法消除了邻域参数固定选择的弊端，使得改进后的算法能够对不同形状数据集进行自适应聚类，大幅度提高了算法的自适应性。

(4)NaN-BP算法能够自适应地对不同密度不同分布的数据集进行聚类分析，并且通过实验结果验证了其自适应性和聚类结果的准确性。

2 相关工作

2.1 自然邻居

最近邻居的思想被广泛应用于聚类算法中，几乎所有聚类算法都或多或少地使用了最近邻居思想，且其核心方法均基于KNN和ε-NN[1]。这2种方法都使用了邻域参数，而邻域参数的取值只能凭借经验或者多次尝试才能确定，且严重依赖数据分布情况。针对这一问题，自然邻居方法利用自适应的邻域思想，提出了解决参数问题的新思路。

自然邻居NaN是一种新的邻居概念，这种概念产生于客观现实的认知。自然邻居与KNN和ε-NN最大的不同之处在于自然邻居不需要设置或固定某个参数k或者ε，使得数据集中每个数据的自然邻居数目不尽相同，所以自然邻居是一种无尺度的邻居概念[4]。

将自然邻居的概念融入到聚类算法的思想已经有很多的成果，并且在各个领域中都具备良好的实验效果，例如基于噪声去除的分层聚类算法[5]、基于自然邻域的自适应光谱聚类算法[6]、基于自然邻居的聚类方法[7]和基于自然邻域图的聚类和离群检测算法[8]等。在自然邻居的构建算法中，KNN[9]和逆k近邻RKNN (Reverse K-Nearest Neighbor)[10]2种最近邻居的搜索算法也被广泛应用。

2.2 聚类算法

聚类是将数据点分类为组或簇的任务，并通过簇的概念直观展示簇间数据的差异性和簇内数据的相似性。随着数据分析的关注度逐渐提高，越来越多的聚类算法也被提出。其中基于划分的聚类算法的核心思想是：按照全局优化的标准把数据集划分为若干类。由于基于划分的聚类算法具有很好的理论研究基础且对凸形数据集的聚类效果非常理想，是早期非常经典的聚类思路[11]。但是，由于基于划分的聚类算法自身的全局优化函数的局限性，存在不适用具有流形和凹形数据集等许多问题。基于密度的聚类算法理论上能够适用于任何形状的数据集，但是基于密度的聚类算法对参数比较敏感，不适用于簇之间密度较大或具有复杂流形的数据集[12]。基于层次的聚类算法核心思想是通过某种相似性测度计算节点之间的相似性，并按相似度由高到低排序，逐步重新连接各个节点[13]。层次聚类的优点是距离和规则的相似度容易定义，限制少，不需要预先设定聚类数，但层次聚类复杂度高，奇异值也能产生很大影响。谱聚类算法包含严密的数学逻辑，通过图分割的方法对数据集进行划分，理论上能够解决流形数据问题[14]，然而谱聚类算法很难得到真实的最优解，且算法复杂度较高。

在上述聚类算法中，基于密度的聚类算法的聚类结果更接近日常应用场景，研究人员也针对不同应用领域提出了大量的改进算法，Rodriguez等[15]基于密度聚类算法提出了新颖的CFDP(Clus- tering by Fast search and find of Density Peaks)聚类算法，能够更准确快速地描述密度峰值聚类，且算法复杂度更低。之后在DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[16]的基础上,Ding等[17]基于密度聚类算法对参数敏感的问题进行了改进，提出了一种新的基于密度的OPTICS(Ordering Points To Identify the Clustering Structure)聚类算法，降低了算法对参数的敏感度。Qiu等[18]提出了Grid-based Clustering 算法，主要通过扫描数据集，将数据空间根据所选属性划分为数个网格单元，并将样本点划分到相应的单元中，最后根据单元的密度形成类簇。由于最终的簇是根据网格单元划分的，所以该算法对于密度阈值非常敏感，很容易丢失类簇，当数据集存在密度相差较大的簇时，阈值设置得过高可能会丢失一部分簇，设置得过低则有可能使得本应分开的2个类簇合并。为了进一步提高基于密度聚类算法的效果，Huang等[19]基于聚类中心方法查找中心点提出了QCC(Quasi-Cluster Centers)聚类算法。Campello等[20]在DBSCAN和OPTICS基础上提出了HDBSCAN(Hierarchical Density-Based Spatial Clustering of Applications with Noise)聚类算法，算法只需要一个最小集群参数就能够自动选择密度阈值，但对于噪声点不够敏感。Cheng[21]使用核密度估计函数提出了Mean-Shift聚类算法对数据点进行聚类，迭代地将每个数据点移动到其邻近的稠密区域，然后对移动的数据点进行聚类，但该算法往往依赖于核密度估计器的带宽参数。Shimshoni等[22]提出了自适应Mean-Shift方法，通过根据每个数据点的局部邻域估计每个数据点的不同带宽来克服Mean-Shift核密度估计器依赖的问题，但这种方法通常容易对数据进行过度的聚类划分。Averbuch-Elor等[23]利用边界剥离的思想提出了一种全新的基于中心点的边界剥离聚类算法，并取得了极佳的聚类效果。

边界剥离聚类算法的核心思想是通过KNN和RKNN算法找到每个数据点的最近邻居，然后取逆邻居数排序的前1%的数据作为边界剥离迭代的初始边界点，在初始边界点的基础上迭代剥离数据点，当所识别的边界点的“边界性”方面严格弱于迭代中所识别的边界点时，剥离迭代终止，剩下的便是核心点集。最后使用简化版本的DBSCAN将这些核心点分组到数据簇中，根据每次迭代建立的边界点与非边界点的关联完成自下而上的聚类。

然而边界剥离聚类算法在不同形状数据集上选取的初始边界点极其依赖邻域参数k的选择，从而使得在边界点迭代剥离的过程中从边界点到核心点的过程存在产生偏差的可能，进而影响聚类的结果，甚至在部分数据集中出现极为不合理的数据簇划分。基于上述问题，本文提出了一种新的将自然邻居与边界剥离聚类算法相结合的算法——NaN-BP。该算法既能够保留原来边界剥离聚类的优势，又弥补了边界剥离聚类算法中始终存在邻域参数的缺陷，在不同形状的数据集上都无需设置邻域参数，并自适应得到符合数据分布特征的聚类结果。

3 基于自然邻居思想的边界剥离聚类算法

3.1 自然邻居思想

假设数据集X={x1,x2,x3,…,xn},其中，数据集长度为n，之后涉及的数据集默认为此形式。

定义1(自然邻居) 当数据集处在自然稳定状态时，互为邻居的点即互为自然邻居。即对于任意xi,xj，都有：

xj∈NaN(xi)⟺(xi∈KNNλ(xj))∧

(xj∈KNNλ(xi))

其中，KNNλ(xj)代表数据点xj的λ最近邻域，即xj的前λ个最近邻居组成的集合，λ为自然特征值，其定义如定义3所示。

自然邻居与传统的最近邻居有着很大的区别，在整个自然邻居搜索过程中，不需要邻域参数，根据数据集的分布规律找到每个点的邻居，每个点的自然邻居个数都不一定相同，其邻居的数量取决于数据集的分布，而且能够根据数据集找到每个点的合适的邻居个数。

定义2(自然稳定状态) 依次取k=1,2,3,…,n对数据集X进行KNN查找，在算法查找过程中，当k=r时，数据集中任意一点至少存在另一个数据点与其互为邻居，此时数据集所处的状态为自然稳定状态。

定义3(自然特征值) 当数据集X处于自然稳定状态时，自然邻居特征值λ即为当前的KNN邻域大小r。在整个搜索过程中，自然特征值是实际运行过程的最大循环次数，反映了数据集的分布规律。

3.2 边界剥离聚类基本原理

下面给出边界剥离聚类的相关符号定义和概念。

在边界剥离的迭代过程中，第t次迭代时边界点的集合定义为：

下一次未剥离的边界点集合为:

X(t+1)=X(t)

在识别边界点之后，将每一个边界点与一个离其最近的非边界点相关联，非边界点用关联结点ρi∈X(t+1)来表示。在这一过程中，算法也会将部分点标记为离群点，这些点不属于任何簇。关联节点ρi定义为：

其中,li是一个可变的阈值，若边界点xi到非边界点集合中最近的非边界点xj的距离δ(xi,xj)超过可变阈值li，xi则会标记为离群点，若在可变阈值之内，那么ρi就是距离xi最近的非边界点。

最后经过数次迭代剥离边界点，最终剩余的非边界点就是核心点，每个核心点都有到最初边界点的传递关联，通过文献[22]的方法，逐渐合并每一对可达的核心点，最终通过与核心点的边界点关联和链接来定义候选类簇，同时为了更好地滤除离群点，使用用户定义的最小集群大小值将小集群标记为噪声，返回最后一组的类簇。

3.3 基于自然邻居的边界剥离聚类算法

对于给定数据集X，基于自然邻居的边界剥离聚类方法会先根据数据集的特点，进行鲁棒的自然邻居搜索，找到数据集的对数自然稳定状态，并且当数据集达到对数自然稳定状态时，得到数据集的对数自然特征值。整个自然邻居思想都是非参数的，没有指定集群个数的邻域参数，之后使用对数自然特征值来取代边界剥离的邻域参数k，确定初始的边界点，通过反复剥离边界点，最终剩下的点为核心点，最后核心点根据与边界点之间的传递关联，自底向上完成整个聚类。

整个算法分为2个部分，首先用鲁棒的自然邻居搜索算法对数据集进行对数自然邻居搜索，使数据集达到对数自然稳定状态，得到数据集的对数自然特征值；其次根据数据的分布规律得出对数自然特征值，生成合理的初始边界点，然后进行边界点迭代剥离并逐步完成聚类。

定义4(噪声点集-NOS) 对数据集进行自然邻居搜索，当搜索迭代次数达到λ时，噪声点集中任意数据点没有对数自然邻居,其形式化定义为:

xi∈NOS⟺KNNλ(xi)=∅

定义5(对数自然稳定状态) 给定数据集X={x1,x2,x3,…,xn}，在自然稳定状态的查找过程中，数据集除了噪声点外，其他数据点在搜索查找深度达到λ+lnn时，都存在至少一个自然邻居，称之为对数自然稳定状态，其形式化定义如下：

∀xi,xj∈NOS⟹(xj∉KNNλ(xi))∧

(xj∉KNNλ+ln n(xi))

当数据集中存在噪声点时，会大大增加自然邻居的搜索难度，所以将数据集的长度的自然对数与自然特征值λ的和(λ+lnn)作为搜索次数的阈值。使用鲁棒的自然邻居搜索算法，当自然邻居的个数不变次数超过阈值，便认为已达到对数自然稳定状态。

定义6(对数自然特征值) 当数据集X处于对数自然稳定状态时，针对对数自然稳定状态，本文提出了对数自然特征值，其形式化定义如下：

r=(λ+lnn)λ∈N,ln n∈N{λ|∀(xi,xj∉NOS)∧

∃(xj∈KNNλ+ln n(xi))∧(xi≠xj)→

∃(xi∈KNNλ+ln n(xj))}

其中,λ+lnn表示鲁棒的自然邻居搜索算法查找的深度，对数自然特征值根据数据集的分布特点，同时也可以作为传统KNN邻域参数的参考。

定义7(对数自然邻居) 当数据集处在对数自然稳定状态时，互为邻居的点即互为对数自然邻居。即对于任意xi,xj都有：

xj∈NaN(xi)⟺

(xj∈KNNλ(xi))∧(xi∈KNNλ(xj))

本文所提出的鲁棒的自然邻居搜索算法如算法1所示：

算法1自然邻居搜索算法

Input:X={x1,x2,x3,…,xn}∈Rd。

Output:自然特征值λ,逆邻居数Rnum(i)。

/*初始化逆邻居数Rnum(i)，r-最近邻域KNNr(xi)和逆r-最近邻域RKNNr(xi)*/

Initialization:

r=1,Rnum(i)=0,KNNr(xi)=∅,RKNNr(xi)=∅;

//计算数据集的长度，并取自然对数得到终止阈值

ξ=ln(n);

//创建一棵KD-树

KD-tree=creatKDTree(X);

While(Flag= 0)

//利用KD-树搜索数据xi的第r个邻居yr

Rnum(yr)=Rnum(yr)+1;

KNNr(xi)=KNNr(xi)∪{yr};

RKNNr(x)=RKNNr(xi)∪{xi};

计算Rnum(i)=0的元素个数Rzero;

IFRzero不变

T=T+1;

EndIF

IF(T<ξ)

r=r+1;

Else

Flag= 1;

EndIF

EndWhile

λ=r;

算法1中KNNr(xi)表示由数据xi最近的r个最近邻居组成的r-最近邻域。RKNNr(xi)表示由数据xi最近的r个逆最近邻居组成的逆r-最近邻域。鲁棒的自然邻居搜索算法首先给每个数据点找1个邻居，然后计算数据集中逆邻居点为0的点数，再给每个数据点找2个邻居，计算数据集中逆邻居点为0的数据点的数量Rzero。邻居搜索过程中，算法不断增加每个数据点邻居的个数，并且更新逆邻居点为0的数据点数量Rzero。若逆邻居数为0的点数在ξ次没有发生变化，算法便判定当前搜索达到对数自然稳定状态，此时所寻找的邻居数即为对数自然特征值λ。

图1展示了NaN-BP算法中初始边界点选取的优越性。通过对比可以看到，NaN-BP算法中用深色点标识的初始的边界点更符合边界点的定义。特别是在图中标注的圆圈内，从直观上可以看出，其处于簇心位置，明显应该是核心点的候选，而不应该被当前步骤标记为边缘点。NaN-BP算法确定的边界点在这几处基本为零，而BP算法将部分核心点判定为不合理的边界点。图1形象地证明了在不同形状的数据集上，使用NaN-BP算法产生的初始边界点要比BP聚类算法产生的初始边界点更加合理，初始的边界点除去远离类簇的噪声点，基本上都合理地分布在类簇边缘。而BP聚类算法在不同形状的数据集上初始边界点的确定不够理想，导致了对数据集的自适应能力不足，进而严重影响后续算法中核心点的选取。

Figure 1 Comparison of initial border points in two algorithms图1 2个算法的初始边界点对比

定义8(相似性度量) NaN-BP算法采用欧几里得距离和高斯核σj构建函数相似性度量f来反映数据点之间的距离，其定义如下：

基于对数自然特征值的边界点迭代剥离聚类算法NaN-BP如算法2所示：

算法2基于自然邻居的边界剥离聚类算法NaN-BP

Input:X={x1,x2,x3,…,xn}∈Rd。

Output:Cluster indicesC。

r←Algorithm 1;

//通过对数自然特征值生成初始边界剥离点

X1←X;

Forpeeling iteration 1 ≤t≤Tdo

Foreach pointxi∈Xtdo

EndFor

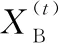
X(t+1)←X(t);

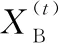
ρi←ASSOCIATEPOINT(xi,X(t+1))

EndFor

EndFor

//根据核心点的关联完成聚类，ρ的ρi组成的集合

整个算法的核心步骤由以下2部分组成：(1)自适应数据集达到对数自然稳定状态，生成对数自然特征值；(2)利用对数自然特征值确定合理的初始边界点，进行边界剥离聚类。算法1和算法2的伪代码对其步骤进行了详细的描述。NaN-BP算法首先解决了原有BP聚类算法固有邻域参数的缺陷。算法利用鲁棒的自然搜索算法使数据集达到对数自然稳定状态，同时得到对数自然特征值和对数自然邻居，能根据不同形状的数据集产生不同的对数自然特征值。在此基础上，算法用对数自然特征值取代原有BP聚类算法邻域参数，因此能够在不同数据集上得到更好地聚类效果。其次，NaN-BP算法得到的邻域参数能更好地适应数据集分布规律，在边界点迭代剥离的过程中能够建立良好的初始边界点。在边界点剥离的过程中，初始边界点的确立对于不同形状数据集的最终聚类效果有很大的影响。BP聚类算法采用固有的邻域参数，当面对不同形状数据集时，初始边界点确立的自适应能力明显不够。而NaN-BP算法很好地解决了这个问题，并在后续实验中形象地展示了其优越性。

4 实验

为了评估基于自然邻居的边界剥离聚类算法更加具有普适性，本文选取了6个不同形状的数据集(flame、R15[22]、Compound、D31、data_DBScan和artificialdata[4])进行了测试，并将其与边界剥离聚类算法进行了性能对比。边界剥离聚类算法的最终聚类效果很大程度上依赖于初始边界点的确定，初始边界点的确定与邻域参数k有着直接关系，所以本文在不同形状的数据集上对边界剥离聚类算法依旧保留原有的固定参数。算法根据数据特征自适应得到的可变邻域能对边界剥离的初始边界点进行更为准确的判断，因此在无需预设参数的情况下，算法在不同形状的数据集上都有很好的效果。

实验部分按照数据集的特性，分别从有监督、无监督和高维大数据3个角度展开了对比，在多种评价维度上验证了本文提出的NaN-BP算法的优越性。

4.1 有监督数据集实验

为了验证本文NaN-BP算法的优越性，选取了BP聚类算法中使用过的人工数据集进行对比实验。实验选取的4个数据集均带有真实标签，评价指标为ARI和AMI。

ARI是描述随机分配类簇标记向量的相似度指标，定义为:

其中，E表示期望，max表示取最大值，RI是兰德系数。

AMI是基于预测簇向量与真实簇向量的互信息分数来衡量其相似度的，AMI越大相似度越高，定义为:

其中,E{MI(U,V)}为互信息MI(U,V)的期望，H(U)和H(V)为信息熵。

在数据集(flame、R15、Compound和D31)上的实验结果如图2所示，在数据集flame和R15上，本文NaN-BP算法有不弱于原有BP聚类算法的竞争力，在R15数据集上甚至效果更好。在另外2个不同形状的数据集Compound和D31上，本文算法的优势非常明显。Compound数据集上的实验结果显示本文算法能够较好地区分不同形状数据集的类簇，而D31数据集上的结果表明本文算法对离群点的确定也更合理。

Figure 2 Experimental results comparison with BP clustering algorithm on flame,R15,Compound and D31 data sets图2 与BP聚类算法在flame、R15、Compound和D31数据集上的实验结果比较

表1详细列举了图2中前2个数据集(flame和R15)上的评价结果。图中Det# 表示最终聚类的个数，K在BP算法中表示人为设置的邻域参数，在NaN-BP算法中由于无需设置参数，因此其表示自适应计算生成的自然邻居特征值。可以直观地看到，本文提出的NaN-BP聚类算法在原文使用的2个不同形状的数据集上依然能表现出良好的效果，特别是在表中邻域参数部分，BP算法是人为预设的参数，所以无法针对数据集的特征进行调整，而NaN-BP算法无需设置这一参数，同时在ARI和AMI评价指标上表现出更为优秀的结果。

Table 1 Performance comparison on flame,R15 data sets

表2详细列举了图2中后2个数据集(Compound，D31)上的评价结果。通过其可以直观地看到，在另外2个不同形状的有监督数据集Compound和D31上，NaN-BP算法生成的对数自然特征值都很好地自适应了数据分布规律，并且在ARI和AMI2个评价指标上都超过了BP聚类算法，表明本文算法对不同形状数据集具有很好的自适应力。

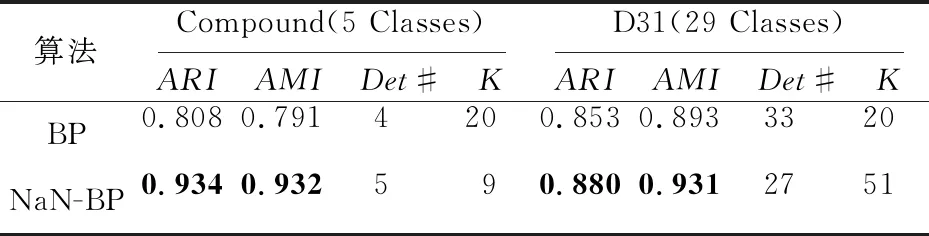
Table 2 Performance comparison on Compound,D31 data sets表2 数据集Compound,D31上的性能比较

4.2 无监督数据集实验

为了证明本文NaN-BP算法在无监督数据集上依然具有很强的竞争力，接下来使用2个不同形状的数据集(data_DBScan和artificialdata[4])分别对BP聚类算法和NaN-BP算法进行了测试。在这种具有大量离群点的球型数据集上，NaN-BP算法取得了更为直观和显著的聚类效果提升。除了聚类结果之外，本文所提出的NaN-BP算法能够根据不同的数据分布特征自适应地进行邻域分析，从而使得边界剥离的初始边界点在数量和位置上都要比BP聚类算法更加优越。

在数据集data_DBScan和artificialdata上的实验结果如图3所示。本文所提出的NaN-BP算法表现出很强的自适应性能，正确地恢复了原有的簇数量，并且在离群点的确定上也有很好的效果。作为对比，BP聚类算法没有得到有效的聚类结果，并且最终离群点的划分也很不理想。这也说明了NaN-BP算法在不同形状、不同聚类数量的数据集上具有自适应能力，而这种自适应产生邻域参数的方法，在边界剥离的过程中，能够更好地确定初始边界点，同时也在很大程度上优化了最后的聚类结果和离群点的划分。

Figure 3 Experimental results comparison with BP clustering algorithm on data_DBScan and artificialdata data sets图3 与BP聚类算法在数据集data_DBScan和artificialdata上的实验结果比较

实验表明，在具有大量离群点的无监督数据集上，在聚类数量和聚类质量等多个方面，NaN-BP算法的聚类效果都要远优于BP聚类算法的。

Figure 4 Comparison of embedding results between BP clustering algorithm and NaN-BP algorithm on three data sets图4 BP聚类算法和NaN-BP算法在3个数据集上的聚类结果比较

4.3 大数据集上的实验

接下来本文将通过规模更大的数据集进一步验证NaN-BP算法的优越性。本文选用MNIST作为大规模高维数据的测试对象，并通过卷积神经网络CNN(Convolutional Neural Network)生成具有500维特征的有标签的高维多分类数据[24]。为了进一步验证NaN-BP算法的自适应性，在原始数据集的基础上随机生成簇数未知并且形状不定的数据集，并通过在大数据集上不同半径内数据随机采样的方法，最终得到3个数据集(D1、D2和D3)。这3个数据集的采样半径分别为120，130，140，每个数据集包括上千条数据，数据维度为500。再对采样的数据进行降维处理，将原始数据的维度从500降至30。通过分析图4可以看出，针对3个不同形状数据集的特点，本文NaN-BP算法依然能自适应生成对数自然特征值，使得边界剥离的初始边界点选取更具有普适性，而且在离群点的确定上本文算法更加合理。尤其在D2和D3数据集上本文算法的聚类效果表现出比原有BP聚类算法更好的竞争力。

表3所示为BP算法和NaN-BP算法在数据集上进行10次聚类分析得到的结果平均值。从表3的实验结果可以看出，NaN-BP算法产生的结果在高维数据集上有着很好的表现，虽然在数据集D1上NaN-BP算法略差于BP聚类算法，但最后的聚类评价指标差距不大。在数据集D2和D3上本文算法各个性能都超过了BP聚类算法，最终表现的聚类效果也更好。

4.4 算法性能和运行细节

Table 3 Performance comparison with BP clustering algorithm on MNIST data set 表3 在MNIST数据集上与BP聚类算法的性能比较

2.30 GHz Intel Core i5的Windows 10系统上实现的，在运行时间上，因为使用自然邻居的改进，整体的运算时间要比BP聚类算法稍长，但相对最后比较理想的效果来说，运行时间的增加完全可以忽略。

4.5 实验小结

为了证明NaN-BP算法对数据集的自适应聚类结果，本文在各种不同形状、不同维度的数据集上都做了对比实验。多组实验结果表明，NaN-BP算法能够自适应地解决不同数据集的邻域参数设定问题，得到了效果良好的初始边界点，并取得了令人满意的聚类效果。同时，NaN-BP算法与BP聚类算法的对比结果也表明了本文算法在面对不同形状的数据集聚类时，具有更好的自适应性和稳定性。

5 结束语

本文针对聚类算法中聚类数目和邻域参数等参数自适应问题，提出了一种基于自然邻居思想的边界剥离聚类算法——NaN-BP算法。NaN-BP算法通过鲁棒的自然搜索算法，自适应不同形状的数据集，生成反映数据集分布规律的对数自然特征值，利用对数自然特征值取代固定的邻域参数。当数据集达到对数自然稳定状态时，同时得到数据集的对数自然特征值和对数自然邻居，对数自然特征值也体现了数据的分布规律。当达到对数自然稳定状态时，每个数据点的对数自然邻居数不一定相同，不同的邻居数更进一步体现了数据集的数据分布规律。NaN-BP算法使用自然特征值能够根据不同形状的数据集确定更理想的初始边界点，使得在边界剥离的逐次迭代中边界点与核心点的关联更加合理，最后自下而上的聚类便能产生很好的效果。

与其他聚类算法不同的是，本文算法使用自然邻居思想，能够根据不同形状的数据集自适应产生理想的初始边界点，实验也表明初始边界点分布对最终的聚类效果有很重要的影响。在整个实验中，不论在BP聚类算法原有的实验数据集上，还是在其他大量不同形状的数据集上，本文算法都比原有的BP聚类算法更具竞争力，自适应能力也更加理想。

虽然NaN-BP算法在参数自适应和聚类结果上都取得了令人满意的成果，但其仍然有进一步提升的空间。在后续的工作中，将在保持算法无需邻域参数的核心优势的同时，尝试通过算法的优化进一步提高NaN-BP算法在半监督数据集上的聚类结果，并进一步加强针对现实场景中聚类分析的普适性研究。同时，在自适应邻居关系的构建方面，将探索流形数据交叠与自动数据标记等问题，尝试对自然邻居思想进行有针对性的改进与优化，探索自然邻域图和动态邻居等思想对聚类算法的改进与提高。