基于双曲正弦函数的四翼忆阻混沌系统及其FPGA实现 *
摆玉龙,潘星宇,段济开,杨 阳
(西北师范大学物理与电子工程学院,甘肃 兰州 730070)
1 引言
1971年,美籍华人蔡少棠教授根据电路理论的完备性,提出了电路中应该存在一种无源器件,它能反映磁通量与电荷之间的关系,并称这种元件为忆阻器(Memristor)[1],但是,忆阻器在当时并没有引起人们的重视。直到2008年,HP公司采用纳米技术成功研制了世界上首个忆阻器[2]。它的研制成功引起了社会的广泛关注,引发了忆阻器的研究热潮。忆阻器本质上是一个具有记忆功能的非线性电阻,文献[3]利用电压控制浮地阻抗电路和电流积分器设计了一种忆阻器模拟器,通过PSpice仿真发现它可以很好地反映忆阻器的非线性特性;文献[4]详细地研究了HP公司的忆阻器模型,并对P型和N型忆阻器的串并联网络进行了详细的分析,发现当2个参数对偶的忆阻器串联时呈现线性特性,但仍保持记忆特性。正是由于忆阻器具有非线性和记忆2个特性,使得忆阻器在阻变存储器[5,6]、现场可编程逻辑门阵列[7]、人工神经网络[8 - 10]、混沌系统[11 - 14]、图像处理[15,16]和语音处理[17]等领域中发挥着越来越重要的作用。
近些年来,混沌系统的分析与设计正在稳步快速发展,除了经典的Lorenz系统[18]、Chen系统[19,20]和Chua系统[21]等外,一些新的混沌系统[22,23]也相继被提出。这些系统一般都是通过增加或者改变系统的乘积项来实现的,但是在通信加密领域,动力学行为越复杂的混沌系统加密性能越好,抗破译能力越高。为了满足这方面的需求,研究者们采用经典的反馈控制法来设计更复杂的混沌系统。常用的反馈方式有线性反馈和非线性反馈,其中非线性反馈的复杂程度强于线性反馈。然而,传统的非线性反馈都采用的是四象限乘法器和运算放大器等元件与电阻、电容和电感配合实现,该方法设计的电路比较复杂,实现较困难。而忆阻器本身就是一种无源的非线性元件,这使得混沌系统的设计难度大大降低,再加上它对流过的电流具有记忆功能,这也是常规元件所不具备的性能。
由于忆阻器的实际物理模型还难以实现,对它的研究主要是在理论模型上,一般来说,其模型主要有2类:一种是三次光滑模型,另一种是分段线性模型。文献[15]提出了一种基于双曲正弦函数的忆阻器模型,分析了电压与流经其2端电流的关系特性,发现该模型具有忆阻特性。本文利用该模型,采用正反馈设计了一个四维的具有4个翅膀的忆阻混沌系统,通过数值仿真实验绘制了系统各个平面的相图、Lyapunov指数谱和分岔图等,对系统的稳定性和动力学特性做了详细的分析,最后利用FPGA与数模转换器(DAC)设计了电路,利用数字示波器观察其结果与数值结果基本一致。
2 双曲正弦忆阻模型
本文采用的忆阻器模型为文献[15]提出的双曲正弦函数磁控忆阻器,如式(1)所示:
(1)
其中,φ为磁通量,q(φ)为电荷,W(φ)为忆导。对该模型施加了一个正弦电压作为激励,利用四阶龙格库塔算法求解该模型得到其伏安特性曲线,如图1所示,发现该模型所得到的电压与电流关系为一条斜“8”字形类紧磁滞回线,其结果与文献[2,15]中描述的电压电流关系基本一致。
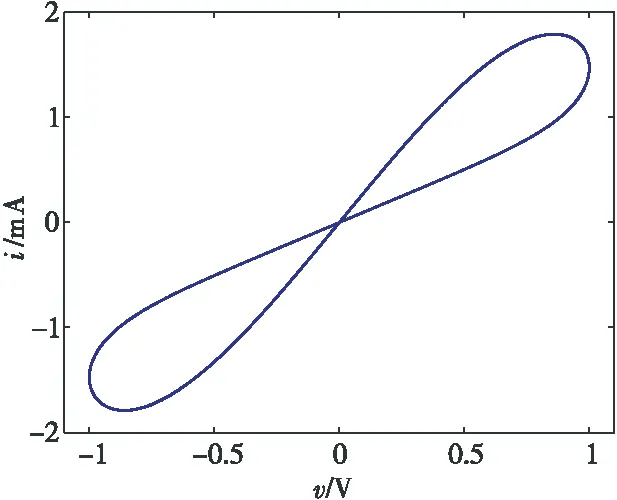
Figure 1 V-A relationship of memristor图1 忆阻器V-A关系
3 四翼忆阻混沌模型
本文提出的忆阻混沌系统是在一个三维混沌系统的基础上通过添加一个忆阻器作为正反馈项来实现,具体模型如式(2)所示:

(2)
其中x,y,z和u为系统的状态变量;W(φ)=cosh(ηu);α,β,γ,σ和η为系统参数。选取系统的初始条件为x0= 0.1,y0= 0,z0= 0.1,u0= 0,仿真步长为0.001,采用四阶龙格库塔算法对该系统进行数值实验发现,当α=10,β=28,γ=20,η=0.2时,系统存在一个吸引子,该吸引子在x-y,x-z,y-z和z-u平面的投影如图2所示。

Figure 2 Chaotic attractor图2 混沌吸引子
当初始值发生微小的改变时,仿真之后发现混沌现象消失,不存在混沌吸引子。当系统参数发生变化时,系统的稳定性和运动状态等特征也随之变化,这就是混沌系统对于初始值和初始条件的高度敏感性。为了研究系统的特征,本文将对该系统的稳定性和动力学特性进行分析。
3.1 系统特性分析
(1)耗散性。
系统的散度如式(3)所示:
(3)
当α=11,γ=20时,▽V= -30<0,因此该系统为耗散系统,即系统整体是稳定的且相体积会以一定的速率收缩,最终达到平衡态。
(2)平衡点与稳定性。

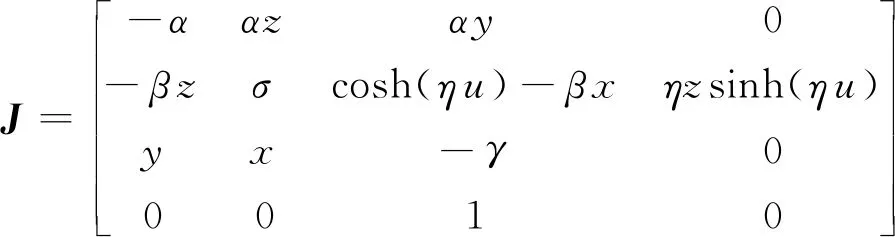
(4)
则平衡点集A的特征方程如式(5)所示:
λ[λ3+(α+γ-σ)λ2+
(αγ-σ(α+γ))λ-αγσ]=0
(5)
由式(5)得到系统有一个特征值λ1=0,还有3个非0特征值分别为:λ2=1,λ3=-11,λ4=-20,相应的特征向量为e1=[0,0,0,1],e2=[0,1,0,0],e3=[1,0,0,0],e4=[0,0,1,0]。根据特征值与特征向量,系统在x方向上不稳定,在y方向和z方向上稳定,在z-u方向上系统临界稳定,平衡点E为鞍点。也就是说系统相轨迹在x方向发散,y和z方向收敛的共同作用下,出现了如图2所示的混沌吸引子。
3.2 动力学特性分析
为了进一步研究系统复杂的行为,对其进行动力学分析。
(1)Lyapunov指数。
混沌对初值具有高度敏感性,为了反映其对初值的敏感程度,采用Lyapunov指数来描述它。Lyapunov指数反映了动力学系统相空间中轨迹的整体行为,也就是说只要系统存在一个正的Lyapunov指数,系统中任何相邻的2条轨道必然会以指数速率分离而进入混沌状态,因此,通过计算该指数可以判断系统是否为混沌系统,其定义如式(6)所示:
(6)
其中,δxi(0)为t=0时相邻2条轨道的差,LEi表示第i个坐标方向的Lyapunov指数。保持系统参数不变,利用Wolf方法[16]计算系统的Lyapunov指数为LE1=0.4384,LE2=0.0364,LE3=0.0299,LE4=-30.4449。发现系统存在正的Lyapunov指数,表明系统处于混沌状态,且LEall=-30<0,说明该系统的相体积整体上是收敛的,这与前面提到的系统散度的结论一致,即系统整体稳定。固定其他参数不变,选取σ∈(0,13),步长为0.013,时间步长为0.5 s,时间为100 s,初始值设为(0.1,0,0.1,0)时,Lyapunov指数谱和z平面的分岔图分别如图3和图4所示。
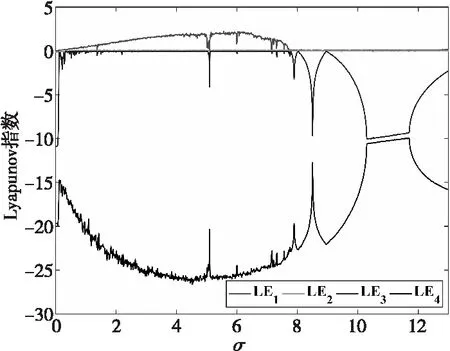
Figure 3 Lyapunov vs. parameter σ图3 参数σ变化时的Lyapunov指数

Figure 4 Bifurcation diagram of parameter σ vs. variable z图4 z变量随参数σ变化的分岔图
对比发现,Lyapunov指数图与分岔图基本保持一致。当σ=0时,最大Lyapunov指数为负,此时系统做周期运动;当σ∈(0,7.748)时,系统由周期运动进入混沌状态,在此区间内系统的最大Lyapunov指数均为正;当σ∈(7.748,13)时,2个Lyapunov指数等于0,2个Lyapunov指数小于0,系统进入拟周期运动状态,即出现极限环。分别取σ为0,7,9,12时,系统在y-z平面的投影如图5所示。
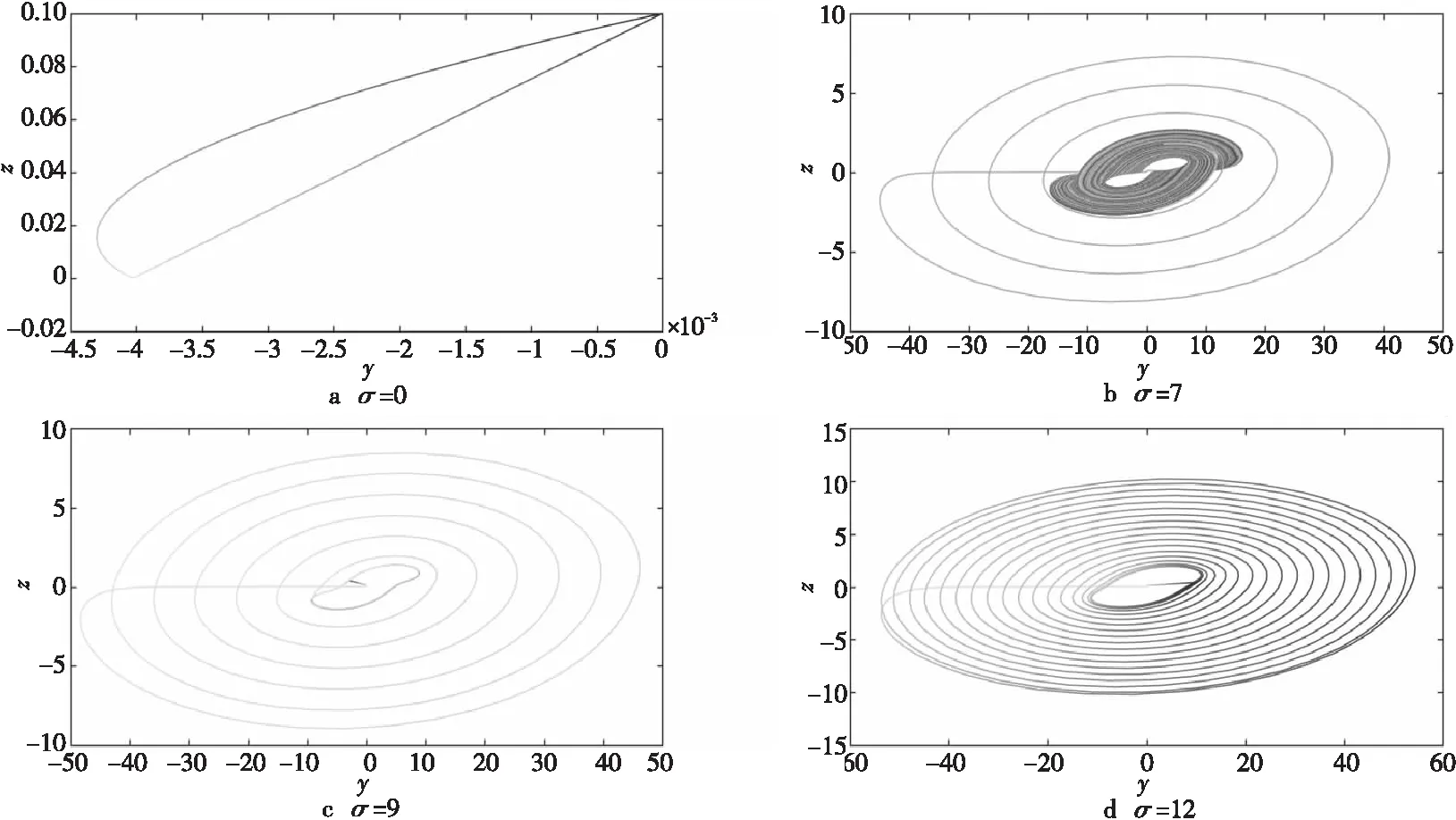
Figure 5 y-z plan phase spectrum of parameter σ图5 参数σ变化时y-z平面相图
可以看到,当σ取0时,系统为周期运动;当σ取7时,系统进入混沌状态;当σ取9和12时,系统由混沌退化到极限环,其结果与Lyapunov指数谱和分岔图的结果一致。
4 FPGA实现
本文设计的混沌系统基本原理如图6所示,利用FPGA定制一个32位的软核CPU NIOS II,通过Avalon总线与片上外设的IP核进行数据交换;DAC的IP核驱动DAC输出混沌信号;ROM IP驱动Flash芯片保存程序代码;RAM IP驱动外部的SDRAM保存运算过程中的临时数据;PLL IP将外部晶振提供的50 MHz时钟倍频为2路相位相差-75度的100 MHz时钟,一路作为CPU时钟送至NIOS II,另一路作为存储器时钟送至外部SDRAM;JTAG IP用来下载和调试程序。选用的FPGA为Altera公司的Cyclone IV EP4CE6F- 17C8N芯片,DAC选用德州仪器的程控12位双通道TLC5618A,开发环境为英特尔的Quartus Prime 18.0,软核与片上IP采用Platform Designer开发,其中NIOS II CPU类型设置为Float型,其内部集成了硬件乘法器,有利于提高运算速度。
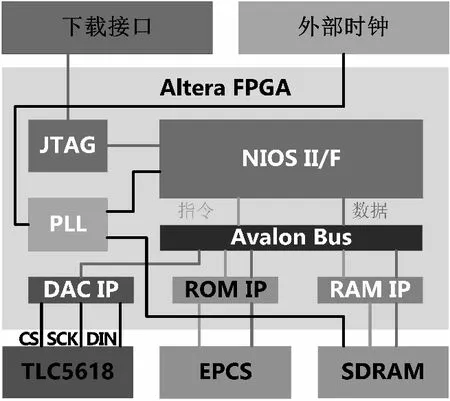
Figure 6 Schematic of FPGA chaotic system图6 FPGA混沌系统原理图
考虑到龙格库塔算法会占用FPGA大量的逻辑资源,因此选用欧拉算法来减小运算量,对系统式(2)进行离散化得到式(7):
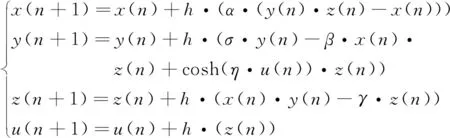
(7)
其中,h=0.001为步长。将式(7)转化为C代码,经过编译、综合、分配引脚后,下载至FPGA,最后通过数字示波器得到系统的时域波形图和x-z平面的相图分别如图7和图8所示。可以看到该结果与数值结果基本一致。
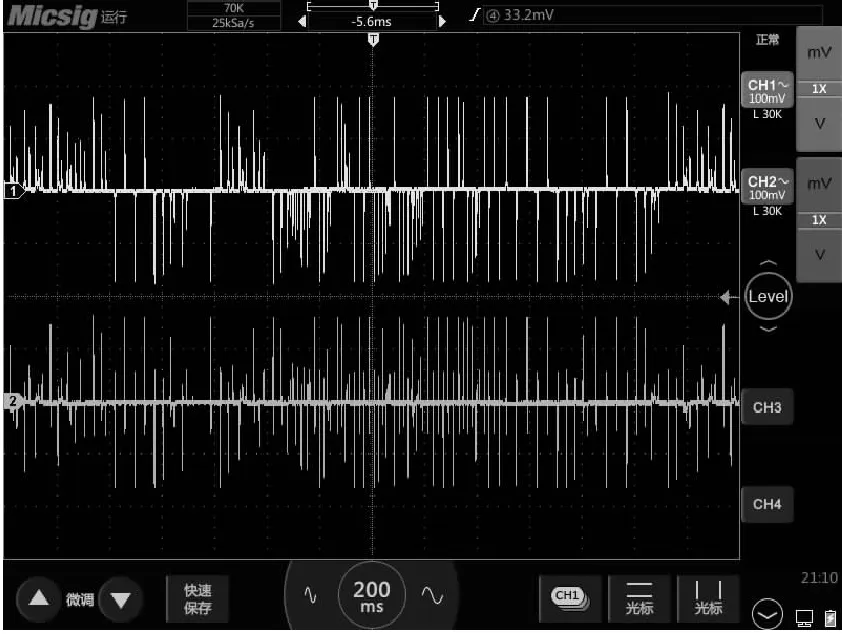
Figure 7 Time domain wave form on the oscilloscope图7 示波器时域波形图
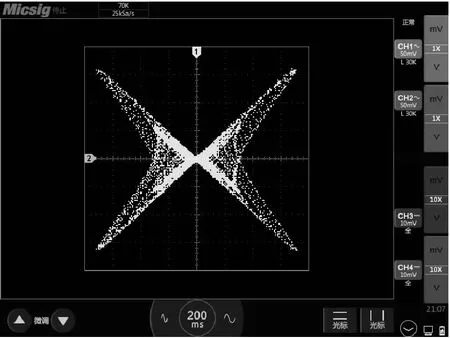
Figure 8 x-z plane phase diagram on the oscilloscope图8 示波器x-z平面相图
5 结束语
本文基于双曲正弦函数的忆阻器模型作为正反馈设计了一种新的忆阻混沌系统。通过数值仿真发现系统出现4个翅膀的混沌吸引子,接着对系统的耗散性、平衡点和稳定性进行分析,发现该系统为耗散系统且只有一个平衡点,且该点为鞍点,由于系统在平衡点处不稳定而出现了混沌吸引子,为此对系统进行了动力学特性分析,研究了系统随着参数变化时其运动形态的变化情况。最后,利用FPGA设计了混沌电路系统,验证发现其结果与数值结果基本一致。

