快速卷积算法的综述研究 *
李 创,刘宗林,刘 胜,李 勇,徐雪刚,夏一民
(1.国防科技大学计算机学院,湖南 长沙 410073;2.湖南长城银河科技有限公司,湖南 长沙 410000)
1 引言
随着深度学习的蓬勃发展,研究人员对卷积神经网络CNN(Convolutional Neural Network)的研究工作[1 - 3]将会把重心放在更大规模和更高准确率上,在卷积神经网络中,更大规模和更高准确率需要更快速更准确的运算,所以研究卷积神经网络的加速方法很重要。与此同时,针对卷积神经网络的加速优化近年来也有了快速的发展,如低秩分解、定点运算、矢量量化、稀疏表示[4]、剪枝[5]和快速卷积[6 - 10]等,实现了卷积神经网络整体的加速效果。在一个卷积神经网络[11]中,卷积是核心,同时运算量最大的部分也是卷积部分,未来计算力的强弱将会决定神经网络的发展速度。更大的计算规模、更丰富的数据、更高强度的计算依然是深度学习的下一个发展点,卷积神经网络能否在众多应用中继续体现出巨大优势,这将依赖于更强的计算能力。而卷积神经网络的计算量绝大多数集中在卷积操作的乘加操作上,这些巨大的计算量和惊人的功耗极大地限制了卷积神经网络应用的发展,也限制了研究人员的研究进度。卷积加速的研究工作意义非凡,在迫切需求更强计算力的未来,卷积加速的研究工作有待进一步加深。目前对于卷积优化的方法也有很多,因此本文将对近年来常见的卷积加速方法做一个总结。
2 概述
2.1 卷积
在CNN中,卷积是图像处理中最基本又是最重要的操作。卷积是待处理的图像和卷积核两者之间发生的操作,对于待处理图像中的每一个像素点计算它周围像素点和卷积核矩阵的对应像素点的乘积,然后把乘积结果累加到一起,作为输出特征图的像素点,具体过程如图1所示,这样就完成了卷积过程。准确地说卷积有3种模型,分为Full卷积、Same卷积和Valid卷积,卷积时,卷积核是在卷积图像上进行滑动,Full卷积指的是从卷积核滑动到和图像刚相交时就开始进行卷积,Same卷积指的是卷积核中心滑动到和图像刚相交时就开始进行卷积,Valid卷积指的是卷积核滑动到如图1所示位置处开始进行卷积。

Figure 1 Process of convolution图1 卷积的过程
引入现实中卷积应用的意义,可加深对卷积运算的理解。物理学中的信号处理过程,信号的输出不仅仅受t时刻的输入响应影响,还受到t时刻之前的输入响应影响,不过t时刻之前的影响相对于t时刻有一定衰减,所以t时刻的真实输出应该是所有时刻响应的叠加,同时由于不同时刻的影响不同,不同时刻的影响应该乘以一个系数,这整个过程就是卷积。
图1卷积过程需要36次乘法和32次加法操作,随着输入图像尺寸的增大以及通道数的增加,卷积运算所需的乘加次数也在倍增。可以看出,卷积操作会占用卷积层乃至整个网络执行时间的绝大部分,目前针对卷积操作的优化实现也有了初步的进展,但是随着计算机体系结构的发展,优化工作需要继续展开,根据不同的体系结构实现不同的优化方法。
图像直接卷积运算的本质是若干个子矩阵块与卷积核的卷积。卷积图像可划分成若干和卷积核大小一致的小块,块和卷积核的运算如算法1所示,而图像直接卷积是最传统的计算方法,其实现见算法2。算法2中M是本层输出的特征图尺寸,K是卷积核尺寸,C_in是输入图像的通道数,Kernel_num是输出特征图的通道数,kernel为卷积核的尺寸,在卷积神经网络中,单层的时间复杂度为O(M2*K2*C_in*Kernel_num)。Matlab中的conv函数实现以及cuda-convnet2函数的实现采用的就是直接卷积方法,这种直接卷积方法效率不是特别高,所以研究人员对该卷积加速运算进行了进一步的研究。
算法1Block_Conv
Input:Block,Kernel。/*Block,Kernel分别是2D多通道图像的1个小块和卷积核*/
Output:y。//y是块卷积的输出
Fork=0;k Fori=0;i y=Block[k][i] *Kernel[k][i]; Returny 算法2Image_Conv Input:Img,Kernel。/*Img,Kernel分别是2D多通道图像和卷积核*/ Output:Y。//Y是输出图像 Form=0;m Forn=0;n Forc=0;c Forr=0;r Y[r][m][n]+=Block_Conv(Img[c][m][n],kernel) ReturnY 卷积操作是卷积神经网络中耗费时间最长的部分,因为计算涉及到多次乘加运算。在任何一个卷积神经网络中,每一卷积层对图像信息进行卷积处理时,其计算量可表示为输出特征图的大小和参数量的大小的乘积,例如:当卷积核的尺寸为5*5*3,卷积核的个数为2时,卷积核的参数量为 5*5*3*2,偏差的参数量为2,输入图像尺寸为28*28*3,无填充,且步长大小为1,则按照式(1)计算得到卷积后的输出特征图尺寸为24,输出特征图的数量为2。 Out_map=In_img+2*pad- kernel/Strides+1 (1) 其中,Out_map是输出特征图的尺寸,In_img是待处理图像的尺寸,pad是填充尺寸,kernel是卷积核的尺寸,Strides是步长。 这一层卷积操作所需要的计算量为(5*5*3*2+2)*(24*24)=87552。所以,卷积操作占了执行时间的绝大部分。目前针对卷积操作的优化实现也有了初步的进展,但是随着计算机体系结构的发展,优化工作需要继续展开,根据不同的体系结构设计不同的优化方法。 CNN主要由卷积层、池化层和全连接层构成,其中卷积层用来提取图像特征,池化层用来降维减少运算量,全连接层用来输出分类。CNN的大部分计算量集中在卷积层上,而随着深度学习的发展,研究人员正采用更多卷积层的复杂模型来提高预测精度,这些模型的巨大计算量和惊人功耗限制了CNN在嵌入式设备的广泛应用。因此,加速卷积算法正成为近期研究的一个热点。 CNN在计算机视觉领域有着非常广泛的应用,常用来进行图像的识别与分类、图像分割、目标检测与定位、图像生成等。词向量的引入,使得CNN可以在机器翻译、文本分类、语音识别等自然语言处理领域得以应用。生活中常见的自动驾驶技术、美颜、人脸识别打卡等都是基于CNN设计的,Facebook提出的CNN机器翻译,在当时比谷歌的翻译快9倍。 通过查看当前主流的深度学习框架,就能知道目前主流的卷积层优化算法,在Caffe中卷积层采用的是img2col+GEMM(GEneral Matrix Multiplication)算法,PaddlePaddle中卷积层使用的是Winograd算法,而Facebook曾经的NNPACK(acceleration PACKage for Neural Network computations)中的卷积实现和LightNet中的CNN实现采用的都是基于快速傅里叶变换FFT(Fast Fourier Transform)的算法。这3种算法是目前最为流行的针对卷积层进行加速的加速算法。 img2col是用来优化卷积运算的一个重要算法,Caffe框架的卷积实现就是采用的这种方法。传统卷积运算时,根据不同的卷积核大小需要不断地从卷积图像矩阵中取出和卷积核同样大小的卷积块,使用for循环来实现卷积,遇到卷积图像尺寸过大时,需要多次访存,非常耗时。img2col算法的核心思想是把图像感受野部分转换为一行或一列来存储,减少内存访问次数,从而达到优化卷积运算的目的。从另一方面来讲,当img2col把卷积图像信息做完转换后,可以把感受野部分转换后的若干行或若干列拼成矩阵,对于卷积图像而言,拼成的矩阵的行数或者列数就是卷积核在卷积图像上滑动的次数。img2col算法的转换过程如图2所示。卷积图像被转换为新矩阵后卷积运算就变成了矩阵相乘运算,辅以现有的矩阵乘优化库可以明显地加快卷积速度。 Figure 2 Principle of img2col图2 img2col的原理 GEMM在深度学习中发挥着十分重大的作用,卷积神经网络中的全连接层和卷积层的运算都可以用矩阵乘来实现,而一个卷积神经网络中90%的运算量都集中在全连接层和卷积层,优化GEMM可以实现对卷积神经网络的加速。GEMM卷积算法如算法3所示,其中A和B是用img2col算法转换后的卷积图像和卷积核矩阵,A是一个R*C的矩阵,B是一个C*K的矩阵,R为输出矩阵的宽和高的乘积,C为卷积核宽和高的乘积,K为卷积核的数量。 算法3GEMM_Conv Input:A,B。 Output:C。 Form=0;m Forn=0;n Fork=0;k C[m][n]+=A[m][k] *B[k][n]; ReturnC img2col+GEMM实现卷积操作是目前计算卷积的常用方法之一。可以利用GEMM的优化来实现对卷积的优化,目前现有的矩阵优化技术已经可以将常见的矩阵乘运算改进约7倍。按照传统卷积的方式,参与运算的数据在内存中的存放是不连续的,因此需要多次访存。为了解决该问题,研究人员提出了img2col,可以节省访存的时间,从而达到加速的目的。img2col把卷积操作转换为矩阵乘后,使用优化后的GEMM可以实现进一步的加速。从图2可以看出,卷积图像的信息被多次复用提取到转换后的矩阵中,增加了额外的内存开销,以Lenet网络模型的第1层卷积为例,输入图像大小为32*32,6个5*5的卷积核,输出6个28*28的输出特征图信息,用img2col把输入信息转换为维度为(28*28)*(5*5)的矩阵,相较于原始的32*32的图像输入信息所占用的内存,转换后的矩阵信息所占用的内存高达18倍以上。 img2col+GEMM能将复杂的卷积过程转化为矩阵相乘的简单运算,不仅适用于二维卷积,还可推广到三维甚至更高的维度,具有很好的通用性。 Winograd算法早在1980年就被提出用来减少有限长单位冲激响应FIR(Finite Impulse Response)滤波器的计算量,同FFT一样都需要把数据变换到其他空间进行处理后再变换回原空间,不同于FFT的是Winograd变换不涉及复数。在2016的CVPR会议上,Andrew等[7]提出的快速算法就使用了Winograd进行卷积加速。目前腾讯的NCNN(Neural Network Inference Computing Framework)、Facebook的NNPACK和NIVDIA的cuDNN(NVIDIA CUDA Deep Neural Network)中计算卷积的算法都是采用的Winograd算法。 Andrew等[7]对Winograd算法做卷积运算做了很大篇幅的介绍,其中一维Winograd算法需要进行3次线性变换,具体转换过程如式(2)所示,二维Winograd算法需要6次线性变换,具体实现过程如式(3)所示: Y=A′[(Gg)⊙(B′d)] (2) Y=A′[(GgG′)⊙(B′dB)]A (3) 其中,☉表示点乘,A′表示矩阵A的转置,用来对结果做线性变换,B′表示矩阵B的转置,用来对输入信息进行线性变换,G是用来对卷积核做线性变换处理的变换矩阵,g是卷积核数据,d是输入数据。 一维Winograd算法中的A,B′,G如下所示: 大部分卷积神经网络加速器都采用的卷积加速算法就是Winograd算法,它是Strassen算法的变形。Strassen算法是一种通过减少矩阵相乘中的乘法次数来实现矩阵相乘的矩阵相乘优化算法,关于Strassen算法不作过多介绍,可参考文献[12],它把矩阵乘法的算法复杂度由O(n3)降低到了O(n2.81)。Winograd的相关算法也是从减少矩阵相乘算法中的乘法次数来实现卷积计算的加速效果,2011年研究人员已经利用Winograd算法把矩阵相乘算法的复杂度降低到了O(n2.3727)。Winograd算法已经在深度学习的大部分应用中显示出较大的优势,成为当前最常用的卷积加速算法之一。 Andrew等[7]对Winograd算法的卷积运算进行了很大篇幅的介绍,目前主流的加速器对于卷积操作的加速大部分都采用的是Winograd快速卷积算法。Winograd快速卷积算法利用了卷积图像像素点之间的结构相似性,运用恰当的数学技巧将乘法运算转换为加法运算,因此能降低算法复杂度,实现卷积加速。 对于一维Winograd卷积,当输出长度为m,卷积核长度为r,所需要的乘法数量是m+r-1,相较于不使用Winograd算法时的m*r次乘法,Winograd算法带来了性能上的提升。输入信号为d=[d0d1d2d3],卷积核g=[g0g1g2]时,其卷积如式(4)所示: (4) 其中: m0=(d0-d2)g0, m2=(d1-d3)g2, 在Winograd算法中,所需的乘法次数为2+3-1=4次,直接运算需要6次乘法,而且卷积核部分的数据加法在训练时只需计算1次,在推理过程中可以省略,整体的运算量下降,从而实现了加速。Winograd快速卷积算法可以被推广到二维,基于分块矩阵的思想,先把输入图像矩阵展开成大矩阵形式,划分成一维的形式,进行进一步的处理。将一维卷积扩展到二维卷积,二维的F(2*2,3*3)需要16次乘法,而原来的算法需要进行36次乘法,乘法次数减少了36/16倍,加速效果更明显,二维的Winograd卷积加速算法可见文献[7]中的算法1。 采用Winograd算法做卷积,相较于直接卷积的6层循环,里面2层循环可以设计Winograd计算模块来替代,Liang等[13]介绍了Winograd算法在FPGA上的实现,在他们的研究成果中调用设计好的Winograd计算模块,就可以直接计算出卷积参数,减少了50%以上的乘法操作,F(2*2,3*3)的Winograd卷积算法具体实现步骤如下所示: 第1步:滑动提取一个tile(即提取每幅图像上的一小块数据)直至遍历完输入图像信息,tile大小选择4*4; 第2步:对提取的tile做线性变换; 第3步:对卷积核做线性变换; 第4步:对变换后的卷积核和tile做点乘; 第5步:对第4步的输出结果做线性变换,循环执行。 二维的Winograd卷积算法的复杂度为O(M2*C_in*C_out),其中C_out表示输出通道数。在实际中使用Winograd算法做卷积时,减少乘法次数是以增加加法次数为代价,同时额外的转换计算也会增加算法的整体运行时间,所以多方面的代价需要我们在选择Winograd算法实现卷积加速时进行综合考虑。 从2.1节算法1的介绍中可以看出,卷积的本质是块与卷积核之间的计算,所以可以通过对算法1进行加速来加快整个图像卷积的计算速度。快速傅里叶变换FFT是离散傅里叶变换的快速算法,能加快多项式乘法的运算速度。1965年,Cooley等[14]提出了FFT算法,节约了计算机的计算处理时间,普通多项式乘法的时间复杂度为O(n2),而FFT能让多项式乘法在O(nlbn)的时间内完成运算,所以,在算法1的计算中,可以利用FFT来实现加速。 卷积定理指出函数卷积的傅里叶变换是函数傅里叶变换的乘积,这个定理是傅里叶变换满足的一个重要性质,关于卷积定理的证明可参考文献[15],卷积定理为FFT能在深度学习领域进行卷积加速运算提供了可能性。Mathieu等[16]曾在2014年ICLR会议上提出了用FFT加速卷积网络训练的方法,并且在当时的卷积运算方面有着1个数量级以上的改进。关于FFT做卷积运算的研究已经开展了很多年,相关研究[17]取得了一定的进展,也已经获得了很大的性能提升,基于Matlab的轻量级深度学习框架LightNet[18]、Facebook的NNPACK框架和CUDA的cuDNN等,都支持基于FFT实现卷积。目前的研究工作中,经常使用一维和二维序列的FFT变换操作。无论是一维还是二维FFT实现快速卷积,其主要步骤相同,只是在进行FFT变换时有所不同,执行1次二维FFT变换相当于2次一维FFT变换。利用FFT实现一维快速卷积的算法如算法4所示,其中,“.*”符号表示对应位置元素相乘。 算法4FFT_Conv Input:卷积图像序列X和卷积核序列Y,长度分别为S和N。 Output:Res。 L:L满足L≥S+N-1,且L是2的幂次方; Form=S;m X[m]=0; EndFor∥补零 Forn=N;n Y[n]=0; EndFor∥补零 Res=ifft(fft(X).*fft(Y)); ReturnRes 当FFT变换的点数为n时,FFT做卷积的复杂度为3次n点FFT计算与n次乘法,即为3*O(nlogn)+O(n),所以本算法的复杂度为O(nlogn)。利用FFT实现一维卷积[19 - 21]时,当FFT的变换点数L越大时,加速效果越明显,L越小加速效果就越差。在一些嵌入式平台上,有相应的硬件支持,FFT快速卷积的效率更高,文献[22 - 24]探索了在微处理器平台上实现FFT卷积的性能,研究表明内置的FFT指令能进一步对卷积运算进行加速。FFT卷积实现了一定程度上的卷积加速,但是其依然存在一些缺陷,在卷积神经网络中有一定的限制,因为在卷积神经网络中,卷积核的尺寸很小,比如VGG(Visual Geometry Group)里面大小为3*3和5*5的卷积核非常多,在这种情况下,卷积图像大小和卷积核尺寸大小相差很大,再使用FFT实现卷积,需要在用FFT进行变换时补零,开销加大,使用FFT实现卷积就有点得不偿失。 利用时域卷积等于频域乘积的性质,用FFT进行快速卷积运算,这里以二维FFT做卷积为例,FFT 1次变换和IFFT(Inverse Fast Fourier Transform)1次变换需要的计算量都为O(2M2*logM),FFT实现卷积需要对卷积图像、卷积核和输出进行转换,所需要转换的数量分别为(单批次)C_in,C_out和C_out*C_in,FFT变换所需要的总计算量为2M*M*logM*(C_out+C_in+C_in*C_out),变换之后的张量之间(复数)的乘积所需要的计算量最少为4*C_in*C_out*M*M,所以FFT实现卷积需要的总计算量为O(2M2*logM*(C_out+C_in+C_in*C_out)+4*C_in*C_out*M*M)。 FFT变换是一种线性变换,不会影响多通道变换后的结果,能节省出很大一部分开销。FFT变换会增大内存带宽需求,占用大量内存,与此同时,对于卷积步长大于1的卷积操作,由于数据比较稀疏,这种情况下利用FFT做卷积的效率也很低。 为了解决FFT卷积在卷积核过小而输入图像数据过大时不适用的问题,Lin等[25]提出了一种tFFT(tile Fast Fourier Transform)算法,实现了CNNs傅里叶域的基于tile的卷积,对于卷积核比较小的情况,可以进行批量FFT运算,通过隐藏数据读取时间,复用旋转因子,提高FFT的计算效率。在对卷积神经网络进行训练时,会有成千上万次卷积运算,为了利用FFT进行加速训练和推理该tFFT算法是针对FFT做卷积加速时不适用较小的卷积核这一问题提出的一种新算法,引入了tile分解的方法对经典的FFT进行扩展,使其能适用小卷积核的情况,达到加速卷积运算的目的。tFFT的实现过程大致如下:首先将大尺寸输入在逻辑上划分为与滤波器核大小相近的块,然后在傅里叶域中对这些逻辑上划分的块和滤波器进行转换。其次,递归地将之前的分块输入分解为蝴蝶运算,这些蝴蝶运算操作在GPU的并行流上进行计算。在批大小为128以内,相较于经典FFT卷积算法,tFFT在ResNet-34模型上的平均算法复杂度降低到原来的1/3左右,在VGGNet-19模型上的平均算法复杂度降低到原来的1/4左右,在AlexNet模型上的平均算法复杂度降低到原来的1/4左右。 Budden等[26]提出了一种快速张量卷积算法。同Winograd算法类似,快速张量卷积也是通过减少乘法次数来减少计算量的卷积算法,该算法引入中国剩余定理的思想,不需要生成Winograd卷积算法的转换矩阵,并且可在高维上实现卷积运算。同时,Budden等[26]也引入了在多核上实现深度加速的方案,利用多核处理器高度并行的能力,对卷积运算进行深度加速,在性能上获得了可观的效果。 基于常见的GEMM卷积算法和Winograd卷积算法,Kala等[27]提出的一种变体算法研究了在Winograd算法基础上结合GEMM的实现方案。 而基于常见的FFT卷积算法和Winograd卷积算法,文献[28]提出了Winograd和FFT融合方案,便于数据处理。 Winograd算法是目前最实用的快速卷积算法,在各大深度学习框架可以看到大量的研究工作者不约而同地都在使用Winograd算法,针对Winograd快速卷积算法的研究,延伸出了多种变体算法,除了上述几种外,文献[29]提出了一种改进算法,能够对更长序列的卷积网络进行加速;文献[30]提出了一种基于积分的卷积核缩放方法,可以使最终的结果没有太大的精度损失,文献[30-37]等都是融合了Winograd快速算法的思想。 基于额外内存占用问题,文献[38-40]等提出了优化内存与速度的卷积计算方法,尽可能减少内存消耗。 前文提到的多种快速卷积算法多数都是从运算技巧上入手,通过减少运算次数实现加速优化,从减少参数运算量的方面,也可以加速卷积运算。对参与卷积运算的卷积核进行分解,可以显著降低参数量,以7*7的卷积核为例,可以用3个3*3的卷积核替代实现相同的效果,前者需要的参数量为49,后者需要的参数量只有27,降低了40%以上的参数量,能实现卷积的快速运算,此外模型压缩、量化等都是从降低参数量的方面实现对卷积的优化。 CNN最终要部署在计算设备上来完成图像识别、语音识别和自然语言处理等任务,涉及到具体的实现,就要根据计算设备的特性来实施部署的方案。每一幅特征图的卷积运算可以被分解为若干幅小特征图和卷积核的浮点乘加计算,这些运算过程是相对独立的,不存在先后顺序和相互影响,可以利用并行处理来实现加速。根据目前CNN使用状况,使用者常把CNN部署在CPU或者GPU上运行进行训练和推理,将CNN部署在移动终端上完成推理任务在近年来也得到了很多关注: (1)基于GPU的CNN加速。GPU是专为执行复杂的数学和几何运算而设计的,具有大量的计算核心,适合大规模的并行运算,当前GPU在CNN中占有重要的地位。Andrew等[7]在实现Winograd算法时,使用VGG网络模型,实验测试相比cuDNN,Winograd算法在不同批次不同浮点数位数时都有一定的性能提速,且最高提速达到了7.42x。Mathieu等[14]从算法复杂度方面详细论述了FFT卷积算法的优势,而使用CUDA能方便地利用计算平台提供的cuFFT来实现卷积计算。如图3展示了FFT卷积和直接卷积所需要的运算操作次数,其中,n是参与FFT的点数,纵轴是所需操作数,量级是1010。CUDA是NVIDIA推出的运算平台,它能提供丰富的函数接口,利用CUDA可以方便快速地实现卷积。针对特定领域的应用,CUDA为开发人员提供了多种多样的库,包括针对深度学习领域的库[36],其中cuDNN[41]是NVIDIA开发的用于深度学习网络的GPU加速库,利用cuDNN可以方便地实现各种卷积算法,研究人员可以对卷积算法进行快速的验证对比,使研究人员更多地专注于神经网络结构的层次,而不用过多地思考性能问题。 Figure 3 FFT convolution versus direct convolution performance on GPU图3 GPU上FFT卷积和直接卷积的对比 (2)基于CPU的卷积加速。现在CPU多数都具有多个CPU核心,而目前很多程序都没有进行过多核优化,因此对程序进行并行设计,尽量使用多线程处理,可以充分利用CPU的硬件资源,提高算法的执行效率。David 等[42]基于CPU硬件扩展了Winograd类的卷积算法,使其能在高维上进行有效卷积计算,并通过向量化处理加速卷积计算,利用多核并行充分发挥CPU的硬件性能,相比以前的先进水平,有着5~25倍的吞吐量提升。Jia 等[43]从数据布局、数据转换和批量矩阵乘法等方面出发,在CPU硬件上实现了Winograd类卷积算法,相比其他种类卷积,有着3倍的性能提升。 (3)基于移动终端的CNN加速。用户需要将CNN部署在手机、无人机和汽车等移动终端上,完成图像分类、识别,目标检测与定位,人脸识别等任务,考虑到便携性和成本,存在存储资源和计算资源有限的问题,导致在移动设备上无法部署规模较大的网络,轻量级模型和模型压缩是解决存储限制和降低功耗的有效方法之一。 卷积神经网络需要大量的数据来保证较高的准确率,所以计算速度在近年来一直是研究人员所关注的重点,无论是自动驾驶,还是医学分析亦或其他的应用领域,都需要快速地响应处理,这都依赖于更快的计算速度。对卷积运算进行加速,无疑是一种对网络模型进行高度加速的有效途径。前文论述的几种快速卷积算法,各有利弊,很多时候研究人员使用的是这些算法的综合变体算法,未来卷积加速工作的重心将会放在更小卷积核与更大的卷积图像信息的卷积加速上,FFT的一些变体算法,以及Winograd的卷积核尺寸多变算法等将成为卷积加速研究的主流。2.2 卷积神经网络应用
3 快速卷积算法
3.1 img2col+GEMM

3.2 Winograd卷积算法
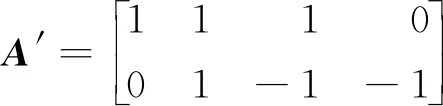

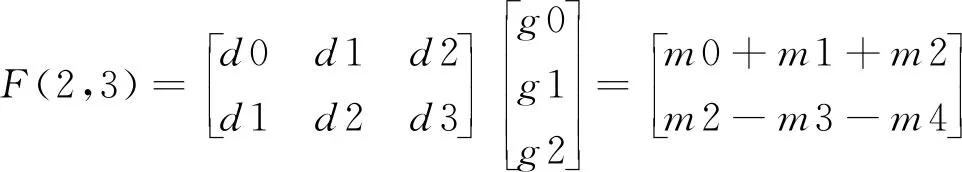
3.3 FFT卷积算法
3.4 其他快速卷积算法
4 具体实现

5 结束语

