具有相似性传播的K-均值欠定盲分离算法 *
何选森,徐 丽,夏 娟
(1.广州商学院信息技术与工程学院,广东 广州 511363;2.湖南大学信息科学与工程学院,湖南 长沙 410082)
1 引言
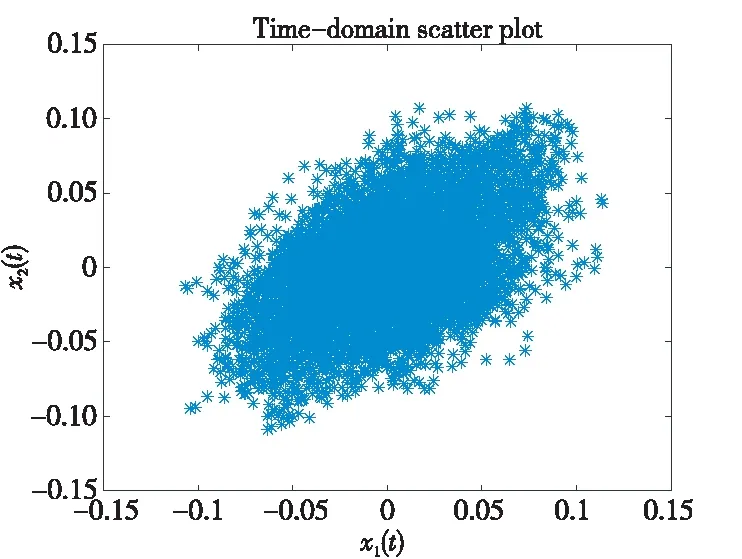
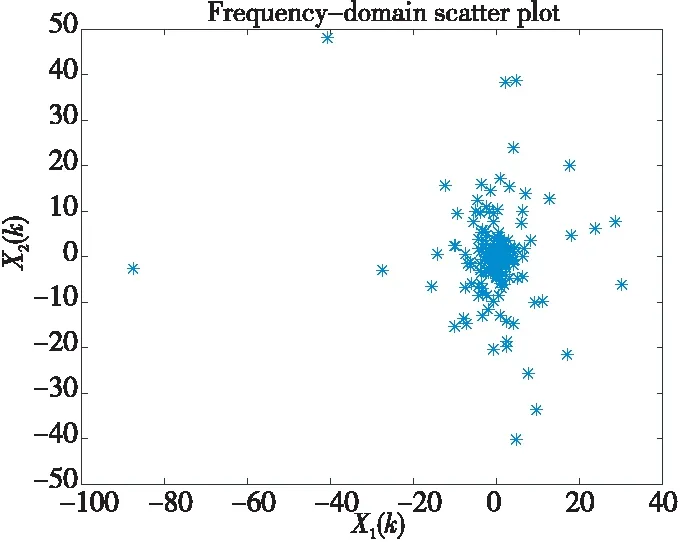
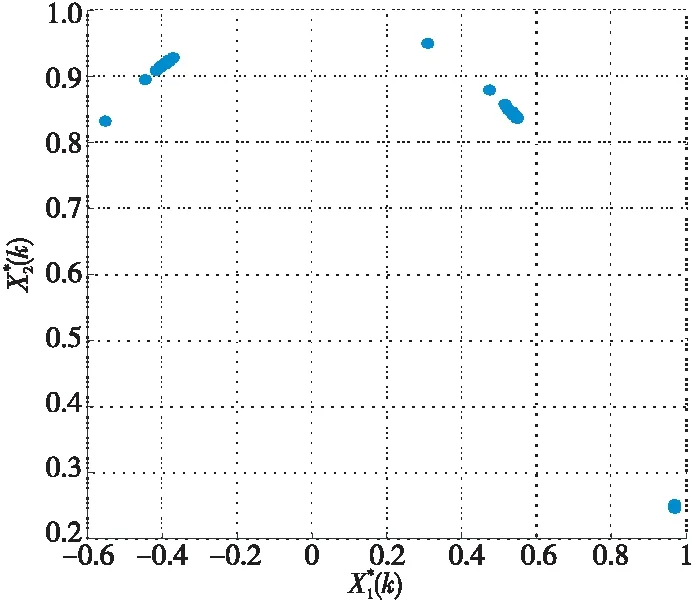
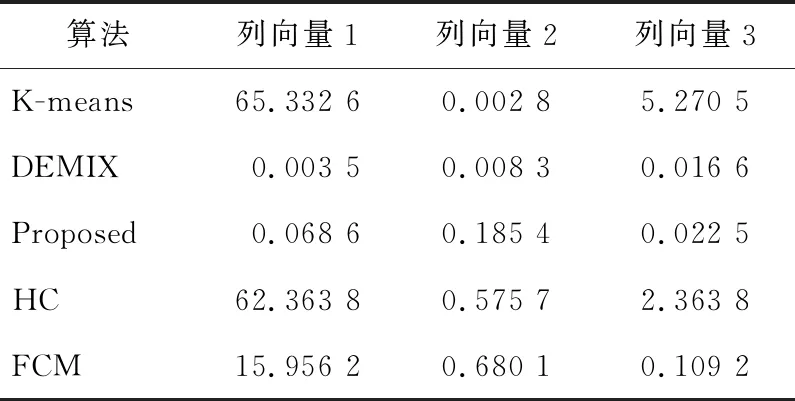
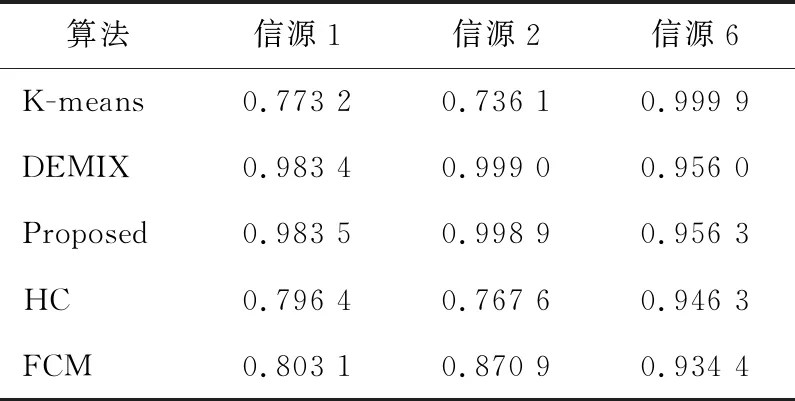
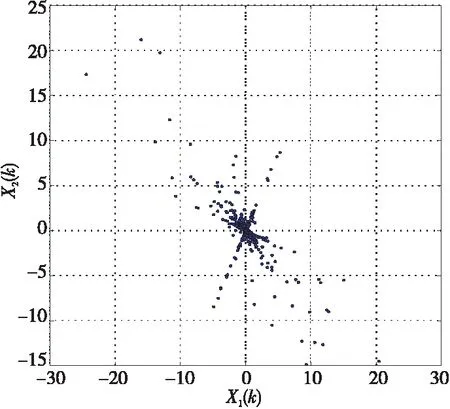
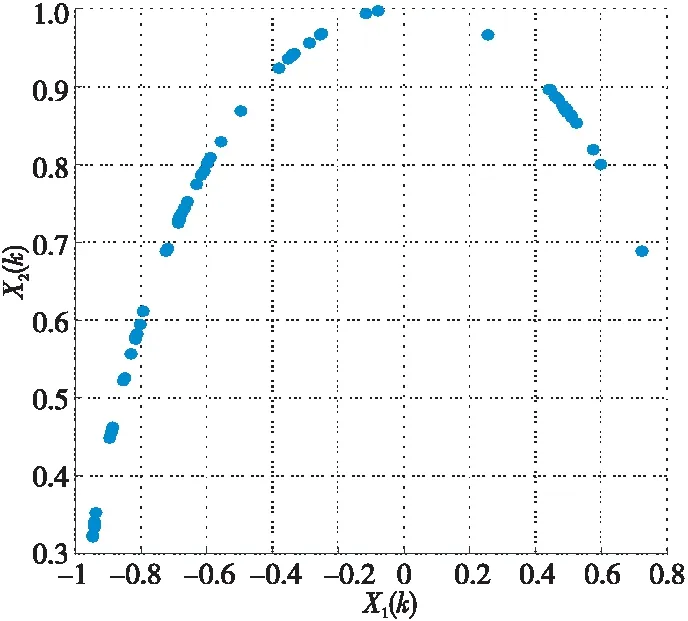
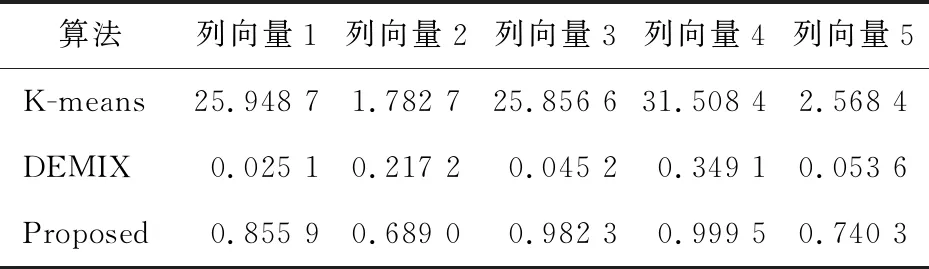
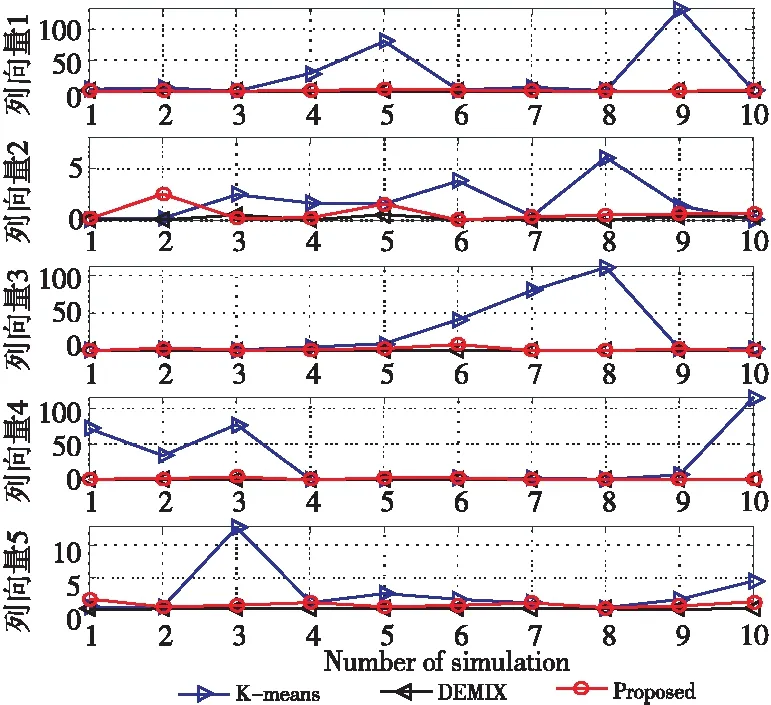
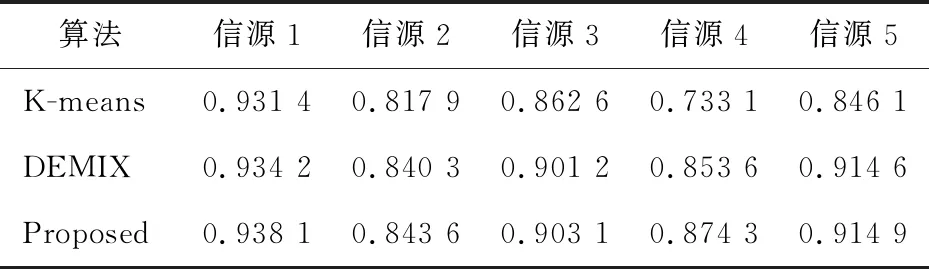
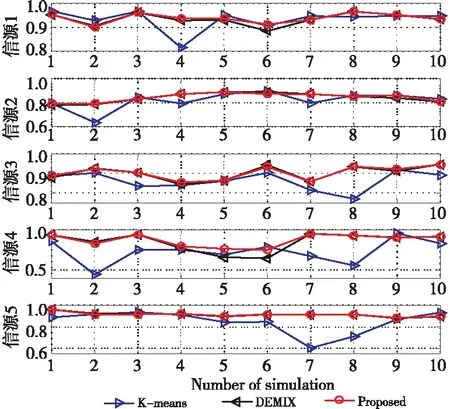
在无噪声情况下,盲信源分离BSS(Blind Source Separation)[1]的线性时域模型为x(t)=As(t),其中s(t)=[s1(t),s2(t),…,sm(t)]T是信源向量,x(t)=[x1(t),x2(t),…,xn(t)]T是观测信号向量,A∈Rn×m是体现传感器采集信道特性的混合矩阵。一般地,信源与传感器数量不相等,即m≠n。在BSS中,信源是不可观测的,即向量s(t)所包含的信源数未知,而传感器数量取决于信源的采集条件。在实际中,为节约成本,希望传感器数尽可能地少,这就出现了n 很多自然信号(如音频、图像和视频等)都是稀疏的。所谓稀疏信号是指非零元素很少,大部分元素都是零值的信号。实际应用中,充分利用信号本身稀疏性的方法是解决UBSS问题的首要方法[4]。对于充分稀疏的信号来说,它的数据分布具有线性聚类的特性[5]。因此,聚类方法就成为了分析稀疏信号的重要工具。常用的聚类方法有K-均值(K-means)[6]、霍夫(Hough)变换[7]和层次聚类(Hierarchical Clustering)[8]等,其中K-means在UBSS中应用广泛。然而,K-means具有2个明显的缺陷:(1)需要预先给定数据的聚类数量;(2)聚类结果对算法的随机初始划分非常敏感[9]。除了使用单独的聚类方法外,把2种不同的聚类算法进行组合,在估计欠定混合矩阵中也取得了很好的效果。例如,利用霍夫变换对K-means的聚类结果进行修正,从而提高欠定混合信道的估计精度[10];采取具有噪声的基于密度空间聚类DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法[11]确定数据的聚类数量和聚类中心,再利用Hough变换对DBSCAN的结果进行修正[12],实现了对欠定系统混合矩阵的有效估计;在DBSCAN聚类形成密度基数据的基础上,采用快速搜索与寻找密度峰值聚类CFSFDP(Clustering by Fast Search and Find of Density Peaks)[13]进一步计算出对应的密度峰值,以解决欠定混合矩阵的估计问题[14]。 正是基于组合聚类的思想,为充分体现信号的稀疏性,本文提出在频域中估计UBSS混合矩阵的分析方法。首先,利用傅里叶变换将时域中的观测信号转变成频域中的稀疏信号,并通过数据的归一化将稀疏信号的线性聚类转变成致密聚类;然后,利用相似性(姻亲)传播AP(Affinity Propagation)聚类[15]搜索观测数据的聚类数量和对应的聚类中心,并把AP聚类的结果作为K-means算法的初始参数,进一步修正数据的聚类中心,以提高欠定混合矩阵的估计精度;最后,利用线性规划(最短路径)法恢复信源。 本文其它部分组织如下:第2节介绍观测信号的预处理,包括傅里叶变换以及数据的归一化;第3节致力于稀疏信号的聚类分析,利用AP聚类实现对信源数目的自动搜索,并采用K-means进一步估计欠定混合矩阵的各个列向量;第4节介绍利用最短路径法分离信源;第5节采用音频信号进行仿真,以验证算法有效性;第6节为结束语。 在时域线性UBSS模型x(t)=As(t)中,混合矩阵A的元素aij(1≤i≤n,1≤j≤m)为常数,将A分解为列向量: A=[a1,a2,…,am] (1) 其中ai=[a1i,a2i,…,ani]T,i=1,2,…,m。则UBSS模型又可以表示为: x(t)=a1s1(t)+a2s2(t)+…+amsm(t) (2) 一般地,信号在时域中的稀疏性体现得并不充分[5],因此通常在频域中对信号进行聚类分析。对模型x(t)=As(t),在2边分别进行短时傅里叶变换STFT(Short Time Fourier Transform): (3) 其中,X(k)=[X1(k),X2(k),…,Xn(k)]T和S(k)=[S1(k),S2(k),…,Sm(k)]T分别为x(t)∈Rn和s(t)∈Rm的STFT系数向量,变量k是频率抽样点,而ai是矩阵A的第i个列向量。假设信源S(k)中所有信号都是完全稀疏的,即对于任一个频域的样本点k,仅有一个信源Si(k) (i=1,2,…,m)是非零值,其余信源Sj(k) (j≠i)均为零值,即: X(k)=aiSi(k),i=1,2,…,m (4) 或者 (5) 式(5)给出的是直线方程,且每个信源对应于一条直线,其方向向量ai=[a1i,a2i,…,ani]T就是混合矩阵A的第i个列向量。对完全稀疏的信号,其数据具有线性聚类(Linear Clustering)的特性。在UBSS模型中,可以把对混合矩阵的估计转变成对聚类形成的数据直线方向向量的估计。 实际上,信号的稀疏性在频域中并未得到充分体现。即在每个离散频率点k上,可能会有2个或2个以上信号具有非零值,使得信号的数据点不能形成理想的直线聚类特性。故采用单源点SSP(Single-Source-Point)检测[14,16,17]增强稀疏信号的线性聚类特性。 一般地,一条直线的方向可以由2个方向向量来描述。例如,在三维空间中,一条经过原点的直线可以由方向向量(1,1,1)和另一个方向向量(-1,-1,-1)来描述。为了把一条直线用唯一的方向向量来描述,可以采用一种称为镜像映射(Mirroring Mapping)[4]的方式,将负方向的向量(-1,-1,-1)映射到对应正方向的向量(1,1,1)上,即把平面或空间上的一条直线映射成对应的正方向上的一条射线。在信号处理领域,上述镜像映射的过程实际上就是对信号归一化。频域中归一化的观测信号为: (6) 其中,X(k)表示频谱值,‖·‖表示欧几里得(Euclidean)范数。显然,观测数据的归一化是把负频率方向的数据点映射到对应正频率方向的数据点上,形成了在上(正)半个单位圆(或单位球)上密集的数据堆。每一条聚类形成的数据直线都被映射成在上半个单位圆(球)上唯一的一堆数据。即镜像映射是把稀疏信号的线性聚类转变成观测数据在正方向单位圆(球)上的致密聚类(Compact Clustering)[4]。 通过观测数据归一化,对欠定混合矩阵的估计就转变成频域中对上半个单位圆(球)观测数据的聚类分析。由致密聚类特性[9],在每一个密集的数据堆中,都存在一个关键的数据(聚类中心),该数据的方向就对应于线性聚类的直线方向。因此,通过搜索每一堆数据的聚类中心,就可以估计欠定混合矩阵的列向量。 聚类分析能够将具有一定特质的数据划分为一族,而属于不同族的数据则易于区分。平方误差和准则(Sum-of-Squared-Error Criterion)是聚类分析中使用最广泛的准则函数,利用该准则能够对致密数据集进行很好的分类[9]。 在众多聚类算法中,K-means采用平方误差和准则,以迭代优化步骤搜索数据最优划分[9]。由于它易于实现,被认为是经典的聚类分析法,特别是对于密集数据堆和球(超球)的数据分布形状,K-means能获得理想的聚类效果[18]。尽管如此,K-means的弱点同样也很明显:使用算法的前提是要给定数据的聚类数量;聚类效果对算法随机产生的初始划分非常敏感,即要求有一个合理的初始化。显然,UBSS无法满足这2个要求。因此,本文采用AP聚类作为K-means的输入参数,以弥补K-means需要人为干预的缺陷,从而提高欠定混合矩阵的估计精度。 基于相似性(Similarity)测度的数据聚类在数据分析和工程系统中具有重要的作用[15]。一种常见的方法是使用数据来学习一组(聚类)中心,使得数据点与其最近的中心之间的平方误差和最小。当聚类中心是从实际的数据点获得,则称其为范例(Exemplars)[15]。AP聚类最明显的优势是将所有的数据点都等同地考虑为潜在的范例[15],这样就有效地避免了随机选择初始聚类中心的局限性。 对于数据点xi和xk,定义它们之间的相似性测度为: sim(i,k)=-‖xi-xk‖2 (7) 为了寻找合适的范例,AP聚类在搜索过程中不断积累2个证据:责任性(Responsibility)和可用性(Availability)。责任性r(i,k)表示从点xi的角度来看,点xk作为点xi的范例的适合程度;而可用性av(i,k)则表示从候选样本点xk的角度来看,点xi选择点xk作为它的范例的适合程度。显然,r(:,k)+av(:,k)的数值越大,数据点xk作为最终聚类中心的概率就越大。根据不断累计的证据,AP通过一个迭代过程搜寻数据的聚类,直到高质量的范例(聚类中心)出现。证据信息r(i,k)和av(i,k)在AP聚类过程中可以被看作是对数概率比(Log-probability Ratios)。 当AP迭代开始时,将av(i,k)值初始化为零:av(i,k)=0;而责任性r(i,k)的计算规则如式(8)所示: (8) 在第1次迭代中,由于可用性av(i,k)=0,责任性r(i,k)为sim(i,k)和xi与其它候选范例之间相似性最大值的差。而在以后的迭代过程中,当一些数据点被有效地分配给其它的候选范例时,根据式(9)的更新规则,它们的可用性值av(:,:)将降到零以下(即为负值)。负的可用性数值将降低式(8)中一些相似性的有效值,从而在竞争中消除相应的候选范例。对k=i的情况,自责任性r(k,k)设置为点xk作为范例的偏好值减去点xi与其它候选范例之间相似性中的最大值,它反映了点xk作为一个范例的证据积累,用于纠正不合适分配造成的错误。 责任性r(i,k)更新规则(式(8))是让所有候选范例都争夺数据点的所属权,而式(9)所示的可用性av(i,k)更新规则是从数据点收集证据,用于说明每个候选范例是否会成为一个好的范例: av(i,k)=min{0,r(k,k)+ (9) 即av(i,k)设置为自责任性r(k,k)加上候选范例xk从其它点获得的正值的责任性之和。只有所得责任性的正值部分才被加到一起,这是因为对一个好的范例,必须(用正的责任性)解释它如何适合一些数据点,而不必(用负的责任性)解释它如何不适合一些数据点。当以xk为范例的其它点具有正值的责任性,而自责任性r(k,k)是负值时,点xk作为一个范例的可用性得到增强。为限制强的正值责任性的影响,式(9)中的总和被设置了阈值,即av(i,k)不能大于零。自可用性av(k,k)的更新规则为: (10) 基于其它点发送给候选范例xk正值的责任性,式(10)反映了点xk作为一个范例的累计证据。 在AP聚类中还有2个重要的参数:相似性矩阵Sim={sim(i,k)}对角元素构成的偏好p(k)=sim(k,k)以及抑制算法陷入振荡的阻尼因子λ。由式(8)可得自责任性的表示式如式(11)所示: 根据地域特点与现有资源,打造品牌概念,为游客提供具有本地特色的独创性商品服务,提高乡村的吸引力和影响力,让身处繁杂都市的游客从自发寻找心灵休憩之所,变成慕名前来游玩度假。此外,还应提升乡村旅游的文化价值,保护旅游重点区的“乡村性”,使其免于在城市化进程中丢失自身的民俗文化。 (11) 由式(9)和式(11)可知,p(k)越大,则r(k,k)和av(i,k)就越大,点xk作为最终聚类中心的概率就越大。p(k)值将影响到哪个以及多少个范例将在竞争中胜出,最终成为聚类中心。这意味着,调整p(k)的值,可以增加或减少聚类数量。在实际应用中,一个较好的选择方案是将所有的p(k)值都设置为所有对应的数据点之间的相似性数值的中值(Median)。 当更新r(i,k)和av(i,k)的信息时,为避免出现数值振荡(Numerical Oscillations),对它们的迭代过程还需要利用阻尼因子进行抑制。在每一个迭代步骤i中,r(i,k)和av(i,k)的值要与最近一次迭代(步骤i-1)中的值r(i-1,k)和av(i-1,k)一起进行更新。考虑阻尼因子λ的迭代规则为: av(i,k)=(1-λ)av(i,k)+λav(i-1,k) r(i,k)=(1-λ)r(i,k)+λr(i-1,k) (12) 其中λ∈[0,1],其默认值为0.5。λ还可以改进算法的收敛性能。当由于振荡(或识别出的范例处于周期变化中)使得AP聚类无法收敛时,通过增加λ的值可消除振荡。 AP更新规则仅需要执行简单的局部计算,即只需在一对已知相似性测度的点之间交换信息。在AP过程的任何点(迭代步骤i),用av(i,k)和r(i,k)的组合即可识别出范例。对于点xi,找到使av(i,k)+r(i,k)最大化的点xk的值,当k=i时辨识出点xi作为范例,k≠i时,辨识出点xk是点xi的范例。即AP聚类总能找出数据的聚类数量和对应的聚类中心。显然,把AP聚类的结果作为K-means初始条件,不仅克服了K-means的缺陷,同时还保持了经典K-means的优势。 在获得混合矩阵估计之后,“两步法”的第2步是分离信源。考虑到环境噪声,UBSS的时域模型为x(t)=As(t)+v(t),其中v(t)∈Rn是加性高斯噪声向量。对于充分稀疏的信源,其观测信号在频域中每个离散的频点上,仅有一个分量具有非零值,其余分量均为零值,即给定的非零分量为稀疏分布。所谓稀疏分布是指在自变量为零时有尖峰,且随着自变量增大尖峰拖了一个很长的尾部,例如双边指数(拉普拉斯)分布。稀疏性等价于非高斯性。 对于稀疏信号,频域中的盲源分离则是通过如式(13)所示的优化问题[3]实现的: (13) 其中,σ2是噪声的方差。式(13)的第1项为均方重建误差的和(高斯噪声的对数似然性),而第2项为对非稀疏性(假设独立的拉普拉斯信源或超高斯信源)的处罚。 式(13)是个多变量优化问题,它需要同时估计混合矩阵A和信源S。由于利用组合聚类方法(见第3节)已经估计出混合矩阵A,因此,优化问题(13)简化成式(14)所示的形式: (14) 在BSS问题中,含噪声BSS(Noisy-BSS)和UBSS模型都是BSS的难点[2]。一般地,BSS模型仅考虑无噪情况(in the absence of noise)[3,4,12],因此,式(14)的优化问题可进一步简化为式(15)[3]: k=1,2,…,F (15) 其中F为离散频率范围。式(15)是只有1个变量的优化问题,即线性规划问题,求解较容易。 为验证本文算法的有效性,考虑在恶劣环境中仅用2个传感器采集多信源进行仿真。仿真中,对本文算法(Proposed)、K-means算法[6,19]、层次聚类HC(Hierarchical Clustering)算法[8,20]、模糊C均值FCM(Fuzzy C-means)算法[21]、混合矩阵方向估计DEMIX(Direction Estimation of MIXing matrix)算法[22]的性能进行比较。为得到公平的结果,各算法仿真环境都完全一样。 仿真的PC机配置为:Intel(R) Celeron(R) 1007U-1.5 GHz的CPU,4 GB内存,操作系统为Windows 10,所有仿真都在Matlab 9 (R2016a)上运行。测试的音频信源为SixFlutes (长笛演奏音乐)数据集[3],信源向量为s(t)=[s1(t),s2(t),s3(t),s4(t),s5(t),s6(t)]T,信号采样率为44.1 kHz,每个信号长度为216=65536个样本。每次仿真从s(t)中随机抽取不同数量和不同位置的信号。 为了度量各算法对混合矩阵的估计精度,采用如式(16)所示的角度偏差(Angular Deviation)[5]指标进行度量: (16) 其中,a是原始混合矩阵A的某个列向量,b是估计的混合矩阵B对应的列向量,而〈a,b〉表示向量a与b的内积。角度偏差d(a,b)的值越小,说明混合矩阵的估计精度越高。 在获得混合矩阵的估计之后,利用最短路径法[3]即可分离出信源。为度量原始信源与估计的信源之间的相似性,采用如式(17)所示的相关系数(Correlative Coefficients)[14]指标进行度量: (17) 其中,si(t)是时域中第i个信源,rj(t)是时域中第j个被分离的信源,T是时域中信号的样本数。若分离的信源与原始信源越相似,其相关系数ρii的绝对值就越接近于1,而ρij(i≠j)越接近于0。 首先,在时域中进行信号混合。利用Matlab随机地产生混合矩阵A,把音频信源s(t)转变成观测信号x(t)=As(t)。 对于时域中的观测信号x(t),利用Hanning窗截断来实现音频信号分帧。一般地,需要将一个完整信号分成整数帧,帧的数量取2的整数次幂,本文取23=8。由于每个信号的长度为65 536,可得每个音频帧长为L=65536/8=8192。为避免音频信号所含信息的损失,要求连续(相邻)2帧之间的样本要重叠。实际中,连续2个音频帧之间重叠样本数为d=round(0.15×L×4),其中round(x)为对x取整。于是可得到d=4915,即连续2帧的重叠率为60%。 然后,在频域中估计混合矩阵。利用STFT对时域信号x(t)的每一帧(采用同样的Hanning窗)进行变换,并且只取正频率范围内频谱(实部与虚部)的L个STFT系数,将连续(相邻)的频域帧衔接起来就形成一个信号,从而获得频域信号向量X(k)。为便于聚类分析,对X(k)进行镜像映射获得归一化的数据X*(k)。 对于归一化信号X*(k),本文算法首先利用AP聚类自动搜索聚类数量和对应的聚类中心,然后把该结果作为K-means的输入参数,实现对聚类中心(矩阵列向量)的精确估计。 最后,在得到混合矩阵估计之后,利用线性规划方法分离频域的信源。对每个分离出的频域信源,STFT的系数向量被分解成帧,其实部和虚部分量又被重新组合成复系数,频谱也拓展到负频率范围;对该频谱利用逆STFT(使用同样的Hanning窗)再变换到时域中。将时域信号每一帧乘以对应的逆Hanning窗,在连续2帧重叠部分的2边各移除50%的样本,仅保留帧的中间部分,把这些时域帧按先后顺序衔接起来,得到分离的信源,并计算相关系数。 5.3.1 2个传感器采集3个信源 由Matlab命令randi([1,6],1,3)随机抽取3个信源s(t)=[s1(t),s2(t),s6(t)]T,由命令A=2*rand(2,3)-1随机地生成代表白噪声信道的矩阵为A2×3=[-0.0798,0.3703,0.1458; 0.8008,-0.1234,0.9501],由x(t)=As(t)=[x1(t),x2(t)]T得到时域观测信号,其时域散点图如图1所示。 从图1知,时域中的数据点在坐标原点附近形成密集的数据族,没有体现信号的稀疏性,无法进行聚类分析。为此,将时域观测信号x(t)利用STFT变换成频域信号X(k)=[X1(k),X2(k)]T。频域中信号X(k)的散点图如图2所示。 Figure 1 Time-domain scatter plot of the observed signals图1 观测信号的时域散点图 从图2可看出,虽然频域中观测信号X(k)的稀疏性得到了一定的体现,隐约有数据点形成直线,但线性聚类并不明显。还需要对频域信号采用单源点SSP检测[14,16]技术进行预处理,以提高信号的线性聚类特性。 Figure 2 Frequency-domain scatter plot of the signals图2 观测信号频域散点图 在频域中,SSP是指仅有一个信源具有较大能量而其余信源能量很小以致可被忽略的频率点。然而在很多频点上,2个或2个以上信源都具有较大的能量值,这些频点就称为多源点MSP(Multi-Source Point)。正是MSP影响了信号的线性聚类。SSP检测就是利用信号频谱实部与虚部夹角的余弦[14,16]作为相似性度量,通过合适的阈值,检测并删除MSP,从而体现由SSP数据点形成的线性聚类特性。经过SSP检测后信号X(k)的散点图如图3所示。 Figure 3 Frequency-domain scatter plot after SSP图3 SSP检测后的频域散点图 从图3可看出,经过SSP检测,观测数据在频域散点图上形成了明确的3条直线,即直观地给出了不可观察的信源数量;欠定混合矩阵的列向量则体现为数据直线的方向向量。然而,基于平方误差和准则的聚类方法都是把观测数据划分为不同形状和不同大小的数据族,这就需要用镜像映射将线性聚类转变成致密聚类,形成在正半个单位圆上数据的密集聚类。经过归一化后的数据散点图如图4所示。 Figure 4 Normalized scatter plot of the signals图4 信号的归一化散点图 从图4可以看出,在正的半个单位圆上,归一化数据形成密集的数据堆,而堆的数量就是线性聚类形成的直线数量(信源数量)。另外,图4中数据并没有被完全聚到一起,还有部分数据需要进一步归类到对应数据堆中,这正是各种聚类方法所要执行的聚类任务。 对于归一化的数据,分别采用5种聚类算法搜索聚类的数量和相应的聚类中心,从而估计欠定混合矩阵。各方法的参数设置如下:在本文算法中,当AP聚类的阻尼系数取默认值λ=0.5时,形成的聚类中心数值周而复始地重复振荡,为此本文取λ=0.9消除其周期性。DEMIX算法采用观测数据对混合矩阵列向量进行计数和方向估计。K-means算法的初始聚类中心采用欧氏距离算术平均值法[19],聚类重复次数为1,最大迭代次数为100,算法的停止规则是相邻2次聚类中心的迭代值相同。HC算法采用文献[20]中的“Algorithm 1”,该算法已给出了R代码,仿真中将R改写成Matlab命令执行。FCM采用文献[21]中的“Algorithm 2”,其中范数为欧氏距离,指定聚类数量C,以样本点到聚类中心隶属度大小划分数据归类。 基于生成的混合矩阵A2×3,5种算法估计得到的混合矩阵分别为: A1=[-0.9457,0.9487,0.0598; 0.3252,-0.3162,0.9908] A2=[-0.0991,0.9487,0.1514; 0.9951,-0.3163,0.9885] A3=[-0.1003,0.9477,0.1513; 0.9949,-0.3192,0.9885] A4=[-0.9288,0.9520,0.0532; 0.3361,-0.3151,0.9911] A5=[-0.9459,0.9491,0.0601; 0.3308,-0.3149,0.9881] 其中A1,A2,…,A5分别表示K-means、DEMIX、Proposed、HC和FCM算法估计的矩阵。 由此可得5种算法在估计混合矩阵各个列向量时,所引起的角度偏差值如表1所示。 Table 1 Angular deviation of 3 sources separatedfrom 2 observed signals 由表1可以看出,DEMIX算法的性能是最优的,这是由于DEMIX是为估计混合矩阵列向量方向而专门设计的算法[22],它的角度偏差指标本就应该是最好;其它几种都是通用聚类算法,只是将它们用于估计混合矩阵。K-means对第2个列向量估计的角度偏差值是这5种算法中最小的,说明K-means确实是经典的聚类算法,然而K-means、HC、FCM 3种算法对其它列向量估计的角度偏差却很大,尤其是K-means和HC算法对第1个列向量估计的角度偏差都超过62。尽管本文算法对混合矩阵各列向量估计的角度偏差指标不是5种算法中最优的,但也仅次于DEMIX的结果,并且其值都小于0.2,明显优于其它3种聚类算法。 利用各种算法估计出的混合矩阵B,采取最短路径法在频域分离信源,通过逆STFT转换成时域信号,从而计算出原始信源与估计信源之间的相关系数,其结果如表2所示。 Table 2 Correlative coefficients of 3 sources separatedfrom 2 observed signals 从表2可以看出,对于恢复信源与原始信源的相似性指标,本文算法与DEMIX算法的估计性能几乎是相同的。尽管K-means对信源6的分离性能是这5种算法中最优的,但它与HC、FCM对其它信源的分离效果较差。 对照表1和表2的结果可知,混合矩阵列向量的角度偏差指标与分离信源的相似性指标并不完全一致。这是因为混合矩阵是在频域中估计的,而信源的相关系数是在时域中计算的。从仿真过程可知,频域信源正频率的STFT系数向量采用Hanning窗分帧,相邻2帧的样本要重叠,将STFT实部和虚部重新组合成复系数且把频谱拓展到负频率的范围;然后再利用相同长度的Hanning窗对该频谱进行逆STFT变换到时域中;采用时域Hanning窗进行分帧,并在相邻2帧重叠部分的2边各移除50%的样本,仅保留帧中间部分,从而构成时域信源。显然在STFT和逆STFT过程中的数据分帧、样本重叠、样本移除操作,会造成部分样本发生变化,使得2种指标产生不一致现象。 为了比较5种算法对混合矩阵估计和信源分离的总体性能,对以上仿真过程重复进行了10次,每次分别记录各算法对混合矩阵各列向量估计的角度偏差值,其结果如图5所示。同时,记录各算法对各个分离出信源与原始信源的相似性指标,其结果如图6所示。 Figure 5 Angular deviation of 3 sources separated from 2 observed signals图5 由2路观测信号分离3路信源的角度偏差 从图5可看出,在10次仿真中,DEMIX算法与本文算法的角度偏差值基本保持一致,都是小于1的,即这2种算法对混合矩阵的估计性能是优秀的。而K-means角度偏差最大值竟达到149.881 9,HC的最大角度偏差值为66,FCM的最大角度偏差值为22.421 7,说明这3种算法对欠定混合矩阵的估计性能较差。 Figure 6 Correlative coefficients of 3 sources separated from 2 observed signals图6 由2路观测信号分离3路信源的相关系数 从图6及记录的数据可知,本文算法在10次仿真中最小的相关系数为0.956 3,DEMIX的最小相关系数为0.952 2,这2种算法的绝大多数相关系数都在0.99以上,说明它们具有很好的UBSS性能。而K-means在10次仿真中最小相关系数为0.493 0,HC最小相关系数为0.499 3,FCM最小相关系数为0.559 9,这3种算法大约有一半的相关系数小于0.9,说明这3种算法恢复的信源相对于原始信源产生了较大失真。 由以上的仿真结果可知,DEMIX与本文算法在估计混合矩阵和分离信源方面的性能大致相同。其它3种算法的性能属于同一级别,并且K-means是这3种算法中性能最差的。因此,在下面的仿真中,只对DEMIX、K-means和本文算法的性能进行比较。 5.3.2 2个传感器采集5个信源 5个信源s(t)=[s1(t),s2(t),s3(t),s4(t),s5(t)]T,由Matlab命令A=2*rand(2,5)-1随机生成混合矩阵为A2×5=[0.8394,-0.7207,0.1236,-0.9114,0.3763;-0.5956,0.7679,-0.3332,0.3283,-0.6618],时域观测信号为x(t)=As(t)=[x1(t),x2(t)]T。然后,x(t)通过STFT变换成频域信号X(k)=[X1(k),X2(k)]T,频谱X(k)的散点图如图7所示。归一化数据X*(k)的散点图如图8所示。 Figure 7 Frequency-domain scatter plot of 5 sources and 2 observed signals图7 2路观测信号(5信源)的频域散点图 Figure 8 Normalized frequency-domain scatter plot图8 2路观测信号(5信源)的归一化散点图 对于图8的归一化观测数据,利用DEMIX、K-means和本文算法分别对混合矩阵各列向量进行估计。这3种算法的参数设置如前所述,而且仿真过程与上一个仿真类似。 为了全面地比较这3种算法对混合矩阵的估计性能,同样的仿真过程重复进行10次,计算并记录10次仿真中混合矩阵列向量估计的平均角度偏差值,其结果如表3所示。 Table 3 Average angular deviation of 5 sources separated from 2 observed signals 从表3可知,DEMIX和本文算法的平均角度偏差值都小于1,但DEMIX要优于本文算法。而K-means的平均角度偏差值都大于1,且有3个列向量的平均角度偏差值都在25以上。 为了更直观地观察每次仿真中各算法估计混合矩阵列向量的角度偏差值的变化情况,图9给出了10次仿真的结果。 从图9及记录的数据可知,DEMIX的最大角度偏差值为1.163 3,本文算法的最大偏差值为2.547 1;K-means的最大偏差值为132.428 6。显然,K-means估计混合矩阵的误差较大。 同样地,在10次仿真中,3种算法分离5个信源的平均相关系数值如表4所示。 从表4可知,DEMIX和本文算法恢复信源的平均相关系数几乎是相同的,而且只有2个信号的相关系数小于0.9。而K-means对4个信号的平均相关系数都小于0.9,其中最小的相关系数仅有0.733 1。 Figure 9 Angular deviation of separating 5 sources from 2 observed signals图9 2路观测信号(5信源)的角度偏差 算法信源1信源2信源3信源4信源5K-means0.931 40.817 90.862 60.733 10.846 1DEMIX0.934 20.840 30.901 20.853 60.914 6Proposed0.938 10.843 60.903 10.874 30.914 9 图10给出了3种算法在每次仿真中恢复信源与原始信源相关系数的变化波形。 Figure 10 Correlative coefficients of 5 sources separated from 2 observed signals图10 由2路观测信号分离5路信源的相关系数 从记录的数据可知,在5个信号的10次仿真中,本文算法的相关系数最小值为0.754 1,最大值为0.964 5;DEMIX的最小值为0.650 7,最大值为0.965 4;K-means的最小值为0.445 3,最大值为0.967 1。从图10的相关系数波形也可以看出,DEMIX与本文算法分离信源的相似性指标基本一致,而K-means的相关系数值波动较大,说明它对信源分离的性能不稳定,产生了较大的分离误差。 综合考虑以上2个仿真,可以得出如下结论:(1)在固定传感器数量(2个)的情况下,随着信源数目的增加,各种聚类算法对混合矩阵的估计性能以及对信源的分离性能都会下降。这是由于在UBSS系统中,信源之间会产生干扰,信源数量越多,采集传感器遭受的干扰就越强,因而造成算法对UBSS的估计性能下降。(2)由于DEMIX是专门用于估计混合矩阵列向量方向的算法,因此在角度偏差的指标上,它相对其它聚类算法具有一定的优势。尽管如此,本文算法仍能和DEMIX保持基本一致的(性能指标)水平。(3)单独的聚类算法,如K-means、HC和FCM,对混合矩阵估计和信源分离的效果都不理想,产生了较大的估计误差。基于此,本文将2种聚类算法相结合,首先利用AP聚类辨识出信源(类)数量和聚类中心,再利用K-means进行聚类中心(关键数据)的定位修正,从而提高混合矩阵以及信源的估计精度。 针对稀疏信源的UBSS问题,本文提出了在频域中估计混合矩阵的聚类分析算法。首先利用STFT将时域观测信号转变成频域中的稀疏信号,以增强信源的线性聚类特性。然后利用镜像映射将线性聚类转变成致密聚类,以实现对观测信号的归一化。在此基础上,利用聚类方法搜索数据族的数量和对应的关键数据。为了克服K-means算法本身的缺陷,本文利用基于相似性传播的AP聚类自动搜索出不可观测的信源数量和相对应的数据聚类中心,并将AP聚类得到的结果作为K-means的输入参数,对UBSS系统混合矩阵的列向量进行精确的估计。把AP和K-means相结合的优势,不仅可以提高对UBSS系统的估计精度,而且也弥补了K-means算法需要人为干预(即需要指定聚类数量以及对初始化敏感)的不足。2 观测数据的预处理
3 聚类分析法搜索关键数据
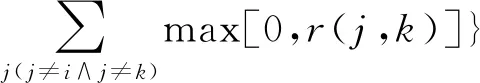
4 线性规划方法分离信源
5 仿真结果与分析
5.1 仿真环境与性能指标
5.2 仿真过程
5.3 仿真结果



6 结束语

