基于三维坐标修正的改进型3DDV-Hop定位算法 *
罗施章,张 晶,2,3,4,王健敏
(1.昆明理工大学信息工程与自动化学院,云南 昆明 650500;2.昆明理工大学云南省人工智能重点实验室,云南 昆明 650500;3.云南枭润科技服务有限公司,云南 昆明 650500;4.昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500;5.云南省农村科技服务中心,云南 昆明 650021)
1 引言
随着人类社会智能信息化时代的到来,无线传感器网络[1]在各个领域中的应用价值越来越突出,尤其是在工农业、环境保护、军事安全、社会安全等领域中的应用更为广泛。例如在对特定湖泊区域水下数据的监测过程中,结合无线传感器网络随机布置一定数量传感器节点在特定水下三维空间区域中,并对各节点处温度、湿度、压强、污染物密度等数据进行实时采集,对所采集数据进行后台实时分析遴选出数据异常节点,及时对三维空间区域中各异常节点位置处采取相应环境整治措施,以达到对生态环境进行保护的目的,而采取整治措施的前提是获取异常节点位置,若需获取各监测节点处坐标则需结合节点的定位算法[2]求解其坐标。
随着应用场景空间维度的提升,为降低算法计算复杂度以及对未知节点定位成本,目前将无需测距的传统3DDV-Hop (3D Distance Vector Hop)定位算法作为各应用场景中对节点定位的主流算法,而该算法由于对各节点间跳数、跳距计算不准确,从而影响了未知节点与各锚节点间距离计算,导致未知节点定位误差较大;为降低跳数、跳距计算误差,各类基于节点间跳数、跳距计算进行改进的定位算法被陆续提出。但是,这些改进定位算法对节点间跳数、跳距的计算方法有待优化,且未对所求得未知节点在三维空间中坐标位置进行修正以进一步降低未知节点定位误差[3]。
为解决上述问题,本文提出一种基于三维坐标修正的改进型3DDV-Hop定位算法。该算法首先通过为各锚节点设定3种不同的通信半径[4]进行数据信息广播,各节点根据不同通信距离记录最小跳数,从而降低各节点间最小跳数计算误差;然后结合该最小跳数分别构建各锚节点间跳数权值Wij(其中,i和j分别为第i个锚节点和第j个锚节点,i≤i,j≤S×V,S为节点总数,V为锚节点比例)、各未知节点与各锚节点间跳数权值Wki(其中,k和i分别为第k个未知节点和第i个锚节点,i≤k≤N,N为未知节点总数),根据各锚节点间跳数权值进行加权计算求得锚节点平均跳距值AVEHop;再根据该AVEHopi以及Wki加权计算出各未知节点AVEHopk值,通过该AVEHopk值以及未知节点与各锚节点间最小跳数MINHopki可计算得出未知节点与各锚节点间空间直线距离,并采用最大似然估计法求解得出各未知节点在三维空间中的估计坐标;最后对邻居锚节点数大于或等于2(邻居节点数决定了构建的空间正方体数量,当空间正方体数量大于或等于2时才可形成交叉区域)的未知节点依据各未知节点与各相邻锚节点间距离构建正方体交叉区域[5],并对未处于该交叉区域中的未知节点进行坐标修正,以进一步降低定位误差。
2 传统3DDV-Hop算法及改进算法
2.1 传统3DDV-Hop定位算法
2.1.1 算法原理
随着无线传感器网络的应用空间维度由二维平面拓展至三维空间,节点坐标计算复杂度及定位成本随之增加,传统DV-Hop算法需在原有基础上改进为传统3DDV-Hop定位算法,以适应空间维度提升的定位场景。传统3DDV-Hop算法定位步骤可简述如下:
首先由传感器网络中各节点向位于半径为R的球体范围内各相邻节点广播数据信息包(包含节点ID、节点跳数等信息),直至各节点间最小跳数均记录在路由向量信息表中(相邻节点间最小跳数为1);其次第i个锚节点可根据自身三维坐标(xi,yi,zi)以及与第j个节点间最小跳数MINHopij计算出自身平均跳距AVEHopi,如式(1)所示:
AVEHopi=
(1)
然后根据上述求得的AVEHopi和MINHopij可计算得知第k个未知节点与第i个锚节点间直线距离,如式(2)所示:
Dki=AVEHopi×MINHopki
(2)
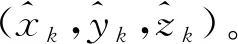
2.1.2 问题描述
(1)如图1所示,由于传统3DDV-Hop定位算法在计算节点A1与A4、A1与A5间最小跳数MINHopA1A4和MINHopA1A5时,是由各相邻节点间最小跳数累加而得,而各相邻节点间最小跳数均以1计,故通过计算可知,节点A1与A4、A1与A5间MINHopA1A4和MINHopA1A5值分别为2和1,但各相邻节点间实际直线距离差异较大,从而造成各节点间最小跳数计算误差较大。
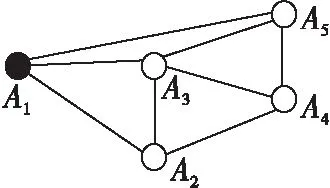
Figure 1 Schematic diagram of calculation error of minimum hop count图1 最小跳数计算误差示意图
(2)如图2所示,三维空间中a3与a1、a2、a4、a5间距离[6]相等,均为l,通过式(1)计算可知AVEHopa3为2l/3,结合该值与式(2)计算可知a3与a1、a2、a4、a5间直线距离Da3a1,Da3a2,Da3a4,Da3a5分别为4l/3,2l/3,2l/3,4l/3,从而造成通过传统3DDV-Hop定位算法所得各节点直线距离与实际距离差异较大。
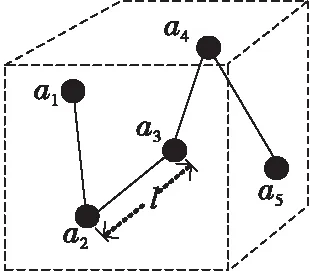
Figure 2 Schematic diagram of calculation error of average jump distance图2 平均跳距计算误差示意图
2.2 各类改进定位算法
2.2.1 算法原理
针对传统3DDV-Hop定位算法在计算未知节点坐标位置过程中存在的上述问题,文献[7]提出一种基于加权的3DDV-Hop定位算法[7],该算法通过构建跳数权值对锚节点平均跳距进行加权计算求解,从而降低未知节点定位误差;文献[8]提出一种基于跳数加权与跳距优化的3DDV-Hop定位算法[8],该算法通过对相邻节点间AVEHopij进行加权修正以及对AVEHopi结合最小均方误差进行优化计算,以此降低未知节点的定位误差。
2.2.2 问题分析
(1)传统3DDV-Hop定位算法虽然可求得未知节点在三维空间中坐标位置且计算简单,但是由于相邻节点最小跳数以及各锚节点平均跳距计算误差导致未知节点定位误差较大,实用价值不大。
(2)基于加权的3DDV-Hop定位算法虽通过构建跳数权值对各锚节点平均跳距进行了优化处理以降低未知节点定位误差,但是平均跳距计算过程中涉及各相邻节点间最小跳数,而最小跳数计算并未进行任何修正,各节点间最小跳数是直接通过对相邻节点间最小跳数进行累加所得,从而导致各锚节点平均跳距计算过程中所涉及的节点间最小跳数存在较大误差,以至于后续的平均跳距计算以及未知节点坐标计算存在较大误差。
(3)基于跳数加权与跳距优化的3DDV-Hop定位算法虽通过相邻节点间接收信号强度指示RSSI(Received Signal Strength Indication)值构建的跳数权值[9]以及最小均方误差降低了节点间最小跳数和各锚节点平均跳距的计算误差,但是在计算各相邻节点间最小跳数时只考虑通过外部优化方法对路由信息向量表中已记录各节点间最小跳数进行修正计算,并未从锚节点自身通信距离出发对MINHopij进行精确记录;且在AVEHopi计算过程中只针对AVEHopi进行优化计算并以此进行各未知节点与各锚节点间空间直线距离的计算,而并未同时结合未知节点平均跳距值进行优化计算,以进一步降低平均跳距计算误差。
上述各类改进算法最后均通过最大似然估计法[10]计算得出各未知节点估计坐标,并将该估计坐标值作为各未知节点最终坐标值,并未结合任何修正方法对其进行进一步求精。
针对上述问题,本文提出一种基于三维坐标修正的改进型3DDV-Hop定位算法。
3 本文所提改进型3DDV-Hop定位算法
3.1 设定不同通信半径记录最小跳数
首先为无线传感器网络中各锚节点设置3类通信半径,分别为R/3,2R/3,R;其次锚节点分别以3类通信半径向邻居节点广播数据信息包,当邻居节点处于2R/3通信半径球体范围内时,只需将相邻节点间MINHopij记录在路由信息向量表中即可,无需继续转发数据信息包;当邻居节点处于2R/3与R之间的环形球体范围内时,需将MINHopij记录在路由信息向量表的同时结合泛洪法[11]继续向自身邻居节点转发数据信息包。其中MINHopij具体记录法则如式(3)所示:
(3)
其中,DIS为相邻节点间空间直线距离,其值结合相邻节点间RSSI计算得出。RSSI具体计算如式(4)所示:
(4)
其中,Pr(d)、Pr(d0)分别为与参考节点相距d、d0处节点的RSSI值,可直接测得;而d0为标准参考距离,通常取d0=1 m;1≤η≤3为路径损耗指数;Xσ为高斯噪声。
如图3所示,当处于2R/3与R之间的环形球体范围内的邻居节点F接收到来自锚节点A的数据信息包时,将相邻节点间MINHopFA值记录在自身路由信息向量表中;并以同样方式(三通信半径)继续向位于通信半径范围外的邻居节点G转发数据信息包,节点G分别将MINHopAF、MINHopFG记录在路由信息向量表[12]中,并根据MINHopFG与三通信半径相对大小关系判定其是否继续转发数据信息包。
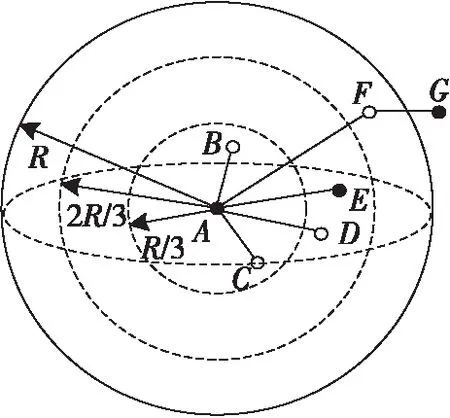
Figure 3 Schematic diagram of calculating the minimum hop count of three communication radii图3 三通信半径最小跳数计算示意图
各锚节点均根据上述通信方式进行泛洪广播,直至所有节点间MINHopij记录完毕。
3.2 加权计算平均跳距及未知节点坐标计算
通过上述三通信半径计算方法可知所有锚节点间最小跳数MINHopij,结合各锚节点在三维空间已知坐标(xi,yi,zi)、(xj,yj,zj),可计算出所有锚节点间平均跳距值AVEHopij,如式(5)所示:
AVEHopij=
(5)
与此同时构建所有锚节点间跳数权值Wij,根据该权值以及所有锚节点间AVEHopij通过加权计算得出所有锚节点AVEHopi,如式(6)所示:
AVEHopi=∑i≠jMINHopij×Wij
(6)
其中,
(7)
同理,通过第k个未知节点与所有锚节点间MINHopki构建权值Wki,如式(8)所示:
(8)
结合式(6)中AVEHopi以及式(8)中权值Wki,通过加权计算可求解出第k个未知节点平均跳距[13]AVEHopk,如式(9)所示:
AVEHopk=∑k≠iAVEHopi×Wki
(9)

(10)
对式(10)中各方程式间作差值运算,从而求解出未知节点估计坐标:X=(ATA)-1ATb,其中:
3.3 构建正方体交叉区域修正坐标
当未知节点邻居节点数大于或等于2时,通过RSSI[14]计算出未知节点与其相邻节点间距离,各邻居节点分别以自身为中心,以该距离值的2倍长度为边长构建空间正方体,若干正方体之间相互交错形成正方体交叉区域;若第k个节点未处在该正方体交叉空间中,则需结合如下规则对其三维坐标进行修正,如图4所示。
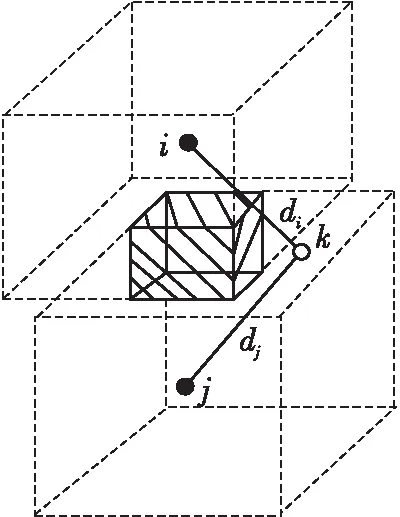
Figure 4 Schematic diagram of cube intersection area construction图4 正方体交叉区域构建示意图
设定图4中,第i个锚节点标为(xi,yi,zi),第k个节点(未知节点)与其距离为d,当未知节点未处于交叉区域中时,需对其坐标进行修正,具体修正规则如式(11)所示:
(11)
4 仿真实验及数据分析
4.1 评价指标及仿真环境
为充分对比各类算法对未知节点定位精确度,实验过程中将各类算法对所有未知节点(共N个)的平均定位误差值(ErrEvg)作为评价算法优劣的标准。结合节点在三维空间中实际坐标(xk,yk,zk),1≤k≤N,ErrEvg具体计算方法如式(12)所示:
ErrEvg=
(12)
算法采用Matlab 2016a版仿真软件,构建边长为100 m的湖泊水下三维空间区域仿真场景,如图5所示,设定节点总数(S)、锚节点比例(V)、节点通信半径(R)变化范围分别为300~1 000,15%~45%,30 m~100 m,各类实验条件下未知节点ErrEvg均由定位算法循环运行100次取平均值所得。
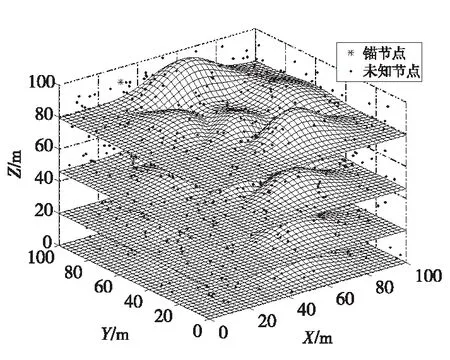
Figure 5 Distribution diagram of nodes in underwater three-dimensional space图5 水下三维空间节点分布图
4.2 实验结果对比分析
根据节点在三维空间的分布特点以及节点通信距离与空间范围的相对关系,首先在初始条件(R=60 m,S=1000)下,统计并对比分析传统3DDV-Hop定位算法(以下简称3DDV-Hop)、基于加权的3DDV-Hop定位算法(以下简称3DDV-Hop-WH)、基于跳数加权与跳距优化的3DDV-Hop定位算法(以下简称3DDV-Hop-HWHD)、基于三维坐标修正的改进型3DDV-Hop定位算法(以下简称3DDV-Hop-CDCR)共计4种算法的ErrEvg随锚节点比例(V)变化的情况,如图6所示。
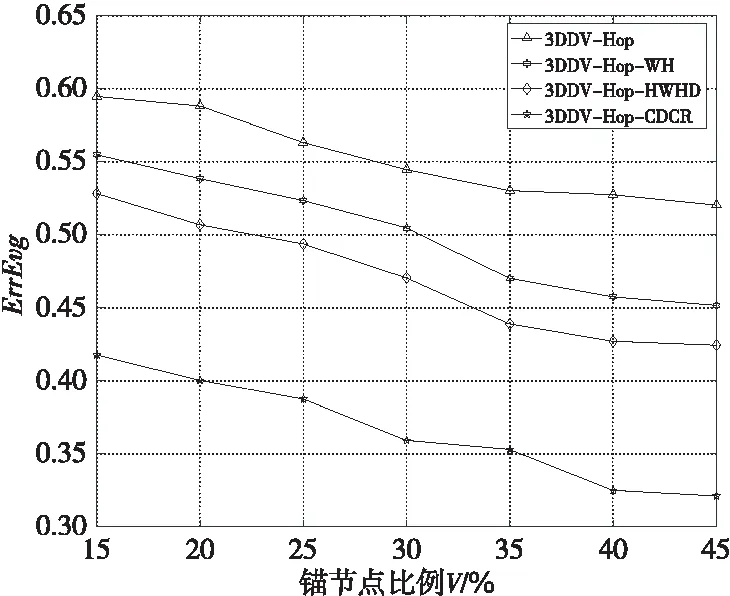
Figure 6 Broken line statistical diagram of ErrEvgchanging with anchor node proportion V图6 ErrEvg随锚节点比例V变化折线统计图
由图6统计结果分析可知,上述4种算法的ErrEvg随锚节点比例(V)的增加呈下降趋势,本文所提3DDV-Hop-CDCR算法相较前3种算法该值下降[0.0066,0.2737](区间下限由前3种算法的ErrEvg最小值与3DDV-Hop-CDCR算法ErrEvg最大值相减所得,区间上限由前3种算法的ErrEvg最大值与3DDV-Hop-CDCR算法ErrEvg最小值相减所得,后续ErrEvg下降区间求解方法相同)。
其次在初始条件(R=60 m,V=25%)下,统计并对比分析4种算法ErrEvg随节点总数(S)变化的情况,如图7所示。
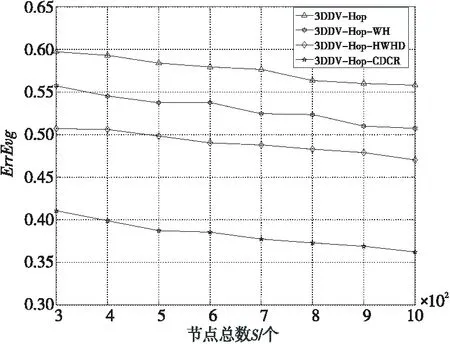
Figure 7 Broken line statistical diagram of ErrEvg changing with the total number of nodes S图7 ErrEvg随节点总数S变化折线统计图
根据图7统计结果分析可知,上述4种算法的ErrEvg随着节点总数(S)的增加,无明显变化趋势,且3DDV-Hop-CDCR定位算法相较前3种定位算法,其ErrEvg下降[0.0596,0.2350]。
最后在初始条件(S=1000,V=25%)下,统计并对比分析4种算法ErrEvg随节点通信半径(R)变化的情况,如图8所示。
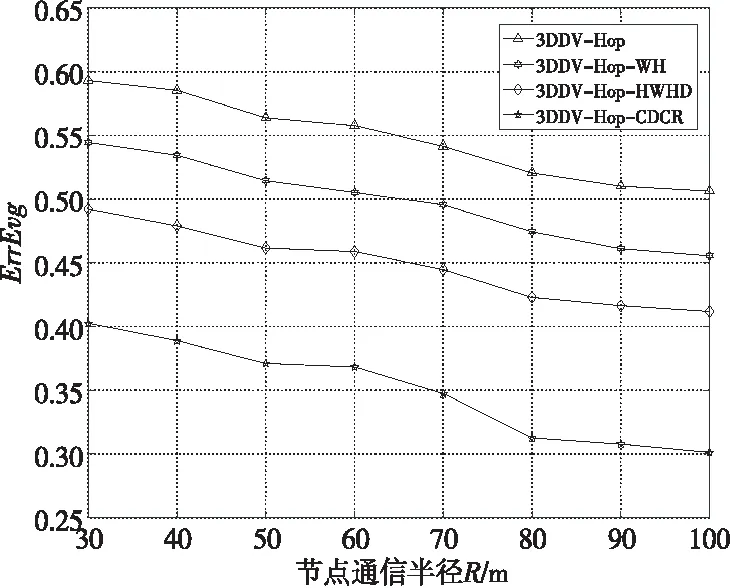
Figure 8 Broken line statistical diagram of ErrEvg changing with node communication radius R图8 ErrEvg随节点通信半径R变化折线统计图
根据图8实验统计结果可知,4种定位算法的ErrEvg随着节点通信半径(R)的增加呈现明显下降趋势,且本文3DDV-Hop-CDCR定位算法相较前3种定位算法,其ErrEvg下降[0.0093,0.2919]。
4.3 计算复杂度对比分析
本文所提3DDV-Hop-CDCR定位算法所涉及的问题规模大小与节点总数相关,而算法仿真过程中基本语句迭代次数由未知节点数N决定,故可令频度函数T(S)为:T(S)=(1-V)S,再将频度函数T(S)中所有未知变量全部换成未知因子ε,即T(ε)=ε-ε2,当ε趋近于无穷大时,存在函数f(ε)使得:
其中c为常数,从而得出f(ε)为T(ε)的同量级函数,故算法计算复杂度为O(ε2)。
而前述3种算法计算过程中,基本语句迭代次数也是由未知节点总数N决定,且本文所提算法相较前3种算法所投入锚节点比例并未有所下降,故4种算法未知节点总数相同,算法复杂度也相同,均为O(ε2)。
4.4 节点通信及部署代价对比分析
3DDV-Hop算法、3DDV-Hop-WH算法和本文3DDV-Hop-CDCR算法在定位过程中只涉及通过各锚节点间相互通信获取各锚节点间最小跳数,以计算各锚节点平均跳距,通信轮数为1。而3DDV-Hop-WH算法在定位过程需要各相邻节点间相互通信获取RSSI,以修正各相邻节点间最小跳数,以及各锚节点间相互通信获取节点间最小跳数,以求得各锚节点平均跳距,通信轮数为2,相较而言3DDV-Hop-WH算法节点通信代价较高。
由于4种算法所投入的锚节点比例相同,且锚节点数与所投放的GPS定位装置数对应,故4种算法的节点部署代价相同。
5 结束语
本文通过设定3类节点通信半径计算节点间最小跳数,以及通过加权运算降低各未知节点平均跳距,从而降低未知节点平均定位误差,并结合未知节点与邻居节点间直线距离构建正方体交叉区域,以修正未知节点坐标,进一步降低定位误差。实验结果表明,本文所提出的基于三维坐标修正的改进型3DDV-Hop定位算法,相较传统3DDV-Hop定位算法和各类改进的3DDV-Hop定位算法,其ErrEvg下降[0.0066,0.2919],显著降低,算法计算复杂度、节点通信和部署代价均未增加。

