Determination of the ground vibration attenuation law from a single blast: A particular case of trench blasting

Rfel Rodríguez, Lur Grcí de Mrin, Mrc Bscompt, Cristól Lomrdí,c

a Department of Mining Exploitation and Prospecting,School of Mining,Energy and Materials Engineering,University of Oviedo,Independencia 13,Oviedo,33004,Spain

b Department of Mining,Industrial and ICT Engineering,Polytechnic University of Catalonia(UPC),Manresa,Av.Bases de Manresa,61-73,Barcelona,08242,Spain

c Perforaciones Noroeste S.A, Longoria Carbajal No. 3, Oviedo, 33004, Spain

Keywords:Empirical analysis Blasting Ground vibration Trenching Wave propagation

ABSTRACT The general transmissivity law of ground vibrations was studied, and a user-friendly methodology for determining the behavior of vibrations generated in any rock mass is proposed.The study was based on a single blast in a trench excavation, analyzing the vibration components recorded from two fixed locations. The attenuation law and the main variables according to the legal requirements, frequency and peak particle velocity (PPV), are defined with this novel method, achieving a high confidence level in a simple manner. The proposed approach can also have an important impact in terms of reducing the potential consequences of vibrations for the surrounding construction and achieving the required definition of rock mass. Reducing the cost and time in many projects where blasting techniques are applied is particularly useful for the design of future blasts.

1. Introduction

The use of explosive charges is a widely adopted technique for rock mass breakage in mining and civil works due to its low direct and indirect costs(López-Jimeno et al.,2017).Therefore,it is crucial to properly define the main blasting features,such as the blasthole geometry, detonation scheme, and type of explosive, and to study the geotechnical characteristics of the rock mass that need to be broken (Kuzu, 2008).

On the other hand, many potential negative effects exist regarding the surrounding environment, the most important of which are flyrocks,seismic waves,and airblasts,and it is necessary to control them in order to comply with the existing laws and regulations. From those negative effects, seismic waves, which cause ground vibrations,might be the most dangerous and difficult to manage. Their impact is especially relevant when there is construction nearby (Tripathy et al., 2016). The limit values of ground vibration levels are usually established depending on the damage that the vibrations can cause and the type of construction,and this topic has been widely studied over time (Nicholls et al., 1971;Studer and Suesstrunk,1981; Konon,1985).

Vibrations can be defined as the transmission of the seismic wave in a blast that generates a movement of particles at each point.The initiation of the blast creates a pressure wave due to the explosive gases at high pressure and temperature. Initially, this wave has a cylindrical shape, which subsequently evolves to a spherical shape, creating deformation of the rock mass. The vibration wave is initiated in the elastic stage since pressure created during the blast is progressively reduced in the initial stages of the process (López-Jimeno et al., 2017). These waves are transmitted with very little energy consumption,mainly attenuated due to the increase in the volume affected by them. The stream of waves generated has a different frequency,mostly depending on the type of rock mass.The velocity of transmission is also dependent on the elastic rock mass characteristics and the presence of faults and fractures,producing a refraction and reflection of the wave.At short distances, the main influence of the blast is the explosive and geometric factors, while the geological characteristics and structures have much more influence at long distances (De Cospedal,2019).

The behavior of the waves through the rock mass is crucial for characterizing the vibrations (Aldas, 2010), especially when there are many different geological structures and variations. Each type of rock has a different response to vibrations,the higher the density,the higher the capacity to transmit vibrations(Blair and Armstrong,1999).

The influence of fracturing elements such as faults,cracking,and strata, among others, has been analyzed by many researchers (Ak and Konuk, 2008; Kuzu, 2008; Takahashi et al., 2018). The interaction of several layers and fracturing in the direction of the waves and their intensity were also analyzed by Shao et al. (2015) and Nateghi (2011). In addition, the level of vibration was studied and determined to be higher in the surface of the soil than in the contact between soil and bedrock (Wu et al.,1998). However, the velocity in soils is usually lower than that in rock because the elastic modulus is also lower(Jayasinghe et al.,2019).Several authors have also tried to correlate indicators such as the uniaxial compressive strength (UCS), geological strength index (GSI), and rock quality designation (RQD) with the level of vibrations (Ozer, 2008; Mesec et al., 2010; Kumar et al., 2016). The presence of water can also be an important element in the level of vibration, increasing in many cases studied (Singh and Narendrula, 2007).

When these vibrations reach any structure in their influence area, they can cause damage or, at a lower level, a certain discomfort to the residents, which can also lead to legal issues(Schexnayder and Ernzen, 1999). Therefore, it is necessary to consider the potential effect of blasting on the environment in the early stages of a project,especially when there are structures in the proximity (Yan et al., 2020), by considering the explosive charge,type of rock mass, and distance to the structure from the blasting.

The achievement of a transmissivity law for ground vibration is fundamental to predicting its behavior.One of the first publications regarding the ground vibration was the work of Rockwell (1927),studying the effect on structures. Further research has been conducted over time, making significant improvements to minimize the risk of blasting(Crandel,1949;Langefors and Kihlstrom,1978).

It is necessary to correlate explosive charge and distance to the building for each type of rock mass to control the vibration produced. This information is very useful for designing the blast features, especially the maximum instantaneous charge. In some cases, this restriction can affect the length of the blastholes, their diameter,and any other variable.All these factors can have a huge impact on the price of the blasting project due to the specific studies required.

When there are insufficient data from the blasting area, it is necessary to use empirical prediction methods. Balsa (1989) proposed several interesting vibration transitivity laws based on hundreds of blasts carried out in different rock masses in Spain.Many empirical vibration prediction laws have been developed based on the maximum instantaneous charge or maximum charge per delay and the distance between the blast and the seismograph.However, they cannot include other characteristics of the blast(type of explosive,overlapping,delays,detonators,suitability of the blast) and the intrinsic features of the blast location. Several authors,such as Hudaverdi(2012)and Khandelwal and Saadat(2015),utilized empirical approaches to determine specific models depending on the rock mass type.

Different artificial intelligence (AI) approaches have also been proposed in recent years (Yu et al., 2020), using artificial neural networks to predict ground vibrations (Khandelwal and Singh,2009; Álvarez-Vigil et al., 2012; Monjezi et al., 2013; Iramina et al., 2018; Zhou et al., 2020) and probabilistic models (Zhou et al., 2021), providing interesting and reliable results.

While large quantities of data from blasts in open pit mining and quarrying can be obtained to determine the attenuation law,based on the data collected over time from many representative points,civil works usually lack this type of information, having scarce, or non-existent, preliminary information on rock mass behavior.Therefore, the analysis of the first blast is crucial for obtaining as much information as possible.

According to the standard analysis,the recording of one blast by a seismographer stands for one point in the peak particle velocity(PPV)-scaled distance (SD) graph, from which it is not possible to determine the specific vibration attenuation law. Nevertheless, it could be deduced from a single blast assuming the superimposition principle and signature-hole method used in several previous studies(Stump and Reinke,1983;Toraño et al.,2006;Hemant and Mishra, 2019). This procedure is faster and cheaper than other options currently used. Its application requires the following conditions and variables:a minimum number of blastholes,charge per delay, and distance from blastholes to the monitoring point in a wide range.Particular attention should be paid to the possibility of having a wave-front reinforcement line (Richards, 2008).

The aim of this study was to determine the vibration attenuation law from the monitoring of a single blast,a trench excavation with a rock mass consisting of sandstone and marl.In this regard,the case study has the ideal characteristics,i.e.the charge per delay and the distance from the blastholes to the seismographers vary along the trench.There are only two rows of blastholes,making the analysis easier. Hence, a new approach to determine the ground vibration attenuation law from data of only one blast is proposed, based on an empirical analysis of the vibrations related to a long linear blast.

2. Case study

2.1. A trench excavation for the project “Arteria Norte”

The blast studied was performed during the excavation of Arteria Norte, a buried water pipeline placed between La Pica and Pinzales villages in Asturias, Spain.

Arteria Norte is an underground facility with more than 11.5 km of pipelines.The system has been operating for 39 years,supplying 95,000 m3of water per day. The urgency of this renovation work was due to the continuous failure of the old pipeline. The new construction is placed parallel to the old one.

Based on the rock mass characteristics, the excavability was considered as moderate and in dry conditions,making it possible to use mechanical equipment in most areas(Tsiambaos and Saroglou,2010).Despite that,some other parts of the piping layout required blasting due to local rock mass changes and low performance of the mechanical excavation.Along the trace of the new project,there are a significant number of structures that need to be protected from the potential damage of the blasts (Fig.1).

2.2. Geological and geotechnical characteristics

The place is located in the Gijón-Villaviciosa basin, more specifically, the Purbeck facies of the upper Jurassic or Malm, with a Meso-Tertiary origin due to the sinking of the septentrional part of the Asturian region caused by two deep faults, one oriented in WNW-ESE and the other in NE-SW. Over the course of its history,this basin has alternated between episodes of depression and elevation, which led to series of marine, lake, and terrigenous sediments.

The ground was directly diggable with an excavator in many parts of the trench,using a hydraulic breaker hammer for stronger rocks. Nevertheless, both methods were inadequate in some parts of the trench with conglomerates, sandstone,and marl layers.

The conglomerate levels were studied in detail in order to characterize the rock excavability and design the blasting properly(Fig.2).The UCS was σc=45 MPa,and the rock mass quality varied from fractured rock mass with GSI = 35 and RQD = 40% to a more massive rock mass with GSI = 60 and RQD = 90%.

Fig.1. Scattered houses located near the trench.

An interlayer of sandstone and marl from the Jurassic period also required the usage of blasting techniques. As can be seen in Fig. 3, the gray marl was diggable by an excavator (it could be considered as a competent soil with rock-like structure with σc= 0.51 MPa), while the sandstone could be excavated by a breaker hammer(σc=3.42 MPa)in some cases.It was common to find stronger sandstone layers with a very low mechanical excavating ratio. Moreover, the plasticity of the marl made the performance of the breaker hammer diminish further. Fig. 3 also shows how the excavator was able to dig the topsoil but not the underlying sandstone.

The rock mass was only characterized in some parts of the total length of the trench due to a limited budget,a very complex terrain in some parts of the layout, and legal issues with the landowners.Thus, the empirical study of the vibrations gains importance,characterizing the rock mass by the parameters of the vibration attenuation law instead of its own mechanical properties.

2.3. Blasting design and control

Many buildings were scattered around the area where the blasting was planned,creating a potential issue with vibrations.On the other hand,the behaviors of the sandstone and marl regarding the ground vibrations were rather unknown.

Fig. 2. (a) General view of the trench and (b) two different levels of blasted conglomerates.

Fig.4 displays the layout of the pipeline in the studied area,the nearest building,and the location of the seismographs installed for the vibration monitoring. The location of the seismographs was based on the possible effect on these closest buildings, and they were accordingly positioned between the trench and the house.The minimum distance from the trench to seismographs S1 and S2 and the house was 25 m, 37.5 m, and 50 m, respectively.

A single blast of 148.5 m was conducted. It had two stretches with direction changes,one of 25.5 m southward and another one of 123 m northward. Ninety-nine pairs of blastholes were drilled,separated 1.5 m from each other. The pair of blastholes corresponding to each section was detonated simultaneously, and the delay between detonations was 42 m s.Under these conditions,the maximum instantaneous charge or charge per delay corresponds to a pair of blastholes. The whole blast lasted for about 4200 m s.

The blastholes were loaded with ammonium nitrate/fuel oil(ANFO)as column charge and one or two dynamite cartridges as a blaster at the bottom.The length of the blastholes varied depending on the topography and the depth required according to the project conditions. From south to north, the characteristics of the blastholes were as follows:

(1) Ten blastholes of 3 m length, 5 sections, with 3.68 kg per blasthole and a maximum instantaneous charge of 7.36 kg;

(2) Sixty-eight blastholes of 3.5 m length, 34 sections, with 5.7 kg per blasthole and a maximum instantaneous charge of 11.4 kg;

(3) Forty-six blastholes of 4 m length, 23 sections, with 5.36 kg per blasthole and a maximum instantaneous charge of 10.72 kg;

Fig. 3. (a) Gray marl and (b) sandstone in a prospecting excavation.

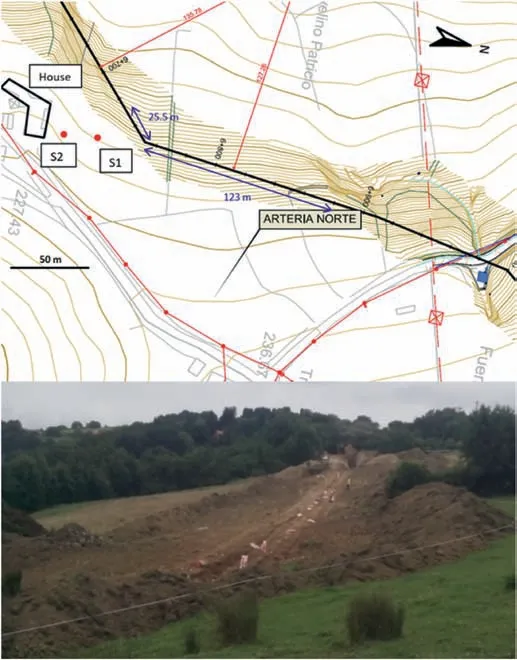
Fig. 4. Location of the seismographs and pipeline trace (upper) and trench viewed from S1 (lower).

(4) Forty-four blastholes of 4.5 m length, 22 sections, with 7.24 kg per blasthole and a maximum instantaneous charge of 14.48 kg;

(5) Thirty blastholes of 5 m length,15 sections,with 10.24 kg per blasthole and a maximum instantaneous charge of 20.48 kg.

The blasthole inclination was approximately 1:4(horizontal/vertical),and the distance between blastholes at the bottom was around 2 m. The stemming length was 2.25 m (2 m in blastholes of 3 m length).The bottom charge length was about 0.6 m,corresponding to two dynamite cartridges(only one cartridge for 3 m blastholes).The explosive charge for each pair of blastholes was chosen as a balance between the minimum amount necessary to break the rock and the maximum allowed by the ground vibration regulation.

3. Materials and methods

3.1. Vibration fundamentals

Ground vibrations are not only characteristic of a specific location but also depend on the performance conditions of the blasting.The ground vibration attenuation laws, or transmissivity laws,establish a relationship among the maximum explosive charge per delay,distance to the blasting,and vibration speed,with the aim of predicting the effects of the blasting depending on the variables to be tested.In this regard,one of the very first propagation equations was suggested by Morris (1950):

where A is the maximum displacement of the ground particles(mm); k is a constant dependent on the type of rock mass, which ranges from 0.57 for hard rocks to 3.4 for unconsolidated soils;W is the mass of the explosive charge (kg); and D is the distance between the blasting and the measuring point (m).

Blair and Duvall (1954) reviewed the ground vibration control techniques and suggested that the maximum displacement of the ground particles should be replaced by the sum vector of the particle velocity, which would mean a change in Eq. (1):

where v is the particle velocity (mm/s), and Kvris the empirical parameter depending on the rock mass characteristics.

Subsequent studies considered a relationship between the maximum particle velocity, or PPV, and the so-called scaled distance SD,which is defined as the distance divided by a function of the maximum charge per delay. It was considered that for a spherical symmetrical load, every linear dimension should be corrected by the cubic root of that explosive charge (Blair and Duvall,1954;Ambraseys and Hendron,1968;Dowding,1971;Agrawal and Mishra, 2019), while the PPV is considered the most reliable variable for predicting vibrations(De Cospedal,2019).The definition of SD is expressed by

where Q is the maximum instantaneous charge or maximum charge per delay(kg),and the parameter a varies depending on the researchers (Devine, 1966; Ambraseys and Hendron, 1968;Langefors and Kihlstrom,1978).

From a general perspective, taking the maximum particle velocity as the most characteristic parameter, it can be affirmed that the intensity of the seismic waves and the scaled distance follows the law displayed as

where K and n are the empirical parameters depending on rock mass characteristics.

Although Eq. (4) was proposed initially as an empirical relationship, Sambuelli (2009) proposed an analytical approach to support this empirical expression, pointing out that PPV depends on the geomechanical properties of the rock.

In the case of cylindrical explosive charges, it has been proven that the distances must be corrected by dividing them by the square root of the charge (Devine, 1966). Other researchers such as Holmberg and Persson (1978) and Ghosh and Daemen (1983) did not consider any special symmetry for the explosive load,but they considered the following general expression:

where α and β are the empirical constants for a specific location,and can be determined through a multiple regression analysis.

Singh and Vogt(1998)assessed some of the main transmissivity laws in a comparative research,finding out that all the laws differ in the prediction of the PPV at very long distances, and it is not possible to define the ground characteristics related to each law.It is also not possible to predict the velocity at very short distances,up to 3-4 times the drillhole diameter, which is crucial in the case of underground excavations.

On the other hand,Balsa(1989)studied several thousand blasts,presenting a statistic transmissivity law for different types of rocks in Spain. Data of the explosive charge, distance from the seismograph to the blasting point, type of triggering, and velocity and its component were used in the research. The general expression of the laws is represented as follows:

where the constants K, α, and β are obtained by empirical correlations that include all the other factors, mainly related to the characteristics of the rock mass excavated.The subsequent process is performed by blasting individual charges and measuring the velocity of the vibration for a known distance,with an adjustment of K,α, and β for Eq. (5).

These can be obtained with a minimum quadratic linear regression calculus.If the logarithmic-normal method is applied to the distribution of the points, it is possible to apply a security coefficient to the obtained law. The laws were calculated with a 90%confidence in this study, considering all types of triggering and components. The designated vibration frequencies of each type of rock mass were calculated as the mean of all the measurements(Table 1).

3.2. Ground vibration analysis and control

A complete ground vibration analysis following the Spanish standard UNE 22-381-93 (1993) includes two stages: before and after the blasting. The analysis before the blasting can be used to estimate the charge per delay and the type of ground vibration analysis/control necessary in order to comply with the regulations.

Following the standard UNE 22-381-93 (1993), the blast has to be represented by a point(D,QN)in Fig.5a,where D is the distance from the blasting to the structure,and QNis the normalized charge.The position of the point determines the type of study according to two lines that separate three areas in Fig. 5a. A point in the lower zone,Zone 1,represents a blast with no risk,because the charge is too small and/or the distance to the structure is long enough.In this case,the blasting is authorized without requiring any action.If the point is in the intermediate zone, Zone 2, the blast implies some risks, and it can be carried out as it has been projected only if the ground vibrations are controlled by a seismograph. Finally, if the representative point is in the upper zone, Zone 3, the blast cannot be carried out as it poses a risk because the charge per delay is too large or the distance to the structure is too small. In this last scenario, it is necessary to carry out a preliminary study with small explosive charges to determine the local ground vibration attenuation law and design the blast based on this determined law.

In the houses near the case study blasting, it is a reasonable decision to choose the possible maximum normalized charge within Zone 2. Considering that the distance is D = 50 m (the nearest house is only 50 m to the trench) and the normalized charge has to be less than 13 kg according to Fig.5a,the normalized charge QNis defined as

where FRis a coefficient depending on the rock properties and takes a value of 2.52, 1, or 0.4 for weak, medium, or strong rock mass,respectively;and FSis a coefficient depending on the structure to be protected and takes a value of 0.28 for structures of low sensitivity to vibrations(industrial areas),1 for medium-sensitivity structures(residential buildings), and 3.57 for structures very sensitive to vibrations (hospital, historic heritage buildings, etc.).

Assuming FR= 1 and FS= 1, the maximum charge per delay should be Q = QN≤13 kg. Based on previous experience, the maximum charge per delay in the blastholes nearest to the house is Q = 11.4 kg, in accordance with the Spanish regulation. Another analysis can be performed before blasting, and it consists of estimating the level of vibrations using a known vibration attenuation law.

Table 1 Transmissivity laws based on the rock mass characteristics (Balsa,1989).

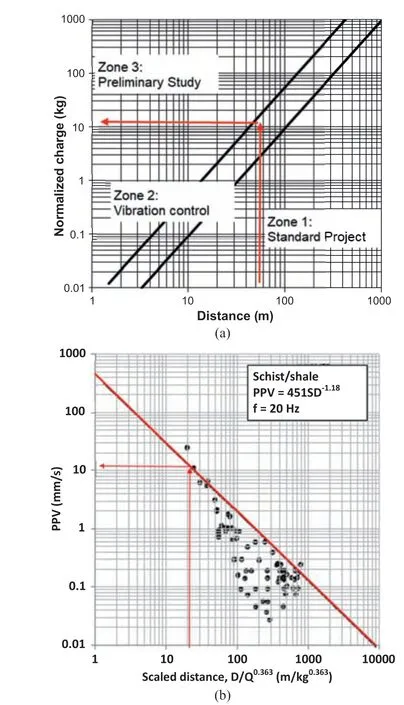
Fig. 5. Analysis of the ground vibrations before blasting.

The specific attenuation law for the case study of mixed rock mass, an interlayer of sandstone and marl, was not developed previously. The regular procedure would be to assume the rock mass behavior given by the known attenuation law and then design the blast,verifying,and modifying if necessary,the theoretical rock mass behavior after the first blast. However, in this study, it was assumed that the behavior would be similar to that of schist,based on some properties observed in situ rather than of its geological origin. This hypothesis was confirmed later by the results of the ground vibration control measures,as shown in Fig.5b,taking into account SD=50/11.40.356=21 m/kg0.356and PPV ≈12.4 mm/s.On the other hand,the expected frequency was rather low(f=20 Hz).

According to the blast design and regulations,it was mandatory to control the ground vibrations using the two seismographs detailed in Fig. 2 to measure the vibrations produced by the blast during all its way through the trench.

The equipment used for data acquisition consisted of two seismograph vibracords with three seismic channels (vertical, longitudinal, and transversal), which had an operational range of velocity of 0-150 mm/s and frequency of 2-250 Hz.The sampling rate was higher than 1000 samples per second according to the Spanish standard.The attachment of the equipment to the ground was performed following UNE 22-381-93 (1993). The detection limit of the seismographs was 0.01 mm/s.

The recording of S2 is shown in Fig. 6a. It is considered more representative of the vibration level than S1 because it is closer to the building to be protected and anchored in the bedrock on which the house is built. According to UNE 22-381-93 (1993), only two parameters are relevant when the blast occurs in Zone 2, i.e. the maximum particle velocity(PPV)and the fundamental frequency of the wave(f) determined from the analysis of the records with fast Fourier transformation (FFT). In this case, the representative parameters are PPV = 10.37 mm/s and f = 19 Hz, verifying that the behavior of the rock mass is similar to that of schist.

In order to characterize ground vibrations, UNE 22-381-93(1993) defines a damage prevention criterion as given in Fig. 6b,in which the representative point has to be plotted using f and PPV.The three lines in the figure define the maximum PPV allowable for each frequency in order to protect structures within groups I-III,equivalent to the three zones previously defined in Fig. 5a.

Analyses using both approaches, data from the actual blast(f = 19 Hz and PPV = 10.37 mm/s), and the estimation from the schist (f = 20 Hz and PPV = 12.4 mm/s) display that the blast is slightly below the group II curve, posing no risk to the house according to the Spanish standard.

3.3. Data processing

Apart from proving that the blasting was carried out within the limits of the law, the records of S1 and S2 provide information about the ground vibration attenuation law due to certain characteristics of this blast, its linearity, and the time lapse between blasthole initiation.

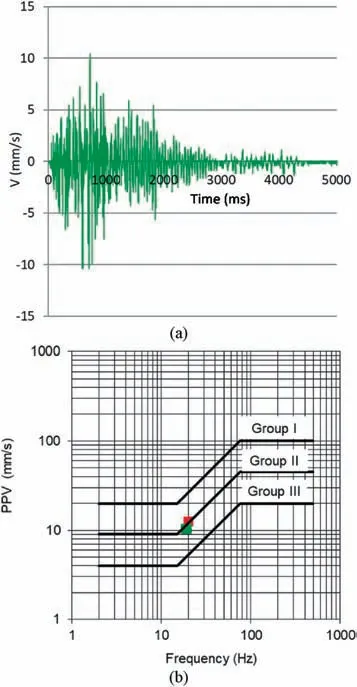
Fig. 6. Analysis of the ground vibrations after blasting.

Data from the three directions of the blast, i.e. vertical, longitudinal, and transversal, were analyzed to determine the seismic wave attenuation.However,only the vertical component was used in this study since the longitudinal and transversal components depend very much on the propagation direction. Data from each seismograph were extracted and processed to obtain the evolution of the velocity with time. Figs. 7 and 8 display the vertical components from S1 attached to the soil and S2 attached to the bedrock,respectively. It was obtained that PPV = 36.49 mm/s and PPV = 10.37 mm/s for S1 and S2, respectively. The fundamental frequency determined by FFT analysis was f= 19 Hz in both cases.

When the records in Figs.7 and 8 are observed in detail,it can be seen that all the peaks correspond to the detonation of a pair of blastholes, separated by approximately 42 m s, without the overlapping of the wave between blastholes initiated at different times.This fact is easily verified by analyzing a small period of time.Figs.9 and 10 show parts of the records from S1 and S2 between 2000 ms and 3000 ms.

Based on the information obtained from the graphs,it could be considered, in terms of vibration, that many different blasts occur in the trench due to the time span between detonations (42 ms).Therefore, the record is formed by a group of separated blasts at different distances from the seismographs, and this information can be used to define the transmissivity or attenuation law of the case study.The PPV generated for each pair of blastholes in S1 and S2 is represented as a function of time in Fig.11a and b,respectively.

Similarly,the distance from the pair of blastholes detonated at a given moment to S1 and S2 and the charge of these two blastholes can be expressed as a function of time (Fig.12).

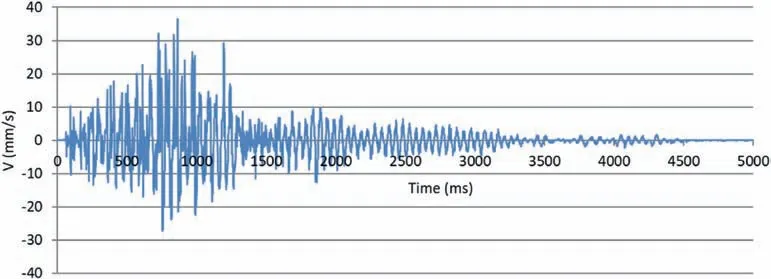
Fig. 7. Record of the vertical component from S1.

Fig. 8. Record of the vertical component from S2.

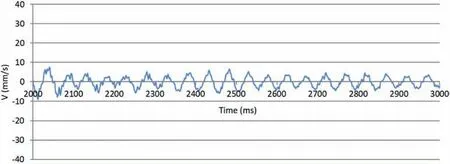
Fig. 9. Partial record of the vertical component from S1 in 2000-3000 ms.

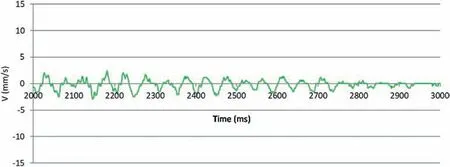
Fig.10. Partial record of the vertical component from S2 in 2000-3000 ms.

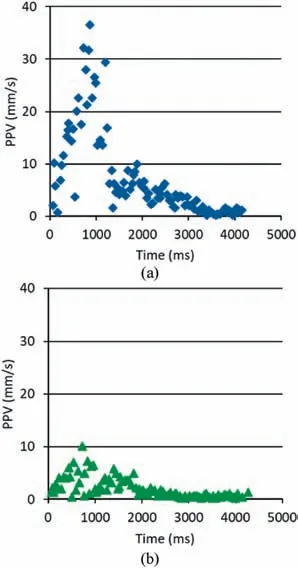
Fig.11. Peak values registered by the seismographs (a) S1 and (b) S2.

Subsequently, the transmissivity law can be calculated by combining the data from the previous graphs,since PPV is related to the maximum charge per delay and the distance between the seismograph and the blasting face in each instance. As there is no general transmissivity law for this type of rock mass,i.e.sandstone and marl from Purbeck facies,an adjustment of one of the statistical laws developed by Balsa (1989) was considered.

It has to be pointed out that the distance from the detonated blasthole to the seismographer varies in a relatively wide range,while the charge per delay is kept in a small range,between 10 kg and 15 kg in 80%of the cases,with an overall average value of 13 kg.This last value is used in the calculations in the following section.

4. Results and discussion

4.1. Ground vibration attenuation law

Fig. 12. (a) Distance from the instantaneous blast to the seismographs and (b)instantaneous charge.

The maximum values of the peak velocity for each blasthole from S1 (blue) and S2 (green) were used to obtain an empirical equation from which the wave attenuation law depending on the distance can be calculated(Fig.13a).The full attenuation law was obtained (blue line) using a single blast, which was a completely different approach from the traditional method, where it is assumed that each blast can only provide a single point of the attenuation law. The representative points were compared to other already stablished attenuation laws to verify the results(red line).

The shape of the point cloud suggests that there is an important component of non-elastic energy loss. In this regard, Ghosh and Daemen (1983) and Rai and Sigh (2004) suggested expressions to represent the decrease in PPV with distance. The approach from Ghosh and Daemen(1983)was considered most convenient for the case study (see Eq. (8)), assuming that the reduced distance corresponds to schist (SD = D/Q0.365）, where the exponent, 0.365, is very close to 1/3 (≈0.333)as suggested by the authors.

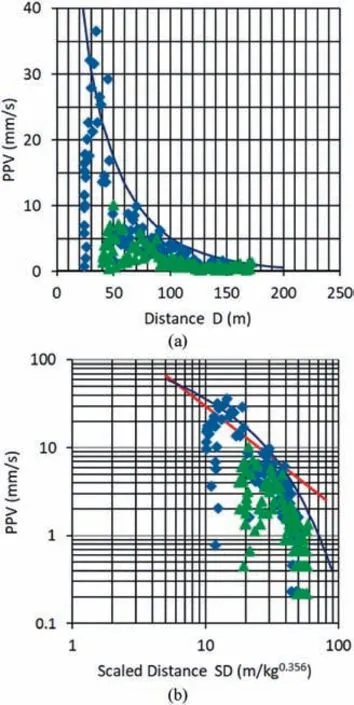
Fig.13. Relationships of(a) PPV-D and(b)PPV-SD.SD is calculated for schist. The blue line is the deduced attenuation law and the red line is the attenuation law after Balsa(1989) for schist.

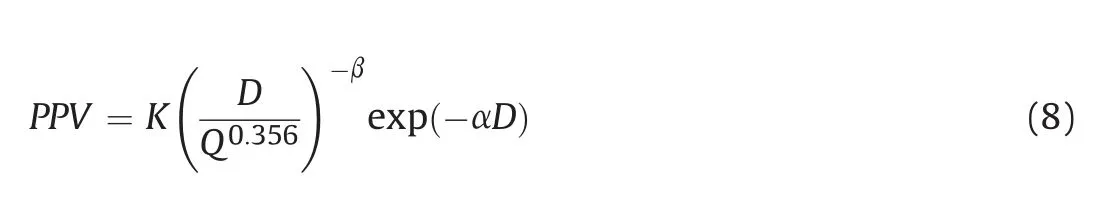
Applying natural logarithm and a least squares adjustment(with a correlation coefficient R2=0.63),the following values were obtained:K=50.2,β=0.418,and α=0.0183.Although the line best fits the point cloud, the enveloping line above the points is necessary, and the envelope position is reached by applying a coefficient to the K factor, vertically relocating the curve.

A confidence level of 90% was reached by multiplying K by 3,obtaining the following final values: K = 150.6, β = 0.418, and α=0.0183.Thus,the attenuation law for the rock mass of the case study is as follows:If the maximum charge per delay, Q, is known, then the curve obtained by Eq. (9) can be plotted as a function of D. In the case study,Q is a variable,but its mean value has been used in this case,i.e. Q = 13 kg. Subsequently, the expression that defines the envelope curve based on the empirical data is given as

As described above, the blast design was carried out assuming that the excavated rock mass consisting of sandstone and marl has a behavior similar to that of schist.In order to test it,the attenuation law as a function of scaled distance (SD) must be deduced. The attenuation law for schist according to Balsa (1989) is detailed in Eqs.(11)and(12),while Eq.(13)is reached by calculating D with Eq.(11) and then substituting it in Eq. (9).

It is noted that the vibration attenuation law would be given by Eq. (9) in this case. Eqs. (10) and (14) were only deduced for the corresponding graphs.It should also be stressed that this curve can be determined because the scaled distance SD varies in a sufficiently wide range of approximately 10-70 m/kg0.356.

The point cloud, the deduced curve from Eq. (14), and the attenuation law for schist according to Balsa(1989)are represented in Fig.13b.It is proven that the schist attenuation law could be used to predict the vibration level in this specific rock mass.Around 95%of the real values are under the value predicted by the schist law,which is in accordance with the level of confidence of this attenuation law. On the other hand, the actual frequency, f = 19 Hz, is consistent with the common frequency for schist(f=20 Hz).Once the real local curve has been obtained(Eq.(9)),it would be better to use it instead of other more general expressions, which is also useful for other parts of the trench and similar geomechanical conditions.

Fig. 14. Comparison between the deduced attenuation law (blue line), and the attenuation law after Balsa (1989) for (a) conglomerates and (b) quartzite (red lines).

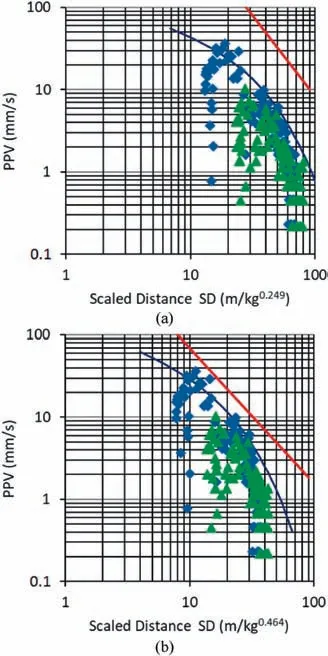
Fig. 15. Comparison between the deduced attenuation law (blue line), and the attenuation law after Balsa (1989) for (a) gypsum and (b) limestone (red lines).

4.2. Analysis with attenuation laws from other types of rock masses

It is interesting to compare the empirical attenuation law obtained in this study with other data and expressions from other types of rock masses gathered by Balsa (1989) that are commonly blasted.As can be seen in Fig.14,conglomerates and quartzite have attenuation laws that could be used to predict the PPV in the case study. However, these are completely different rock masses,stronger than sandstone/marl interlayer.This can be deduced from their natural frequencies, on average f = 30 Hz for conglomerate and f = 40 Hz for quartzite.

On the contrary, rock masses with typically low natural frequencies, similar to those observed in this study, such as gypsum with an average of f = 10 Hz or limestone with f = 25 Hz, have different behaviors regarding the PPV attenuation.The gypsum and limestone attenuation laws predict PPV values several times higher than the real ones,5-10 times in the case of gypsum and 2-4 times in the case of limestone (Fig.15).

The behavior of these four types of rocks (conglomerate,quartzite, gypsum, and limestone), although similar in some aspects, cannot be assumed to be equivalent to the real behavior of the sandstone/marl interlayer studied. Only the schist displayed equivalent characteristics compared to sandstone/marl interlayer,as its attenuation law can be used to predict the PPV and the natural frequency of the vibration. This similarity is based on similar geomechanical properties,regardless of the nature of the rock or its genesis, as stated by Sambuelli (2009) and Kumar et al. (2016).

5. Conclusions

In this study, an approach to define the transmissivity laws for ground vibrations in a single blast was determined. However, the results cannot be generalized, allowing the use of this approach only in the specific area of the case study.

The blast behavior was defined,as the wave approaches,reaches the peak vibration value,and starts decreasing as it moves furthers away.This information,together with the minimum distance from the measuring point to the trace and the explosive charge, can be used to calculate all the necessary empirical relationships. A procedure to determine and validate an approximation of the behavior of rock masses with the general transmissivity laws was established.

This methodology can be used as guidance in other cases,taking a step forward towards simpler and faster preliminary studies where explosives are required,being able to control the frequency and PPV according to national regulations.This would decrease the costs of the preliminary and control studies.

Although the general law proposed cannot substitute for a specific analysis of a case study, it provides a very reliable approximation, avoiding previous studies required by the governmental authority in some cases.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The present work was partially funded by Perforaciones Noroeste S.A. in the frame of the University-Company collaboration project FUO-068-17.