Kriging-based reliability analysis of the long-term stability of a deep drift constructed in the Callovo-Oxfordian claystone

Ngoc-Tuyen Trn, Duc-Phi Do,*, Dshnor Hoxh, Minh-Ngoc Vu, Gilles Armnd

a Univ. Orléans, Univ. Tours, INSA CVL, Lamé, EA 7494, France

b Andra, R&D Division, 92298, Chatenay-Malabry, France

Keywords:Reliability analysis Kriging metamodeling Time-dependent behavior Compressible material Callovo-Oxfordian (COx) claystone Long-term stability

ABSTRACT Callovo-Oxfordian(COx)claystone has been considered as a potential host rock for geological radioactive waste disposal in France(Cigéo project). During the exploitation phase (100 years),the stability of drifts(e.g.galleries/alveoli)within the disposal is assured by the liner,which includes two layers:concrete arch segment and compressible material. The latter exhibits a significant deformation capacity (about 50%)under low stress (<3 MPa). Although the response of these underground structures can be governed by complex thermo-hydro-mechanical coupling, the creep behavior of COx claystone has been considered as the main factor controlling the increase of stress state in the concrete liner and hence the long-term stability of drifts. Therefore, by focusing only on the purely mechanical behavior, this study aims at investigating the uncertainty effect of the COx claystone time-dependent properties on the stability of an alveolus of Cigéo during the exploitation period.To describe the creep behavior of COx claystone,we use Lemaitre’s viscoplastic model with three parameters whose uncertainties are identified from laboratory creep tests.For the reliability analysis,an extension of a well-known Kriging metamodeling technique is proposed to assess the exceedance probability of acceptable stress in the concrete liner of the alveolus.The open-source code Code_Aster is chosen for the direct numerical evaluations of the performance function. The Kriging-based reliability analysis elucidates the effect of the uncertainty of COx claystone on the long-term stability of the concrete liner. Moreover, the role of the compressible material layer between the concrete liner and the host rock is also highlighted.

1. Introduction

The French National Radioactive Waste Management Agency(Andra) is in charge of studying the disposal of high-level and intermediate-level long-lived waste (HLW and ILW-LL) in deep geological disposal (Cigéo project). Cigéo will be located at the border of the Meuse and Haute-Marne departments,nearly 300 km east of Paris. The host formation consists of claystone (Callovo-Oxfordian argillaceous rock-COx)lying between 420 m and 550 m in depth and exhibiting very favorable conditions for a repository of radioactive waste, as it generally has a very low hydraulic conductivity, small molecular diffusion, and significant retention capacity for radionuclide. The underground disposal facility will be divided into two sections depending on the type of waste (ILW-LL or HLW) and the type of excavation used to emplace the waste disposal packages(tunnel for ILW-LL and steel cased micro-tunnel for HLW). The ILW-LL zone is constituted of alveoli/galleries of about 10 m in diameter,which is planned to be excavated by tunnel boring machine (TBM)with an immediate installation of the liner.The ILW-LL cell’s liner is the concrete arch with a thickness of 0.5 m covered by 0.2 m of compressible material. The installation of the compressible material in the support system is currently regarded as an innovative and promising construction of the underground structure within the time-dependent geological formation thanks to its high compressibility (deformation more than 50% under stress lower than 3 MPa)to absorb the high convergence of the host rock.

This study aims at investigating the stability of an ILW-LL drift of Cigéo during the exploitation period by accounting for the uncertainty of the host rock behavior.The maximal stress evolution of the concrete liner is considered as the time-dependent indicator of the ILW-LL alveolus’ stability.

Actually, the time-dependent response of the ILW-LL cell is governed by the thermo-hydro-mechanical (THM) coupling.Indeed, the heat released from ILW-LL packages emplaced within the alveolus makes the temperature rise in the host rock and the structural elements (≤65°C in the concrete structure), which can induce the thermo-mechanical stress and the thermal pressurization phenomenon (Conil et al., 2020; Vu et al., 2020). Besides, the time-dependent behavior of ILW-LL drift is also controlled by the drainage from the intact rock to the wall, the desaturation of the rock close to the wall due to the ventilation during the exploitation phase, and shrinkage/swelling of COx claystone due to the desaturation/resaturation (Wang et al., 2021). However, it has been shown in different contributions (Camusso et al., 2020; Alonso et al., 2021) that the creep behavior of host rock has a preponderant role in the stress state of the concrete liner,while the effects of the heat loading and the pore water pressure change are marginal.

Therefore, this study focuses only on the uncertainty effect of the creep behavior of the host rock on the exceedance probability of critical stress in the concrete liner of the ILW-LL drift. Both laboratory tests at the sample scale and the convergence measurement in the Andra Underground Research Laboratory (URL) show that the time-dependent response of COx claystone exhibits a significant initial strain rate that decreases with time(Armand et al.,2013,2017). Advances in numerical models have been proposed to reproduce the observation of short- and long-term behaviors of COx rock, e.g. non-local anisotropic elasto-viscoplasticity (Manica et al., 2021a, b), second gradient anisotropic elastoplasticity(Pardoen and Collin,2017),double phase-field elastoplastic damage model (Yu et al., 2021), and elastoplastic model combined with weakness planes (Souley et al., 2020). Characterized by various parameters (e.g. larger than 20 parameters), whose physical meaning and calibration are not simple to be evaluated, these sophisticated models are not feasible for the reliability analysis. In this work, the use of the well-known Lemaitre’s model is motivated, on one hand, by its simplicity (characterized by only three parameters easily calibrated from creep tests) and, on the other hand, by its accuracy to describe the long-term behavior of host rock (Souley et al., 2017a). Available laboratory triaxial creep tests under different deviatoric stresses are taken to estimate the uncertainty of viscoplastic properties of COx claystone.

The stability of the concrete support of underground structure during the period of exploitation(～100 years)is crucial to ensure the functionality of the mechanical system within the tunnel (i.e.the movement and deposit of waste packages). In this context, a delay effect due to the time-dependent behavior of host rock on the stability of structures is critical and must be taken into account in the optimization design of these constructions. The widely used deterministic (or semi-probabilistic) design methods in geotechnics based on several partial safety factors for considering different uncertainty sources (e.g. geomaterial property uncertainty,loading uncertainties,etc.)have pointed out several limits in rock engineering (Spross et al., 2018). The difficulty lies in the uncertainty quantification of the delay effect and its propagation on structural stability.This is mainly because the experimental tests in the laboratory and/or in situ can only be conducted within a short period as compared with the service life of almost all structures,particularly with those related to the deep geological nuclear waste disposal.

In the last decades, the reliability analysis has been received much attention, and its progress toward practical applications in geotechnical rock engineering has been largely remarked (Wang et al., 2013; Contreras and Brown, 2019; Siacara et al., 2020).Especially,in many contributions(Laso et al.,1995;Schweiger et al.,2001;Mollon et al.,2009;Langford and Diederichs,2013;Lü et al.,2013), the probabilistic-based method has successfully been applied to the stability analysis and the optimization design of tunnel support in the rock mass. Following that, the Monte Carlo simulation (MCS), the first- or second-order reliability method(FORM/SORM),and response surface method(RSM)are among the most chosen probabilistic methods. However, these contributions dealt almost exclusively with the short-term behavior of underground excavation by accounting for the uncertainty of the elastoplastic parameters of the host rock. Recently, Do et al. (2020)evaluated the failure probability in time of a deep tunnel excavated in a viscoelastic rock by using the MCS.Their study revealed a critical effect of the uncertainty of the viscoelastic parameters on the long-term stability of the tunnel. Ignoring the uncertainty of the time-dependent characteristic of the rock mass can thus lead to an underestimation of the long-term structural stability of underground structures.

Due to the time-demanding computation of the deterministic problem as well as the non-linear behavior of the viscoplastic COx rock, the Kriging metamodeling technique is chosen in this study for the reliability analysis of the ILW-LL alveolus. An extension of the well-known AK-MCS (active learning reliability method combining Kriging and MCS) method is proposed. In comparison with the massive number of trials in the MCS method,this Kriging metamodel allows a fast computation by using a very reasonable number of direct numerical simulation to solve the deterministic problem.This method provides hence a useful and performant tool in the reliability analysis and optimization design,especially when the response of complex structures is only assessable by the numerical simulation, such as the present case of deep drift in the viscoplastic rock.

The paper is organized as follows. In the next section, the geometry, loading (in situ stress), and the constitutive mechanical behavior of all components (host rock, concrete liner, and compressible material)as well as the uncertainty quantification of the long-term mechanical properties of COx claystone are presented.In Section 3,the Kriging metamodeling technique based on the modified AK-MCS method is described.In Section 4,numerical investigations on both the deterministic and the reliability analysis problems are provided.In addition to the uncertainty effect of COx rock, sensitivity analysis on the thickness of both liners (concrete and compressible material) and the compressibility of the compressible layer is also carried out in the reliability analysis.Discussion and some critical remarks derived from these numerical results are then pointed out. Conclusions and perspectives are drawn in the last section. Notably, throughout the paper, the light symbols denote scalars, and the bold images indicate the secondorder tensors(as a vector or a matrix).

2. Description of the studied problem

2.1. Geometry and loading

At the position of the Meuse/Haute-Marne (M/HM) URL, the initial stress state is characterized by three principal stresses: vertical stress σvcorresponding to the ground weight, minor horizontal stress very close to the vertical stress(σv≈σh≈12.5 MPa),and major horizontal stress (σH≈1.3σh) (Armand et al., 2013).According to the design of the Cigéo project,the alveoli dedicating to store the nuclear waste (ILW-LL and HLW) will be planned to excavate following the major horizontal stress(i.e.the stress in the tunnel section is quasi-isotropic).This choice is undertaken due to the long-term safety of nuclear waste management. The length of an ILLW-LL alveolus (about 500 m) is much greater than its diameter (about 10 m); thus, a plane strain model is adopted in this study.

It is assumed that the parallel drifts are separated enough to ignore their mechanical interaction, i.e. this study limits to an individual drift behavior.Fig.1 illustrates one-quarter of the adopted two-dimensional (2D) plane strain model of drift, considering the symmetric conditions. Following that, to simulate the mechanical behavior of the circular drift with 5.05 m of radius, the width and the height of 55 m are taken. Concerning the symmetric boundaries, the normal displacement is fixed. At the top and the right interfaces,normal stress σ0=12.5 MPa,which is approximated the measured vertical(σv)and minor horizontal(σh)stresses at the M/HM URL, is imposed. It is worth noting that our proposed methodology can be applied in the general case of anisotropic initial stress state without any additional complexity.

The considered drift is supported by a concrete lining(the class of concrete is C60/75 according to the European Code classification), which is separated from the rock mass by a compressible layer. The drift excavation is assumed to be instantaneous whilst the simultaneous installation of the compressible liner and the final concrete support corresponds to a deconfinement ratio of 85%.The role of the compressible support is to absorb the convergence and to reduce the transmitted stress to the concrete lining which is supposed to be linear elastic.

2.2. Time-dependent behavior of COx claystone

In this work,Lemaitre’s model is considered to express the timedependent behavior of host rock.Most of the authors dealing with the time-dependent behavior of COx claystone have proposed various (elasto-) viscoplastic models (Seyedi et al., 2017;Stavropoulou et al.,2020).Even if other sophisticated models could be considered for specific features of COx rock behavior (e.g.Armand et al.,2017;Mánica et al.,2017;Seyedi et al.,2017;Souley et al., 2020; Stavropoulou et al., 2020), the viscoplastic model of Lemaitre is sufficiently accurate for long-term design purposes and with a limited number of constitutive parameters.

By neglecting the (thermo-) hydro-mechanical coupling effect,the total strain tensor εtotreads

where εeand εvindicate the elastic and viscous strain tensors,respectively.The viscous strain rate（˙εv）is expressed as a function of deviatoric stress tensor thanks to Lemaitre’s law:

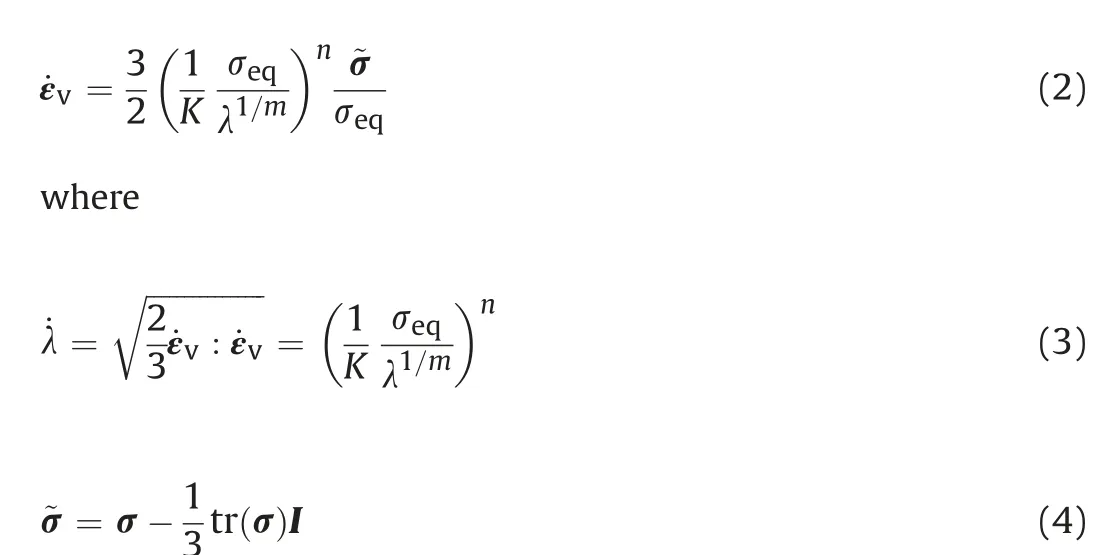
where σ and ～σ are the stress tensor and its corresponding deviatoric part, respectively; and I indicates the second-order identity tensor. The over-dot denotes the time derivative while tr（σ） designates the trace of the stress tensor. Also, λ and σeqmean the accumulated viscous strain (i.e. the time-dependent distortion strain) and the equivalent (or the Von-Mises) stress, respectively.The positive triple (K, n, m) is the set of mechanical parameters characterizing the long-term behavior of the material following the Lemaitre model.

Posing α=n/m and after some developments,the accumulated viscous strain can be explicitly expressed as a function of equivalent stress and time:

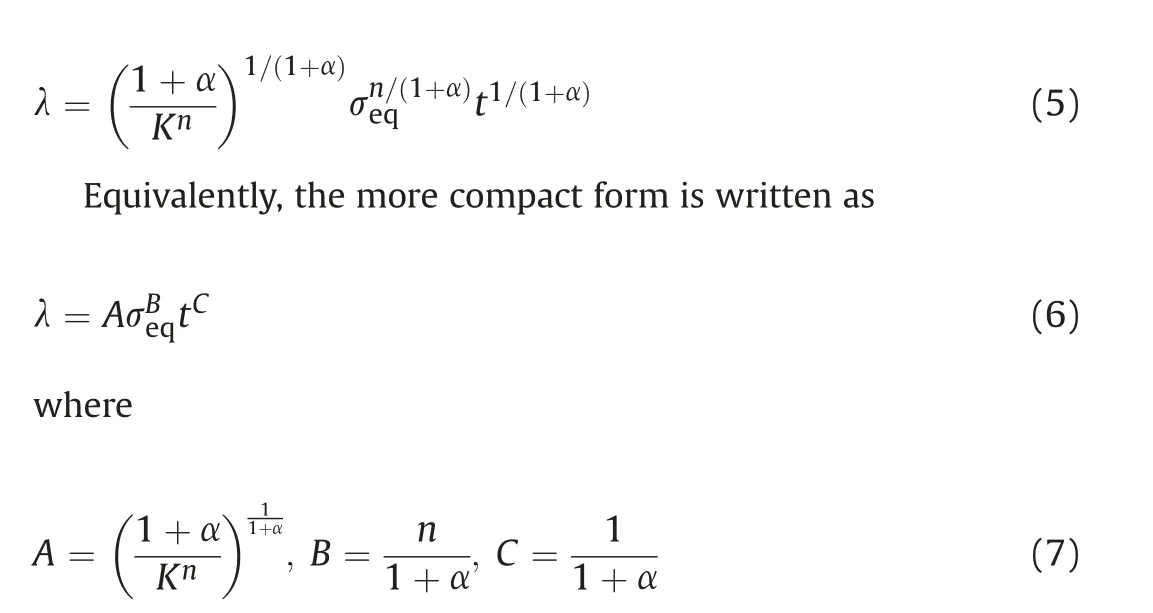
Besides, the positive triple is then inferred based on the parameters A, B, and C as follows:

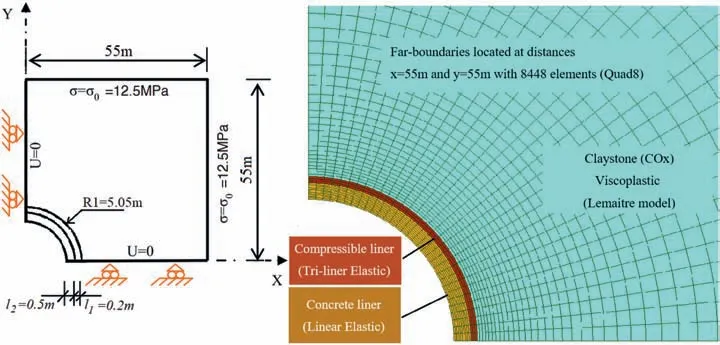
Fig.1. 2D plane strain model of drift supported by the outer compressible and inner concrete liners in viscoplastic COx rock.

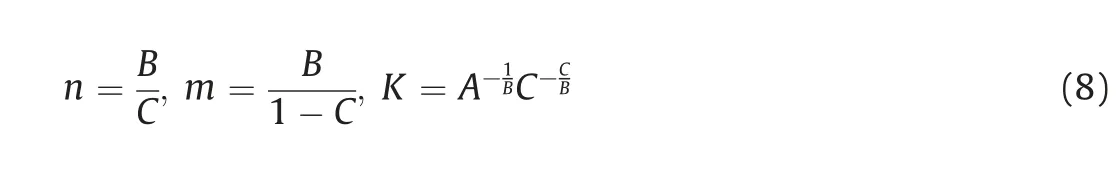
2.3. Tri-linear elastic model of the compressible liner

The compressible material used as the outer liner to reduce the overstress of the inner lining of drift has already been widely used in various research projects (Lombardi, 1981; Strohhäusl, 1996;Schneider et al.,2005;Billig et al.,2007;Ly,2018;Gasbarrone et al.,2019).At the M/HM URL,different types of compressible materials have been tested,and the primary feedback from the experimental program reveals their immense benefits (e.g. reducing the transmitted stress to the concrete liner of drift). Owing to a high void ratio, the mechanical behavior of the compressible materials usually presents a non-linear characteristic due to the pore collapse mechanism under compressive loading.For example,Fig.2a shows the results of a compression test performed on a specific compressible grout. The material is constituted by expanded polystyrene beads and foam to achieve compressibility up to more than 50%of its initial volume(Billig et al.,2007).The stress-strain curve from these experiments can be captured in three stages.Following that, the curve shows an elastic behavior when the volumetric deformation of the compressible material is small.Then a plastic behavior represented by a strain hardening can be observed, while the last stage characterizes the stiffening of the material after the depletion of its porosity.

Many attempts to reproduce the mechanical behavior of the high porous compressible materials have been conducted. For example, in Souley et al. (2017b), an elastoplastic constitutive model was proposed. In this model, the Drucker-Prager criterion and a strain hardening based on an exponential function of the plastic distortion have been applied.Besides,the yield function,the hardening, and the densification mechanism are explicitly related to the pore collapse mechanism (e.g. volumetric plastic strain due to the hydrostatic failure).

For reasons of simplification, a tri-linear elastic behavior was adopted here for the compressible support layer (Fig. 2b). This simplification is acceptable when in our analyses of drift, the compressive stress state in this compressible liner increases monotonically with time. It is worth mentioning that, under the monotonic loading condition, the stress-strain curve provided by our tri-linear elastic model can well fit the experimental data(Fig. 2a).

As a function of the volumetric deformation, the tri-linear elastic model is characterized by the triple values of elastic modulus (Ec1, Ec2, and Ec3) and is expressed in the following form:

The Poisson’s ratio of the compressible material is so small and presents a neglected impact on the drift response. Thus, it can be taken equal to zero(νc=0).For the numerical simulations,this trilinear elastic model has been implemented in the Code_Aster(EDF,2017).

2.4. Choosing the failure criterion

The reliability analysis aims at estimating the failure probability of structure that its responses exceed one or multiple failure criteria by accounting for the propagation of uncertainty of different input parameters.A failure criterion can be mathematically expressed by a limit-state function (LSF) g(x) (also called the performance function).The structure fails when the value of LSF is less than zero(g(x)≤0).In the recent contribution of Do et al.(2020),two timedependent performance functions were proposed to define the failure state of a deep tunnel excavated in a rheological rock.Following that,the failure of the tunnel can be investigated for the allowable convergence and/or the allowable stress in the system of liners.

Fig. 2. (a) Stress-strain curves of a compressible material under the oedometric test (Billig et al., 2007); and (b) Tri-linear elastic model of the compressible material versus volumetric deformation.

Since there is the presence of the outer compressible liner, the high convergence on the tunnel wall can be accepted,and our work focuses mainly on the prediction of failure probability of the concrete liner of drift. We consider that the concrete liner fails when the maximum equivalent stress ql（x）overpasses the allowable stress σclof the constitutive material. The corresponding performance function is then defined as follows:

where the vector x denotes the set of random input variables in the reliability analysis. In comparison with the artificial constitutive materials of the compressible and concrete liners, the uncertainty of the mechanical properties of the natural COx rock is much higher. Consequently, only the uncertainty of the host rock properties is counted in this work.

According to the discussion in Do et al.(2020),for the case that the tunnel response over time is monotonic, the time-dependent reliability analysis can be done similarly to the time-invariant problem by calculating only the probability of failure at a chosen design lifetime of the tunnel.The failure probability of the concrete lining of drift is measured at a period of 100 years, which corresponds to the period of exploitation of the deep geological repository, and hence in Eq. (11), the time parameter t is omitted.

It is important to point out that the non-linear behavior of the viscoplastic COx rock is the reason that the performance function in Eq. (11) cannot be expressed explicitly in the spaces of random variables but only be numerically evaluated at each selected subset of x.

2.5. Uncertainty quantification of mechanical properties of COx rock

In general, the sources of uncertainty of geomaterials can be classified into two groups. The first one, namely the epistemic uncertainty, is associated with the scarcity of data (quality, quantity, specification), and it comes from different stages of sampling preparation, transport, and testing procedure. The second one,called aleatory uncertainty,refers to the inherent spatial variability of rock.Regarding the COx claystone,the inherent variability of the mineralogical composition of this host rock, in addition to the scarcity of high-quality data, can contribute to a significant uncertainty of its mechanical properties.

In the present work, the uncertainty of COx rock properties is quantified from data measured in the laboratory on natural samples obtained from the main level of M/HM URL. According to the contribution of Armand et al. (2017), we assume that the mean value and standard deviation are 6 GPa and 3.5 GPa for Young’s modulus,respectively.Note that the influence of the Poisson’s ratio of rock mass on the behavior of drift is quite moderate as compared with the impact of the other parameters. Thus, its mean value(ν = 0.29) is used in this work as a deterministic parameter by ignoring its uncertainty.

Regarding the uncertainty quantification of the long-term mechanical properties of COx formation, this topic has not yet beendiscussed in the literature.So far,a universal constitutive model to accurately characterize the time-dependent behavior of COx rock does not exist. Additionally, the number of creep tests carried out on the samples of the same level and with the same condition seems very limited from the statistical point of view.

Table 1 Confining pressure and deviatoric stress of seven triaxial creep tests performed on COx rock.

As the first attempt to quantify the uncertainty of the long-term mechanical properties of COx claystone, in this study, we use the data of seven triaxial creep tests corresponding to seven applied deviatoric stresses performed on the samples taken from the same geological horizon (Armand et al., 2017; Seyedi et al., 2017). The information about the confining pressure and deviatoric stress of each triaxial creep test is summarized in Table 1, while for more details of these tests, the interested readers can refer to Armand et al. (2017) and different references cited therein. The calibration of the viscoplastic parameters of Lemaitre’s model is conducted by using the compact form expressed in Eq. (6). Following this equation, the inverse analysis to determine the three parameters A, B,and C can be carried out by fitting the data of at least two creep tests under two different applied deviatoric stresses (Debernardi and Barla, 2009). Since two creep tests are performed with the same deviatoric stress(see Table 1),thus totally,the statistical analysis of the obtained results of three parameters A, B, and C is conducted with 88 samples generated from at least two tests. The mean and standard deviation of the viscoplastic Lemaitre’s parameters are summarized in Table 2.As a function of the applied deviatoric stress and time,the exponential parameters(i.e.the parameters B and C),which characterize the non-linearity of COx rock, present the corresponding mean values of about 2.05 and 0.17, respectively. The coefficient A presents the most considerable uncertainty represented by the highest coefficient of variation (COV) (about 87.5%).Our analysis also exhibits the correlation between these three parameters(see Table 3).More precisely,a relatively significant anticorrelation between the coefficients A and B characterized by a negative value of -0.72 is stated. The other correlations (for example, between A and C or between B and C) seem weaker and are not taken into account in our reliability analysis.Following the histograms captured in Fig.3,a log-normal distribution is adopted for these parameters. This chosen distribution avoids the negative value of Lemaitre’s model parameters (notably in the case of the coefficient A with high COV) generated from the sampling process in the reliability analysis.

As an example,Fig.4 presents the results of a triaxial creep test with the applied deviatoric stress of 27.75 MPa and confining pressure of 12 MPa,which are simulated from the mean values and 1000 random sets of the three parameters A,B,and C of Lemaitre’s model. Note here that the number of 1000 random sets of the Lemaitre’s model parameters is chosen just for the illustration purpose of the simulated triaxial creep test. But for the reliability analysis (by using the MCS for example), much higher random samples (about one million) will be taken as detailed in the next section.

The comparison of the numerical result using the mean values of A,B,and C,and the experimental data measured up to about 90 d(Fig. 4a) illustrates the correct tendency. However, due to the uncertainty of the long-term mechanical properties, the viscous deformation in COx rock may be higher than 10 times the ones measured with the mean values (Fig. 4a and b). It is important tonote here that the calibration and the corresponding statistical analysis of the long-term mechanical properties of COx rock are conducted with the creep tests performed for about 3 months.Consequently, an extrapolation of the viscous deformation to 100 years(Fig.4b)must also present another source of uncertainty that may underestimate or overestimate the corresponding results of the reliability analysis.

Table 2 Statistical values of the Lemaitre’s model coefficients calibrated from 88 samples taken from seven creep tests on COx rock.

Table 3 Correlation matrix between the calibrated coefficients of Lemaitre’s model.

2.6. Chosen deterministic parameters

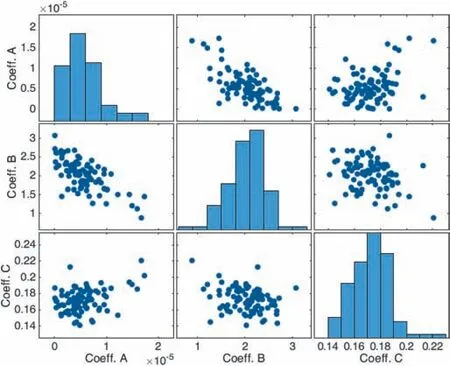
Fig. 3. Result and histogram of Lemaitre’s model parameters calibrated from 88 samples.

Herein the deterministic parameters like the thickness (l1)and mechanical properties of the tri-linear elastic compressible material (Ec1, Ec2, Ec3, εv1) as well as the elastic moduli of concrete C60/75 (El, νl) are chosen for the numerical applications and are summarized in Table 4. Notably, the mechanical properties of the compressible material of the outer liner are calibrated from the oedometric tests of the compressible grout(Billig et al., 2007).

The values of the other deterministic parameters, such as the thickness of the final support (l2) and the limitation (εv2) which separates the second and third stages of the tri-linear elastic model of compressible material, will be chosen in the context of a parametric study. Regarding the contrast of Young’s modulus between the second stage and the other stages,the parameter εv2represents,in fact,the compressible potential of the first support layer of drift to adsorb the high time-dependent convergence of host rock.

3. The methodology of Kriging-based reliability analysis

The application of the probabilistic approach to the stability analysis(Li and Low,2010;Lü et al.,2011,2013;Lü and Low,2011;Langford and Diederichs,2013)and optimization design(Laso et al.,1995; Mollon et al., 2009; Tran et al., 2020) of underground structures has been intensively undertaken since the last two decades. The most well-known method may be the MCS or crude MCS, which could provide an accurate estimation of the failure probability and has been regarded as the benchmark to validate the other probabilistic methods. Since the crude MCS requires a massive number of evaluations of structure response,it seems only to be appropriate in case that the closed-form solution is available(e.g.Do et al.,2020).Nevertheless,due to the complex behavior of rock(e.g.the case of drift constructed in the non-linear viscoplastic rock in this study), in most cases, structural behavior is only assessed through numerical calculation. An appropriate approximation method that could reduce the required number of timeconsuming numerical simulations is preferred. For example, in Wang and Shan (2007), Lü et al. (2013), and Tran et al. (2020), the scholars used the RSM to approximate the LSF,while the SORM was chosen to estimate the failure probability. Although the powerful RSM was demonstrated in the short-term reliability of the tunnel,this method can fail when the LSF is highly non-linear,non-smooth,or multimodal (multiple most probable points (MPPs)) (Huang et al., 2017).

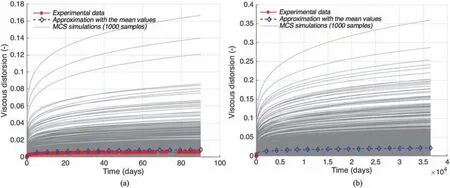
Fig. 4. Comparison of the experimental data (red curve)of a creep test with approximation using the mean values (blue curve)and the MCS using 1000 samples (gray curves)of three coefficients A, B, and C of Lemaitre’s model (a), and extrapolation to 100 years (b).

Table 4 Fixed values of deterministic parameters in the numerical investigations.

Many other advanced probabilistic methods have been proposed in the literature. Generally, the chosen approach aims at establishing a metamodel (or surrogate model), which approximates the implicit LSF by a mathematical function. The reliability analysis is then conducted on the built metamodel (by using, for example, the classical MCS sampling method), which allows fast computation with high accuracy.The interested reader can refer to Wang and Shan (2007), and different references cited therein for the details of various surrogate models (e.g. Kriging, radial basis function (RBF), artificial neural network (ANN), support vector machine (SVM), and polynomial chaos). In this work, the Kriging metamodeling technique is chosen for our reliability analysis of drift thanks to its flexibility in interpolating the sample points and high accuracy,notably for non-linear problems,according to Wang and Shan(2007).More precisely,a modification of the well-known AK-MCS method(Echard et al.,2011;Do et al.,2021),as detailed in the dissertation of the first author of the present paper(Tran,2020),is chosen. This modified AK-MCS method will be briefly synthesized below as well as in Appendix A.

Firstly developed by Krige (1951) and then theorized by Matheron (1973), the Kriging metamodeling technique approximates the implicit LSF by carrying out a Gaussian process:

where d is the dimension of the random variable vector x,and xiis the i-th component of x.

In fact, due to the stationary character of the Gaussian process,for each dimension of the vector x, the correlation functions depend only on the relative positions of two inputs characterized by a scale parameter θi(i = 1, 2, …, d).

The calibration of the unknown parameters σ2Z，β， and θ can be done through an optimization process by using the results evaluated at different observation points (also called training points)obtained from the design of experiment(DoE)step.The resolution of this optimization problem has mainly been discussed in the past and was successfully implemented in some software.In this work,the available MATLAB toolbox DACE (Lophaven et al., 2002) was used.

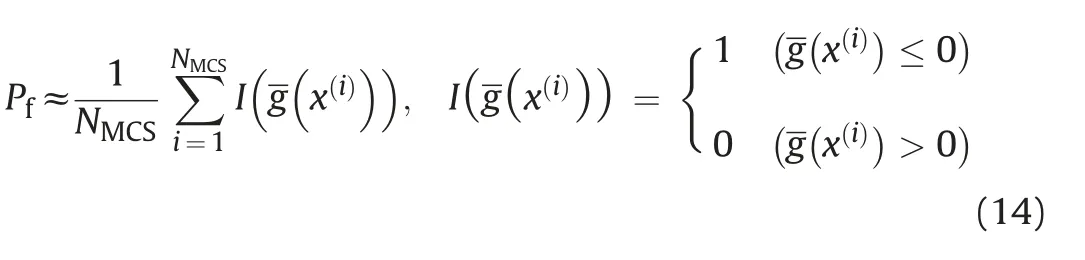
where NMCScounts the random samples that are generated for the estimation of failure probability by the MCS.

The probability evaluated by Eq. (14) depends on the Kriging metamodel, which is constructed from the results of the direct evaluation of the performance function at the training points of DoE. Thus, to derive the final result of probability, an iterative procedure is carried out. Following that, at each iteration, a subset of new training points can be chosen(based on a so-called learning function) to enrich the DoE. The process is continued until the obtained probability satisfies a stopping criterion. To simplify the presentation, our developed learning function and the chosen convergence criterion are presented in Appendix A(the interested reader can refer to Tran(2020)for much more details).For the sake of clarity, Table 5 summarizes the principal steps to conduct the Kriging-based reliability analysis using the modified AK-MCS method.

4. Numerical applications

4.1. Deterministic problems

Before analyzing the results obtained from the reliability analysis,let us discuss the behavior of the concrete liner extracted from the direct numerical simulations. The results of this so-called deterministic problem are of the primary importance for understanding the drift response before accounting for the uncertainty of the mechanical properties of the host rock.

For this aim, the mean values of the short- and long-term mechanical properties of rock mass are taken in this first simulation while the compressible potential of the first support layer is fixed at εv2= 0.4.

As the first observation, it is worth pointing out that the numerical simulations present a maximum of equivalent stress at the inner radius of the concrete liner.At the same time,the volumetric deformation is uniform in the whole layer of the compressiblesupport (Fig. 5). This expected result is consistent with different assumptions adopted, notably the hypothesis of isotropic hydrostatic stress at far-field and isotropic homogeneous material of components in the considered problem.By varying the thickness of the concrete liner (l2), the results exhibit a quite significant decrease of the maximum equivalent stress in this last support element (Fig. 6a and b). The mean values of the viscoplastic rock induce in the compressible liner a low volumetric deformation which is mostly smaller than the compressibility εv2= 0.4 (see Fig. 6c and d). By changing now the compressible potential εv2of the outer liner, we can observe in Fig. 7 that the maximum equivalent stress in the concrete liner seems constant when εv2≥0.015.The result of equivalent stress presents the highest value with the case εv2= 0.015. Notably, this latter value presents in the particular case （εv2= εv1= 0.015） in which the first support layer of drift loses the compressibility and is characterized by only one elastic modulus (Ec= Ec1= Ec3).

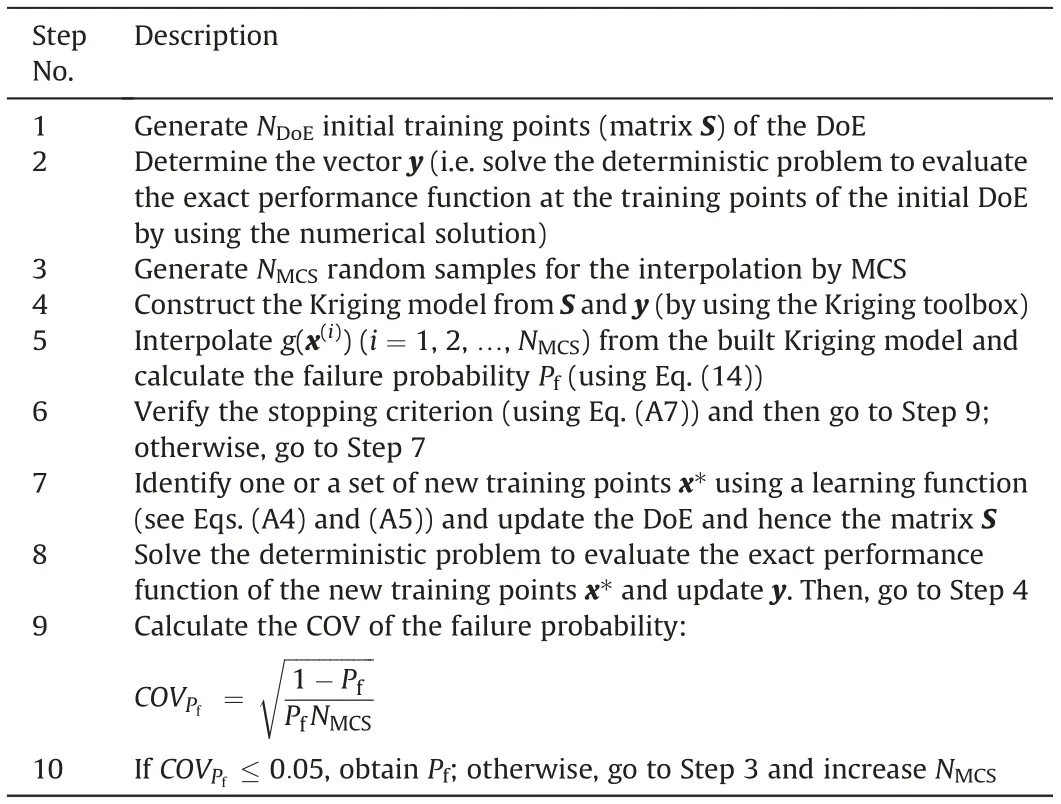
Table 5 Principal steps of a Kriging-based reliability analysis using the modified AK-MCS method.

To better understand the effect of rock mechanical properties on the behavior of the final support of drift, we present in Fig. 8 the results of another deterministic analysis in which a random set(noted as set1)of the COx rock properties is taken among the samples generated in the reliability analysis as detailed in the next section.More precisely,the chosen values of parameters A,B,and C,and Young’s modulus E of this set are respectively equal to about 1.7,1.3,1.1, and 0.7 times of their mean value (i.e. Aset1= 8.415 × 10-6,Bset1=2.647,Cset1=0.192,and Eset1=4.253 GPa).Corresponding to these mechanical properties of the massif, which are more critical than those in the case of using mean values,the results captured in Fig.8 reveal now the important effect of εv2on the time-dependent behavior and on the maximum equivalent stress at 100 years in the concrete liner (Fig. 8a and b). Following that, a smaller value of compressible potential εv2induces a significant increase of compressive stress in the final support element of drift. This is because,in the case of lower compressible potential,the volumetric deformation in the compressible support exceeds this limited value between the second and third elastic stages (i.e. εV> εv2), and the compressible material works with its highest elastic modulus at the rigidification stage(Fig.8c and d).

The results of the maximum equivalent stress in the concrete liner of drift (calculated with two sets of mechanical properties of COx rock: the mean values and set1) exhibit a great difference.Thus, a parametric study is then undertaken to investigate the influence of each parameter of COx rock properties on the response of the concrete layer at 100 years.This study is investigated by varying each parameter of interest while the other mechanical properties are maintained at their corresponding minimum, maximum, or mean values. Instead of using a 95% confidential interval of the distribution, the minimum and maximum values of each mechanical parameter are taken from 106random samples, which are generated for the reliability analysis as detailed in the next section.It is important to note that the anti-correlation of two parameters A and B of Lemaitre’s model (see Section 2.4) is counted in these random samples. However, in the present deterministic study and for simplification purposes,we ignore the anti-correlation of these two parameters by accepting the set containing both their maximum and minimum values.In this parametric study,the inner liner’s thickness and the outer liner’s compressibility are fixed with l2= 0.5 m and εv2= 0.4, respectively.

In general, one can state that, with respect to a higher value of one of the long-term mechanical parameters(i.e.either coefficient A or B or C),the maximum equivalent stress in the concrete element tends to increase (see Fig. 9a-c). This phenomenon seems to be consistent with the fact that, under a constant deviatoric stress applied, the increase of one of these parameters yields a higher viscous deformation, according to Lemaitre’s model expressed in Eq. (6). However, an evident tendency is difficult to be captured regarding the effect of the short-term mechanical properties of COx rock(i.e.Young’s modulus),as shown in Fig.9d.It can be explained by the interaction in a non-linear manner between the convergence of the viscoplastic rock and the reaction from the support system that generates in rock mass a redistribution of stress state represented by a variation of the deviatoric stress with time at a specific point of the host rock.This redistribution depends strongly not only on the short-and long-term mechanical properties of host rock but also on the time-dependent reaction loading of the support system,which in turn depends on the rigidity of both liners. Especially, it can be stated from this parametric study that the maximum equivalent stress in the concrete liner can vastly exceed the elastic limit of the concrete class C60/75. Note that in the typical civil engineering application,a compressible resistance about 60%of the concrete mark is mostly accepted as the elastic limit in the serviceability limit state design of the concrete elements as proposed in European Code 2 (EC2). Beyond this limit, one considers that cracking under compressive loading can occur in the concrete structure.

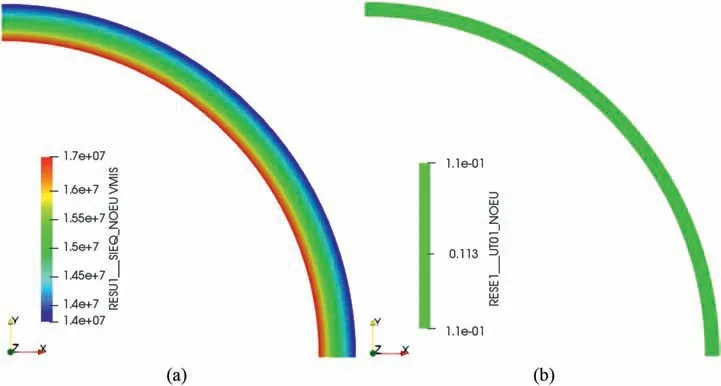
Fig. 5. (a) Equivalent stress (in Pa) in the concrete liner and (b) volumetric deformation in the outer compressible liner at 100 years.

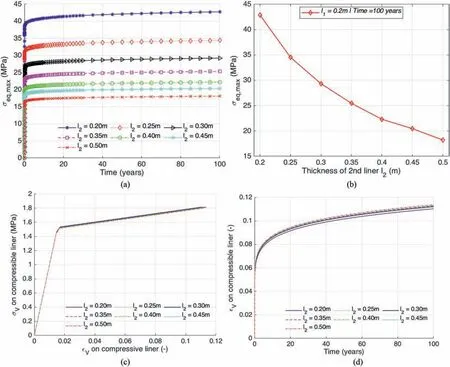
Fig.6. (a,b)Evolution of the maximum equivalent stress in the concrete liner as a function of time and its thickness;(c)Volumetric stress-strain curve in the compressible liner as a function of the concrete liner thickness;and (d) Evolution of the volumetric strain in the compressible liner as a function of time. These results are obtained by using the mean values of COx mechanical properties and the compressibility εv2 = 0.4 of the outer layer.

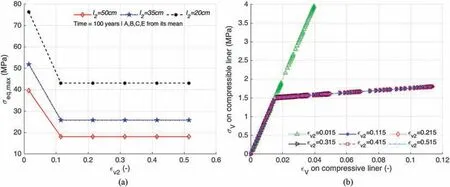
Fig.7. (a) Evolution of the maximum equivalent stress in the concrete liner as a function of its thickness and the compressible potential εv2 of the outer layer;and(b)Volumetric stress-strain curves in the compressible liner. The mean values of COx mechanical properties were used, while the thickness of the inner liner is l2 = 0.5 m in (b).

Quantitatively, the effect of each parameter of COx rock properties on the maximum equivalent stress of the concrete liner at 100 years can be evaluated by using the sensitivity analysis. The Cotter method is chosen for this purpose thanks to its applicability for the input variables regardless of their dependence.Known as an efficient and low-cost approach to the sensitivity analysis, the Cotter method allows ranking the input parameters through their indices, called Cotter indices (see Appendix B, Cotter (1979), and Homma and Saltelli(1996)for more details).As illustrated in Fig.10,the obtained results of Cotter indices show that the two coefficients A and B affect the most on the concrete liner response. While the Young’s modulus presents a moderate effect, and the influence of the coefficient C is lowest,which can be explained by its small COV among the four parameters of the COx rock.

4.2. Reliability analysis problem

The exceedance probability of the compressive stress in the concrete liner at t = 100 years with respect to an allowable value(i.e. the chosen elastic limit) is estimated in this part using the modified AK-MCS method. As discussed in a verification test in Appendix A,the convergence of probability can be attained sooner(i.e.the number of iterations at convergence is lower)if a subset of new training points is used in each iteration.Thus,in the following reliability analysis,a subset of 4 enriched samples is chosen during the iterative construction process of Kriging metamodel thanks to using the parallel calculation in Code_Aster. The initial DoE of 24 training samples of the random vector x (i.e. the mechanical properties of COx rock) is generated by the Latin hypercube sampling (LHS) method. The other necessary parameters for the modified AK-MCS reliability analysis are chosen as γ=0.01,Nγ=6,and NMCS=106,respectively.For the sake of clarity,we remind here that the parameters γ and Nγ indicate the tolerance and the number of iterations used in the stopping criterion(see Eq.(A7)in Appendix A). while NMCSdesignates the number of random samples generated for the evaluation of the failure probability through the interpolation by MCS.

Fig. 11a illustrates a representative evolution of exceedance probability of the drift’s final support during the iterative construction of the modified AK-MCS metamodel. Corresponding to the fixed values of the concrete liner’s thickness(l2=0.5 m)and the compressible potential of the compressible layer (εv2= 0.515), the convergence is obtained after 68 iterations with a total number Ncall= 296 of direct evaluations of the performance function in Code_Aster. The exceedance probability is about Pf= 0.13% in this case by adopting the allowable stress σcl= 36 MPa. This stress corresponds to the elastic limit of the concrete class C60/75 as proposed by EC2.An investigation with the smaller values of σclis also performed. As shown in Fig.11b, the result highlights an increase as expected of the exceedance probability in the concrete liner when the lower elastic threshold is chosen to limit its maximum equivalent stress. The exceedance probability at 100 years may reach about 98.51%if the threshold is reduced to 16 MPa.However, beyond the allowable stress of 25 MPa, the probability seems smaller than 1%.The numerical results also confirm that the number of direct evaluations of the performance function (Ncall) is more critical for the smaller probability.

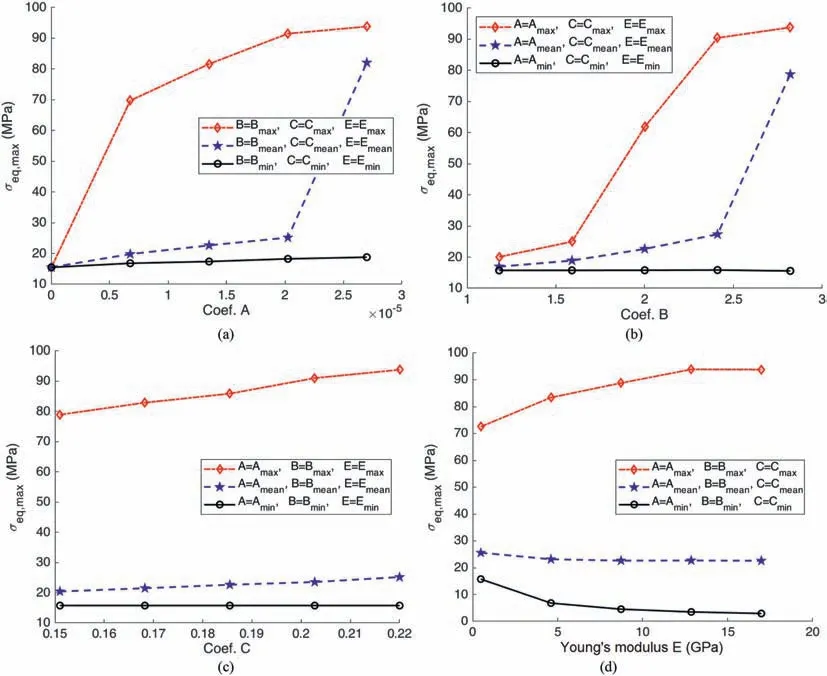
Fig. 9. Effect of each parameter of COx rock properties on the maximum equivalent stress in the concrete liner at 100 years represented by parametric studies.

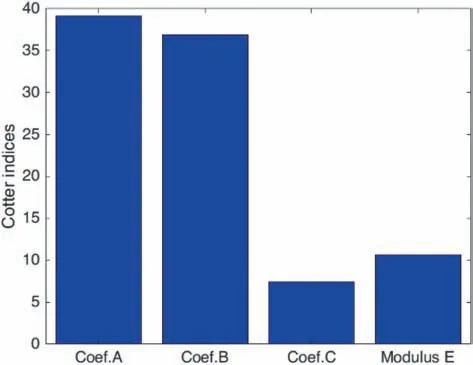
Fig.10. Effect of each parameter of COx rock properties on the maximum equivalent stress in the concrete liner at 100 years represented by the Cotter indices.

Now, by fixing the allowable stress of concrete and the compressibility of the compressible liner at σcl= 36 MPa and εv2= 0.515, respectively, we can investigate the influence of each liner’s thickness on the long-term stability of the final support of drift.We can observe in Fig.12a that the exceedance probability in this concrete support varies from 15.78% (for the case of thickness l2= 0.25 m) to 0.13% (in the case of l2= 0.5 m). The exceedance probability is smaller than 1% when the thickness of this final support is higher than 0.33 m.The result of exceedance probability in the concrete liner with the thickness of 0.5 m can increase considerably when the thickness of the outer liner decreases from 0.2 m to 0.1 m, as highlighted in Fig.12b.

Then by adopting l1=0.2 m,l2=0.5 m,and σcl=36 MPa,our last numerical investigations show that the variation of the compressibility of the outer liner can favorably affect the exceedance probability in the final support of drift (Fig.13).The long-term stability of the concrete liner is higher, representing a lower exceedance probability when the compressible potential in the first support layer increases. For the particular case of an elastic material (i.e.εv2= εv1= 0.515) characterized by only one elastic modulus(Ec= 100 MPa), the exceedance probability at 100 years of the concrete liner with 0.5 m of thickness can attain 30.96%instead of 0.13%(as in the case of εv2=0.515).This result confirms the evident effect and significant benefit of using the compressible material to ensure the stability of drift support.

5. Discussion

Based on different simplified assumptions,the study conducted in this work presented our preliminary results of the long-term stability analysis of drift. We can expect that the exceedance probability of the drift support can be higher than the ones obtained in this research when the uncertainty is quantified from the in situ data in which the spatial variability of rock properties and other mechanisms (e.g. damage,THM coupling) are considered.

Indeed, it has been shown in many geotechnical applications that the spatial variability of rock properties can contribute to the most significant source of uncertainty (Chen et al., 2019; Shokri et al., 2019; Gao et al., 2020). However, in the literature, this source has been taken into account in two different manners. The first approach consists of considering all uncertainty sources in the reliability analysis regardless of the heterogeneous distribution in the space of the random parameters.By using this approach in the case of drift,the surrounding rock mass is kept homogeneous,and the problem can be solved similarly to the ones of this work(i.e.by using the modified AK-MCS metamodel).

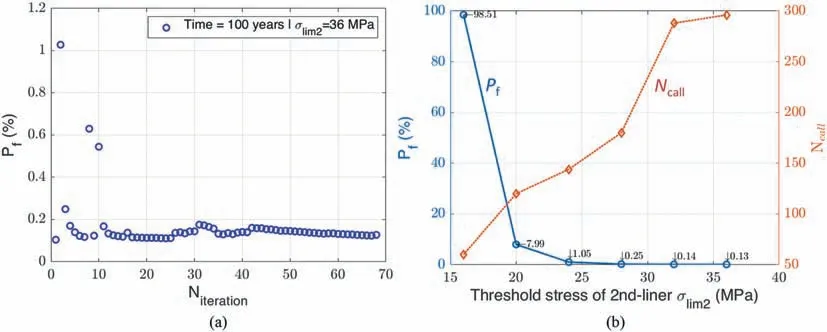
Fig.11. (a) Evolution of exceedance probability of the concrete liner at 100 years during the iterative construction of the modified AK-MCS metamodel (σcl = 36 MPa); and (b)Exceedance probability as a function of allowable stresses σcl. The fixed values of l2 = 0.5 m and εv2 = 0.515 were used.

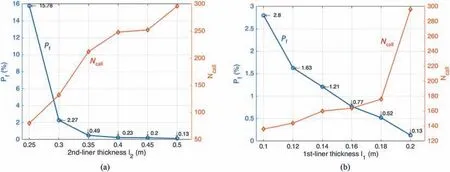
Fig.12. (a)Exceedance probability of the concrete liner at 100 years as a function of the inner liner thickness(with l1=0.2 m),and(b)of the outer liner thickness(with l2=0.5 m)using the fixed values of εv2 = 0.515 and σcl = 36 MPa.

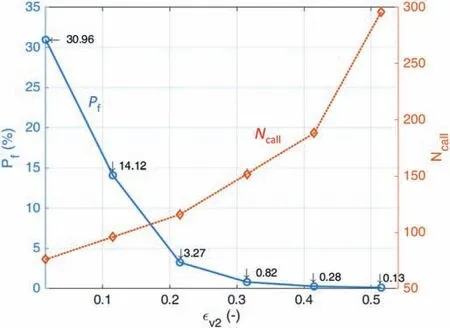
Fig. 13. Influence of the compressible potential εv2 of the compressible layer on the exceedance probability of the concrete liner at 100 years (by fixing l1 = 0.2 m,l2 = 0.5 m and σcl = 36 MPa).

The second approach aims at accounting for the spatial effect by modeling the heterogeneous medium (also known as the variability problem to distinguish the uncertainty problem in the first approach).For this purpose,the notion of a random field is usually chosen to describe the spatial distribution of a random variable.Mathematically,this random field can be expressed in the form of a correlation function (such as Markovian or Gaussian’s function)with an essential characteristic parameter, the spatial correlation length. For numerical modeling, this random field needs to be discretized, and the variability problem becomes a particular case of the uncertainty problem but with a high dimension(Tran,2020).Indeed, the dimension of the variability problem can dramatically increase when the spatial correlation length is smaller and/or the adopted geometric model of the structure is large.Correspondingly,the computational demand increases exponentially as the number of variables grows.Solving the great dimensional problem,referred to as the curse of dimensionality,is still an active ongoing research topic in the literature.The efforts of most studies are based on the idea of using the dimension reduction method to construct the appropriate surrogate. Concerning the Kriging-based metamodeling technique, some extensions have been proposed (Lelièvre,2018; Wang and Fang, 2020) to handle this problem. Although the ability of these improvements was demonstrated, notably in different academic problems, considerable limits always exist in real applications when the structure behavior is complex, and the number of random variables can range from several hundred to several thousand (Tran,2020).

By neglecting the impact of spatial distribution,the exceedance probability of underground structures provided by the first approach could be overestimated in comparison with the ones calculated by the second approach (Griffiths et al., 2009; Lü et al.,2018; Shokri et al., 2019; Tran, 2020). However, the computational demand of the first approach is significantly lower whilst the correspondingly overestimated result, represented by a higher probability,seems to be more appreciated for the stability analysis of the structure.

Besides,the estimated long-term exceedance probability of drift support in this work may be highly underestimated due to the ignorance of the damage mechanism as well as the anisotropy and the (thermo-) hydro-mechanical coupling effect. Note that the observation from the measurements at M/HM URL and from the creep tests showed a higher deformation rate linked with the damaged zone whilst anisotropy of convergences was largely observed in all drifts. The consideration of these effects (damage mechanism, anisotropy, coupling loading, and so forth) with the necessary to add the in situ data on the quantification process must contribute to another important uncertainty source of the COx properties,which may increase the risk of long-term stability the of drift’s support.

6. Conclusions

In this work, the Kriging-based reliability analysis was conducted to study the long-term stability of concrete liner of a deep drift by accounting for the uncertainty of the COx claystone. The study was undertaken in the 2D plane strain condition and under the isotropic far-field stresses to model the circular drift oriented in the major horizontal stress direction of COx formation. The timedependent mechanical behavior of this rock was assumed to be described by the classical viscoplastic model of Lemaitre. The uncertainty of the mechanical properties of COx host rock was quantified from laboratory data obtained from the triaxial creep tests. The tri-linear elastic model was proposed for the compressible liner,which was put between the concrete liner and rock mass.Based on a modification of the well-known AK-MCS method, the efficiency of the Kriging-based reliability analysis was demonstrated. The numerical results of both the deterministic problem and the reliability analysis elucidated the strong dependence of the stability of concrete liner on the uncertainty of rock properties and the compressibility of the outer compressible layer.The exceedance probability with respect to the allowable elastic limit measured at 100 years of this final support of drift decreases when its thickness increases and/or the compressible potential of the outer liner is higher. The numerical investigations confirm the tremendous benefit of compressible material on the long-term stability of drift support from a purely mechanical point of view. However, the results in this preliminary research can be underestimated when the uncertainty related to the spatial variability of COx rock properties,as well as the damage mechanism and/or the coupling effect, is neglected. The consideration of these aspects on the long-term stability analysis and optimization design of drift system support presents an essential topic for future works.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2021.06.009.