基于改进加权混合滤波的矿井RSSI定位方法

邵小强，赵 轩，聂馨超，郭德锋，郑润洋，卫晋阳

(西安科技大学 电气与控制工程学院，陕西 西安 710054)

煤矿井下人员精确定位是推进煤矿安全开采，高效生产的重要保障[1]。矿山灾难发生时，对煤矿井下工作人员的高精度定位有助于救援人员更高效开展援救工作。但传统定位技术在矿井环境中普遍存在定位精度较低、误差偏大、受环境干扰大等问题[2]。

目前，煤矿井下人员定位的方法主要有基于到达时间(TOA)、基于到达时间差(TDOA)、基于到达角度(AOA)和基于接收信号强度指示(RSSI)等[3-5]。其中，基于RSSI测距定位技术具有外设硬件少、功耗低等特点[6]，仅需要检测接收信号强度的变化来估算接收端与发射端之间的距离。但无线信号在传输过程中易受环境干扰影响，产生反射、多径效应、非视距传输等问题[7]，造成RSSI测距定位误差变大。因此，如何提高基于RSSI测距定位精度问题成为研究的热点。

文献[8]利用高斯模型对采集的RSSI值进行滤波处理，然后取均值进行测距计算，但这种算法并未考虑滤波后各信号值所占权重问题。文献[9]的处理方法是将高斯滤波后的信号值进行分组加权，但对各组权值的选取方法过于笼统，不能与各信号值对应匹配。文献[10]利用高斯滤波去除掉一些异常信号值，再用卡尔曼滤波处理RSSI数据，该算法并未考虑信号值应该随着距离的变化呈现出平滑状态。为此，笔者提出了一种基于改进加权混合滤波的矿井RSSI定位方法。

1 RSSI测距模型与误差分析

矿井定位系统通过采集井下信号节点与未知节点之间的关系，将收集到信息传输给交换机，由交换机与地面上的服务器和各管理站进行交互。常见的矿井定位系统结构如图1所示。

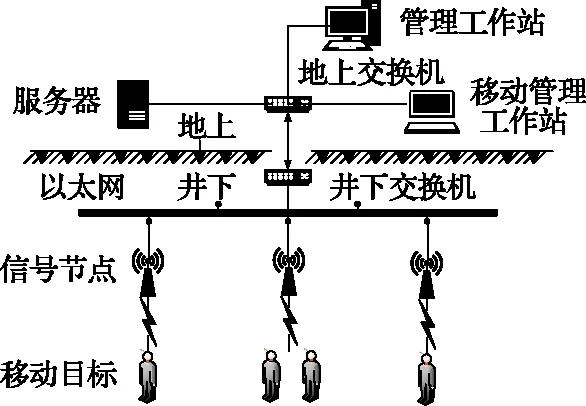
图1 矿井定位系统结构

1.1 RSSI测距模型

无线传感器网络中无线信号的传播模型主要有自由空间传播模型和对数正态阴影模型等[11]。在实际应用中一般多用对数正态阴影模型，其传播模型公式为：

(1)

式中，d为发射端与接收端之间的距离，m；d0为参考距离，通常取1m；P(d)和P(d0)分别表示距离发射端d和d0时接收的信号强度，dBm；n为路径损耗指数；Xσ是均值为0，标准差为σ的高斯随机变量，表示环境中的噪声干扰。

在实际测量中，用RSSI(d)表示P(d)，则式(1)转换为对应的RSSI值形式，其衰减模型公式[12]为：

RSSI(d)=A-10nlg(d)+Xσ

(2)

式中，A表示距离发射端1m处接收到的信号强度。由式(2)可推出距离计算公式为：

(3)

1.2 误差分析

RSSI测距主要利用发射端与接收端之间的信号强度损耗来计算二者的距离。由式(3)可知，影响RSSI测距精度的主要因素有路径损耗指数n、环境参量Xσ、以及参数A和RSSI值[13]。在RSSI测距模型应用时，人们通常给参数A和路径损耗指数n赋以经验值，并将其作为整个网络的固定模型参数，且通常不考虑环境参量Xσ的影响。但真实矿井巷道中的环境情况更为复杂，一旦环境因素发生变化，信号的传播也会受到影响，即使在相同位置不同时刻接收到的信号值也有可能产生较大的波动，影响整个系统的测距定位精度。

2 RSSI测距定位修正算法

本文提出对经过高斯滤波处理后的RSSI值进行最大值加权求解，以确定各点精确信号值，然后通过改进卡尔曼滤波器将整体RSSI值平滑输出，最后利用最小二乘法求取该环境中的路径损耗指数n和环境参量Xσ，建立修正后的RSSI测距模型进行测距定位。

2.1 RSSI值高斯滤波预处理

高斯滤波适用于服从或近似服从于对数正态分布事件的集合[14]，式(2)是一个满足对数正态分布规律的阴影传输模型，高斯滤波可以得到对测距定位参考价值更大的RSSI值。设每个未知节点接收到的n个RSSI值样本数据分别为R1，R2，…，Rn，对应的概率分别为P1，P2，…，Pn，且RSSI近似服从(μ，σ2)的高斯分布，其概率密度函数为：

(4)

式中，R为RSSI值。由极大似然估计法可求得：

(5)

(6)

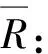
(7)

实验采集了未知节点距离信号结点30m内每间隔1m的信号值，以距离信号节点16m处采集到的信号为例，对采集到的信号值进行高斯滤波处理。高斯滤波前后的RSSI值对比效果如图2所示。可以看出，高斯滤波后可以得到一组相对稳定的信号值。

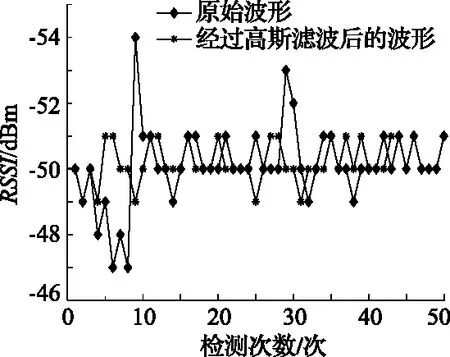
图2 高斯滤波前后RSSI值(距离16m处)

2.2 RSSI值加权处理

文献[9]指出RSSI值越大，对未知节点的参考价值就越大。因此本文在高斯滤波基础上，提出了引入最大值加权处理RSSI数据。首先找出未知节点在各位置点接收到的最大RSSI值Rmax，求出各位置点序列中RSSI值与Rmax的差为：

Di=Rmax-Ri，(i=1，2，…，n)

(8)

其中，Ri为序列中第i个RSSI值。当Ri=Rmax时，Di=0，式(8)没有意义，因此引入加权系数处理式：

(9)

归一化处理得到加权权重Wi[15]：

(10)

将序列中每个RSSI值与相对应的权重Wi相乘后累加求和得出未知节点所在位置的RSSI值。

(11)

由此可以求出个未知节点在各位置处接收到的更加精确的信号值，为提高定位精度做好铺垫。

2.3 改进卡尔曼滤波器设计

经典卡尔曼滤波算法通常采用状态空间模型来进行描述动态系统，其状态空间模型主要由状态方程和观测方程组成[16，17]，即：

Xk=Φk-1Xk-1+Wk-1

(12)

Yk=HkXk+Vk

(13)

式中，k为离散时间；Xk为系统在k-1时刻预测到的k时刻的状态信号；Yk为对应状态的观测信号；Wk-1为输入白噪声；Vk为观测噪声；Φk-1为状态转移矩阵；Hk为观测矩阵。

系统误差的协方差方程为：

(14)

式中，Pk为k时刻系统状态的协方差，Qk-1为k-1时刻系统噪声的协方差矩阵。

对式(12)中k时刻的预测状态信号和式(13)中k时刻的观测状态信号进行加权求均值，这个权值即卡尔曼增益Kk：

(15)

式中，Rk为观测噪声序列的协方差矩阵。

在k时刻Xk的最优化更新方程为：

εk=Yk-HkXk

(16)

(17)

式中，εk为测量矩阵Yk对应的新息值。

在k时刻系统误差的协方差更新方程为：

(18)

式中，I为单位矩阵。

本文卡尔曼滤波器主要用来对整体信号值进行预测更新，使整体RSSI值呈现平滑状态。经典卡尔曼滤波器是对所有位置的RSSI值进行预测、更新，而对于某些点的RSSI值在经过高斯滤波和引入最大值加权后已经达到一种理想状态，经过卡尔曼滤波后反而使其发生异变。因此，本文设计了一种改进卡尔曼滤波器对整体RSSI值进行处理。由式(16)、式(17)可知，卡尔曼滤波器主要通过新息值来影响滤波结果。因此，当信号值发生较大偏差时，应当采取一定方法来修正新息值。新息中的粗差通过增益矩阵Kk影响信号状态滤波[18]，本文提出引入等价权函数D来调整增益矩阵Kk：

(19)

则式(17)变为：

(20)

已知理想状态下，接收端接收到的RSSI值随着距离的增大而减小。假设k+1时刻RSSI值与k-1时刻RSSI值之差的绝对值为ΔRSSI，即：

ΔRSSI=|RSSIk+1-RSSIk-1|

(21)

记等价权函数D的取值为：

(22)

式中，ΔC为ΔRSSI的阈值，其取值需要根据未知节点在各位置点接收到的RSSI值来确定。本文对经过高斯加权处理后各位置点的信号值求取ΔRSSI，通过大量仿真实验得出ΔC的取值范围为1～6，在计算时取ΔRSSI的阈值ΔC=4。

2.4 最小二乘法参数拟合

根据前文介绍的RSSI测距模型及模型误差分析可知，影响RSSI测距精度的RSSI值经过高斯滤波、引入最大值加权和改进卡尔曼滤波后可以得到相对稳定的信号值，参数A即距离1m处的RSSI值，经上述处理可求得参数A=-28dBm。本文采用最小二乘法对路径损耗指数n和环境参量Xσ的值进行求解。

令RSSI值为y，x=lgd，a=-10n，b=A+Xσ，则式(2)变为y=ax+b。应用最小二乘法原理将实测值yi和计算值yj之差的平方和φ=∑(yi-yj)2最小作为“优化判据”，计算a和b。

(23)

要求的φ最小值，可用函数φ对a、b求偏导数，并令其等于零，即：

(24)

(25)

将式(24)、式(25)整理得：

(26)

(27)

求得：

(28)

(29)

由此可求出a和b的值，并可计算求出该环境下的路径损耗指数n=2.2732，环境参量Xσ=8.8212，进而建立该环境下的RSSI测距定位模型。

3 实验结果与仿真分析

参照文献[9]数据采集方法，实验环境选择西安科技大学国家重点实验室——煤炭主体专业综合实验中心。实验时不排除巷道中固定障碍物及偶尔过往行人的干扰，使实验环境更加符合真实巷道。本文只针对未知节点周围的一个信号节点进行研究，将2.4GHz频段的无线路由器固定好作为信号节点(发射端)，利用联想笔记本(网卡Inter(R Wireless-N 7260)作为未知节点(接收端)。电脑中下载WirelessMon软件进行信号采集。设置采样速率设置为7s，延迟10ms，每间隔1m测量7min，每组采集多于50个数据，共采集30组数据。

为检测本文所提方法的定位效果，将本文所提方法与文献[9]所提测距方法、均值RSSI测距和经典卡尔曼滤波估计方法进行对比。实验数据见表1，各种方法估计距离曲线和误差曲线分别如图3、图4所示。

图3 不同方法估计距离曲线

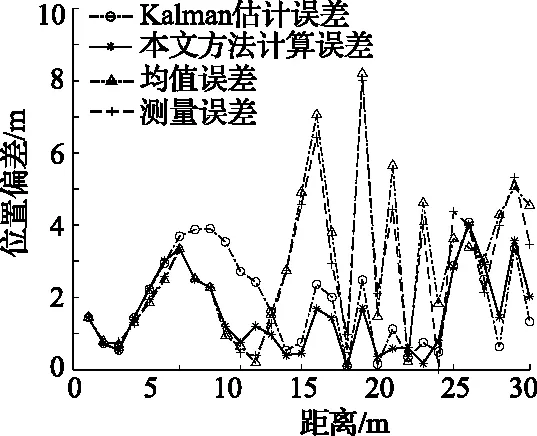
图4 不同方法估计距离误差

由表1和图3、4可知，采用本文方法所测平均误差相比于前三种方法分别降低了1.27m，1.11m和0.34m。从而证明本文所提方法的有效性和先进性。

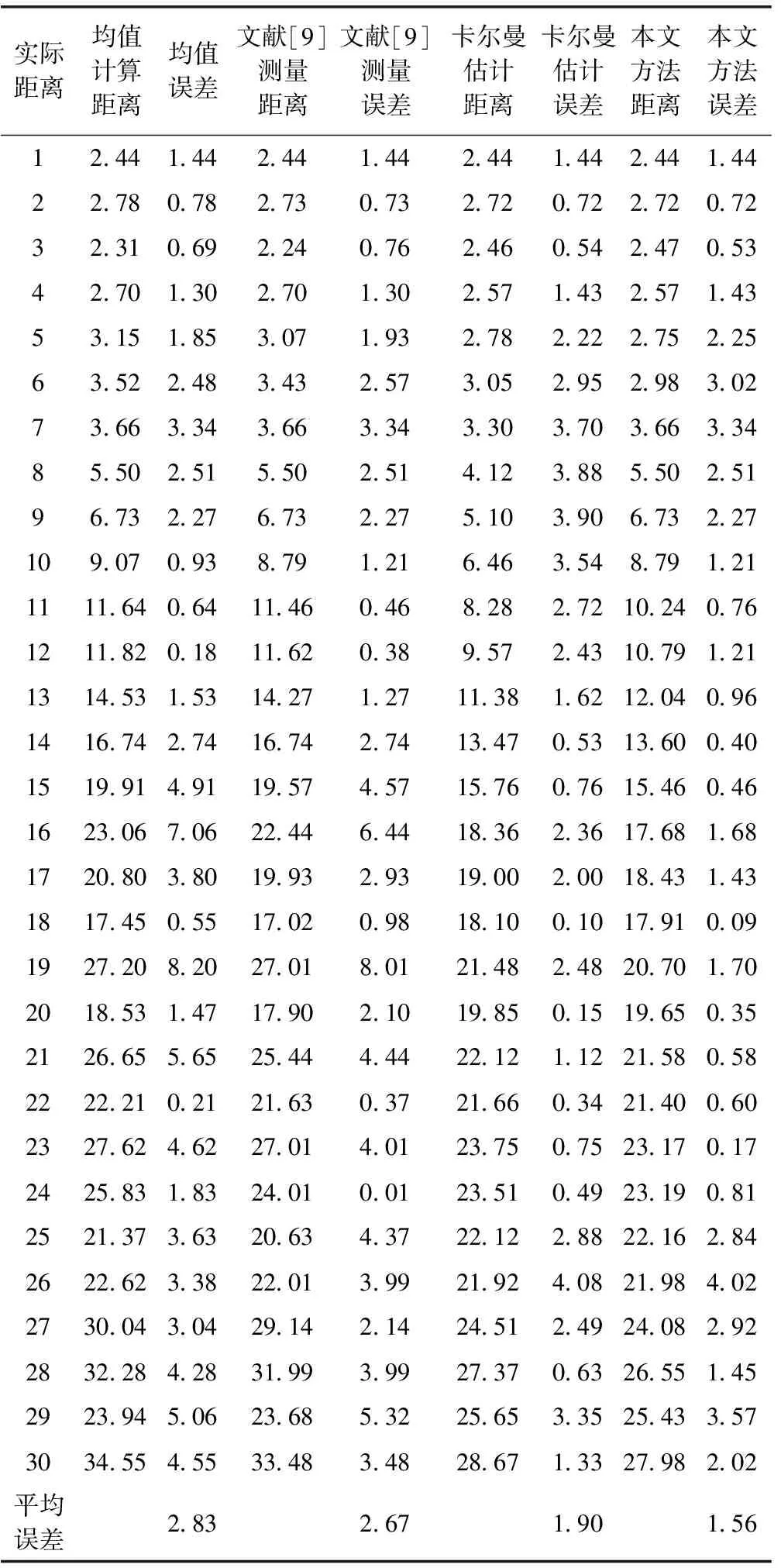
表1 各种定位方法实验数据 m

除此之外，本文对ΔC取不同值时所测距离误差进行仿真实验，仿真结果如图5和图6所示，结果见表2。

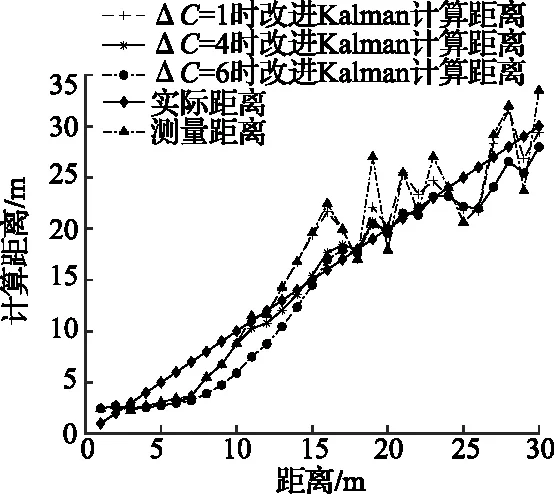
图5 不同阈值ΔC测距曲线

图6 不同阈值ΔC测距误差曲线

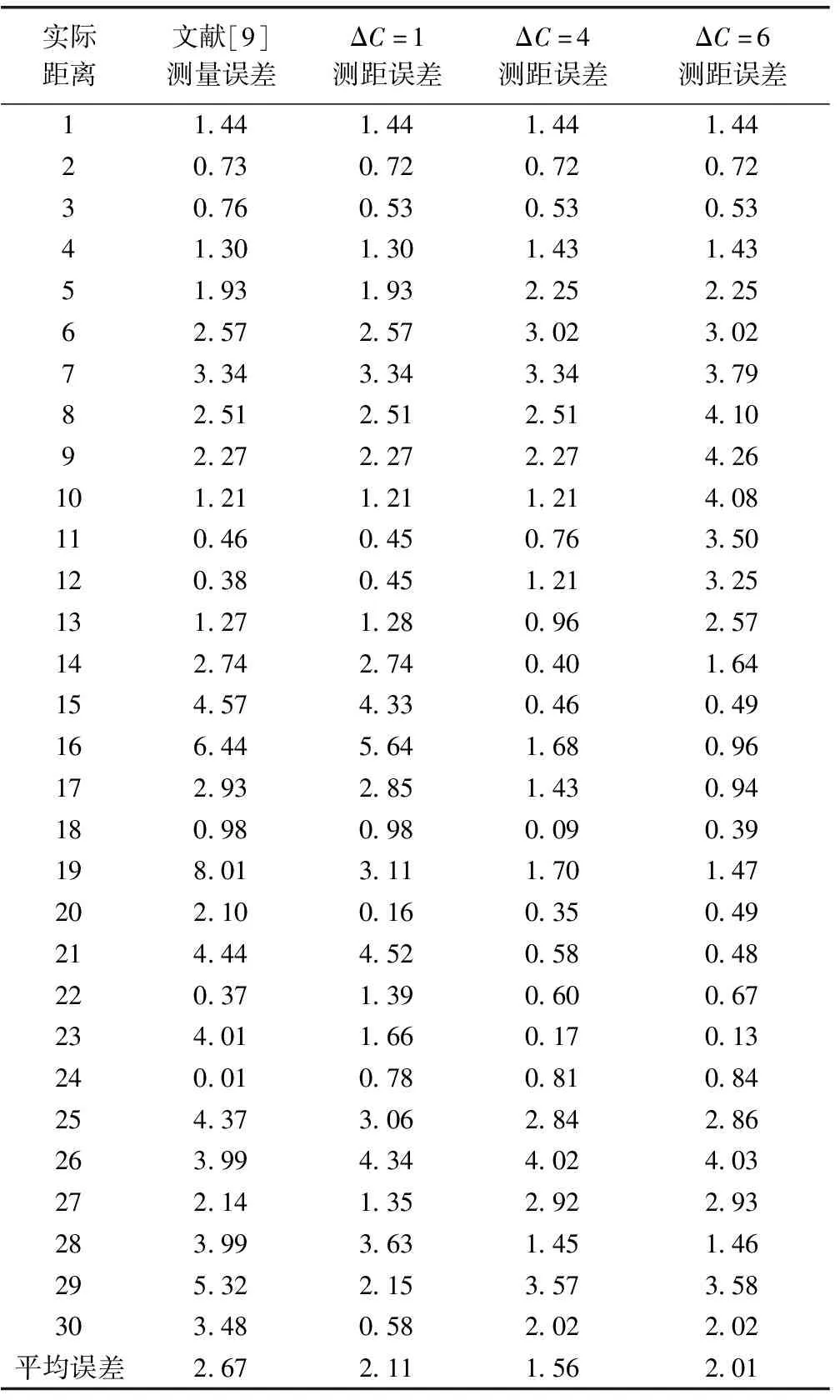
表2 不同阈值ΔC测距误差数据 m

由表2和图5、图6可知，当ΔC取值过小时改进卡尔曼滤波器达不到滤波效果，数据偏差依然较大；当ΔC取值过大又会导致改进卡尔曼滤波器将一些已经达到理想状态的信号加以修改，影响测距精度。经过大量实验仿真验证当ΔC=4时，测距曲线最接近真实距离曲线，误差曲线也明显低于其它情况的误差曲线。应用RSSI测距环境不同，阈值ΔC的取值也不同，具体取值要根据实际环境中测得的整体RSSI值来决定。

4 结 语

本文提出引入最大值加权方法对高斯滤波预处理后的RSSI值进行计算，为不同的RSSI值分配不同的权重，可以获取各位置处接收到更精确的RSSI值，避免笼统分组加权问题的出现。其次，在卡尔曼滤波器中引入阈值ΔC，通过为ΔC赋予不同的值可以有效避免传统卡尔曼滤波器盲目处理信号值的问题。最后利用最小二乘法求出特定环境下的路径损耗指数n和环境参量Xσ，打破传统为其赋以固定值或经验值的束缚，建立了符合特定巷道环境的测距模型，可以有效提升测距精度。实验仿真结果得出，在合理选择阈值ΔC的基础上，本文所提方法能够有效降低RSSI测距定位误差，定位结果也明显优于其他几种方法，为实现RSSI测距定位方法在煤矿井下的有效应用提供了可能。