基于常态挖掘路径的液压挖掘机轨迹规划方法

冯明豪，任志贵,2，魏万行，孙浩然，李佳豪

1陕西理工大学机械工程学院 陕西汉中 723000

2陕西省工业自动化重点实验室 陕西汉中 723000

液压挖掘机器人可以独立工作，也可以远程控制，已成未来挖掘机发展的重要方向之一[1]。轨迹规划在挖掘机器人的控制中有非常重要的作用，直接影响挖掘机器人作业的运动平稳性和准确性[2]。挖掘机器人的操作过程就是通过轨迹规划，将挖掘机的作业任务变成期望的运动和力，由底层控制环节生成相应的信号，产生相应的控制，使挖掘机器人输出实际的运动和力，从而完成预期的作业任务[3]。一般来说，如果在没有任何约束条件下，挖掘机器人的铲斗齿尖作业起始点到终止点的轨迹有无数条，根据是否采用最优化方法进行最优轨迹寻找，可将轨迹规划分为一般轨迹规划和最优轨迹规划[4]。李海虹等人[5]分别采用n次多项式法、傅里叶级数拟合法、分段多项式插值法对一条 T 型路径进行一般轨迹规划，对规划前后的动力学特性进行对比评价，得出函数拟合法的轨迹规划结果更平稳连续、振动强度更低的结论。潘双夏等人[6]采用最优轨迹规划方法优化了速度梯度和液压缸的总移动距离，使得挖掘机的规划轨迹更加稳定和节能，但轨迹规划只应用在挖掘机修整平面作业的路径上，其路径实际上是一条直线。目前，对液压挖掘机器人轨迹规划的研究多数停留在简单路径，如直线、圆弧等[7]，未考虑应用在复杂路径上，且挖掘工况主要集中在各液压缸单独挖掘的作业形式，复合挖掘的作业形式较少[8]。

笔者以减少液压缸长度变化量作为优化目标，运用粒子群优化算法对一条真实复合挖掘路径进行轨迹规划，更符合挖掘机真实作业情况，同时达到减少挖掘机器人能耗的目的。

1 液压挖掘机轨迹规划流程

根据液压挖掘机器人的结构，工作装置可以简要描述为位姿空间 [x，y，z，ξ]T、关节空间 [θ0，θ1，θ2，θ3]T和驱动空间 [θ0，λ1，λ2，λ3]T[9]。工作装置连杆坐标系如图 1 所示，ξ为姿态角，是水平方向与铲斗齿尖和铲斗铰点连线之间的夹角[10]。

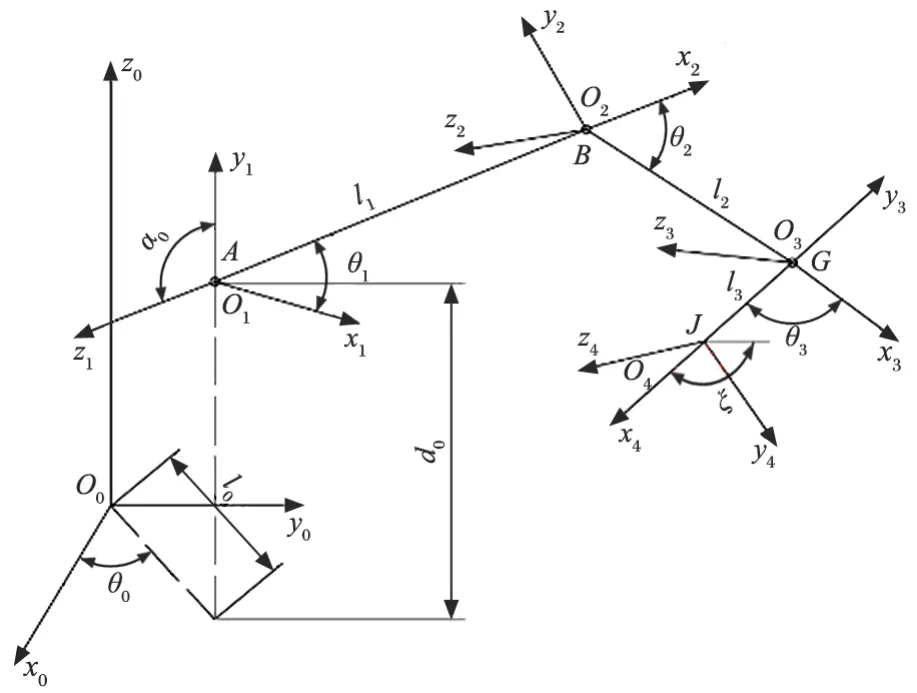
图1 工作装置连杆坐标系Fig.1 Coordinate system of linkage of working unit

基于机器人学，常用的液压挖掘机轨迹规划流程先规划关节转角，然后进行关节空间变量和位姿空间变量的相互转换，使铲斗齿尖达到预定的运动。而挖掘机在实际作业时，由于和工业机械手的作业对象不同，对姿态角的限制更为严格[11]。因此，笔者将以姿态角ξ作为控制变量，通过优化方法计算姿态角ξ，减少 2 个相邻位姿之间的液压缸长度变化量。

在确定预设路径之后，对路径上的点进行等步长分割离散化，确定每个离散点的 [x，y，z]T值。通过优化方法计算各离散点对应的姿态角ξ，确定位姿空间离散点坐标的 [x，y，z，ξ]T值后，由式 (1) 解出各离散点的关节空间坐标：

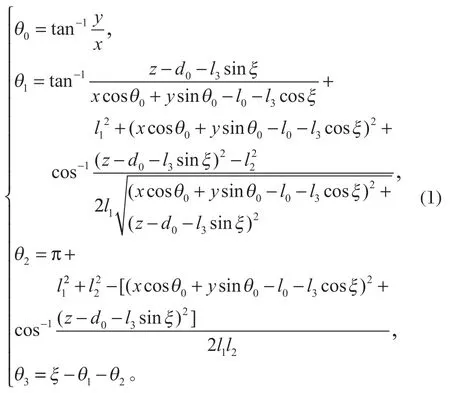
式中：θ1为zi-1轴从xi-1轴到xi轴的旋转角度，规定逆时针方向为正；αi为xi轴从zi-1轴到zi轴的转角，规定逆时针方向为正；li为连杆i的长度；di为xi-1轴与xi轴沿zi-1轴的垂直距离；i为连杆数量。

液压挖掘机工作装置机构简图如图 2 所示。根据得到的各离散点关节空间坐标 [θ0，θ1，θ2，θ3]T值设定作业时间后，可以通过多项式插值方法完成轨迹规划。基于各离散点的关节空间坐标值，还可以根据挖掘机的几何结构，由式 (2)[12]计算出各离散点的驱动空间坐标 [θ0，λ1，λ2，λ3]T值：

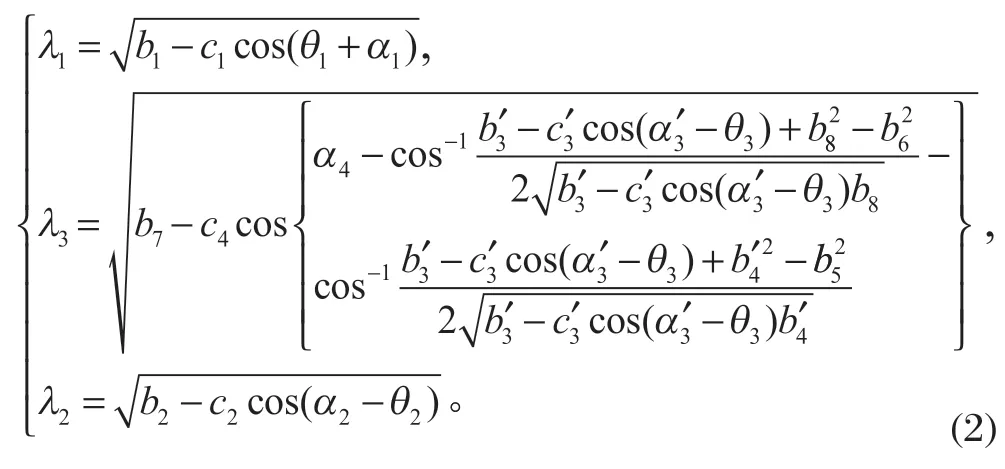
其中α1=∠BAC+∠FAx1，b1=AC2+AF2，c1=2AC·AF，如图 2(a) 所示；

α2=π -∠GBH+∠ABD，b2=BD2+BH2，c2=2BD·BH，如图 2(b) 所示；

α3′=π -∠JGL+∠BGN，b3′=GN2+GL2，α4=∠GNE，b4′=NG，b5=GL，如图 2(c) 所示。

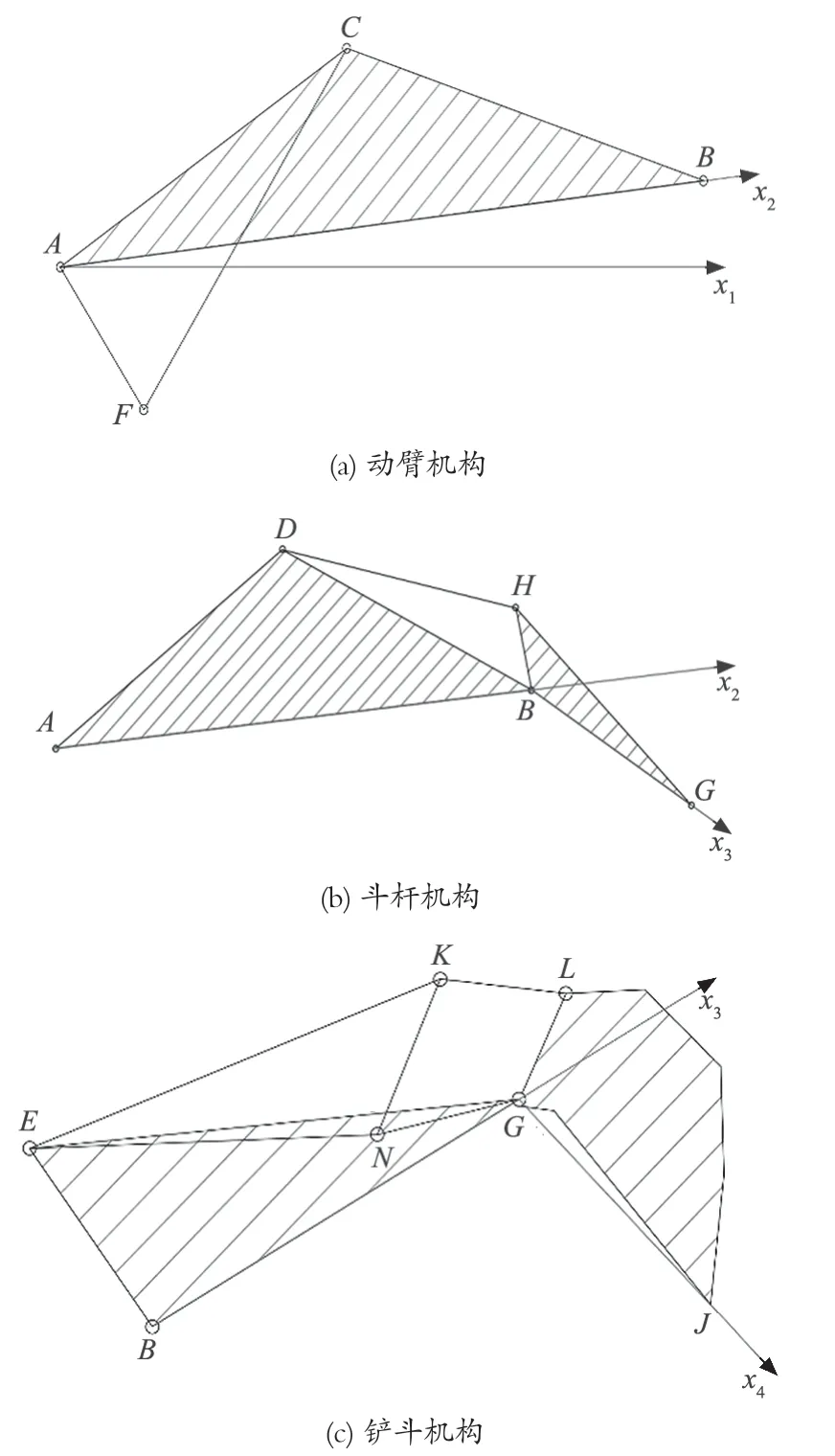
图2 液压挖掘机工作装置机构简图Fig.2 Mechanism sketch of working unit of hydraulic excavator

2 轨迹规划数学模型

2.1 目标函数

为了提高液压挖掘机作业平稳性，降低能耗，将动臂机构、斗杆机构和铲斗机构的相邻位姿之间液压缸长度变化量最小化作为优化目标。子目标函数如下：

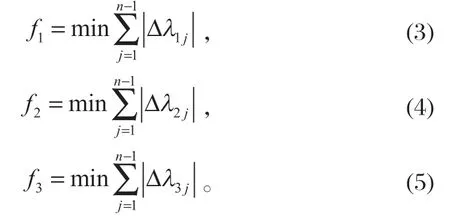
式中：n为轨迹曲线取点的数量。

根据挖掘机各工作装置液压缸长度变化范围对挖掘机所有液压缸长度之和的影响，经过无量纲处理后采用权系数法，对各子目标加上η1、η2和η3作为权重因子，满足η1+η2+η3=1，将 3 个子目标函数集合为一个通用目标函数：

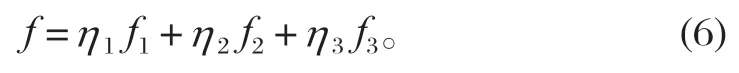
2.2 设计变量

将每一个离散点所对应的姿态角ξi(i=1～n) 作为优化的设计变量。

2.3 约束条件

(1) 关节转角约束 动臂、斗杆、铲斗关节转角不应超过各部分转角限制。

(2) 液压缸长度约束 动臂、斗杆、铲斗液压缸长度不应超过各部分液压缸长度限制。

(3) 姿态角约束 在挖掘机工作范围内，当铲斗齿尖的空间位置确定时，其姿态角不可能为 360°范围内的任意角，那么铲斗齿尖所在的位置相对于其不能实现的姿态角范围是盲位，这一不能实现的姿态成为该位置的盲角。由于盲位与盲角的存在，导致挖掘机铲斗位于某个位置时，往往不能实现特定的姿态；反之，当铲斗处于某种姿态时不能到达所要求的位置，这意味着挖掘机在作业过程中，可能不能同时完成任意位置和姿态的要求。在某一点位姿空间坐标 [x，y，z]T值给定的情况下，姿态角允许的范围为 (ξ0，ξf)，任意点姿态角范围的计算[13]如下：当θ1=θ1max，或θ2=θ2min、θ3=θ3max时，会出现ξ0；当θ1=θ1min、θ2=θ2max，或θ3=θ3min时，会出现ξf。

3 不同规划方法的对比分析

由于在真实复合挖掘路径上验证各方法的节能效果比较困难，而 T 型路径由D1～D6这 6 个点连成的直线组成，计算相对简单，遂选用 T 型路径进行验证。以某 8.5 t 挖掘机在一条 T 型路径 (见图 3) 上作业为例，对 3 种规划方法进行对比分析，再选择节能效果最好的方法对真实复合挖掘路径进行轨迹规划。

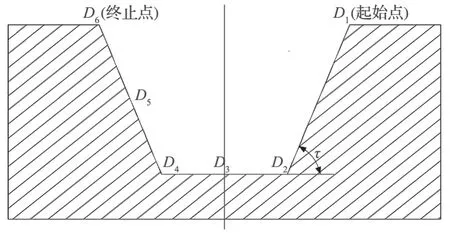
图3 T 型路径Fig.3 T-shaped path

3.1 经验法

在挖掘机轨迹规划的经验法中[14]，将切削后角β设为定值，当后角出现盲角时，调整后角消盲。通过下式计算出每一点的姿态角：

式中：τ为路径上某一点与x轴正方向的夹角，如图4 所示。

再依据已知的 T 型路径上各点的 [x，y，z]T值，根据第 1 节中的轨迹规划流程得出液压缸长度变化的计算结果，如图 4 所示。

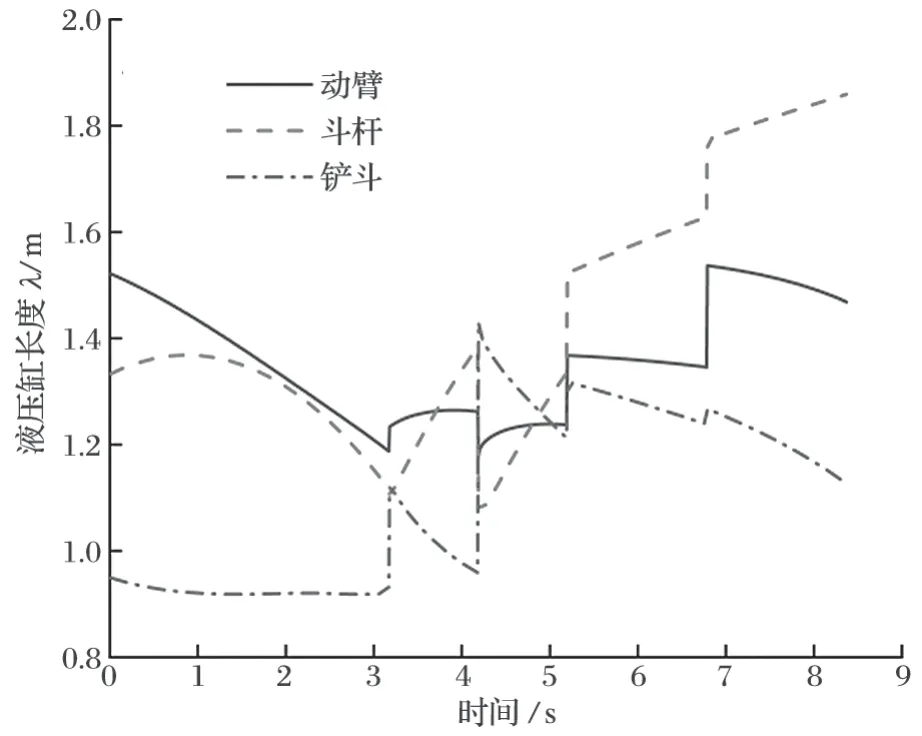
图4 采用经验法得到的液压缸长度变化曲线Fig.4 Variation curves of length of hydraulic cylinders obtained with empirical method

3.2 MATLAB 优化工具箱

将第 2 节所提到的目标函数、设计变量和约束条件输入 MATLAB 优化工具箱，采用其中的 fmincon函数，以经验法的各离散点的姿态角值作为初始值，得出优化后各离散点的姿态角值，并根据第 1 节中的轨迹规划流程得出液压缸长度变化的计算结果，如图5 中的 3 条实线曲线 (O 组曲线) 所示。相比于图 4 中经验法的规划效果，采用 MATLAB 优化工具箱后的液压缸变向点明显减少，即由于液压缸阀门频繁换向所产生的振动有所减小。

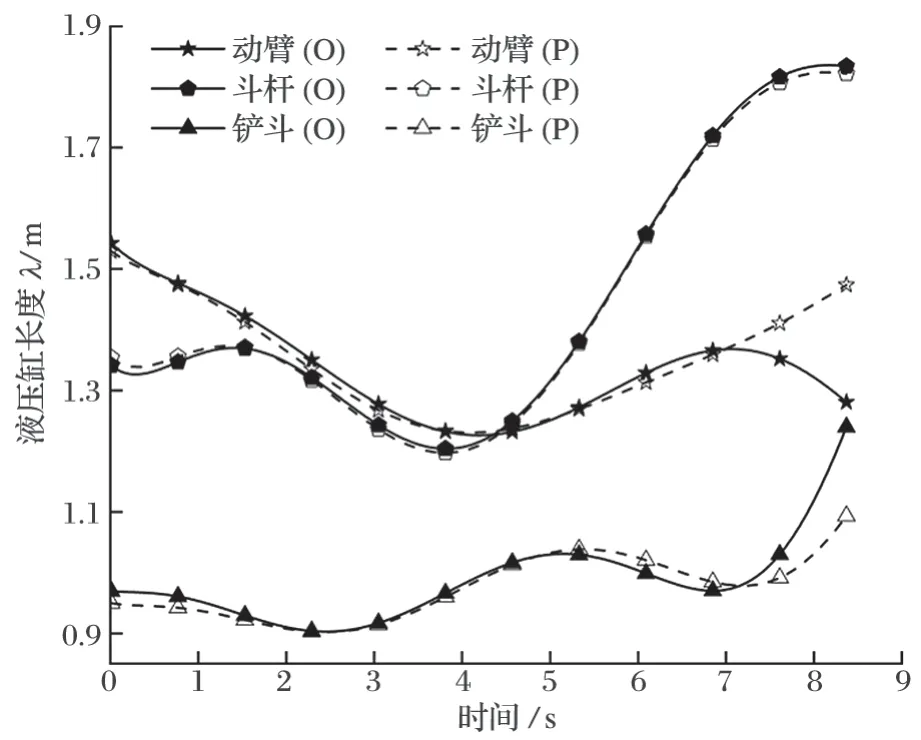
图5 采用 MATLAB 优化工具箱和粒子群优化算法得出的液压缸长度变化对比Fig.5 Comparison of length variation of hydraulic cylinders obtained with MATLAB optimization toolbox and PSO algorithm

3.3 粒子群优化算法

采用粒子群优化算法进行轨迹规划，设置粒子群数量为 1 500 个，粒子维数为每段直线离散点数量，最大迭代数为 200，惯性权重为 0.5，学习因子c1、c2均为 2，得到优化后的各离散点的姿态角值，同样根据第 1 节中的轨迹规划流程得出液压缸长度变化的计算结果，如图 5 中 3 条虚线曲线 (P 组曲线) 所示。相比于图 4 中经验法的规划效果，采用粒子群优化算法得到的液压缸变向点数量明显减少，且相较于采用MATLAB 优化工具箱的变向点数量更少，因而粒子群优化算法比 MATLAB 优化工具箱法的规划效果更好。在接近时间末端时，采用粒子群优化算法得到的液压缸长度变化曲线更平滑，突变更小。采用 2 种优化方法相对于经验法的改进效率如表 1 所列 (其中x为第2.1 节中目标函数的计算结果，即液压缸最小长度变化量，表 3 同)。从表 1 可以看出，采用粒子群优化算法得到的总液压缸长度变化量更少，能耗更低，优化效果更好。

表1 采用 MATLAB 优化工具箱和粒子群优化算法相对于经验法的改进效果对比Tab.1 Improvement effects of MATLBA optimization toolbox and PSO algorithm compared with expirical method

4 基于常态挖掘路径的轨迹规划

4.1 常态挖掘路径选取

测试机型为某 36 t 的反铲液压挖掘机，基本参数如表 2 所列。测试地点为湖州某试验场，挖掘对象为混有石块的Ⅲ级土壤，作业现场如图 6 所示。采用倾角传感器对挖掘机各关节角位移进行测量[15]，取停机面最大半径挖掘工况作为本次轨迹规划路径。由于受到客观条件的限制，直接对此路径进行连续轨迹规划比较困难，取路径拟合结果所得路径方程进行轨迹规划，结果如图 7 所示。

图6 作业现场Fig.6 Operation scene

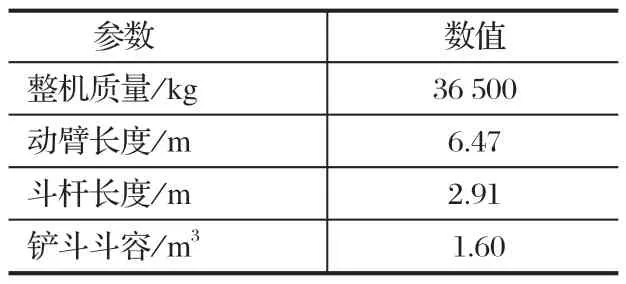
表2 测试机型基本参数Tab.2 Basic parameters of test excavator

4.2 停机面最大半径挖掘路径轨迹规划

选择粒子群优化算法按照第 1 节中的轨迹规划流程进行轨迹规划，结果如图 8 中 A 组 3 条虚线曲线所示。将其与试验得到的液压缸长度变化曲线 (B 组 3条实线曲线) 进行对比可知，两者除动臂液压缸长度变化接近外，采用粒子群优化算法得到的液压缸变向点数量减少，液压缸长度变化时过渡更加平滑。采用粒子群优化算法相对于试验结果的改进效果如表 3 所列。

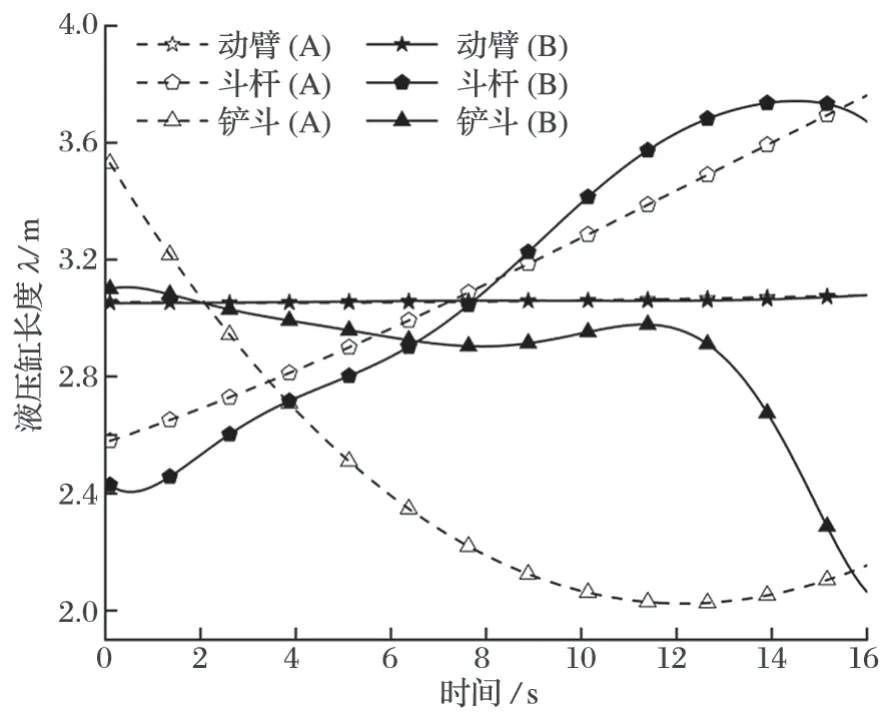
图8 采用粒子群优化算法与试验得到的液压缸长度变化对比Fig.8 Comparison of length variation of hydraulic cylinders obtained with PSO algorithm and test

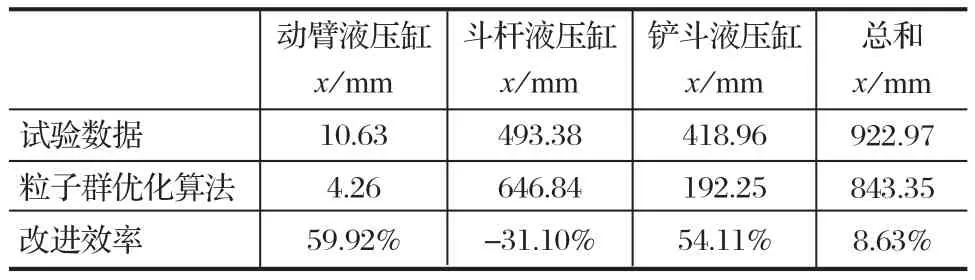
表3 采用粒子群优化算法相对于试验结果的改进效果Tab.3 Improvement effects of PSO algorithm compared with test data

由于对各关节在中间点时的速度有约束，所以采用 4-3-3-……-3-3-4 多项式插值方法[16]得到的轨迹规划结果如图 9～ 11 所示。由图 9～ 11 可知：各关节角位移、角速度变化曲线平滑连续，角加速度变化曲线连续，保证了各关节角变化平稳连续；起始点、终止点速度、加速度均为零，能够完成连续路径下的全过程工作，满足挖掘机挖掘过程中的性能要求。

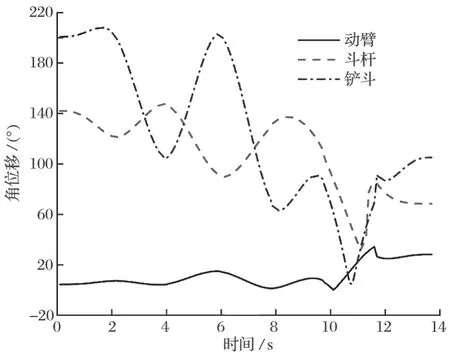
图9 角位移变化曲线Fig.9 Variation curves of angular displacement

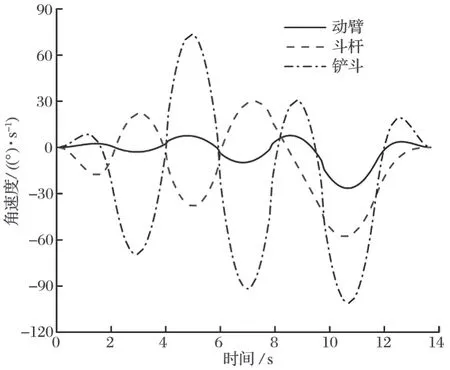
图10 角速度变化曲线Fig.10 Variation curves of angular velocity

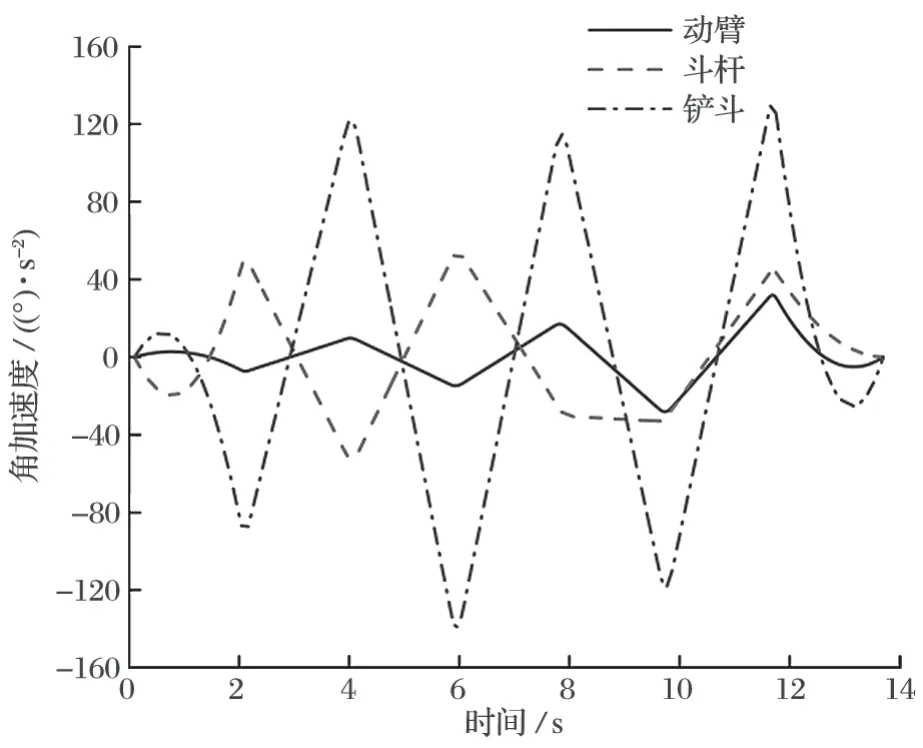
图11 角加速度变化曲线Fig.11 Variation curves of angular acceleration

5 结语

在分析液压挖掘机工作机理及运动学建模基础上，通过对 3 种方法的比较，以挖掘机器人工作平稳性和节能作为重点，选择采用粒子群优化算法对挖掘机器人运动轨迹进行规划，在一条实际复合挖掘路径上加以验证，并与试验数据进行对比，得出该方法效果良好的结论。对于复合挖掘来说，笔者对挖掘机器人动力学部分涉及不够，针对这点，会在后续研究中进一步深入。