提升机盘式制动器碟簧刚度测量与预测研究

胡成名

中煤科工集团武汉设计研究院有限公司 湖北武汉 430064

施加于提升机制动盘上的正压力是依靠碟形弹簧储积的压力能产生的。碟形弹簧在频繁使用中，由于金属的疲劳现象引起其刚度下降，若刚度急剧下降，则制动正压力下降，制动过程越来越慢，进而导致制动失效；这将造成严重后果[1]。碟形弹簧的刚度是影响制动系统能否正常工作的重要因素，对其刚度的测量和预测研究有着重要的意义。

近年来，国内学者对碟簧的变形、疲劳寿命以及刚度都有不同的研究。张媛等人[2]利用 ANSYS 仿真软件建立碟簧的有限元模型，进行疲劳分析，并预测其疲劳寿命。米月花等人[3]的研究表明，碟簧是物理非线性弹簧，载荷与变形呈非线性关系。王晓波等人[4]用LS-DYNA 有限元软件对碟簧进行数值模拟，得到载荷和变形的关系曲线。上述研究大都基于软件模拟，而没有依据生产中的实测数据。笔者提出一种测量蝶簧刚度的方法，并依据实测数据对碟簧刚度进行有效预测。

1 碟簧刚度的测量方法

盘式制动器的力学模型[5]如图 1 所示。

图1 盘式制动器力学模型Fig.1 Mechanical model of disk brake

当液压站油压p(t) 为系统最高油压时，制动器处于完全开闸状态，盘式制动器的速度为 0，此时

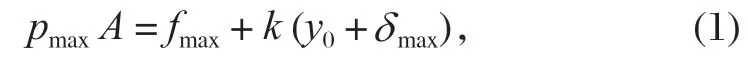
式中：pmax为液压站最高油压，MPa；A为液压缸有效作用面积，mm2；fmax为液压缸壁的摩擦阻力，N；k为碟簧的刚性系数，N/m；y0为碟簧的预压缩量，mm；δmax为开闸时的闸瓦间隙，mm。

当制动器制动时，油压p(t) 减小。盘式制动器运行δmax后，闸瓦刚刚贴上制动盘时，此时的油压即为贴闸油压pt，则有

贴闸后，油压p(t) 继续减小至系统残压pc时，制动力最大为Nmax，则有

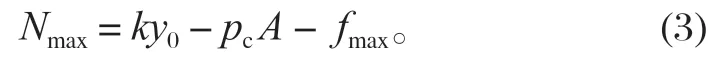
当制动器解除制动时，油压p(t) 增大。当闸瓦刚刚离开制动盘时，碟簧的压缩量为y0，此时的油压即为开闸油压pk，则有

联立式 (1) 和式 (4) 可得

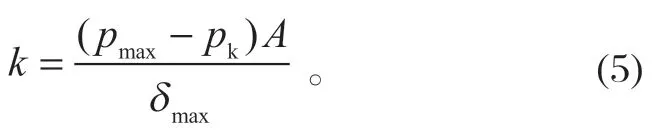
式(5) 表示了碟簧刚度的大小可以通过测得闸瓦的最大油压pmax、开闸油压pk和闸瓦间隙δmax来间接求得。

获取开贴闸油压的步骤如下：

(1) 将提升容器停在井筒中交锋位置，然后锁住滚筒；

(2) 在提升机闸瓦全制动状态下，利用位移传感器测出各闸的位移值，并在软件中以一维数组存储；

(3) 在闸瓦制动状态下，缓慢扳动手柄，使油压从残压缓慢上升到最大油压，然后再使油压从最大油压缓慢下降，同时记录各闸的位移变化和油压变化，并与步骤 (2) 测出的各闸贴闸时的位移进行比较，求得开闸点和贴闸点的油压。

图2 所示为一次测量的数据曲线。

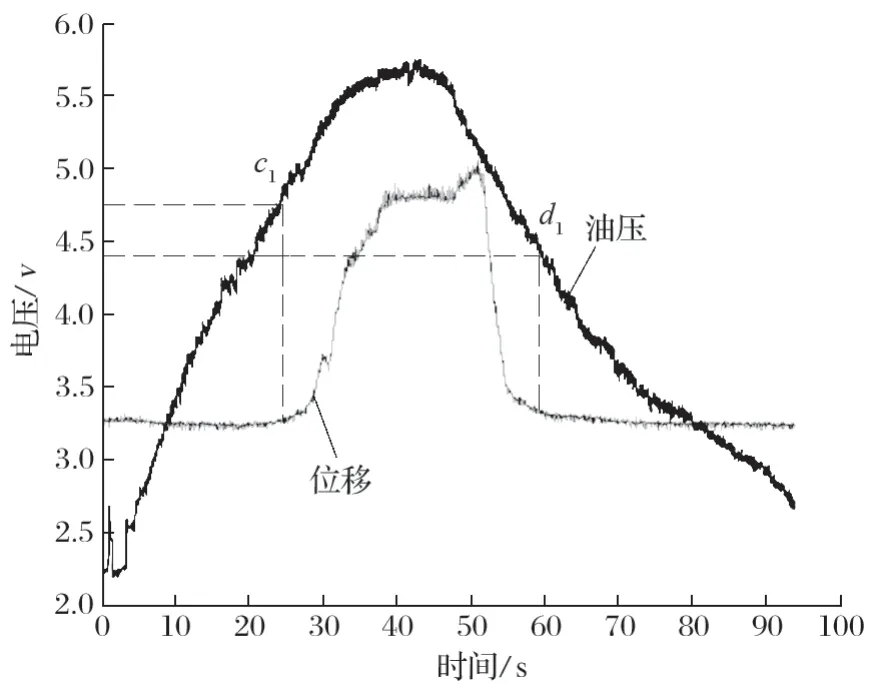
图2 现场测试的位移与油压曲线Fig.2 Variation curve of displacement and oil pressure in field test

由图 2 可知：从残压上升到最大油压用时 45 s，从最大油压下降为残压用时 50 s，整个过程用时 95 s；该闸瓦的贴闸点和开闸点都比较明确，开闸点c1与贴闸点d1所对应的压力传感器的电压输出值分别为4.75 V 和 4.4 V。根据电压与油压的线性关系可知，两点对应的油压分别为 3.437 5 MPa 和 3 MPa。

利用闸瓦的最大油压、开闸油压和闸瓦间隙间接求得碟簧刚度的方法，对龙东煤矿副井某一碟簧刚度进行连续 6 个月测值，结果如表 1 所列。

表1 碟簧刚度Tab.1 Stiffness of disk spring ×105 N/m

间接法求得盘式制动器碟簧刚度，需要在停机状态下进行，这影响了矿山企业的正常生产，由此可见，碟簧刚度预测的必要性。

2 GM(1,1) 建模方法

盘式制动器碟簧刚度的变化是一个缓慢的过程，也是一个非平稳的过程，难以用某一传递函数表示，可以认为其是一个灰色系统[6]。灰色系统过去和现在的信息综合反映了诸多因素的综合作用，包含着系统未来发展信息，可以用系统过去和现在的信息对未来进行预测；因此碟簧刚度未来随时间的变化也可以用过去和现在的信息进行预测[7]。碟簧刚度是随时间变化的序列值，笔者采用目前应用最为广泛的数列预测模型 GM(1,1) 对碟簧刚度进行预测[8]。GM(1,1) 主要适用于等时间隔的离散数据的灰色建模，对于非等时间隔数据，可通过数学变换 (拉格朗日插值法、样条插值法) 形成等间隔数据。其建模步骤如下。

2.1 累加生成碟簧刚度新数据列

设时间序列x(0)有n个观察值，

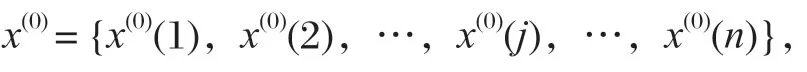
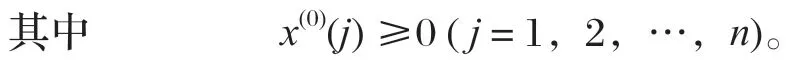
通常碟簧刚度的原始数据呈现离乱现象，灰色理论将无规律的原始数据累加生成，使其变为较有规律的生成序列。新序列用x(1)表示，

2.2 建立微分方程

建立白化形式的微分方程 GM(1,1)，

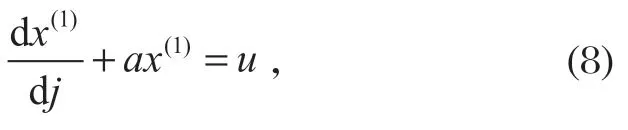
式中：a为发展灰数；u为内生控制灰数。

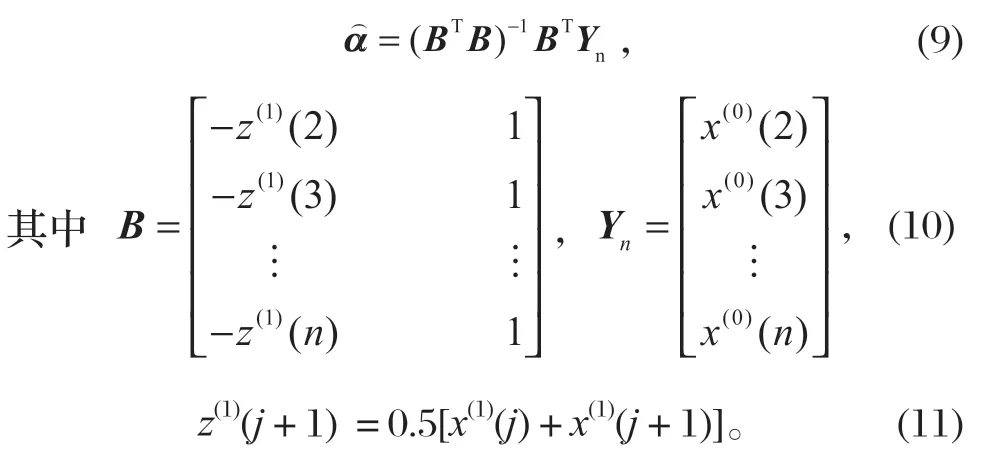
2.3 获得预测模型

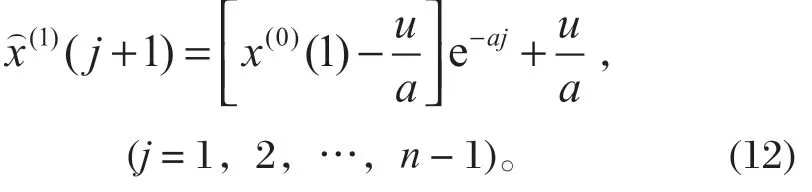
因灰色数列模型实际上是生成序列模型，对累加生成数据必须经过逆生成-累减还原后才能使用。进行累加生成的逆运算，还原预测数据列：

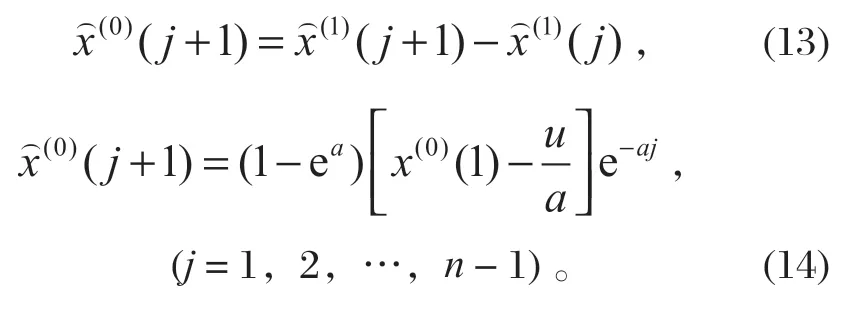
3 预测模型精度检验

在建立了碟簧刚度的预测模型后，需要对预测模型进行效果分析，检验和判断预测模型的精度。

后验差检验考虑了原始数据列的离散性，也考虑了拟合残差离散性，同时小概率实践考虑了拟合优度，因此笔者采用后验差检验的方法对碟簧刚度的预测模型进行精度分析。

后验差比值C与小误差频率P是后验差检验的两个重要指标，其中

式中：S2为残差样本的q(j) 的标准偏差；S1为实际数据样本x(0)(j) 的标准偏差。

式中：x(mean) 为数据样本x(0)(j) 的平均值。

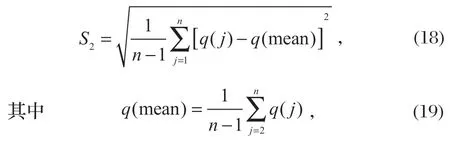
式中：q(mean) 为残差样本q(j) 的平均值。

小误差频率P的表达式为

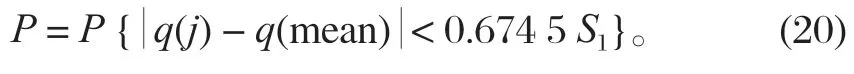
作为一个综合指标，C越小越好，P越大越好。C小表明，尽管原始数据很离散，但模型所得计算值与实际值之差并不太离散[9]，一般要求C＜ 0.35。P大说明，残差与残差样本平均值之差小于给定值 0.674 5S1的点较多，一般要求P＞ 0.95。按P和C的值综合评判模型的精度，具体指标如表 2 所列。

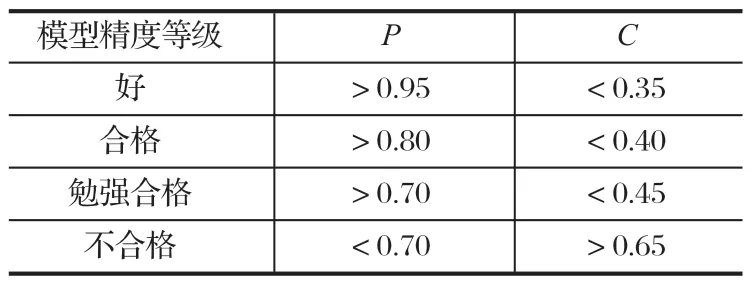
表2 模型精度等级指标Tab.2 Class indexes of model precision

4 碟簧刚度预测实例

采用 GM(1,1) 模型对龙东煤矿副井提升机制动系统碟簧刚度进行预测分析。

4.1 获得预测模型

用x(0)表示碟簧刚度原始数据序列值，如表 1 所列。根据式 (7) 计算累加值，得到新序列x(1)，如表 3所列。

表3 数据列Tab.3 data sequence ×105 N/m

根据式 (11)，得到z(1)=(8.095，13.440，18.730，24.007 5，29.279)。

根据式 (10)，求得数据矩阵B、Yn：

将B和Yn代入式 (9)，得参数向量

故a=0.005 1，u=5.397 8。

微分方程为

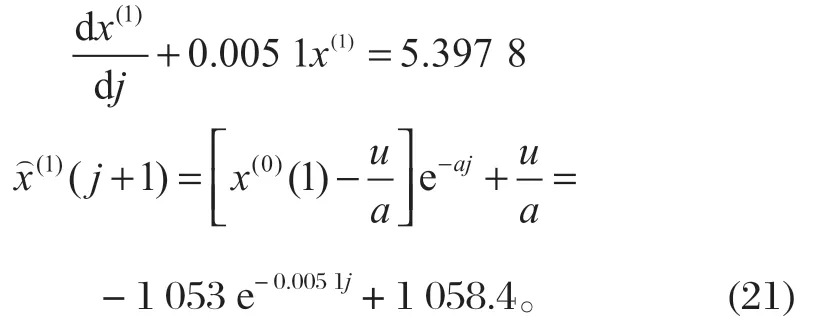
由式 (13) 求得^x(1)(j+1) 模型的计算值^x(1)与实际值x(1)，以检验模型精度，结果如表 4 所列。j=0，1，2，3，4，5。

表4 模型计算值和实际值的对比Tab.4 Comparison of predicted values of model and actual values

取^x(1)(0)=0，将^x(1)按式 (13) 作累减，检验模型还原值。还原后，模型还原值^x(0)与原始值x(0)的对比如表 5 所列。

表5 模型还原值与原始值的对比Tab.5 Comparison of reduced values of model and original values

故该碟簧刚度的预测模型为

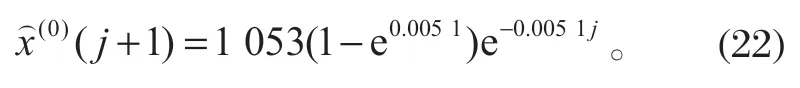
4.2 检验预测模型的精度

根据后验差的检验标准，检验碟簧刚度的预测模型的精度。

已知碟簧刚度的原始数据序列x(0)(j)=(5.400，5.390，5.300，5.280，5.275，5.268)，根据式 (16)，计算碟簧刚度原始数据x(0)(j) 的标准差S1=0.060。

根据模型预测碟簧刚度后，实际值和预测值相减，所得的残差序列q(j)=(0，0.033，0.029，0.022，0.000 3，-0.020)。根据式 (18)，计算残差序列q(j)的标准差S2=0.020 6。C=S2/S1=0.343 ＜ 0.35。

残差q(mean)=0.0211，|q(j) -q(mean)|=(0.021 1，0.011 9，0.007 9，0.000 9，0.020 8，0.018 9)，给定值为 0.674 5S1＝0.040 5，故P=1 ＞ 0.95。

由于C＝0.343 ＜ 0.35，P=1 ＞ 0.95，且相对残差最大为 0.61%。根据表 2 可知，该碟簧刚度的预测模型预测精度较高。因此采用 GM(1,1) 模型对碟形弹簧进行刚度预测，预测效果较好。

5 结语

(1) 可以通过测得闸瓦的最大油压、开闸油压和闸瓦间隙，来求得盘式制动器蝶形弹簧的强度，并进行了有效测量。

(2) 选用灰色理论预测法对碟簧刚度预测进行建模，并以龙东矿副井碟形弹簧为例，采用 GM(1,1) 模型的建模方法，得到了该碟形弹簧刚度的预测模型，并通过后验差检验的方法对预测模型精度进行了检验。检验结果表明，GM(1,1) 模型可靠，预测精度较高。

(3) 通过预测，可以对碟簧刚度的未来发展做出推测，判断碟簧疲劳失效的时间，实现对碟簧刚度的提前预报和控制。