基于GSA-LSSVM的岩石爆破块度预测
王 军,崔志鹏
(江苏南京地质工程勘察院,江苏 南京 210041)
合理的预测岩石的爆破块度分布对于露天矿山的开挖起到了至关重要的作用,并影响后续各项工作的展开。汪学清等[1]构建了神经网络预测模型;周传波[2]研究了基于回归分析理论来预测爆破块度的合理性;潘玉忠等[3]将SVM预测模型引入到爆破块度的预测中;史秀志等[4]验证了LS-SVR预测模型来预测爆破块度的可行性;郑皓文[5]将经过BFO优化后的LSSVM预测模型应用到爆破块度中。
现将GSA-LSSVM预测模型引入到爆破块度的预测当中,利用万有引力搜索算法获得LS-SVM模型中更为合适的关键参数,使得拟合结果更准确。结合已存在的爆破块度统计资料,分别应用三种预测方法对其进行爆破块度的预测。通过对比分析,验证GSA-LSSVM模型的预测效果。
1 GSA-LSSVM算法
1.1 万有引力搜索算法
万有引力搜索算法是由Esmat Rashedi等人提出了一种智能优化算法。该算法通过对物理学中的万有引力这一概念的模拟,得到了一种群体智能优化算法(Gravitational Search Algorithm,GSA)。
万有引力搜索算法的原理:把搜索粒子类比为散落在空间中的若干物体,他们之间的相互作用按照物理学中的万有引力公式来计算。当粒子在运动的过程中,适度值越大惯性质量越大。物体的质量与吸引力成正比,最大质量的物体则吸引着其它物体,不断移动靠近,计算出所需要优化问题的最佳值[6]。
1.2 最小二乘支持向量机
LS-SVM模型的优化评判标准不同于SVM,采取对比目标函数误差的平方项,并将SVM中的不等式约束改为等式约束。相比较SVM,算法在求解过程中,降低了计算难度、加快了求解速度,解决了预测结果的精度因为训练样本数过大受影响的问题[7,8]。
1.3 GSA优化LS-SVM算法参数
LS-SVM模型在本文中的核函数选定为RBF,并经过万有引力搜索优化算法对于模型的正则化参数γ(gam)和内核参数σ(sig2)进行求解,找到参数的最优值。
1.确定算法的迭代次数、粒子一开始所在的位置和所具有的加速度。
2.计算各个粒子的适应值(目标函数误差的平方)。再利用公式(1)更新重力常数:

式中,G0表示在t0时刻G的取值,G0=100;α=20,T为最大迭代次数,T=100。
3.根据公式(2)、(3),并代入适应值,计算出相应粒子的质量大小:
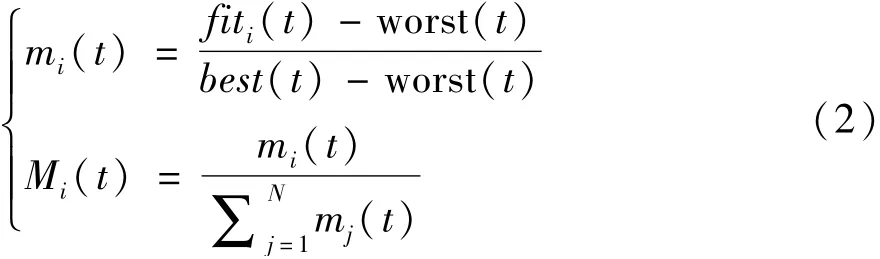
粒子Xi的适应值通过式fiti(t)计算得到。并且在t时刻,粒子Xi的最优解和最差解的计算公式见公式(3):
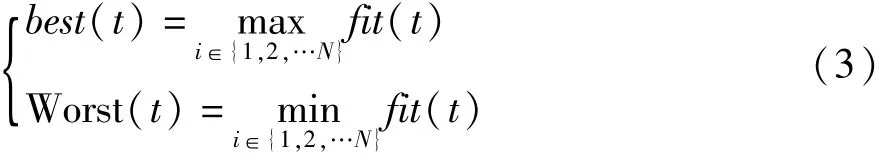
4.按照公式(4)~(8),求解出每个粒子所对应的加速度。
在第k维上,物体j在时刻t时受到物体i的引力大小按公式(4)计算获得:
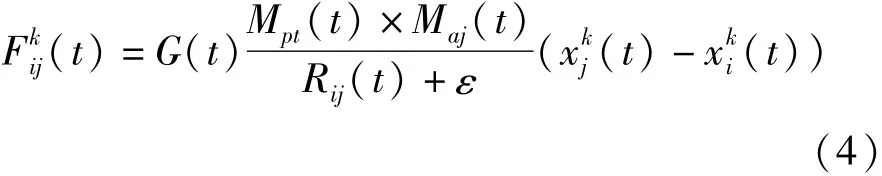
式中,ε为任一小的常量;Maj(t)为物体j受到的惯性质量;G(t)按公式(1)计算得出。
公式(4)中,Rij(t)表示物体Xi与物体Xj的欧氏距离,见公式(5):

在t时刻,第k维Xi所受到的作用力之和,见公式(6):
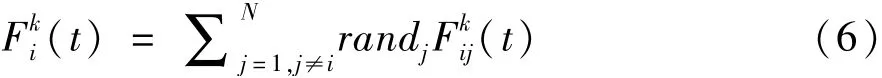
当某一粒子受到其它粒子的作用力时,该粒子就会产生加速度;在第k维上,依据公式(6),物体i受到的加速度具体计算方式如公式(7)所示:

5.不同的粒子的速度计算公式见公式(8),进而更新不同粒子所在的位置。

6.当计算的结果没有达到终止条件时,跳转步骤(2);反之,输出此次算法的最优解。即LS-SVM模型中的参数γ(gam)和σ(sig2)。
1.4 建立GSA-LSSVM模型
在1.3的理论框架下,结合LS-SVM模型,构建出如图1所示的GSA-LSSVM爆破块度预测模型。

图1 GSA-LSSVM预测模型计算流程
1.5 基于GSA-LSSVM模型预测爆破块度
根据文献[9]中已存在的露天矿山爆破块度数据,GSA-LSSVM预测模型进行训练时,只选取块度数据的前33组,后7组数据作为待预测数据;相关数据见表1,各数据参数含义见表2。通过训练前33组数据,得到训练后的模型,用以预测爆破块度大小平均粒径(X50)。通过Matlab软件,编写GSA-LSSVM程序,其中的参数设置:万有引力搜索在寻优过程中的迭代次数设为100,负责搜索最优解的粒子总数设为160。
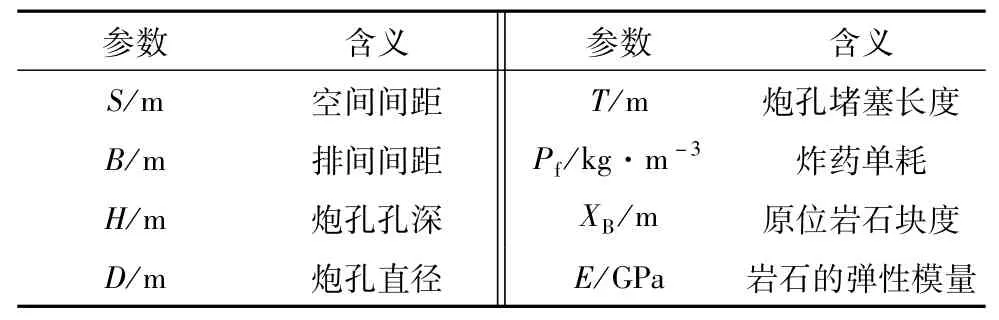
表2 各数据参数含义
经过万有引力搜索算法100次迭代,计算出优化参数γ=68.782、σ=1.563。
2 模型结果对比分析
分别采用GSA-LSSVM、LS-SVM及Kuz-Ram公式,针对爆破块度大小平均粒径这一参数,对表1中后7组的数据进行预测。从预测结果可以看出,GSA-LSSVM的预测结果和实际值非常接近,在三种预测算法中预测精度最高,详细结果见表3。由表3可知,三种不同预测方法相对误差的绝对值平均数分别为:4.57%、12.05%及22.19%;且相较于另外两种预测方法,GSA-LSSVM模型预测的结果拟合度最高。7组预测的数据中,GSA-LSSVM预测模型泛化能力最强,不会出现个别数据预测结果偏离的情况。根据表3中可知:GSA-LSSVM模型对于爆破块度的预测,其预测结果与实际值的相对误差的波动区间为-9.22%~7.73%;LS-SVM模型预测的稳定性不高,存在对个别样本的计算误差值过大的问题;而Kuz-Ram公式的预测效果最差。
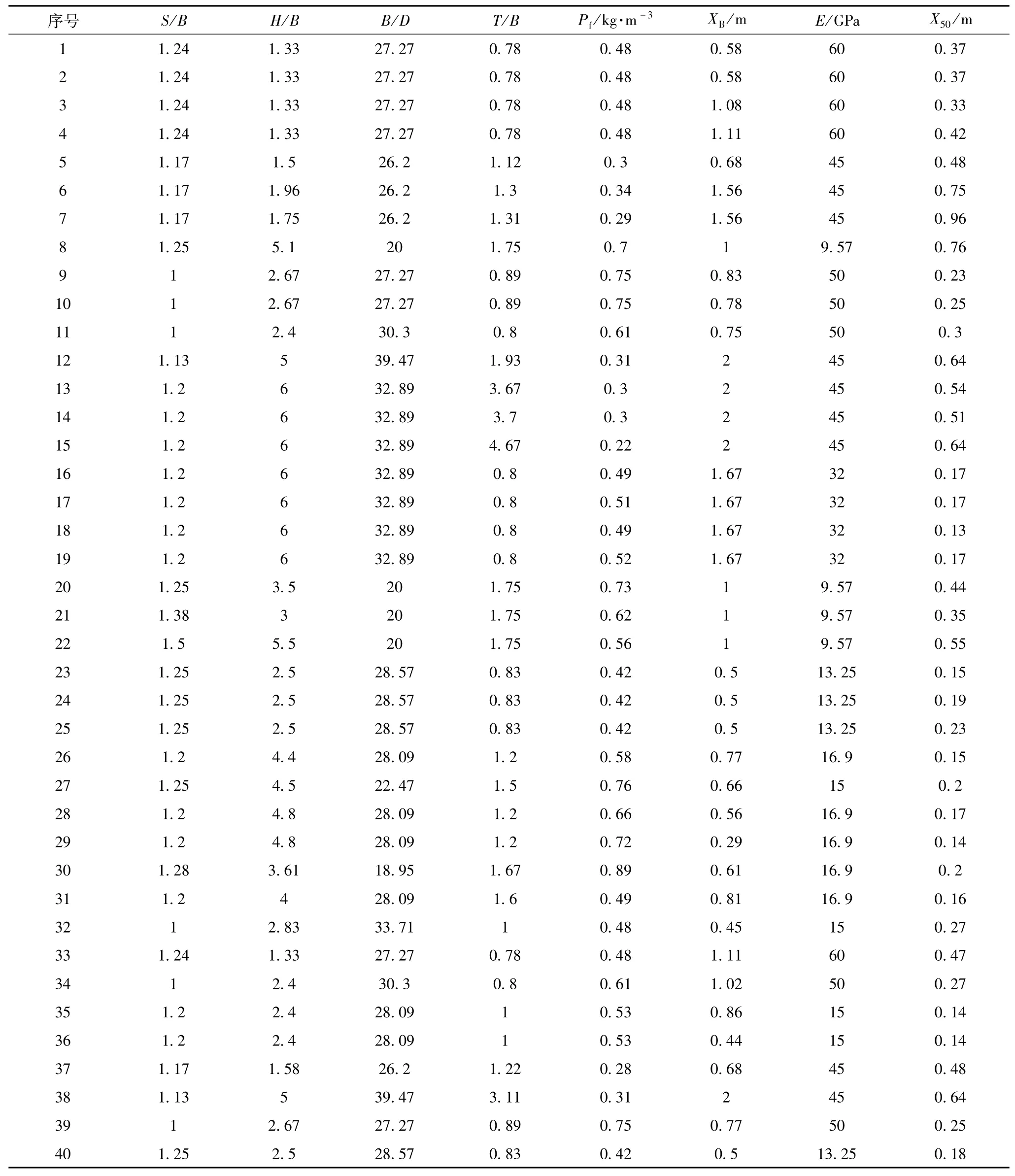
表1 爆破块度统计数据
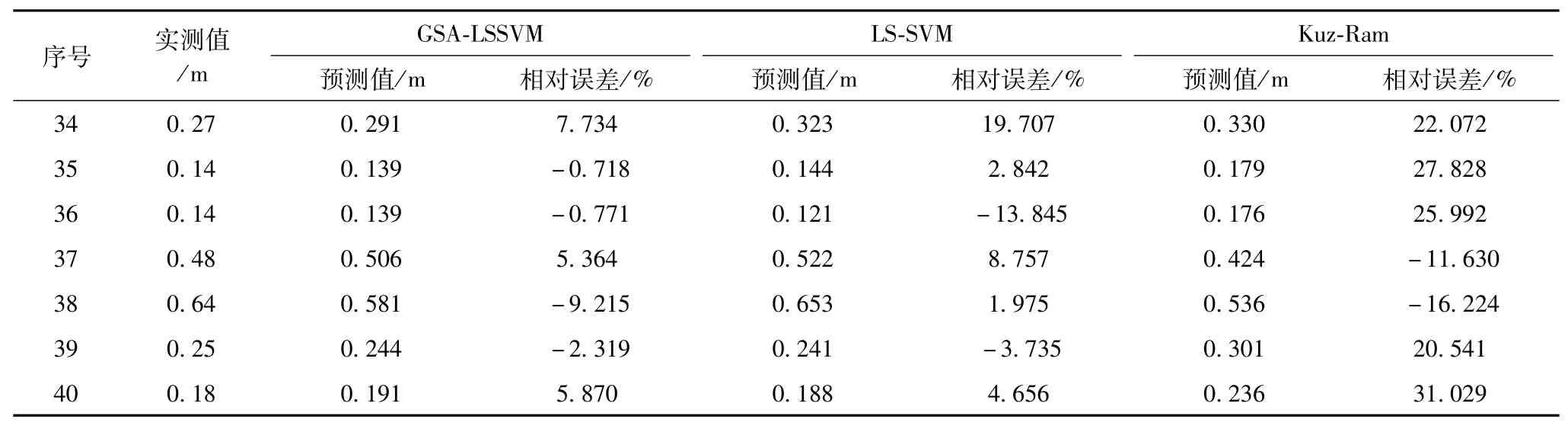
表3 各模型的预测结果对比
因此,将GSA-LSSVM预测模型应用于爆破块度的预测中,其预测精度相较于传统的LS-SVM预测模型和Kuz-Ram公式更高。GSA-LSSVM预测模型计算结果的绝对相对误差值都可以控制在10%以内,符合工程实际应用中对于爆破块度预测精度的要求。
3 结 论
1.运用机器学习的方法对爆破块度进行预测,相比较简单的Kuz-Ram公式,可以尽可能多地把对于爆破有影响的因素考虑进去,结果表示可以得到更好的预测结果。
2.比较GSA-LSSVM和LS-SVM模型对于爆破块度的预测结果,可以得出:通过万有引力搜索优化后的LS-SVM模型,由于其参数γ和σ的数值不再主观地人为选取,模型的泛化能力得到了提高,预测的结果也更加稳定。
3.引入GSA-LSSVM预测模型,经过对现场爆破块度数据的准确预测,佐证了该模型在露天矿山爆破块度的可行性。

