基于颗粒阻尼的U肋加劲板减振降噪初探

孔德睿，张 迅，刘子琦，游颖川，郑宁哲，周靖翔

（西南交通大学 桥梁工程系，成都610031）

钢箱梁因其结构简单、造型美观、环境适应性强等特点，在城市轨道交通、高速铁路的桥梁建设中逐渐得到应用。然而，钢箱梁在受到车辆冲击时产生的噪声具有频谱宽、幅值大、控制难等特点，是当前亟待解决的问题。

现有研究表明，轮轨噪声和桥梁结构噪声是轨道交通噪声的重要来源。目前，轮轨噪声已经得到了较好的控制[1]，但针对桥梁结构噪声的控制研究较少。目前较为成熟的桥梁振动控制方法为设置调谐质量吸振器(Tuned mass damper，TMD)和敷设约束阻尼层(Constrained layer damping，CLD)。但TMD只能针对特定频段减振，CLD存在易老化、适应性差等缺点。为此，本文基于颗粒阻尼(Particle damping，PD)原理，提出一种用于钢箱梁减振降噪的新方法。钢箱梁噪声来源于幅面尺寸较大的板件的局部振动[1-2]。U 肋加劲板是钢箱梁的典型板件，且U 肋具有天然的空腔，这为填充颗粒提供了便利。为此，本文首先对组成钢箱梁的U肋加劲板进行考察。

颗粒阻尼技术的基本原理是将颗粒填充至主体结构空腔内，主体结构振动引起颗粒运动，通过颗粒与颗粒、颗粒与腔壁间的摩擦与碰撞耗散能量[3]。国内外学者陆续提出了颗粒阻尼器的各种简化模型或数值分析方法。Friend和Kinra[4]将颗粒阻尼器简化为一个质量块，采用实测阻尼考虑颗粒运动带来的阻尼效应。胡溧等[5]建立了颗粒阻尼器的粉体力学模型，并研究了颗粒容器参数对减振性能的影响。吴成军等[6]引入气体-颗粒两相流理论，在与有限元法结合后，提出了一种考虑颗粒阻尼的结构振动预估方法。近年来，离散单元法[7](Discrete Element Method，DEM)被广泛应用于研究颗粒运动问题，该方法可以考虑颗粒间及颗粒与容器壁间的相互作用，为多颗粒运动的模拟提供了更准确合理的方法。例如，杨英等[8]基于DEM研究了填充颗粒的尺寸、数量、材料等参数对减振效果的影响。武宏程等[9]基于稳态能量流法和DEM进行了颗粒阻尼器仿真，获得了耗散功率效率、有效动态质量和等效黏性阻尼系数等物理量，并开展了试验验证。

因颗粒阻尼结构简单、作用频谱宽、适应性强等特点，其在机械、航空航天领域得到了广泛应用。例如，Koch 等[10]将颗粒阻尼和蜂窝结构结合后，应用于发动机的减振降噪。王林玉[11]将颗粒阻尼器应用于列车车轮的噪声控制，实测1 600 Hz～5 000 Hz的径向及轴向噪声分别降低了16.28 和14.74 dB(A)。Jie等[12]采用锤击试验验证了颗粒阻尼对钢轨的减振效果，并建立了模拟钢轨与颗粒物非弹性碰撞的解析模型，讨论了激励力、颗粒材质、颗粒质量对减振效果的影响。在土木工程领域，关于颗粒阻尼的相关研究仍处于初步阶段，且主要集中在抗风、抗震等领域。例如，Lu 等[13]对设置颗粒调谐质量阻尼器(Particle Tuned Mass Damper，PTMD)的框架结构在不同地震激励下的振动特性进行了数值模拟和试验研究。结果表明，PTMD 在较宽频带内表现出显著的阻尼效果。Yan 等[14]通过缩尺试验对比研究了地震作用下悬索桥的动力响应。结果表明，添加颗粒阻尼后，结构的位移峰值响应和加速度均方根响应都有较大幅度降低。然而，交通荷载激励下的桥梁振动行为与地震、风等作用时有较大区别。因此，将颗粒阻尼技术应用于钢箱梁车致振动噪声控制的可行性还有待论证。

本文介绍一种基于颗粒阻尼的钢箱梁减振降噪新方法。以钢箱梁U 肋加劲板为研究对象，通过锤击试验和数值仿真手段研究设置颗粒阻尼试件的振动噪声特性，对比分析不同颗粒填充质量、填充位置对减振性能的影响规律。在此基础上，采用数值仿真进行噪声预测。本文的分析方法和研究结论可为今后进一步开展钢箱梁减振降噪优化设计提供参考。

1 试验方案

1.1 试验装置

基于锤击试验原理[15]，本文对填充颗粒阻尼的U肋加劲板缩尺模型进行了振动测试。试验采用力锤(型号：LC1301B)对板件进行激励，用加速度传感器(型号：LC0108T、LC0102T)测量振动响应。为避免边界条件带来的不确定性影响，采用弹性绳将板件悬吊在自行设计的固定支架上，试验装置如图1所示。

图1 试验装置

1.2 缩尺试件

以实际工程中的典型钢箱梁为原型，以1:4为几何缩尺比制作了钢箱梁U肋加劲板模型。模型基板为一1 200 mm×1 000 mm的钢板，通过焊接与U肋进行连接。基板厚度为3 mm，U 肋厚度为2 mm。其他详细尺寸如图2所示。

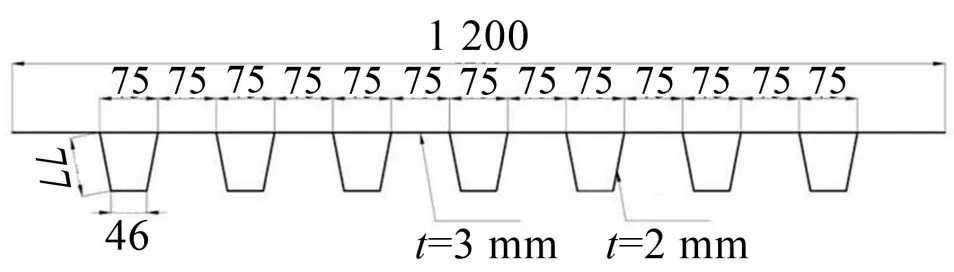
图2 模型尺寸

1.3 测点布置

为测试板件各点的振动响应，在板边缘区域选择3 个激励点，分别位于板件短边的1/4、1/2、3/4 长度处。加速度传感器设置在每个U肋间隔区域的几何中心，即板件长边56.25 mm、225 mm、375 mm、525 mm、675 mm、825 mm、975 mm、1 143.75 mm 位置处。测点位置及编号如图3 所示。图中，三角形表示加速度传感器的位置，箭头表示锤击位置。

图3 频响试验的测点布置

为分析填充颗粒带来的阻尼效应，需要测量板件的平均振动响应。如图4 所示，将板件按照U 肋单元分为15个矩形区域(R1,R2,R3,…,R7及8个U肋间隔区域)，在各区域随机选取3 个位置作为激励点，即在15个区域共设置45个激励点。在图示位置设置加速度传感器，测量每次锤击时的振动响应。根据互易性原理，可求得板件的平均振动响应。

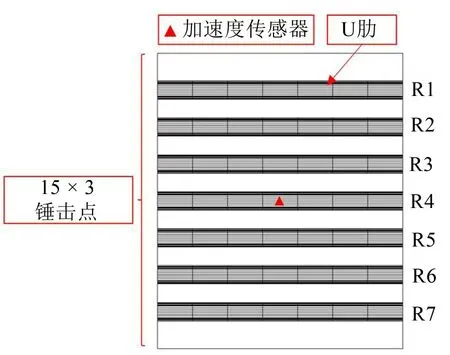
图4 阻尼损耗因子试验的测点布置

1.4 测试工况

为初步探索不同参数下的减振性能，在U 肋中填充不同质量和不同分布位置的颗粒。在实际应用中，颗粒阻尼器作为附属结构，其总质量不宜过大，否则会对桥梁承载能力产生影响。依照经验以加劲板质量的10%为上限，采用直径5 mm 钢珠进行填充，试验照片见图5。填充率最大时，颗粒体积约占U 肋空腔体积的5%，其对U 肋加劲板强度、疲劳等的不利影响基本可忽略。

图5 试验照片

具体工况如表1所示。表中质量填充率为颗粒总重量与原加劲板总重量的比例。所示填充位置Ri(i=1,2,…,7)与图4中标注的U肋编号一致。

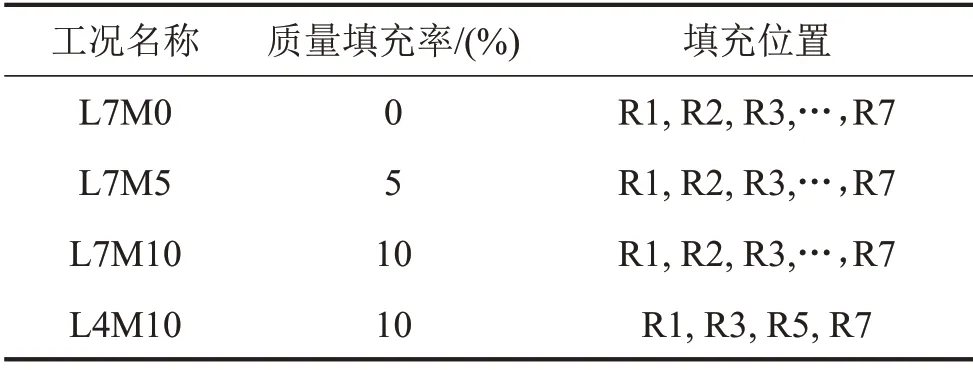
表1 试验工况

2 评价指标

2.1 频响函数

通过力锤对板件进行激励，采集锤击力作为输入信号，同时采集加速度响应作为输出信号。由于每次锤击的激励力不同，为便于对比，采用频响函数描述振动响应的大小。频响函数由输入信号与输出信号的互谱及输入信号的自谱求得[16]，即：

其中：SAF(ω)是输入信号和输出信号的互谱；SFF(ω)是输入信号的自谱；ω表示频率。

2.2 能级差

对于U肋加劲板，在噪声考察频段范围，可将每个测点布置区域（即U 肋间隔区域）视为一个子系统。若其中一个子系统被激励，子系统间的能级差可由下式确定[17]：

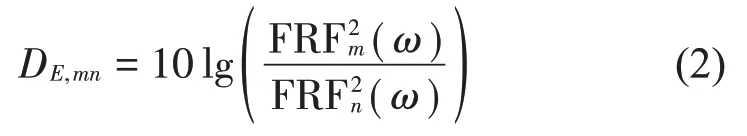
其中：DE,mn表示激励子系统m和响应子系统n之间的能级差；FRFm(ω)为激励子系统m的频响函数，FRFn(ω)表示响应子系统n的频响函数。

2.3 阻尼损耗因子

阻尼损耗因子是描述结构自由振动衰减特性的重要指标。为对比不同颗粒填充情况下结构的振动衰减情况，引入能量法求解阻尼损耗因子[18]，表达式如下：

其中：η为阻尼损耗因子；Yin为驱动点导纳；<|Ytr|2>为空间平均的均方传递导纳；ρ为材料密度；h为板厚；S为板件面积。

3 试验结果分析

3.1 填充质量的影响

保持颗粒填充方式为均匀填充7 条U 肋，分别对质量填充率为0（不填充）、5%、10%（对应表1中的工况L7M0、L7M5、L7M10）的加劲板进行锤击试验，得到试验结果如图6所示。

图6(a)和图6(b)给出了不同填充质量下，#3 和#5 测点的加速度频响函数。对于#3 测点，频响函数峰值在填充颗粒后下降非常明显，其它频率处也有不同程度的下降。对于#5测点，由于到激励位置的距离较远，填充颗粒后振动已经衰减到很小，导致工况L7M5和L7M10的频响函数值差异不大。

图6(c)给出了#1和#7测点的能级差，其中，#1测点处为激励位置。能级差在填充颗粒后显著增大，即振动随距离衰减加快，在125 Hz、315 Hz附近最为明显。填充率为5%～10%时，能级差平均增大约2 dB。

图6(d)对比了阻尼损耗因子的变化。阻尼损耗因子在填充颗粒后变大，说明设置颗粒阻尼有利于振动更快衰减。各频段阻尼损耗因子平均提高至原结构的2倍～2.5倍。其中，在80 Hz以上频段，填充颗粒后的能级差和阻尼因子均显著增大，说明颗粒阻尼具有一定的频变特性，这与其它研究中的结论基本一致。

综合上述对比，与工况L7M5 相比，虽然工况L7M10 的颗粒填充质量增加了一倍，但其减振效果并未得到显著提升（仅略微增加），这可能是由于颗粒在大量填充后发生堆积而未能充分振动引起的。

3.2 填充位置的影响

对于填充位置的对比，保持质量填充率10%不变，分别测试均匀填充7 条U 肋、间隔填充4 条U 肋（对应表1 的工况L7M10、L4M10）下板件的振动响应，测试结果如图7所示。

图7(a)和图7(b)给出了不同填充位置下，#3 和#5测点的加速度频响函数。与原加劲板相比，两种填充方式都能起到显著的减振效果，总体规律与图6(a)和图6(b)相似。

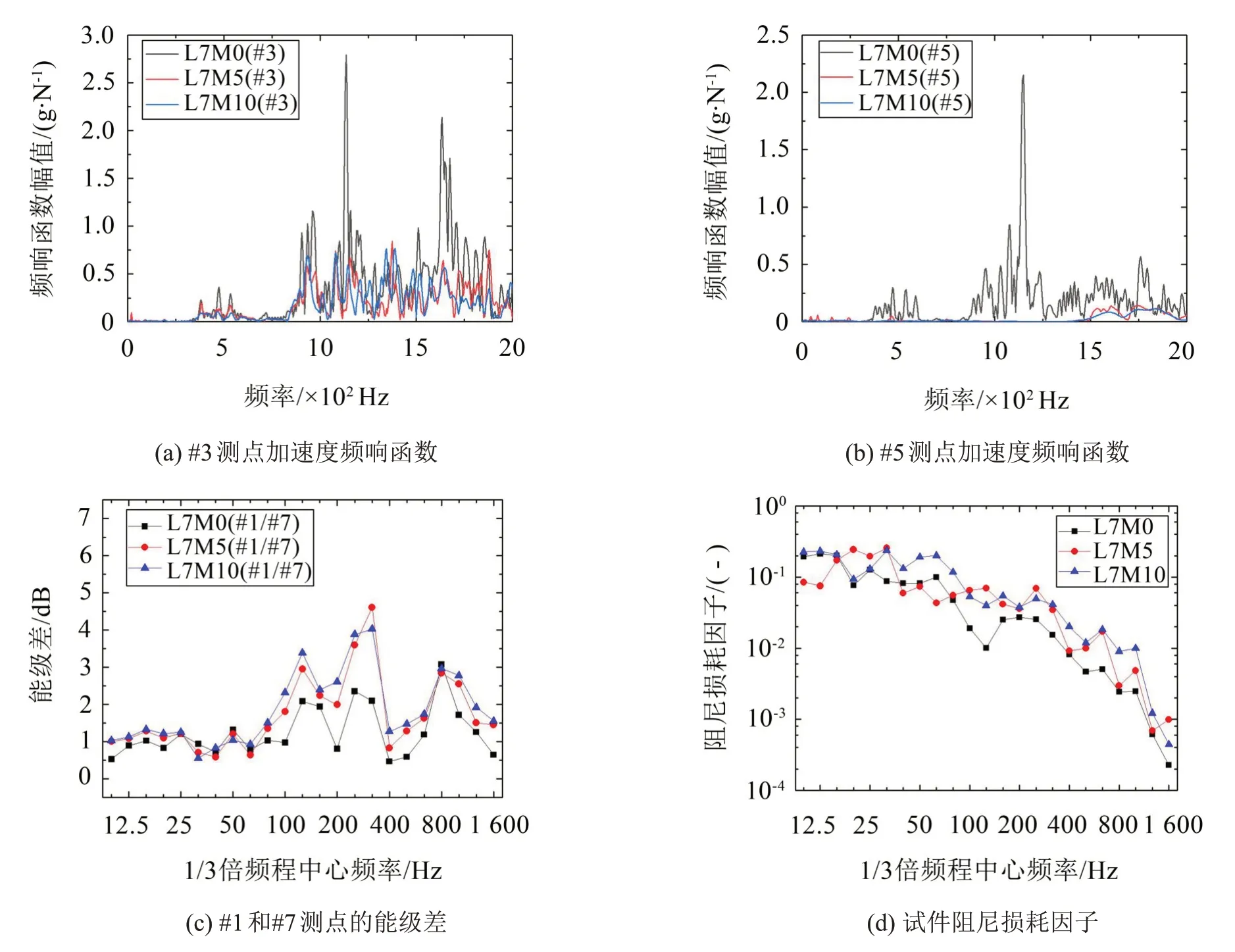
图6 不同填充质量对减振效果的影响

图7(c)给出了#1和#7测点的能级差。填充颗粒后的能级差在80 Hz 以上频段显著增大，在200 Hz处最为明显，增大了约2 dB。在125 Hz和315 Hz等个别频段，均匀填充的减振效果略好于间隔填充。

阻尼损耗因子的测试结果如图7(d)所示。在315 Hz 以上频段时，均匀填充方案的阻尼损耗因子略大于间隔填充方案。

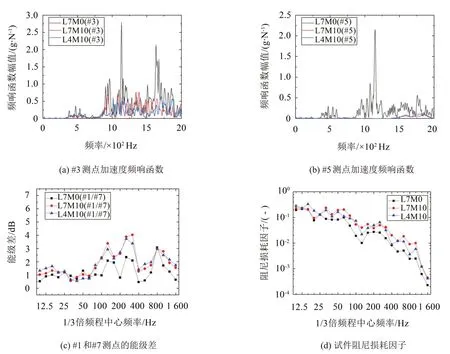
图7 不同填充位置对减振效果的影响

总的来说，两种填充方案均能增大能级差和阻尼损耗因子，但差异并不显著，这可能是由于两种填充方案都以均匀布置为原则，而质量填充率不变。

4 数值仿真分析

4.1 模型验证

本文采用混合有限元-边界元法进行振动噪声预测。首先，在模型试验的基础上，根据实际缩尺模型尺寸，采用ANSYS 软件建立有限元模型。然后，计算其频响函数，将数值计算结果与实测结果对比，验证仿真方法的可靠性。

有限元模型如图8 所示。其中，基板和U 肋均采用Shell181 壳单元模拟，共划分6 885 个节点、7 050个单元。本文将填充颗粒简化为质量块，未考虑颗粒间通过碰撞和摩擦引起的阻尼效应。采用实测阻尼损耗因子对加劲板定义结构阻尼。

图8 有限元模型

仿真与实测结果对比如图9 所示。结果表明，总体上，仿真值与实测值吻合较好，两者的频谱特性一致，验证了有限元分析模拟这一过程的准确性。但是，在个别频率点，实测值与计算值存在一定差异，这可能是由于阻尼损耗因子测量误差、颗粒模拟的简化处理等原因引起的。

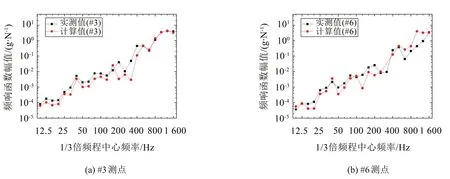
图9 频响函数计算值与实测值对比（工况L7M10）

4.2 噪声预测

基于有限元计算得到的结构振动响应，采用边界元法进行噪声预测。由于实际工程中U肋位于钢箱梁内部，箱体内的噪声难以泄漏出去[19]，因此，计算时仅考虑基板振动所辐射的噪声。将U肋加劲板的边界网格导入LMS Virtual.Lab 软件得到边界元模型，如图10 所示。其中，采用刚性反射面模拟地面声反射效应，提取节点位移作为声学计算的边界条件。

图10 声学边界元模型

图11 给出了4 种工况下的声功率级。由图可知，进行颗粒填充后，板件声功率级总体上在不同频段均表现为下降。其中，630 Hz处最为显著，声功率级降低了约13 dB(A)；在个别频段（如1 250 Hz），板件声功率级轻微增大，这主要是由于填充质量改变了加劲板的振动模态及不同频带的振动能量。

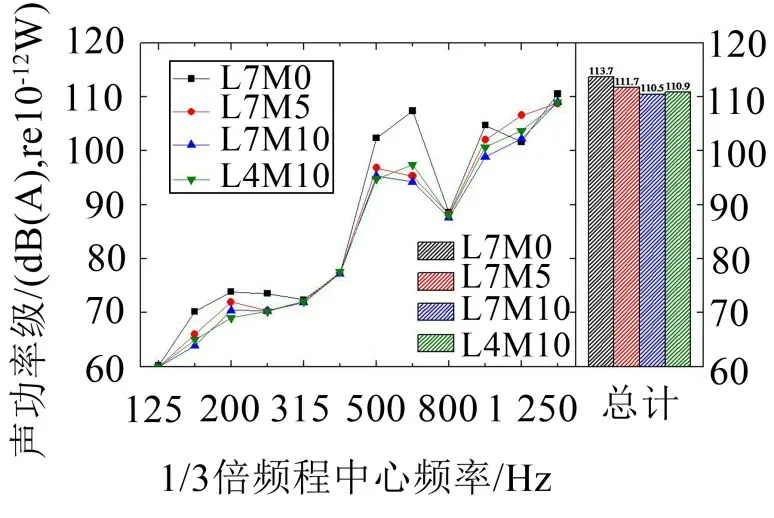
图11 不同测试工况的声功率级对比

质量填充率为5%时，板件各频段的声功率级均显著减小，相比原始加劲板，总声功率级降低了2.0 dB(A)。当质量填充率增至10%时，板件声功率级进一步减小。在均匀填充和间隔填充下，总声功率级分别降低了3.2 dB(A)和2.8 dB(A)。显然，在质量填充率5%的基础上，增加一倍的颗粒填充质量，并不能使降噪效果提升一倍，这与振动试验得到的结论一致。对于不同填充位置，在500 Hz 以上频段，均匀填充的降噪效果略好于间隔填充。

5 结语

（1）对于U肋加劲板结构，颗粒阻尼可以起到显著的减振降噪效果，且作用频带较宽，具有工程应用前景。均匀填充10%质量时，各频段阻尼损耗因子平均提高至原结构的2 倍～2.5 倍，总声功率级降低了3.2 dB(A)。

（2）增加颗粒质量对减振效果有积极影响，本研究中10%填充质量的能级差和阻尼损耗因子略大于5%填充质量，但并未显著增加。

（3）保持填充质量不变时，均匀填充和间隔填充两种方案的减振效果未见明显差异，但均匀填充方案在500 Hz以上频段的降噪效果略好。

（4）颗粒阻尼的减振降噪效果具有一定的频率相关性，但对减振和降噪的有效频率并不一致。其成因有待进一步研究，这一现象同时也为颗粒阻尼的优化设计提供了思路。

本文针对钢箱梁典型板件——U肋加劲板的颗粒阻尼减振降噪效果进行了初步探讨，验证了该措施的有效性。但是，当前所开展的测试工况较少，填充质量和填充位置的工况较为有限。今后，还需对颗粒材质、颗粒尺寸、颗粒分布、颗粒用量、颗粒容器设计等作进一步讨论。此外，声振分析中颗粒阻尼的精确模拟方法还有待深入研究。