古筝声音品质主观评价指标的CRNN量化方法

付 鹏，邓小伟，周 力，余征跃

（1.上海交通大学 船舶海洋与建筑工程学院，上海200240；2.上海民族乐器一厂，上海201101）

中国传统民族乐器是中国文化的瑰宝，而古筝作为其中最具有代表性的乐器之一，其普及率在我国所有民族乐器中位居前列，对弘扬中国民族文化有着极为重要的意义。

截止目前，业界暂未建立完整的古筝声音品质评价体系，主要依靠专家的主观评价来确定古筝音质的好坏，无法满足生产和流通的需求。音质的主观评价是指，一组被测人听同一段声音后，将内心对音质的主观感受予以语言或文字表达。主观评价主要通过实验方法获得，具体包括排序法、评分法、成对比较法、语义细分法等[1]。但由于每位专家的经历和体验存在差异，他们使用的主观评价指标不尽相同。即使对同一指标，各位专家的理解也不一样。这导致主观评价的随意性和偶然性较大[2]。

为了解决主观评价的这些缺点，国内外学者将问题分解为构建适当的特征、规定合理的声学特征与主观指标之间的关系两部分，提出了一些将声音品质与声学特征量化分析的方法。这些方法包括通过频谱质心来描述人对音色的感知和声音信号之间关联[3]，以及通过合成音乐的方式，定量地修改声音信号，更系统地将声学特征与音色感知相关联[4-6]。还有用来提取声音信号中多维描述符的工具箱被设计出来，为了方便在大型声音数据库中寻找音色与多维声学特征的关系[7]。

这些方法的特征基于手工设计（Hand-crafted）。但要通过手工设计来构建出针对目标任务辨别度大、相关性高、鲁棒性强的特征难度较大[8]。而深度神经网络因为其具有自动提取局部特征的能力，可以将构造特征和构建特征与声音品质关系这两个问题进行联合优化。所以近年来，在处理音频信号相关问题时，利用各类频谱图作为输入的深度学习方法已经得到了广泛的应用[9-11]。又由于音频数据的特殊性，其本身就可视为一种时间序列，故有多人尝试卷积循环神经网络（Convolution Recurrent Neural Network，CRNN）在处理音频数据中的可行性[12-13]。这是一种将深度学习中的卷积神经网络（Convolutional Neural Network，CNN）和循环神经网络（Recurrent Neural Network，RNN）融合使用的神经网络。

本文将在此基础上，利用深度学习设计一种可以对古筝音质进行量化评价的方法。首先，通过实验构建古筝音质评价的数据集，确定由5 个主观评价指标构成的古筝总体评价体系，并将这五个指标作为量化的对象。然后，使用CNN中的深度残差网络（Residual Network，ResNet）和RNN中的长短时记忆网络（Long short-term memory，LSTM）联合构成的CRNN 网络模型，将预处理后的古筝音频信息作为输入，综合多位专家对各指标的评价结果作为模型监督，训练CRNN模型。最后，检验模型在乐器声音品质量化中的效果。

1 相关研究方法

1.1 深度残差网络

深度残差网络（ResNet）的设计，是为了解决深度学习模型中的层数堆叠到一定数量之后，单纯层数的增加有时不仅难以提升模型效果，还会导致预测能力大幅降低的问题[14]。

其主要思想是在网络中增加了如图1所示的直连结构，使后层网络可以直接得到前层网络的输入。图中，X为上层输入，F(X)为将输入X经两层卷积层变换后的输出。该结构使得模型在多层网络下依旧能保证信息的完整性，并且整个网络只需要学习输入和输出之间的残差，简化了每层的学习目标和难度。最终该结构使得模型可以通过大幅增加深度获得与之对应增长的预测性能。并且即使在相同深度下，使用深度残差网络的模型性能也比普通的深度学习模型有着很大的提升。

图1 深度残差网络的直连结构

1.2 长短时记忆网络

普通的神经网络只能单独地处理每个输入，前后输入之间是完全无关的。但是，在本文的音质评价任务中，音频数据在时间维度上的前后逻辑是个重要的信息，而RNN能够更好地处理这类任务。

长短时记忆网络是RNN 中的一种。其基础子结构如图2所示。图中，Xt为输入，ht为输出。普通RNN能够处理一定的短序列问题，但由于没有记忆功能，只是简单输入的堆叠，较早的信息很难被传递到当前序列中。所以，普通RNN难以处理长序列任务。而LSTM 采用图2 所示的结构，使用输入门、遗忘门、输出门3种门来保持和控制信息，以便更好地处理长短期序列[15]。

图2 LSTM基础结构

2 量化方法

古筝声音品质主观指标的量化方法流程如图3所示。声音信号输入后，可以获得一个代表音质好坏的向量，以此作为古筝声学品质各指标的量化结果。

图3 量化方法流程框图

2.1 音频数据集的构建

由于古筝音质评价任务的特殊性，现公开范围内暂无相关成熟的数据集。所以，本文首先要对所需数据集进行构建。数据集的构建包括两个部分，一部分是对古筝音频数据进行采集，另一部分是对音频数据的声音品质进行标定。

（1）音频数据的采集

随机挑选符合出厂要求的22把古筝后，进行随机编号。邀请专业古筝演奏者分别使用每一把古筝按照标准化的内容进行弹奏，并且尽量保证弹琴力度和节奏的统一性。弹奏音频全程使用SONY PCM-D50录音棒进行录制，采样标准为16位脉冲编码调制（Pulse Code Modulation，PCM）音频格式，采样频率为44.1 kHz。录制地点为厂商的专用录音室。

（2）声音品质的标定

为了最大程度地减少主观评价的随意性和偶然性，我们邀请了6 位古筝专家对每把古筝弹奏的音质进行综合评价。首先对专家们的评价进行整理，包括整合相同含义、不同表达的术语，舍弃一些极少使用且意义不明的指标。然后结合查找到的文献资料和国家标准[16-17]，确定了古筝的总体评价由“纯净度，圆润度，明亮度，平衡度，柔和度”5个主观评价指标构成。

最后，综合整理6 位专家在这5 个指标上的评价，对每把古筝进行标定。具体方法为，忽略在某个指标上没有评价的专家后，分别计算每个指标上专家认为好或者坏的个数，数量多的作为这个指标的标定结果。

2.2 语谱图的提取

在音频领域中，CNN 输入一般是二维的频谱图，可以对局部特征进行提取，学习局部特征的关联性。

语谱图是频谱图中的一种，通过对音频数据做短时傅里叶变换（Short-Time Fourier Transform，STFT）得到，计算前需要确定STFT 的几个必要参数：

nfft：对时域数据x(n)做傅立叶变换(Fourier Transform，FFT)时，一帧所包含的采样点个数，一般应取2 的幂次。音乐相关的音频数据在做FFT 时，帧长最好在20 ms～93 ms 之间，由于录音时的采样频率sr 为44.1 kHz，为了满足上述帧长条件，选择nfft等于4 096。

hop_length：定义每两帧之间的滑移值，一般取FFT分辨率的1/4，也就是1 024。

其算法流程如图4所示，通过对声音信号分帧，加窗做FFT，最后堆叠而成。

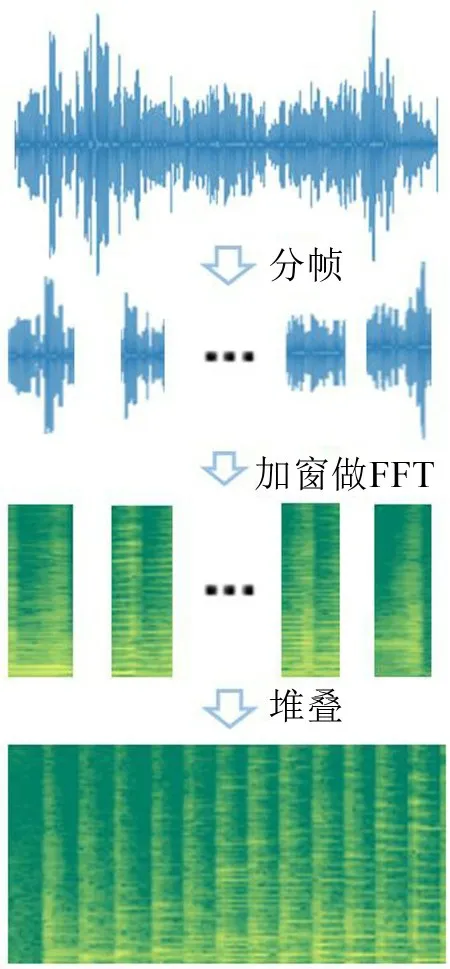
图4 短时傅里叶变换算法流程

图像是语谱图的一种可视化表达，其实际是一个以横轴为时间、纵轴为频率的二维数据，对应二维点的值代表幅值。语谱图同时包含了声音的时域、频域信息，保留了声音信号的绝大多数特征，所以本文中选择其作为CNN的输入。

2.3 预处理

为了将数据输入到神经网络中，需要将原始音频信号通过短时傅里叶变换得到的语谱图分割为长宽分别为h和w的片段。根据公式（1）和公式（2），语谱图所能表达的最大时间和最高频率与语谱图大小的转换关系，可以知道每个语谱图片段均可表达时间维度[ 0,tmax]和频率维度的信息。对于当前的音频数据，在时间维度，每个片段分割为3秒恰好涵盖了每个单音从起始到衰减的整个过程。在频率维度，对于音域范围为73 Hz到1 174 Hz的古筝来说，2 400 Hz 可以覆盖到绝大部分的基频和倍频能量。所以将语谱图分割为长宽均为224的片段。求得tmax=3s,fmax=2 400 Hz，可以满足上面的要求。

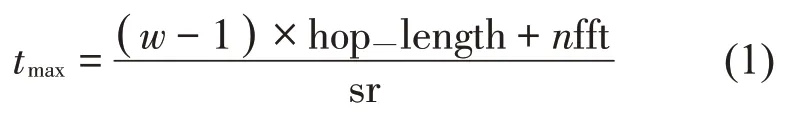
为了检测神经网络学习的效果，还需将数据分为训练集、验证集、测试集3个部分。其中训练集用于训练模型，验证集用于模型训练时判断模型是否收敛，测试集用来测试模型优劣。本文采取的方法是，将每把琴的语谱图随机分为连续的，长度比为7:2:1的片段。将第一份归入训练集，第二份归入验证集，第三份归入测试集。

2.4 数据增强

由于缺少相关公开数据集，数据集只能自己采集，这就不可避免地导致数据集在种类和数量上都少于成熟的数据集。为了丰富数据，增强神经网络模型的性能，防止神经网络模型过拟合，本文对原始数据集进行数据增强。

具体来说，本文采用在训练和预测时随机分割的方法来替代事先由人工将音频分割成224×224的片段。根据每把古筝原始音频数据的长度，平均每把琴的音频数据可以被分为3 000份～4 000份。

对于分割后的数据，为了增加模型对一些部分频率信息丢失和含噪声的声音片段的鲁棒性，本文参考由Google提出的音频数据增强方法[18]：

(1)应用频率屏蔽，对每个输入片段屏蔽连续f个频率维度[f0,f0+f]，屏蔽即对其置0。其中f从[ 0,20 ]中随机选择，f0从[ 0,fmax-f]中随机选择。

(2)应用时间屏蔽，对每个输入片段屏蔽连续t个时间维度[t0,t0+t]，其中t从[ 0,20 ]中随机选择，t0从[ 0,tmax-t]中随机选择。

2.5 CRNN构建和指标量化

CRNN 模型结构包含CNN 和RNN，其中CNN选择ResNet，RNN 使用LSTM。搭建好的CRNN 模型结构为先通过ResNet对语谱图提取出局部特征，之后将其继续输入给LSTM提取时序特征。

当前任务需要在主观评价的5个维度上同时做出判断。所以，本文选择使用多任务联合学习的方式，将每个主观评价指标作为子任务进行并行学习。

具体的实现方法是，在CRNN结构设计完成后，将其提取到的特征输入给全连接层共同预测出5维向量x，之后分别经由公式（3）计算得出每个主观评价指标较好的概率。

将作为最后各项指标的量化结果。

本文CRNN 模型的损失函数以交叉熵（Cross entropy）函数为基础，设计构建针对5维指标的损失函数：

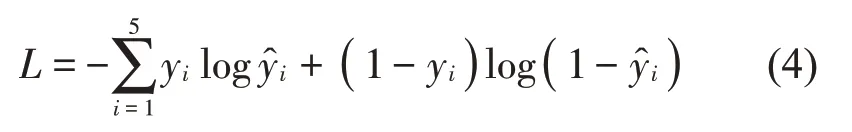
其中：yi代表每个指标综合专家意见的标定结果，其取值0为该指标较差，1为该指标较好。

该损失函数在指标较好，即yi等于1时，为关于的单调递减函数。在yi等于0时，为关于单调递增函数。即无论实际指标为何种结果，预测该指标与实际结果相同的概率越大，损失越小。所以，模型的目的从抽象的评价指标的判断转为具体的对损失函数L的最小值最优化问题。

2.6 CRNN模型训练

模型训练时，根据2.4 提到的数据增强方法，先由网络自己随机选择语谱图分割位置，并将连续的5张大小均为224×224 的语谱图在通道上堆叠形成224×224×5 的特征图作为模型的输入。训练过程中，神经网络通过计算损失函数L的梯度，对其中的参数进行更新，实现寻找L的最小值的目的。为了使模型得到更快更好的训练效果，采用ADAMS 优化器对模型进行优化，并设置初始学习率为3×10-4。

3 结果分析

3.1 CRNN模型与专家评价结果对比

在音频收集时我们得到了6位专家对每把古筝的评价结果，但由于部分专家对古筝音质评价的态度较为严谨，不轻易评价古筝声音在这5 个指标中的好坏。所以，最终选择了给予有效评价最多的4位专家，计算各位专家评价与古筝各项指标标定结果相比的准确率，如表1所示。

将测试集中数据输入给构建的CRNN模型进行计算后，得到模型输出的向量x。根据公式（3）可以分别得到五个指标好坏的概率。设置阈值为0.5，当待预测指标的概率值>05时，判断其为好，反之为坏。计算模型在各项指标上预测结果与古筝各项指标标定结果相比的准确率，如表2所示。

表2 每位专家评价在各项指标上的准确率/(%)

表2 CRNN模型评价的准确率/(%)

由表1和表2对比可以看出，每位专家在各项指标的准确率在70%和80%之间，而根据CRNN模型得到的准确率均大于85%。CRNN模型预测各项指标的准确率均优于由单一专家主观评价的准确率，达到多位专家主观评价的综合效果。

3.2 CRNN模型实际应用效果

CRNN模型最后得出的结果实际为每个指标好坏的概率，因此我们可以将作为得分对每个指标做进一步量化。

另外挑选高低两种档次的古筝分别录制其音频样本，通过本文CRNN 量化方法分别得到两把琴5个评价指标的得分，如表3所示。

表3 不同档次古筝的量化得分

将得分画成雷达图如图5 所示，可以直观地区分出两者的差异。高档琴的各项指标得分都较高且分值均匀，而低档琴虽有个别指标得分较高，但其他指标表现较差。由此可以直观清晰地看出两把琴的优劣，达到主观评价的效果。

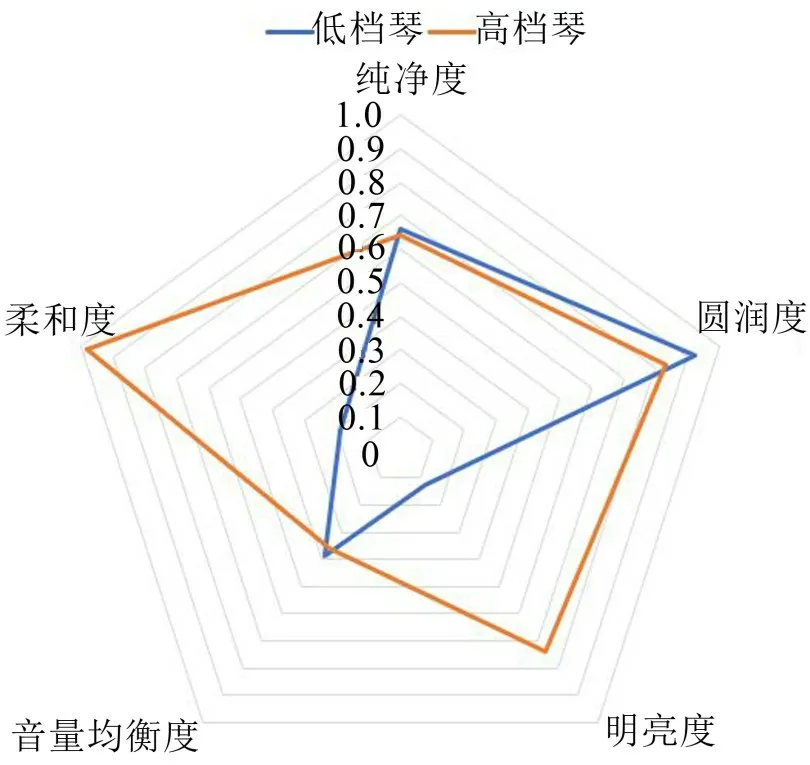
图5 不同档次古筝的评价图

4 结语

本文通过设计实验收集古筝音频数据和专家们对其声音品质的判断，提出了一种基于CRNN 模型的声音品质主观评价量化方法。通过对比分析和实际应用发现，该方法可以较为准确地对古筝的声音品质作出量化，并且由于使用了数据增强的手段，所以同时具有较好的噪声鲁棒性。相比于多位专家主观评价的传统方法，本文提出的方法有着方便快捷，成本更低的优点。

深度学习方法对数据集质量和数量的要求较高，目前这方面的公开数据集仍较为稀缺。本文以古筝为对象已经验证了该量化方法的可行性，但由于数据采集的单一性，其泛化能力可能不足。未来针对这些问题，会进一步收集更多样化的数据加入。优化出更为准确且泛化性更高的模型，提高量化准确度。该方法除可应用于古筝等民族乐器主观评价外，也可以对西洋乐器声音品质的主观评价量化有借鉴作用。