几何非线性效应对受迫振动索理论解的影响评估

梁浩博，刘小会，2，杨曙光，闵光云，伍 川

（1.重庆交通大学 土木工程学院，重庆400074；2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆400074；3.国网河南省电力公司 电力科学研究院，郑州450052)

基于经济发展的需求，国内外很多工程领域都广泛使用大跨度的索结构，例如桥梁工程领域的斜拉桥和悬索桥、电气工程领域的高压输电线路等。然而索结构因其自身重量轻、柔度大以及低阻尼的特点，很容易在外力荷载作用下出现大幅度的振动，呈现出非常明显的非线性现象。索的这种大幅振动极易导致整个工程结构出现损坏。因此，关于索结构的非线性动力学研究是个很重要的课题。

关于索的非线性动力学研究早在18 世纪就开展了。随后，Routh[1]推导出悬索的运动方程并得到悬索固有频率。Irvine 等[2]在1974年推导出水平索固有振动方程式，并对拉索的模态、频率等参数进行系统的分析研究。文献[3]基于哈密顿变分原理并采用Galerkin 离散法推导出单档覆冰悬索运动方程。文献[4]引入无量纲参数推导出受温度变化影响的悬索面内非线性偏微分方程，利用Galerkin 法得到离散后的微分方程。文献[5]同样采用Galerkin法，建立一个两自由度悬索离散模型，对悬索的1:2内共振进行了研究。文献[6]采用Galerkin方法得到悬索的时滞微分方程，以对其主共振进行分析。

由于大跨度输电线路实质上也属于索结构，因此关于输电线路的学术研究同样可以为拉索研究带来指导性意见。Rega等[7]引入无量纲参数并基于哈密顿变分原理推导出输电线面内非线性偏微分方程，接着应用Galerkin 法和多尺度法求解该方程。汪峰等[8]基于Galerkin 模态截断法和多尺度法推导出斜拉索面内振动方程并得到幅频响应方程，分析了梯度温度场等因素对振动的影响。文献[9]基于悬链法和热应力理论推导出考虑温度效应的覆冰导线偏微分方程，接着采用Galerkin 法和多尺度法将其离散和求解。受限于非线性理论的发展，上述众多学者关于理论方程的求解都是基于模态叠加法对系统进行了线性化处理，最终得到结构的近似分析解。该处理方法虽然在一定程度上简化了计算，但对于这些具有几何非线性的结构是否可以直接使用，会不会对结果造成误差等等，这些问题仍有待商榷。

国内学者赵跃宇等[10]以悬索为例，并引入新的无量纲参数得到无量纲悬索面内运动方程，对结构非线性动力学中常用的Galerkin法和直接法进行了对比，发现离散法并不适用于所有结构非线性动力学的求解。文献[11]中，作者采用小参数法得到久期项导致的悬索振动形态，并与Galerkin 离散法得到的相应振动形态进行对比，最终验证了小参数法的可行性。然而上述文章均是以两种算法的对比为主要目的，针对Galerkin 离散法本身的适用性并未作出详细区分。

另外，Rega 等[7]和赵跃宇等[10]分别引入了不同的无量纲参数将运动方程无量纲化，但却并未有学者对这两种无量纲参数对系统非线性的影响以及两种无量纲方法是否适用于所有结构非线性系统做详细的研究。

因此，本文基于简单的单跨拉索力学模型以及振动理论，针对Galerkin 离散法和两种无量纲方法的适用性进行详细讨论。

1 基于Galerkin方法的水平拉索受迫振动数值解

1.1 力学模型及两种无量纲方法

设单跨拉索两端处于同一水平高度，在自重作用下位于如图1所示的XOY平面内，X轴沿拉索弦向方向，Y轴沿拉索竖向垂度方向。拉索跨径为l，其变形可以分为两部分：

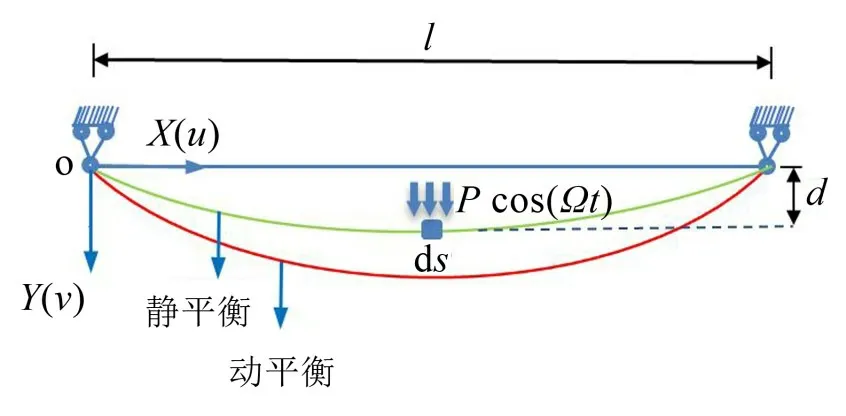
图1 单跨水平拉索力学模型

(1) 拉索在自重作用下处于静平衡状态，垂度为d；

(2)拉索在面内外部荷载作用下产生处于XOY平面内的位移。

考虑到拉索在受到几何非线性和三向耦合时所引发的动力学问题很复杂，本文将模型简化，做出如下假定：

(2)本构关系符合胡克定律；

(3) 不考虑弯曲、扭转以及剪切，忽略其轴向运动；

(4)不考虑张力沿拉索轴向的变化。

图1所示理论模型中，考虑沿拉索Y向施加均布简谐激励荷载Pcos(Ωt)，P为激励幅值，Ω为简谐激励的频率。取图1中拉索处于静平衡状态下的微段ds进行研究，可以得到单跨拉索的面内运动方程：

式中：H为拉索在自重作用下达到静平衡状态时的水平张力，v为沿拉索面内Y向的位移，E为拉索弹性模量，A为拉索横截面积，m为拉索单位长度质量，μ为黏性阻尼系数。

引入无量纲参数：

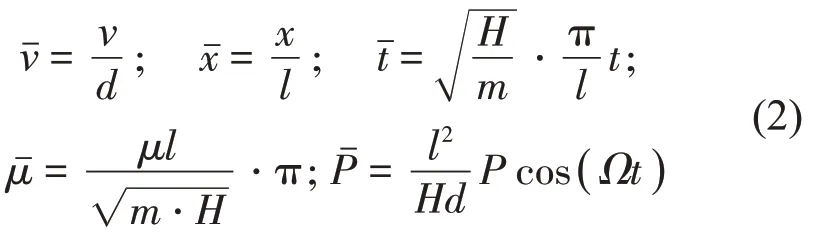
将上述参数代入式(1)，得到拉索面内无量纲运动方程：

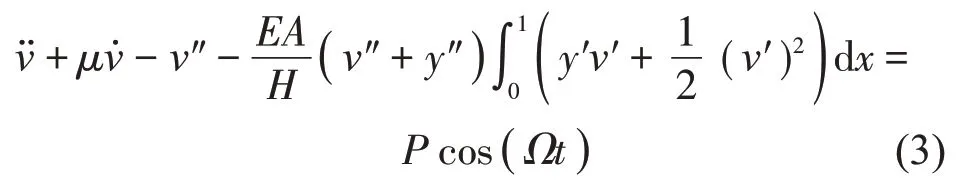
为了方便后文书写，式(3)中各无量纲参数的上划线“-”均已省略（后文同）。式(3)中“v′”表示对无量纲时间t求1 阶导，“v″”表示对无量纲位移x求2阶导。

由于v是关于时间t和位移x的参数，根据Galerkin理论，可将其分离变量为：

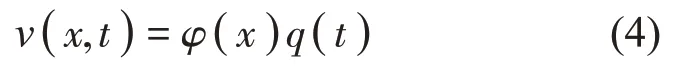
其中：φ(x)为模态函数，q(t)为时间函数。

将式(4)代入式(3)中，并在方程两端乘以模态函数φ(x)，接着在x∈[0，1]内进行积分，可得到：

式中：

其中：λ2为Irvine 参数，见式(7)。该参数可以反映拉索的垂度效应。λ的值越大，拉索的垂度越大。ωn即为无量纲化后的频率，ω表示面内自振等效圆频率，f为拉索自振频率。式(5)中q上方的点“˙”和“˙˙”，分别表示对无量纲时间t求1阶导和2阶导。

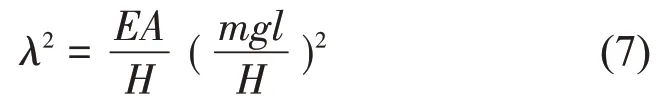
g是重力加速度。

引入另一种无量纲参数：

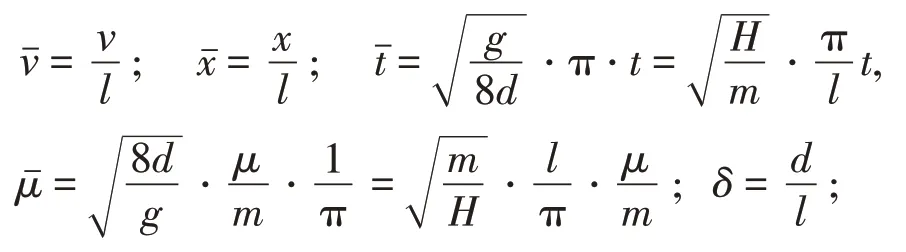
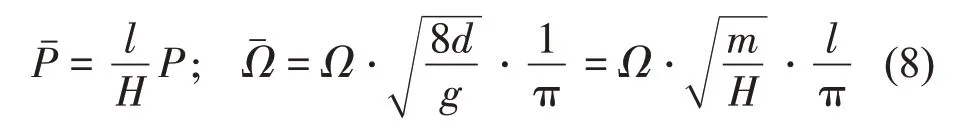
式中：δ为垂跨比，张力H可表示为：

取其无量纲静态垂度曲线为：

将上述无量纲参数代入式(1)，可得拉索面内无量纲运动方程：

式中：

同样，该式通过模态叠加法可得到：

式中：

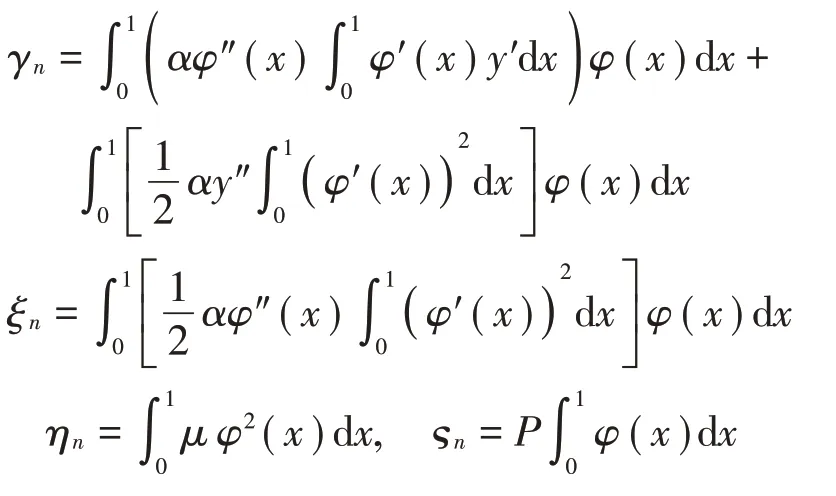
由于两种无量纲方法主要区别在于竖向位移v所除是d还是l，故下文均以无量纲d″和无量纲l″来分别表示两种不同的无量纲方法。

1.2 单跨水平拉索面内频率及模态

研究拉索在外激励作用下产生受迫振动的现象，首先要研究其频率和对应模态。其中模态分为两种形式，对称模态与反对称模态。本文主要研究对称模态。

取方程(3)的线性部分（忽略阻尼项）及边界条件：

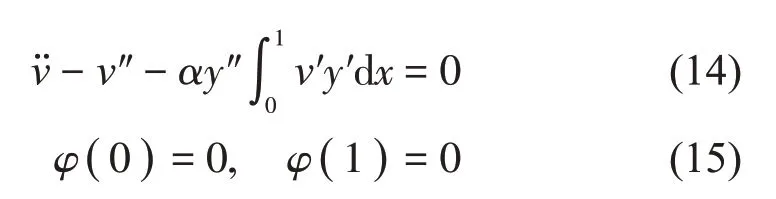
令v=φ(x)eiωt并将其代入式(15)中，结合边界条件可得拉索面内模态函数：

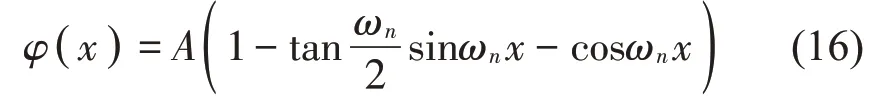
取正交模态：

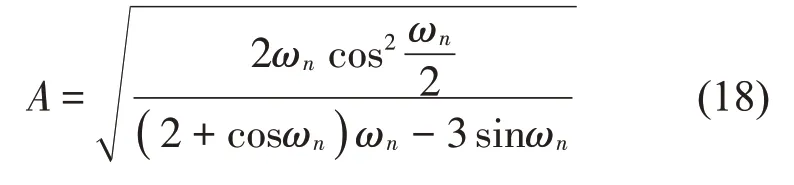
ωn可由超越方程式(19)求得：

1.3 两种无量纲方法的数值解对比

观察式(1)的拉索面内运动方程发现，方程的形式较为复杂，且变量较多，不利于进行数值求解。而引入无量纲参数就可以减少变量数目，便于后续求解。同时，由于对参数进行了无量纲化，更方便做不同工况下的参数对比。

但是可以注意到两种方法关于面内竖向位移v的处理方法是不同的，这是否会导致两种方法所得结果出现一定的差异，本文考虑将这两种方法做对比（拉索物理参数均取自文献[12]，详见表1）。

表1 拉索物理参数

文中系统的黏性阻尼系数μ均采用瑞利阻尼，具体计算方法如下：

取α为0.02，β为0，将其代入公式中，即可得到阻尼比ξ。而阻尼μ则可由公式μ=2ξωm得到。

由式(7)可知：受到张力和垂度的影响，不同参数对应的拉索非线性强度各不相同，故本文选取λ为等于1π、3π、7π、9π等4种工况进行研究。4种工况下的具体参数见表2。

表2 不同Irvine参数对应的物理参数

将表1 和表2 具体参数导入MATLAB 程序中，即可运行得到系统时间历程曲线，如图2所示。

2018年1—8月，全国国有及国有控股企业（本月报所称全国国有及国有控股企业，包括中央管理企业、中央部门和单位所属企业以及36个省、自治区、直辖市、计划单列市的地方国有及国有控股企业，不含国有金融类企业。以下简称国有企业）经济运行态势良好。偿债能力和盈利能力比上年同期均有所提升，利润增幅高于收入10.4个百分点，钢铁等行业利润增幅较高。

通过观察图2可知：无量纲d方法相较于无量纲l方法所得幅值略大，尤其在λ=1π 时，差距较为明显，但随着λ值的增大，这种差距逐渐缩小，直至忽略不计；同时由表3可知：两种无量纲方法均会使系统非线性系数增大，尤其以无量纲l方法增加最大。

图2 两种无量纲方法时间历程曲线

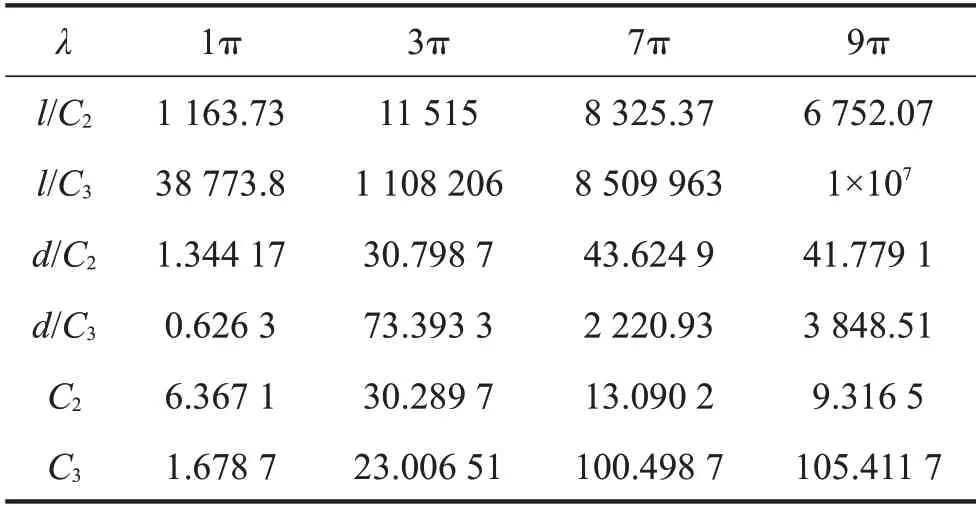
表3 不同Irvine参数对应的非线性项

2 基于多尺度法的受迫振动理论解

由于拉索运动方程比较复杂，一般难以求得其精确解，且拉索振动属于弱非线性问题，因此可采取近似的解析方法求解。传统的解析方法主要包括：渐进法、多尺度法、平均法等，而多尺度法是其中应用得最广泛的方法。本文亦采用多尺度法来分析系统响应。

为了满足多尺度法的求解条件，首先对式(1)直接采用模态叠加法进行离散。接着，为了使非线性项，外部激励和阻尼出现在同阶中，引入无量纲小量ε，经过化简后，式(1)即可转化为：

式中：

上式(21)中的等效圆频率、平方和立方非线性项系数以及外激励中所包含的I的取值可表示为：

为了方便书写，后文已将式(20)和式(21)中的“*”忽略。

引入以下参数：

其中：σ为调谐参数。

将式(23)代入式(20)中，并比较ε同次幂项的系数，可得：

式(24)的解可用指数形式表示为：

此时，A可写成极坐标形式：

式中：a表示振幅，β表示相位。

将其代入式(25)中，即可得到：

消除式(28)中的久期项，可得：

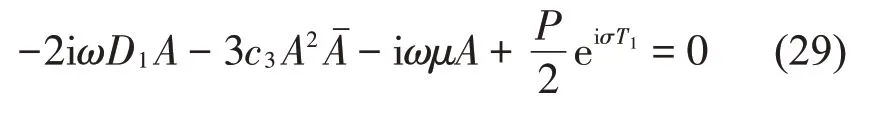
将上式进行化简可得：

并将A代入式(30)可得到：

分离实部和虚部可得：

引入：

方程即可转化为：

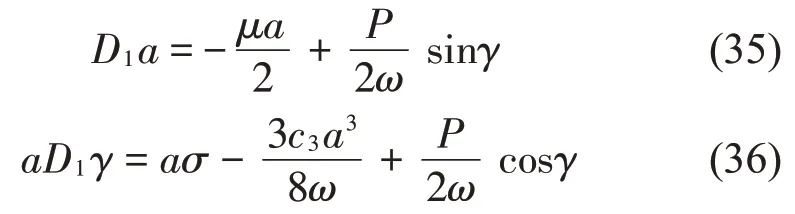
令D1a=0，D1γ=0可得出以下方程：

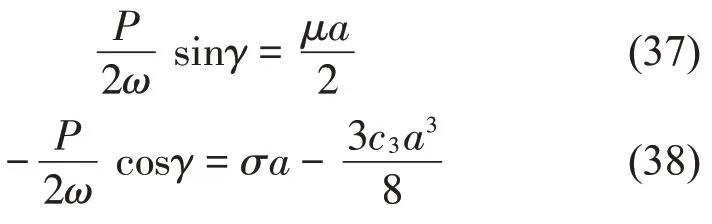
上述方程两端各自平方并相加即可得幅频响应方程：

由式(39)并结合表1中的拉索物理参数，即可得出拉索的幅频响应曲线，见图3。

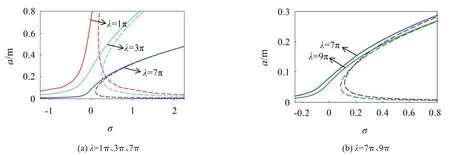
图3 幅频响应曲线

如图3 所示：横坐标σ表示调谐参数（无量纲），纵坐标a表示幅值（单位为m）。实线表示稳定值，虚线表示不稳定值。

结合曲线和式(23)所引入的小量可知：当调谐参数σ=0时，外激励频率与系统固有圆频率相等，此时拉索产生主共振。同时，随着λ增大，系统非线性不断增强，曲线出现跳跃现象，幅值也出现明显的衰减。

当σ=0时，将参数代入式(39)中可得到系统稳定后的理论幅值为：(1π)0.589 27 m；(3π)0.210 062 m；(7π)0.062 395 m；(9π)0.051 052 m。

将该理论幅值与1.3 节中两种无量纲方法稳定后的幅值对比后发现：无量纲d方法与理论解的误差依次为：22 %(1π)，3.797 %(3π)、2.124 %(7π)、0.878%(9π)；无量纲l方法与理论解的误差依次为:4.323 %(1π)、3.688 %(3π)、2.624 %(7π)、3.005 %(9π)，总体来看无量纲l方法所得结果更接近理论解。

3 不同方法结果的对比

3.1 单跨水平拉索有限元模型

由于拉索在受到覆冰、外部激励等因素的影响时，易产生较大的振动幅度。因此不易通过实验来获取数据，以验证理论，而这时采用有限元方法数值模拟拉索的振动便成为了研究拉索受迫振动的重要手段[13-14]。

然而在实际工程中，拉索振动时具有明显的几何非线性效应，通过有限元模拟所得的结果是否会考虑到这种非线性效应的影响?是否会产生误差?因此，本文通过建立有限元模型，来模拟拉索的受迫振动，并将结果与数值解作对比。

采用杆单元模拟单跨拉索，网格数量为100。由于本文仅讨论研究拉索在垂直方向上的运动，故在拉索两端施加边界条件，将其完全固定。

采用参数化建模后，第一步：在拉索上施加重力荷载，以对其进行非线性静力变形分析。第二步：频率分析，提取拉索的前30 阶固有频率及模态，并与基于理论所得的固有频率作对比,见表4。第三步，沿拉索竖向施加均匀外力激励，以使其产生面内的竖向振动，力的大小设置为0.7 N(相当于施加大小为5.6 m/s风速的风荷载)。阻尼项选取瑞利阻尼。

表4 不同垂度下拉索第一阶面内对称模态自振频率对比

3.2 共振时的数值解与理论解对比

重点考虑最危险的情形，即拉索产生主共振。将表1和表2的拉索物理参数分别输入ABAQUS软件和MATLAB程序中，即可运行得到系统时间历程曲线。由第2节在本文方法基础上分别使用两种无量纲参数所得数值解与理论解相比的误差可知：无量纲l方法所得结果与理论解吻合良好。限于篇幅，本文仅给出使用无量纲l方法时本文方法所得数值解与有限元解的对比结果，如图4至图7所示。

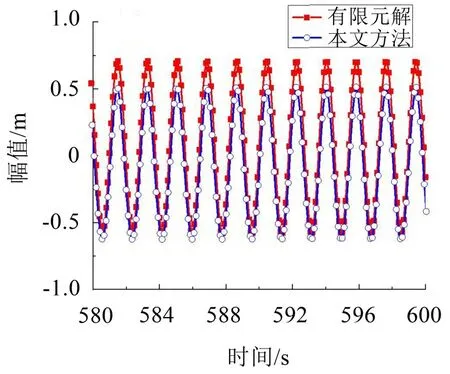
图4 (λ=1π)拉索面内对称模态共振时间历程曲线

图5 (λ=3π)拉索面内对称模态共振时间历程曲线

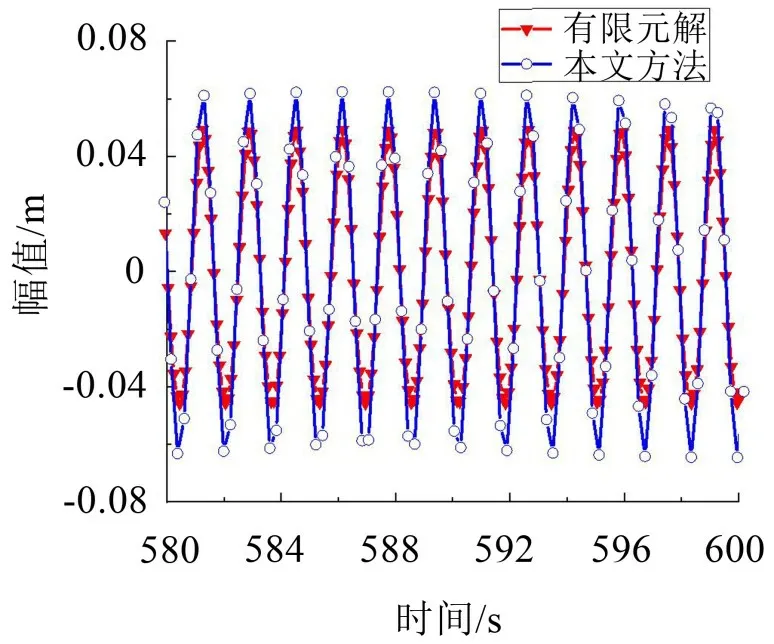
图6 (λ=7π)拉索面内对称模态共振时间历程曲线

图7 (λ=9π)拉索面内对称模态共振时间历程曲线

如图4、图5所示：当λ取1π、3π时，有限元解出现往幅值为0的水平线上方偏移的现象，而本文方法的计算结果则出现向下偏离的现象（偏移量见表5）。造成该现象的主要原因是由于系统中平方非线性项的存在，如：式(5)中的c2、式(13)中的γn以及式(20)中的εc2项，具体数值见表3；该项越大，偏上或偏下的程度也就越大。同时，由于λ取1π、3π 时系统的振动幅值较大，其偏移也就相对更加明显。当λ=7π和9π时，由于本身幅值很小，加之平方非线性项在7π 和9π 时逐步减小，故其偏移程度也相对很小。

表5 共振时拉索的时间历程曲线偏移量

如图4至图7所示并结合表6、表7可以发现：本文方法所得数值解与上节幅频响应函数计算得出的理论解吻合良好，而有限元解与本文方法所得数值解相比则出现了不同程度的幅值差距。这种差距呈现出随着λ增大而增大的趋势。

表6 无量纲l方法所得数值解与理论解对比

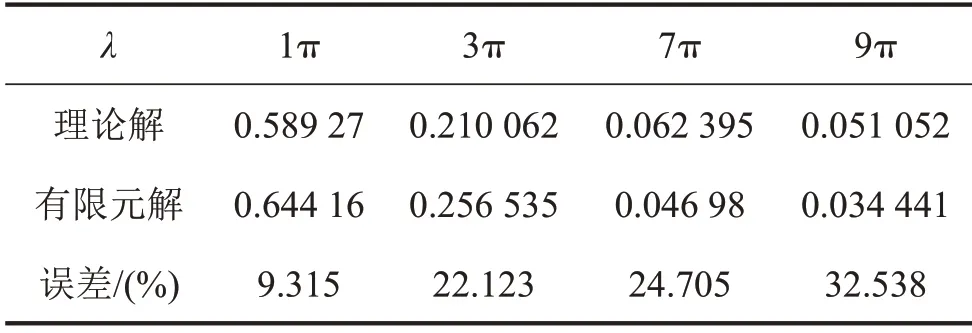
表7 有限元解与理论解对比

如图6、图7 所示：本文方法所得数值解较之有限元解更大，其原因在于当使用有限元软件进行模拟时，能够真实的体现非线性动力响应，而本文方法得到的数值解是采用了Galerkin离散法近似化的运动方程，这种近似化的方法弱化了非线性。综合上述系统非线性越强，幅值就越小的结论，最终出现了图6、图7所示结果。

3.3 非共振时的幅值比较

就实际情况而言，拉索因发生共振而造成破坏的情况极少，大多是在覆冰和风载两种主要影响因素下所造成的非共振区的大幅度振动。因此本节通过将施加在拉索上的外激励频率（ω=4 rad/s）偏离其固有圆频率并采取与上一节相同的模式来进行对比。其中，λ=1π、3π、7π、9π 时频率偏离大小分别为：0.501 9 rad/s、-0.591 6 rad/s、0.137 7 rad/s、0.433 0 rad/s（外激励频率减去固有圆频率）。

如图9 至图12 所示：其部分现象与共振区现象一致。而图9所示结果出现了有限元解与本文方法所得数值解差距较大的现象。初步结合表2 判断，造成该现象的原因是所施加的外荷载激励频率小于λ=3π时的固有圆频率（ω=4.59 rad/s）。为验证该判断，本文取ω=4.8 rad/s 时，采用无量纲l方法进行再次对比，结果如图12所示，表明判断正确。

图8 (λ=1π)拉索面内对称模态非共振时间历程曲线

图9 (λ=3π)拉索面内对称模态非共振时间历程曲线

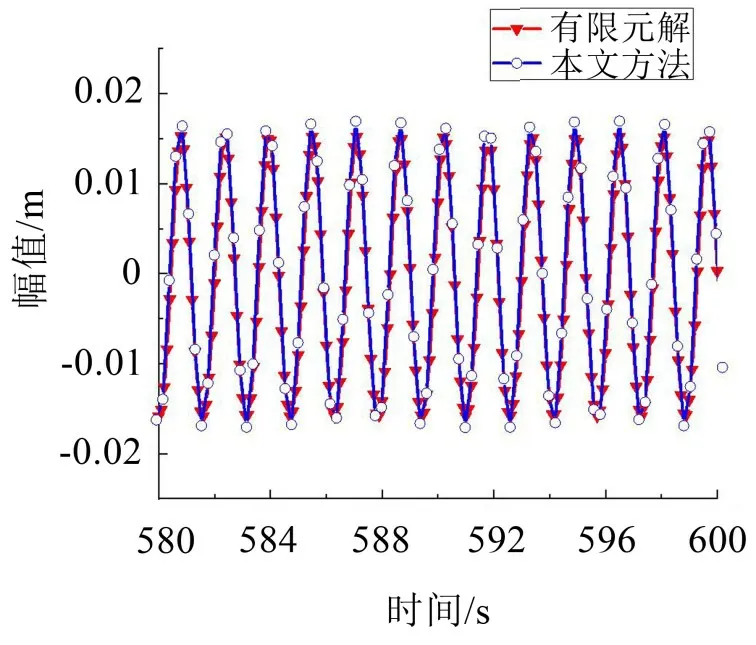
图10 (λ=7π)拉索面内对称模态非共振时间历程曲线

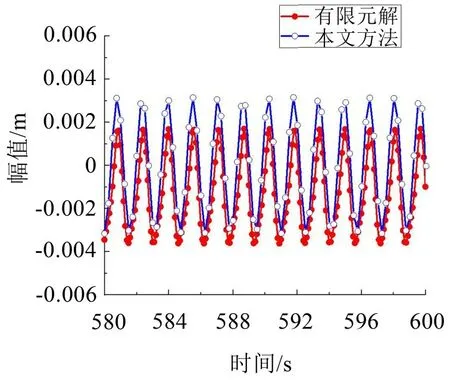
图11 (λ=9π)拉索面内对称模态非共振时间历程曲线

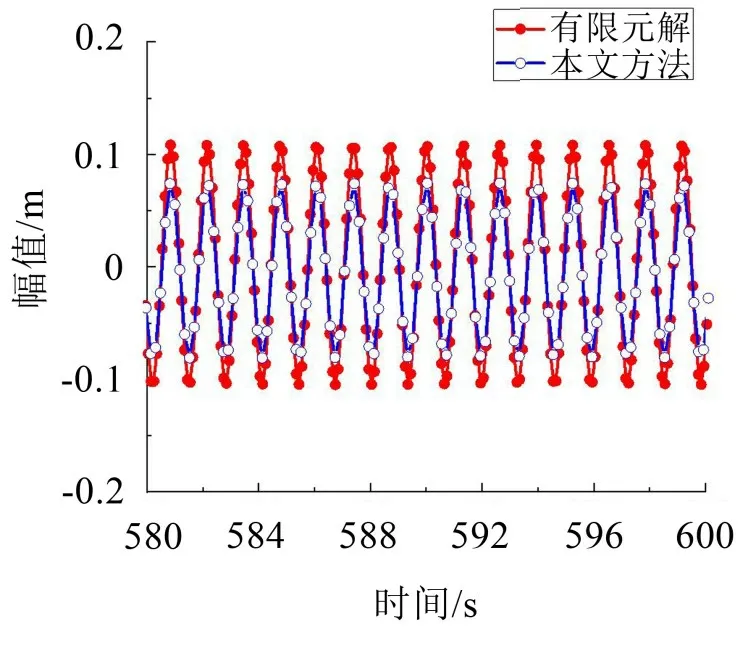
图12 (λ=3π)拉索面内对称模态非共振(ω=4.8 rad/s)时间历程曲线

由图（12）可以发现：当所施加外部激励频率为4 rad/s 时，图中所呈现出的现象并无明显规律。分析可知：在非共振区，本文方法所得数值解与有限元解的差距，主要取决于外激励频率的大小与其圆频率的差距。外激励频率与圆频率的差距越大，本文方法所得数值解与有限元解的差距也就越大。同时，随着λ值的变大，其时间历程曲线就相对不规则，甚至出现相位差，如图11所示。

4 结语

本文通过应用Galerkin离散法得出拉索无量纲面内振动方程，并运用多尺度法得到系统的幅频响应曲线，最后分别通过ABAQUS 和MATLAB 进行了4 种工况的数值模拟和有限元分析对比，主要得出以下结论：

（1）随着系统非线性的增强，幅值逐渐减小，而有限元解与理论解的差距则逐渐增大，说明Galerkin离散法对于弱非线性系统适用性更高，系统非线性越强，误差就越大。

（2）系统的平方非线性项会造成有限元解和本文方法所得结果分别产生向上和向下的偏移。

（3）随着λ值的增大，两种无量纲方法差距微小，总体而言经过无量纲l方法得到的运动方程所得的系统时间历程曲线更接近理论解；为了使结果更精确，当系统非线性强时可采用无量纲d方法，系统非线性弱时则采用无量纲l方法较好。