基于正态云期望和方差距离的语言型多属性决策方法研究
龚艳冰,徐绪堪,刘高峰
(河海大学a.商学院;b.统计与数据科学研究所;c.常州市工业大数据挖掘与知识管理重点实验室,江苏 常州 213022)
一、引 言
自然语言是人类思维的基本工具,语言值是自然语言中的基本单元,是人类思维的基本细胞。在决策的过程中,由于客观事物的复杂性、人类思维的模糊性和决策环境的不确定性等因素影响,使得决策者往往用语言变量来表示判断信息。比如,决策者在考虑供应商的选择、企业技术协同创新能力以及人才的选拔等问题时,往往不容易给出确切的定量评价信息,决策者在对某一对象的性能进行评价时,常常采用“很好”“好”“一般”“差”和“很差”等语言变量表达决策信息,这也符合人们的思维习惯[1]。因此,语言变量已经成为一种更加直观、方便的表示不确定信息的方法,如何科学地表达和处理不确定语言变量,充分挖掘语言决策信息中的不确定关联信息,如何构建科学合理的多属性决策方法实现不确定信息的有效输出,在不确定语言型多属性决策领域具有重要的意义。目前,已有一些处理不确定语言变量的理论和方法,例如采用模糊语言术语集、区间语言术语集、二元语义法等,但是这些方法在处理不确定语言变量时均存在一些不足,如不能够同时处理语言变量中的模糊和随机不确定性等[2-7]。李德毅和杜鹢在概率论和模糊数学的基础上提出了云模型理论,通过期望、熵和超熵三个数字特征构造二阶的正态分布实现了定性概念与定量表示之间的双向认知转换[8]。近年来,云模型已经开始广泛应用于不确定语言型多属性决策问题中,与其他方法相比,云模型不仅能够有效刻画语言变量的模糊性和随机关联性,而且能够更好地克服定性与定量转换过程中的信息损失问题[9-16]。
在基于云模型的语言型多属性决策过程中,需要对正态云表示的决策方案进行量化比较或排序,这就涉及到不同云模型之间的距离测度。云模型距离度量在语言型多属性决策中扮演着很重要的角色,好的距离度量方法可以很大程度上提高其决策的科学性和合理性。目前,学者们对正态云的距离度量方法已经开展了一系列研究,例如,王坚强等提出正态云的Hamming距离来定义不同正态云之间的相对距离,Hamming距离是将正态云的熵和超熵看成期望的权重系数,容易削弱熵和超熵的作用,其计算得到的距离整体偏小,需要在特定的条件下使用[10]。王新生等提出正态云的Euclidean距离来定义不同正态云之间的相对距离,Euclidean距离将期望、熵和超熵同等对待,又过于强调超熵的作用,当三个数字特征相差较大时,其计算得到的距离整体又偏大[17]。
本文从云模型的几何特征出发,充分考虑正态云的形状和位置,以正态云期望曲线和含熵期望曲线的期望和方差距离为切入点,给出一种正态云期望和方差的Manhattan距离。在此基础上,采用云模型将决策者对备选方案的语言评价值进行云量化;采用正态云不确定度最小化思想确定属性权重,并利用CWAA算子合成得到方案综合云;利用基于云Manhattan距离的TOPSIS方法从正态云距离度量的角度考查候选方案与正负理想方案之间的相似程度,提出基于正态云期望和方差距离的语言型多属性决策方法。
二、云模型概念及性质
定义1[8]:设C(Ex,En,He)是定量论域U上的定性概念,且x(x∈U)是定性概念C的一次随机实现,服从高斯分布x~N(Ex,En′2);其中En′又是服从以En为期望,He2为方差的高斯分布En′~N(En,He2)的一次随机实现,且x对定性概念C的确定度满足
(1)
则称上述x在论域U上的分布为正态云(高斯云)。显然,正态云可以用期望Ex、熵En和超熵He三个数字特征来表征一个概念,其中期望Ex表示云滴在论域空间分布中的数学期望,熵En表示定性概念的不确定性度量,由概念的随机性和模糊性共同决定,超熵He表示熵的熵,是熵的不确定性度量。
定义2[8]:若正态云模型C(Ex,En,He)的云滴x满足x~N(Ex,Hn′2)且En′~N(En,He2),则称
(2)
为云模型C(Ex,En,He)的期望曲线。期望曲线是云滴集合的骨架,所有的云滴都在期望曲线附近随机波动,因此期望曲线是研究正态云几何特征的重要方法,但是,期望曲线忽视了正态云超熵He的作用,具有一定的缺陷,刘常昱等证明了由正态云发生器算法生成的正态云模型(1)产生的云滴分布是一个服从期望为Ex,方差为En2+He2的随机变量[18],为此龚艳冰等定义了如下正态云含熵期望曲线。
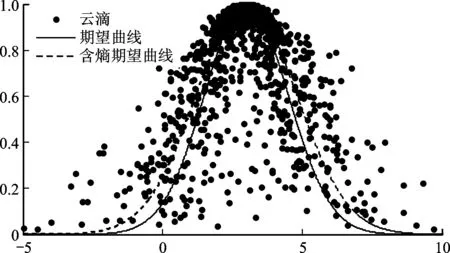
图1 正态云期望曲线和含熵期望曲线
定义3[19]:若随机变量x满足:x~N(Ex,En′2),其中En′~N(En,He2)且En≠0,则称
(3)
为正态云的含熵期望曲线。当超熵He=0,含熵期望曲线就退化为期望曲线(如图1所示),含熵期望曲线包含正态云的三个数字特征,因而能够更好地反映正态云的几何特征。


(4)
依据上述正态云分布的概率密度函数,可证明正态云模型具有下列统计性质[8]:
(1)正态云分布的数学期望E(X)=Ex
(3)正态云分布的方差D(X)=En2+He2
从正态云分布的统计性质(1)~(3)可知,正态云的期望曲线和含熵期望曲线的数学期望(Ex)和方差(En2、En2+He2)分别对应三个数字特征,因此,为了有效度量两朵正态云之间的距离关系,可以通过建立关于正态云期望和方差的距离测度来衡量。
三、正态云不确定度和期望方差距离
正态云模型的三个数字特征中熵En和超熵He是描述概念的不确定性度量,其中超熵是熵的不确定性度量,也可以称为二阶熵。对于一个常识性概念,被普遍接受的程度越高,则超熵越小;反之,对于难以形成共识的概念,则超熵较大。超熵的引入为常识知识的表示和度量提供了帮助[8]。如果超熵He=0,数据样本对概念的确定度是确定的,正态云分布就退化为正态分布,因此,为了反映正态云的二阶不确定性,可以利用正态云的期望曲线和含熵期望曲线的方差(En2、En2+He2)之比定义一个新概念——正态云不确定度。
定义4:正态云模型C(Ex,En,He)的不确定度定义为
(5)
则正态云的不确定度ρ具有如下性质:
(2)当超熵He=0时,ρ=0;
(3)如果两朵正态云C1和C2相同,则有ρ(C1)=ρ(C2)。
证明:性质(2)和(3)显然成立。
对于性质(1),显然有0≦ρ≦1,


定义5[10]:设两朵正态云C1(Ex1,En1,He1)和C2(Ex2,En2,He2),则C1和C2之间的Hamming距离为
(6)
定义6[17]:设两朵正态云C1(Ex1,En1,He1)和C2(Ex2,En2,He2),则C1和C2之间的Euclidean距离为
(7)
一个合理的正态云距离要能很好地反映两朵正态云之间的位置和形状,不仅需要充分利用正态云的三个数字特征,而且需要考虑三个数字特征不同程度的影响,本文从云模型的几何特征出发,利用三个数字特征期望、方差和不确定度方差(二阶方差)给出下列基于期望方差的Manhattan距离:
(8)
其中,ρ1和ρ2为正态云的不确定度,反映的是期望曲线与含熵期望曲线的不确定程度,当超熵越大,正态云期望曲线和含熵期望曲线的差距越大,样本对概念的不确定度越高。将不确定度式(5)代入距离式(8)可得基于期望方差的Manhattan距离简化为:
(9)
特别地,若两朵正态云C1(Ex,En,He1)和C2(Ex,En,He2)的期望Ex和熵En相同,则C1和C2之间的Hamming距离、Euclidean距离和Manhattan距离分别为
dE(C1,C2)=|He2-He1|;

为了更好地说明本文提出的云模型距离度量方法有效,下面利用现有文献中的示例数据进行仿真实验,并且与现有方法进行比较。

图2 三朵正态云模型及含熵期望曲线
实例:文献[13]给出3朵正态云模型N1=(3,3.123,2.05),N2=(2,3,1),N3=(1.585,3.556,1.358),这3朵正态云模型具有熵和超熵较大的特征(如图2),也即模糊性和随机性都较大,因此,在计算它们的距离时,不但要考虑熵的因素也必须要考虑超熵的作用。

表1 三种正态云距离度量方法比较
按照Manhattan距离式(9)可得三朵正态云的相对距离,其中N1和N3的距离最大(1.523 5),N1和N2的距离次之(1.103 6),N2和N3的距离最小(0.699 4),这个结果与图2的直观印象一致。由表1容易发现,三朵正态云的Manhattan距离和Euclidean距离的结果一致,但是Manhattan距离方法效果更好,Euclidean距离放大了超熵的作用,导致距离偏大;而Hamming距离得到N1和N2的距离最小(0.087 2),这个结果与图2的直观印象是矛盾的,这是由于Hamming距离弱化了熵和超熵的作用,易使结果不准确。
四、基于云距离的语言型多属性决策应用
(一)决策流程
不确定语言型多属性决策问题一般可以描述为给定一组可行的备选方案A={A1,A2,…,An}和相应的属性集U={U1,U2,…,Um},由于决策者处于复杂不确定的决策情境中,决策者很难用一个精确数值来表达属性评估值,而倾向于用语言信息对属性指标进行评价,因此,每个方案Ai依据各个属性Uj进行评价,得到的是一个语言信息评价矩阵Z=[zij]n×m,其中zij为语言值,决策的目的是要从备选方案中确定一个最优的方案,或者是对备选方案进行综合排序(如图3所示)。具体决策步骤如下:
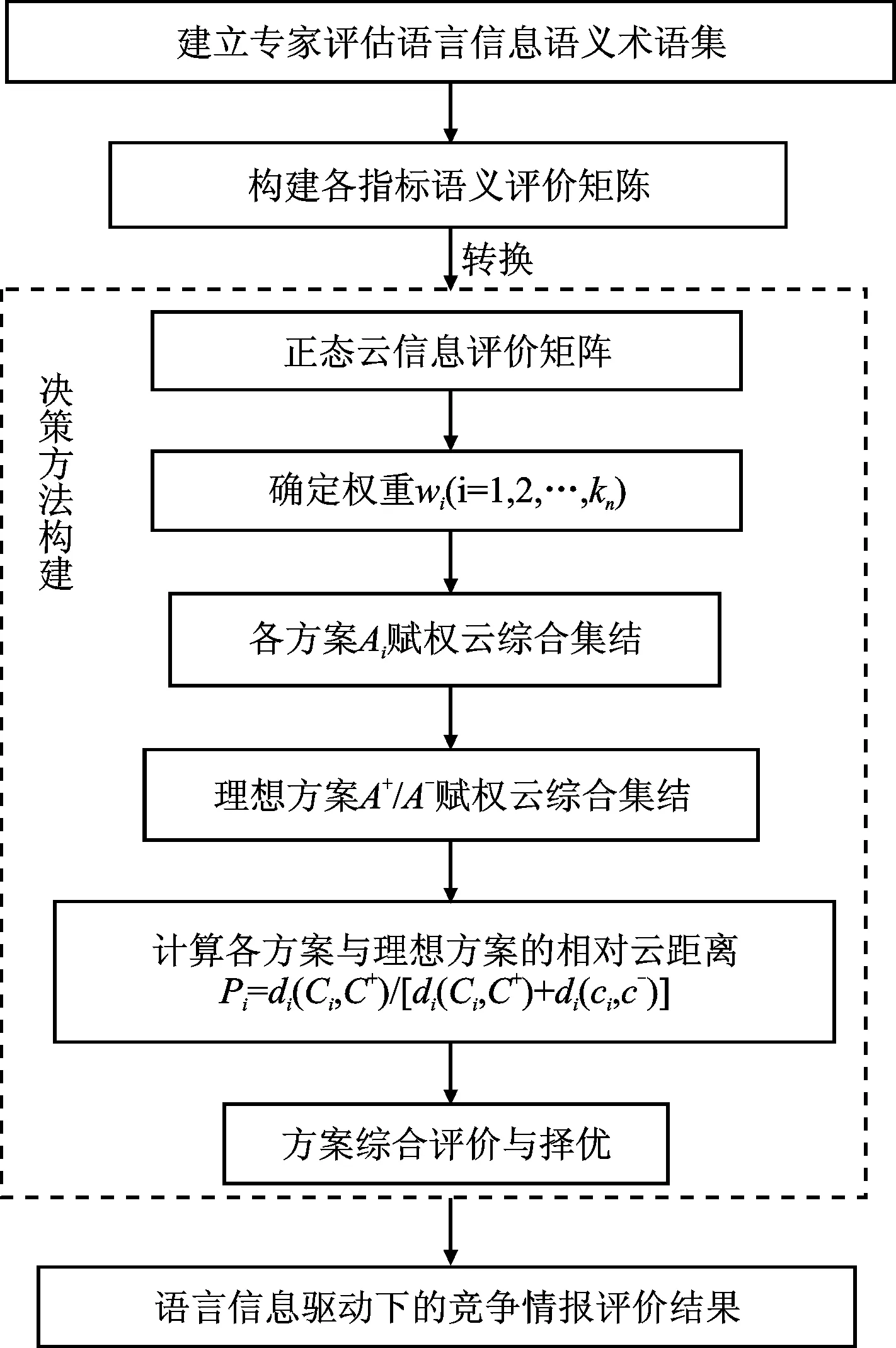
图3 基于云距离的多属性决策流程
步骤1:建立属性指标的语言术语集S={…,S-1,S0,S1,…},例如,7级的语言术语集S:{S-3=非常差,S-2=很差,S-1=差,S0=一般,S1=好,S2=很好,S3=非常好};
步骤2:利用语言变量与云模型的转换公式,将语言信息决策矩阵Z=[zij]n×m转化为正态云模型矩阵H=[hij]n×m,其中hij=Cij(Exij,Enij,Heij)为正态云[13];
步骤3:根据正态云模型矩阵H=[hij]n×m,确定方案Ai在不同属性指标Uj下的正负理想方案A+和A-分别为h+=(maxExi,minEni,minHei)和h-=(minExi,maxEni,maxHei);
步骤4:若已知属性权重信息W={w1,w2,…,wm},则按照云模型的代数运算法则得到n个方案Ai和理想方案A+/A-的加权集结综合云模型分别为:
若属性权重信息完全未知,利用正态云不确定度ρ最小的思想确定客观权重,即属性权重的确定是要使得决策者给出的正态云评价矩阵的不确定度越小越好,则表明决策者的决策越精确,因此可以建立下列目标规划函数:
(10)
通过构造拉格朗日函数方法,得到客观权重值为
(11)
步骤5:利用云加权算术平均(CWAA)算子得到的加权综合云模型,这仍然是一个正态云,不能直接进行比较,因此,利用云Manhattan距离公式(9)计算各方案Ai和理想方案A+/A-之间的加权综合云模型的距离值d(Ci,C+)和d(Ci,C-),并计算相对云距离
(12)
Pi越小则Ai方案越好,计算可得各个方案的排序结果,从而选择最优方案。
(二)实例分析
为了便于比较,本文引用文献[20]的实例,某企业的情报人员收集并整理了A、B、C、D、E、F等6条企业竞争情报,决策者选取情报的商业性(U1)、情报的时效性(U2)、情报的可靠性(U3)和情报的对抗性(U4)等4个指标作为评价指标体系。为了简化计算过程且不失一般性,假定决策者在7级标度的语言术语集S:{S-3=最低,S-2=很低,S-1=低,S0=一般,S1=好,S2=很好,S3=最好}中选择语言变量,并对方案进行评估,6条竞争情报在4个指标下的决策矩阵如表2所示。

表2 竞争情报决策语言信息
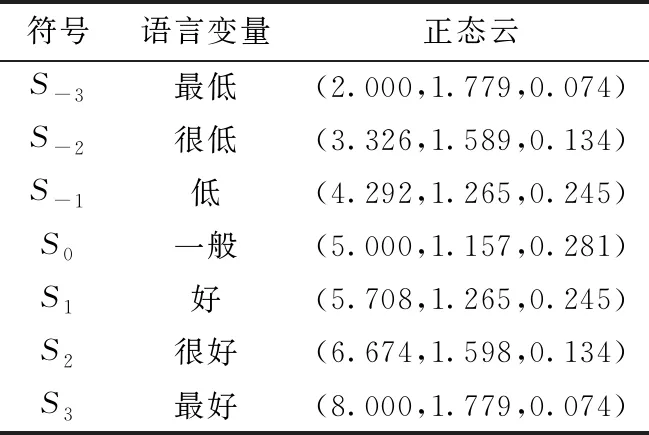
表3 评估语言术语集
首先,假定决策者论域为[Xmin,Xmax]=[2,8],利用语言变量与云的转换模型将语言值转化为正态云模型,得到7级标度的正态云模型,结果如表3所示。根据表3的语言变量和正态云信息转换对应关系,将表2的决策语言信息矩阵转换为正态云信息矩阵,并确定6条企业竞争情报A-F在不同属性指标Uj(j=1,2,3,4)下的正负理想云方案I+和I-,结果如表4所示。

表4 竞争情报决策正态云信息
由于各个指标属性权重信息完全未知,因此,依据正态云不确定度ρ最小的思想,权重的确定是要使得决策者给出的正态云评价矩阵的不确定度越小越好,因此可以建立下列目标规划函数:
minf=0.085 3w1+0.114 7w2+0.159 5w3+0.124 7w4
通过构造拉格朗日函数方法,计算上述目标规划可得归一化权重值为
w1=0.211 5,w2=0.226 7,w3=0.315 2,w4=0.246 5
将表4的正态云决策矩阵和权重值进行CWAA算子集成,得到竞争情报的加权综合云评估值(如图4所示):

图4 竞争情报方案加权综合云模型
CA=(5.149 2,0.595 6,1.065 4)
CB=(5.160 0,0.597 0,1.213 7)
CC=(4.820 0,0.641 9,1.064 8)
CD=(5.737 2,0.660 9,1.213 0)
CE=(5.553 5,0.649 1,1.415 9)
CF=(5.605 7,0.696 2,0.914 4)
相应的正负理想方案的加权综合云评估值为:
CI+=(6.368 8,0.585 7,1.414 4)
CI-=(4.484 9,0.748 1,0.916 9)
由于上述竞争情报的综合云模型不是一个常数,无法直接进行比较,因此,通过云Manhattan距离度量式(9)计算各竞争情报与正负理想方案之间的距离值d(*,I+)和d(*,I-)进行比较,结果如表5所示。

表5 竞争情报与理想方案之间的云距离
最后,根据式(12)得到6个竞争情报的相对距离为P=(0.640 6,0.616 1,0.803 3 0.343 8,0.411 0,0.449 1),根据排序向量值的大小,企业竞争情报的排序为D>E>F>B>A>C,最佳竞争情报为D。
为进一步检验基于云Manhattan距离的语言型多属性决策方法的合理性与有效性,对上述案例选取文献[10]的Hamming距离方法和文献[17]的Euclidean距离方法与本文方法进行竞争情报方案排序,得到的排序结果如表6所示。由表6可知,Euclidean距离方法与本文方法的排序结果是一致的,但是Manhattan距离方法更稳定,尤其是在超熵相差比较大的情况下。Hamming距离方法的效果最差,最优方案B与实际情况不符,主要是由于熵和超熵只是作为期望的权重,弱化了两者的作用,导致结果偏差较大。

表6 不同距离方法的排序结果比较
五、结 论
云模型作为一种全新的双向认知模型,用期望、熵和超熵三个数字特征建立了定性概念和定量数值之间沟通的桥梁。本文基于云模型对属性完全未知且属性值为语言变量的多属性决策问题进行了研究,分别提出了云不确定度和云Manhattan距离,并在此基础上提出了一种基于云不确定度最小的客观权重确定方法,构建了一种基于云期望方差Manhattan距离的多属性决策方法。企业竞争情报决策实例表明,所提出的方法具有较好的操作性,是对不确定多属性决策理论和方法的进一步探索和完善。本文的期望方差Manhattan距离度量方法主要是从正态云期望曲线和含熵期望曲线的期望和方差角度出发,且主要应用于属性权重完全未知的语言型多属性决策,在今后的研究中,可以考虑对不同的距离度量方法和权重信息不完全的语言型多属性决策进行研究。

