随风潜入夜 润物细无声——对2021年赣州市期末考试第12题的拓展

江西省赣州中学 (341001) 廖志勇

数学家波利亚指出:“拿一个有意义但不复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题就像通过一道门户，把学生引入到一个完整的数学领域.”从一个基础问题出发，探寻问题本质并拓展延伸，培养学生思维能力，鼓励学生独立思考，逐步学会探究性学习解决新的数学问题.

一、问题提出及求解

(2021年期末考试理科12题)过抛物线y2=4x的焦点，做两条相互垂直的弦AB,CD,且|AB|+|CD|=λ|AB||CD|，则λ的值为( ).

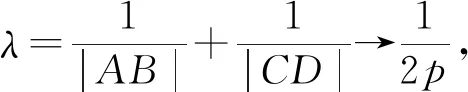
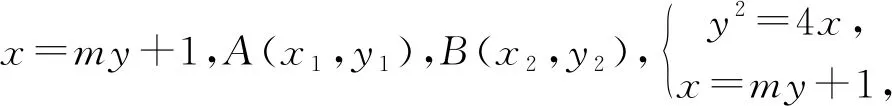
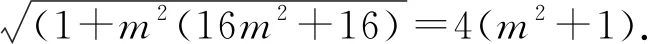
二、问题探究

既然抛物线有这个结论，那么我们是否推广到其他圆锥曲线，我们提出问题：

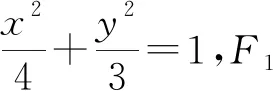
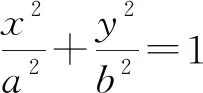
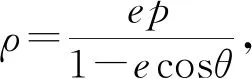
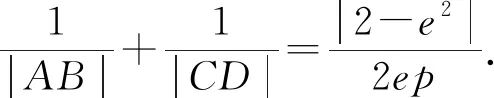
三、问题引申

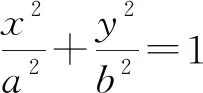
例题过抛物线y2=4x的焦点做两条互相垂直的弦AB和CD，求四边形ABCD的最小值.

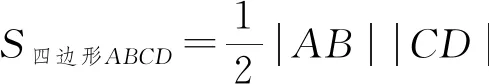
类似的，对椭圆和双曲线，我们可以提出从抛物线延伸到其他圆锥曲线，得到类似的结论.问题不同，却是相同的处理和相似的解题思路.

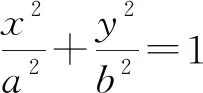
证明：设直线x=my-c，M(xM,yM),联立方程

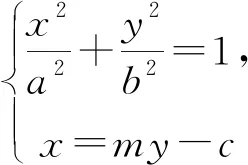
四、反思总结

从一个简单的问题出发，拓展延伸学生的思维能力，渗透核心数学素养，关键是培养学生理解问题，解决问题的能力.数学有着有趣的灵魂，它的思维、简洁之美都是学习数学的一种快乐，而能从一些问题中探寻或寻找问题的本质，潜移默化转成自己的思维能力和品质，也是学习数学的一种快乐.