赏析一道新高考压轴题及其解法

廖永福 林永志

(1.福建省厦门第二中学 361009；2.福建省仙游县榜头于洁小学 351256)

这是2020年山东省新高考数学填空压轴题，也是一道立体几何中的轨迹问题.题目简短无图，中规中矩，但包含的信息量较大，考查的知识点较多.平淡中还暗藏玄机，有一定的难度，属中档题.

本题考查直棱柱的结构特征、直线与平面垂直的判定和性质、扇形的弧长公式；考查作图和计算能力、推理论证和空间想象能力；考查数形结合思想、化归转化思想、函数与方程思想等.

解答此题除了必要的知识储备外，正确作图、准确理解题意也是重要的一环，有些考生把球面与侧面BCC1B1的交线误解成球面与平面BCC1B1的交线，结果前功尽弃.下面给出这道题的四种解法，希望能够起到抛砖引玉的作用.

解法一利用圆的定义解题

图1

如图，设E、F、G分别是棱B1C1、BB1、CC1的中点，连结D1E、EF、EG.

又四棱柱ABCD﹣A1B1C1D1为直四棱柱，所以BB1⊥平面A1B1C1D1，所以BB1⊥D1E.

因为BB1∩B1C1=B1，所以D1E⊥侧面BCC1B1.

设P为球面与侧面BCC1B1交线上的任一点，连结D1P、EP，则D1E⊥EP.

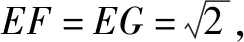
因为∠B1EF=∠C1EG=450，所以∠FEG=900.

解法二利用球的截面的性质解题

图2 图3

解法三通过建立平面直角坐标系解题

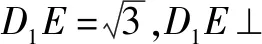
图4 图5

如图建立平面直角坐标系，则E(1,2)，设P(x,y)为球面与平面BCC1B1交线上的任一点，连结D1P、EP，易得D1E⊥EP，所以|D1E|2+|EP|2=|D1P|2.

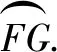
解法四利用向量的性质解题

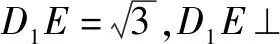
图6 图7

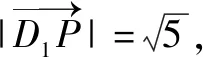
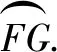
解法二紧扣球的截面的性质，首先明确球面与平面BCC1B1的交线是球的小圆，小圆圆心是球心D1在平面BCC1B1内的射影，即棱B1C1的中点E，根据小圆半径、球半径以及面心距之间的关系，求出小圆半径，进而解决问题. 此法大道至简、大巧若拙，是最本质的一种解法.

解法三通过建立平面直角坐标系，根据球面与平面BCC1B1交线上的点所应满足的等量关系，求出交线的方程，进而解决问题，这是几何问题代数化常用的一种方法.

解法四巧妙地引进向量，利用向量模的性质得到球面与平面BCC1B1交线的方程，此法算是博采了代数和几何的精华，过程简洁明了、曲径通幽．

上述四种解法各有千秋，又联系紧密，它们都是解决立体几何轨迹问题的常用方法.可以看出，解答这类问题的关键是要善于把空间问题转化为平面问题，再利用平面几何、解析几何以及空间向量等知识求解.