数列综合问题的题型及其解法

刘 成

(江苏省苏州实验中学 215000)

一、与不等式相关的数列综合问题

数列和不等式的综合性问题，一般都会用求最值的形式对学生进行考察.解答这类问题首先要处理Sn和an之间的关系式，根据题意考虑是将Sn往an转化，如Sn-Sn-1=an，还是把an向Sn转化，如a1+…+an=Sn；其次还要学会求解不等式，通过求解不等式求出最后答案.如例1所示.

例1设Sn是数列{an}的前n项和，且a1=3，当n≥2时，有Sn+Sn-1-2SnSn-1=2nan，则使得S1S2…Sm≥2019成立的正整数m的最小值为____.

解∵Sn+Sn-1-2SnSn-1=2nan(n≥2)，

∴Sn+Sn-1-2SnSn-1=2n(Sn-Sn-1)(n≥2)，

∴(2n+1)Sn-1-(2n-1)Sn=2SnSn-1(n≥2)，

∴数列{bn}是以1为首项，2为公差的等差数列，bn=2n-1，

∴m≥1009.

思考该题求参数m的最值，是一道既考察不等式又考察数列的综合性问题.其中所解不等式含有参量Sn，首先要找到Sn与an之间的转化关系，再对问题中的不等式进行求解，即可求到最终答案.

二、与三角函数相关的数列综合问题

数列和三角函数相互交汇的综合性问题并不少见，解答该类型问题首先是灵活运用正余弦定理，得到三角形中边角的关系，其次是对数列公式的巧妙运用，如等差数列通项公式an=a1+(n-1)d，最后针对求解得到的数列通项特点，运用裂项相消、分组求和等方法求解综合问题，从而得到最后答案.如例2所示.

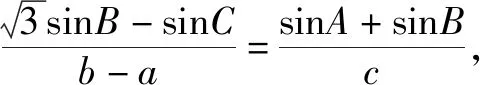
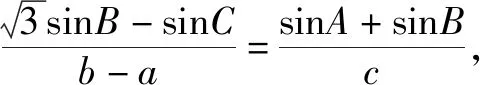
∵a1sinA=1，

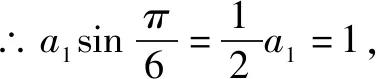
∵a2,a4,a8是等比数列，

∴d2=2d，

∵d≠0，∴d=2，数列an=2n，

三、与函数相关的数列综合问题

数列和函数交叉综合出题，既可以对函数相关知识点进行考察，也可以对数列有关知识进行考核.解答该类综合问题时，首先根据问题利用相对应的函数知识点求解，得到其中的an或Sn，如求函数极值点，则对函数进行求导得f′(x)，令f′(x)=0可知其函数极值点，其次对数列进行整合，通常会借助函数求数列的通项或前n项和，具体解题步骤如例3所示.

通过上述三种不同解题方法，同学们可以更加全面地了解如何求解数列求和问题，倒序相加、错位相减、裂项相消都能够有效解答数列求和问题.因此同学们应该善于从平常试题中发现并总结方法，明确解题思路的方向，从而提升解题效率.