从一道模拟题的多解谈解三角形的一轮复习
洪汪宝
(安徽省安庆市第一中学 246004)
题目已知△ABC中,角A,B,C的对边分别为a,b,c,且2sinAcosB-sinBcosC=sinCcosB.
(1)若a,b,c成等比数列,试判断△ABC的形状;
(2)若a=2,c=3,点D在边AC上,且BD平分∠ABC,求BD的长.
本题是我校2020届高三第三次模拟考试的理科第17题,主要考查三角恒等变换、特殊角的三角函数值、等比数列的定义、正弦定理、余弦定理等多个知识点,对学生的逻辑推理能力和运算求解能力要求较高,要求学生具备扎实的逻辑推理素养和数学运算素养.
一、解法探究
1.第(1)小题的解法
由a,b,c成等比数列知b2=ac.
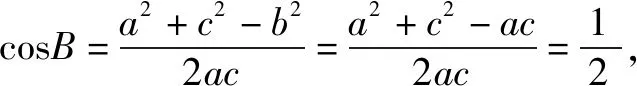
方法2由余弦定理知b2=a2+c2-2accosB=a2+c2-ac≥2ac-ac=ac,当且仅当a=c时,b2=ac,因此△ABC是等边三角形.
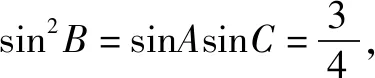
点评解法1直接利用余弦定理并整理得到完全平方式;解法2利用重要不等式,巧用取等条件,将解三角形与重要不等式相结合,是我们常见的一个综合点;解法3发现所给等式的两边均为二次,利用正弦定理,将边化为角,再利用三角恒等变换,对学生的运算求解能力要求较高;解法4引入公比q,实际上是为了消元,将多元化为一元,体现了转化与化归思想.
2.第(2)小题的解法


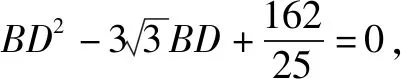




点评解法1,2,3主要都是利用正弦定理和余弦定理,思路比较自然.根据已知条件,在△ABC中,已知两边及其夹角,该三角形是唯一确定的,所以其内角平分线的长也是唯一的.解法1中出现两解,要注意取舍,而且整个计算过程比较繁琐,不少学生应用了该解法,但算出来的不多;解法2的后面利用了正弦定理,效果比较好;解法3挖掘出隐藏条件∠ADB+∠CDB=π,要注意这个模型的应用.



二、复习建议
1.理清知识要点,正确选用定理
解三角形是每年高考的必考知识点,我们在复习过程中必须理清知识要点,弄清知识要点的来龙去脉.比如说正弦定理,我们知道它反映了同一三角形的边角之间的等量关系,在一轮复习中可以设计如下的问题链:
(1)正弦定理的具体内容是什么?(文字语言、图形语言、符号语言等)
(2)如何证明正弦定理?常见证法有哪些?(作高、面积法、作外接圆、向量法等)

(4)何时利用正弦定理来解三角形?(已知两角与一边,已知两边与其中一边的对角)
(5)利用已知的两边与其中一边的对角解三角形时,要注意什么?
2.开展一题多解,促进深度学习
考试或作业时因时间有限,大部分学生解完题目就认为万事大吉了,没时间进一步思考,制约了学生的思维质量与思维层次,不利于学生思维的培养.于是要求老师在批阅试卷和作业时要注意搜集典型题目和解法,笔者在初次见到上面的题目时,感觉很平常的一道问题,但在批阅试卷时,惊喜连连,上面提供的解法基本上都是学生考试中运用的方法,只不过有的解法学生用的比较多,有的用的比较少.
3.精心组织微专题,提升复习效率
在一轮复习过程中,大部分老师都喜欢直接利用一轮复习用书,按照书上的要求进行讲解,没有自己的再加工,长此以往,学生对复习必将失去兴趣,影响复习效果.微专题教学是时下比较流行的教学方式,特别在复习课中应用比较广泛,微专题具有切口小、选题精、角度新、针对性强等特点,这样可有效抓住热点,突出重点,突破难点和易错点,从而备受广大一线教师的青睐.所以要求老师精心挑选组织微专题,微专题的选择要“微”在定点突破,“微”在精心预设,“微”在互动生成.

