基于神经网络逼近的磁浮列车动态悬浮控制

王 强

(中国铁建电气化局集团第四工程有限公司, 长沙 410007)

为了能满足人们在有限资源下对于高速且大容量交通工具的需求，磁浮列车这一种依靠悬浮特性实现无接触运行的交通工具作为一项重点研究计划具有一定的前瞻性。而如何实现列车的稳定悬浮并且能够在外部扰动作用下具有较好的控制精度和抗干扰性是保证稳定运行的核心之一[1-3]。因此在这一大背景下，很多专家和学者针对悬浮控制算法以及车轨耦合振动机理进行了大量研究，并且取得了很多有价值的研究成果。

随着研究的逐步深入，列车的静态悬浮状态已经达到了一个较为成熟的地步，悬浮状态下磁轨之间的耦合振动问题已经得到了逐步解决。但如何能保证磁浮列车在动态激励下依旧能够在最大程度上保持悬浮稳定性是限制磁浮列车工程化应用的核心问题之一。张鋆豪等[4]研究了悬浮系统的线性自抗扰控制问题，并且证明了线性自抗扰控制在响应快速性以及抑制外部扰动等方面均优于比例-积分-微分(proportion-integral-derivative, PID)控制器。董达善等[5]建立了悬浮系统的非线性动力学模型。设计了相关的模糊控制算法初步克服外界干扰。佟来生等[6]提出了一种基于二类李雅普诺夫函数的滑模控制策略使其能够严格保证系统维持在目标悬浮间隙附近。通过对比仿真验证所提出控制律的有效性和鲁棒性。王军晓等[7]提出了一种基于等价输入干扰滑模观测器的模型预测控制方法。结果表明，所提方法提高了磁悬浮球系统的跟踪性能，并且初步抑制了系统不确定性和外部干扰。王树宏等[8]针对磁浮列车悬浮间隙变化速度无法测量的问题提出一种基于扩张状态观测器(extended state observer, ESO)的反演控制方法，并基于对称Barrier Lyapunov函数证明了该方法的稳定性。分析可知，一些实际问题如轨道柔性变形导致的不平顺扰动以及负载变化引起的悬浮力突变等并未进行有效分析。而在实际运行中，由于乘客流动、轨道刚度不足、高架支撑梁沉降等现象的存在，外部扰动是不可避免的，这可能会使系统发生耦合振动，甚至引发“打轨”等不稳定现象。其中，轨道不平顺则是当前影响悬浮性能的最主要因素之一。因此，设计合适的控制方法来克服不平顺扰动具有一定的实际意义。Tran等[9]提出了一种任意有限时间跟踪控制方法。通过引入一种新的增广滑模流形函数，消除了传统终端滑模控制中的奇异性问题和到达相位问题。通过对实际磁悬浮系统的仿真和实验研究，验证了所提方法的有效性。张文跃等[10]考虑了悬浮系统的本征非线性特征，利用反步法对系统进行分离，并分别提出Lyapunov候选函数，并证明了系统的稳定性。李琴等[11]采用径向基函数(radial basis function,RBF)神经网络PID控制结合的方法来对四旋翼飞行器的姿态跟踪进行控制，结果显示，所提出算法比普通PID控制的跟踪能力更好。

在对当前磁浮列车和控制算法的研究前沿进行充分分析和总结的基础上，以单点悬浮模型为基础结合RBF神经网络和Lyapunov稳定性分析设计了相关的自适应RBF神经网络控制算法，相比一般的梯度下降法调节网络权值更能保证闭环稳定而不陷入局部最优，并且通过数值仿真基于不同工况验证了所提出算法的有效性，并在最后基于半实物仿真平台进行了相关的实验验证。

1 单点悬浮系统模型

1.1 模型描述

图1给出了所采用的单点悬浮控制系统结构图，该系统主要由轨道、电磁铁、负载、传感器、悬浮控制单元构成。

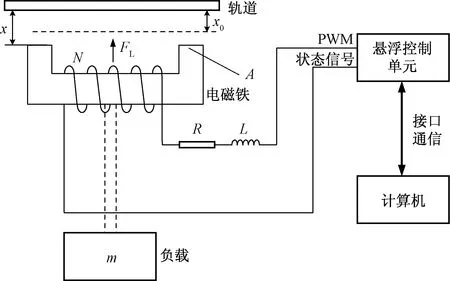
x0为平衡点位置悬浮间隙；x为悬浮间隙； A为电磁铁磁极面积；FL为电磁力； R和L分别为电磁铁绕组自身电阻和电感； N为线圈匝数；m为质量负载； PWM(pulse width modulation)为脉冲宽度调制图1 单点悬浮控制系统结构Fig.1 Structure of single point levitation control system

结合以往研究可以给出电磁铁及负载在竖直方向上的力学方程和电压方程为

(1)

式(1)中：μ0为真空磁导率；x为悬浮间隙；u为控制电压；i为线圈电流；g为重力加速度；A为电磁铁磁极面积；t为时间。

(2)

对其进行线性化可以得到以悬浮间隙为输出、控制电压为输入的传递函数模型为[12]

(3)

式(3)中：Δx为悬浮间隙误差；Δu为调整电压误差；s为拉氏空间的变量符号，无特殊含义。

进一步提取系统特征方程为

(4)

根据劳斯判据，式(3)所示线性模型三阶不稳定，因此可知，图1所示单点悬浮系统同样三阶不稳定，必须设计恰当的反馈控制律才能实现稳定悬浮。

2 控制算法设计

2.1 控制器设计

定义稳定悬浮后的参考悬浮间隙为x0，通过图1可得实际悬浮间隙为x，则动态误差e及误差矩阵E可分别表示为

(5)

采用图2所示的2-5-1网络结构构造控制模型。

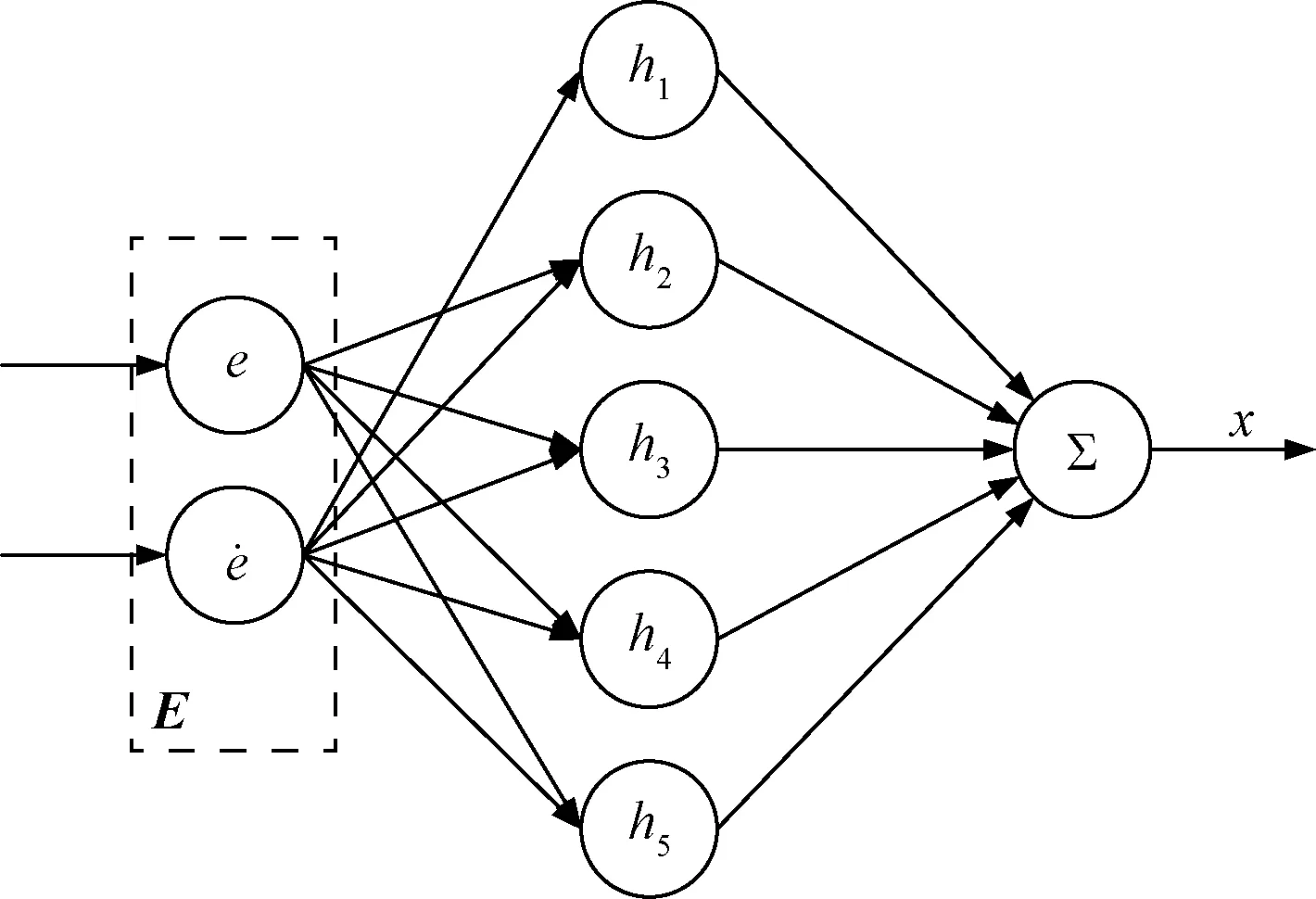
图2 2-5-1径向基函数网络结构Fig.2 2-5-1 radial basis function network structure

其中输入为误差矩阵，网络的隐含层输出矩阵为h=[h1h2h3h4h5]T，第j(j=1,2，…,5)个神经元的输出和对应的高斯基函数中心点的坐标向量为

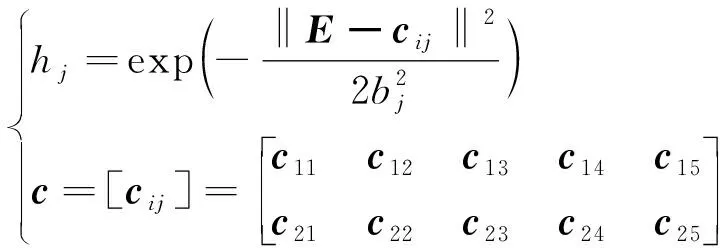
(6)

式(6)中:bj表示第j个神经元高斯基函数的向量宽度；i=1,2；hj为第j个神经元的输出，j=1,2,…,5；c为对应的高斯基函数中心点的坐标向量；cij为第i个输入到第j个神经元高斯基函数中心点的坐标向量。

x(t)=wTh=w1h1+w2h2+…+w5h5

(7)

对式(2)中的方程(3)进行分析可表示为

(8)

从式(8)可以看出，f(z1,z2,z3) 中各个状态变量存在互相耦合，不满足线性关系，因此同样可以采用径向基网络进行逼近，可表示为

(9)

闭环控制框图如图3所示。

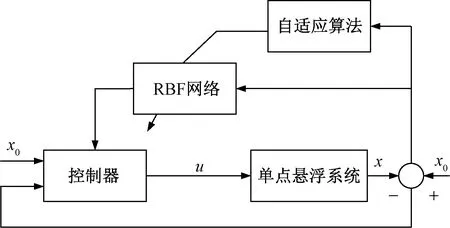
图3 闭环径向基网络控制系统Fig.3 Closed loop radial basis function network control system

采用式(9)所示逼近输入代替式(2)和式(8)中所示f(z1,z2,z3)，可以得到相关的控制律为

(10)

(11)

2.2 稳定性分析

(12)

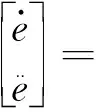
(13)

从而得到最优权值为

(14)

式(14)中：sup为函数上界。

(15)

结合式(14)对式(13)进行进一步推导得

(16)

定义Lyapunov函数为

(17)

式(17)中：γ为正常数，可在仿真调试中采用试凑法获得，且P必定满足式(18)。

HTP+PH-Q=0

(18)

式(18)中：Q为由P矩阵唯一确定的正定对称矩阵。

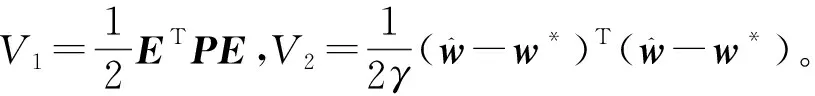
对V1进行求导得

(19)

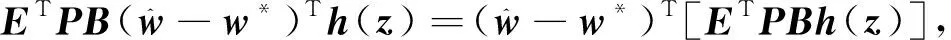
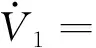
(20)

对V2进行求导得

(21)

因此可得

(22)

代入式(11)所示自适应律，可得

(23)

3 数值仿真

3.1 仿真框架及参数定义

为进一步说明算法的有效性，基于MATLAB/Simulink仿真平台对算法进行仿真验证，构造单点悬浮仿真框架如图4所示。

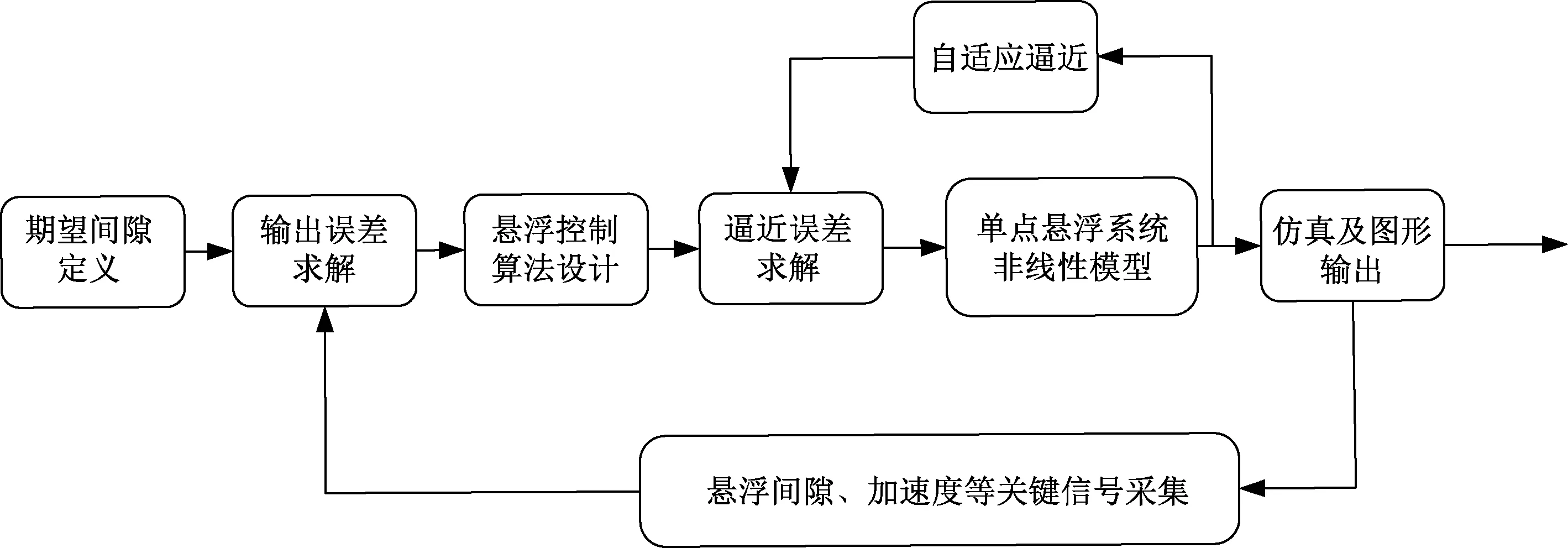
图4 单点悬浮控制仿真框架Fig.4 Simulation framework of single point suspension control

采用单点悬浮控制系统参数如表1所示。为了验证本文所提出算法的有效性和先进性，从初始悬浮响应速度、稳态误差以及抗干扰性三个方面与现有PID控制进行综合对比。由于缺乏试验数据，无法基于实测数据验证算法的跟踪性能，因此首先基于正弦函数验证算法的跟踪性能。其次，对模型分别施加图5、图6所示负载扰动力和不平顺激励对算法的抗干扰性进行分析。

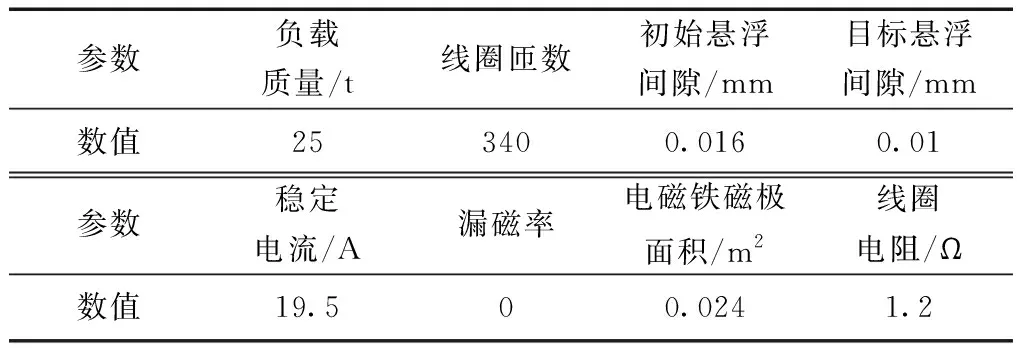
表1 单点悬浮控制系统参数Table 1 Parameters of single point suspension control system

图5 负载扰动力Fig.5 Load disturbance

图6 不平顺扰动激励Fig.6 Disturbance excitation of irregularity

3.2 仿真结果分析

3.2.1 正弦信号跟踪

在分析过程中，首先采用幅值为±0.005 m的正弦信号作为期望跟踪信号进行跟踪性能仿真，从图7可以看出，传统PID控制算法的控制性能较弱，并且存在一定误差，最大偏差达到1 mm，不利于信号跟踪。相比之下，径向基网络控制下系统输出能够更好地逼近期望信号，毕竟误差小，最大误差仅为0.47 mm。

图7 系统动态跟踪性能对比验证Fig.7 Comparison and verification of system dynamic tracking performance

3.2.2 负载力扰动

根据图8可以看出，在起始悬浮阶段，径向基网络能够使系统具有更快的响应速度而不产生超调量，通过不断调试可以发现系统在PID控制的作用下进一步提高响应速度则会产生较大超调量，不利于系统稳定性。此外，在大负载扰动的作用下，虽然径向基网络和PID控制均能具有较好的稳定输出，但是从图8中仍旧可以看出径向基网络控制下的系统输出偏差更小。

图8 负载扰动下输出悬浮间隙Fig.8 Output suspension gap under load disturbance

3.2.3 不平顺激励扰动

从图9可以看出，在系统稳定之后，在5 s施加图6所示不平顺激励，系统在PID控制下输出突变较大，达到0.8 mm；此后，由于不平顺激励的持续作用，系统虽然并未发散，但始终处于微小振颤状态，不利于悬浮稳定性。而在径向基网络的作用下，5 s时的突变幅值明显减小，仅为0.2 mm，并且振颤情况得以明显改善。说明了该算法能够使系统在具有较快响应速度的同时具备更好的抗干扰性。

图9 不平顺激励下输出悬浮间隙Fig.9 Output suspension gap under irregularity excitation

4 实验验证

通过单点悬浮试验台对所提出RBF神经网络控制算法进行初步验证，实验平台如图10所示。

图10 实验平台Fig.10 Experimental platform

在实验过程中定义期望悬浮间隙为8 mm，稳定悬浮电流为26.5A。算法基于Dspace半实物仿真平台编译。系统所输出悬浮间隙和控制电流分别如图11、图12所示。可以看出，RBF网络控制下的悬浮间隙具有更小的超调量，并且稳态误差趋近于0，而在PID控制下，系统输出在起浮阶段具有明显的波动过程，调节时间慢且超调量大。在稳定悬浮之后，系统具有一定的稳态误差，进一步证明了本文所提出算法的有效性。

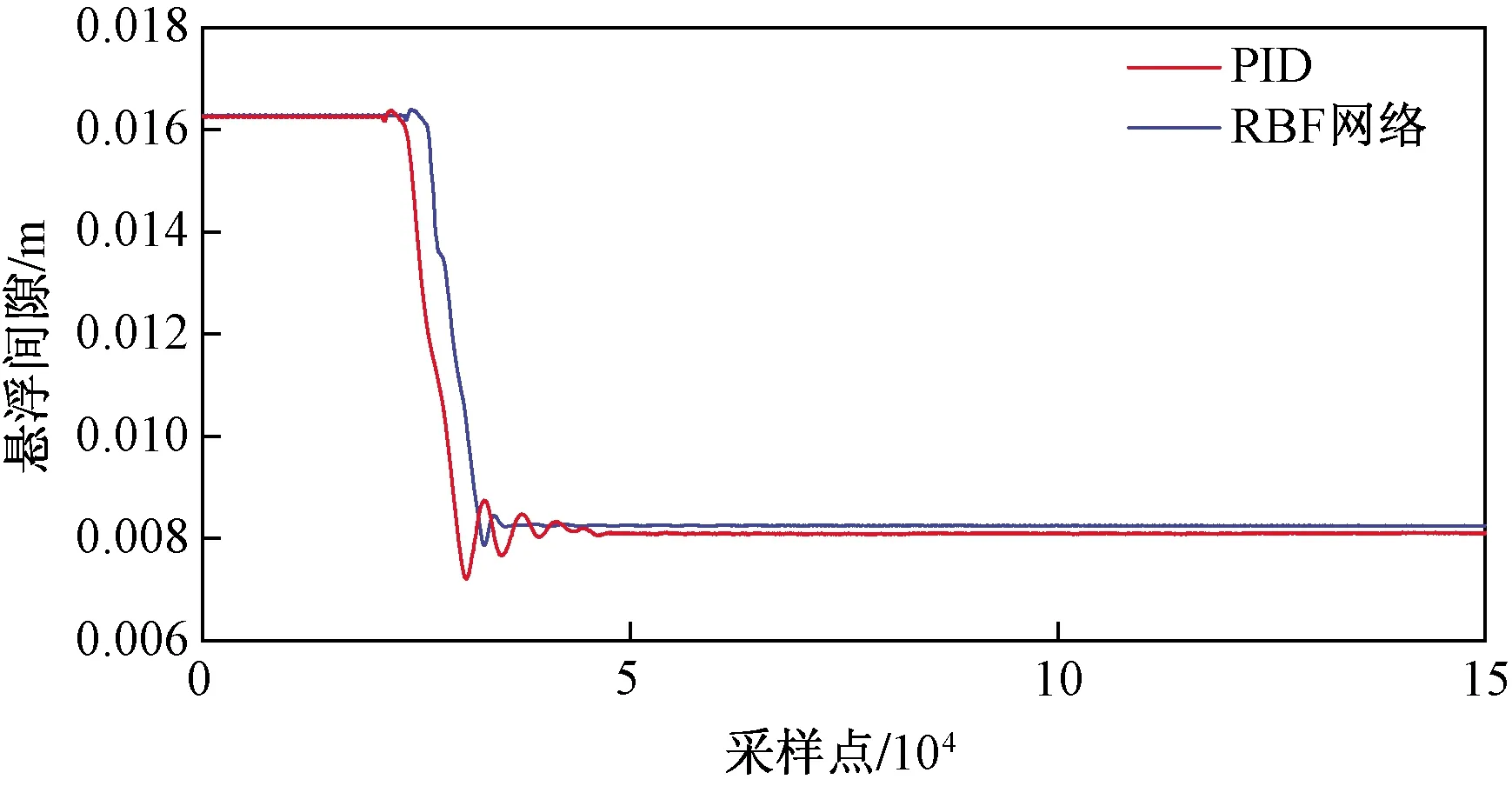
图11 悬浮间隙Fig.11 Suspension gap

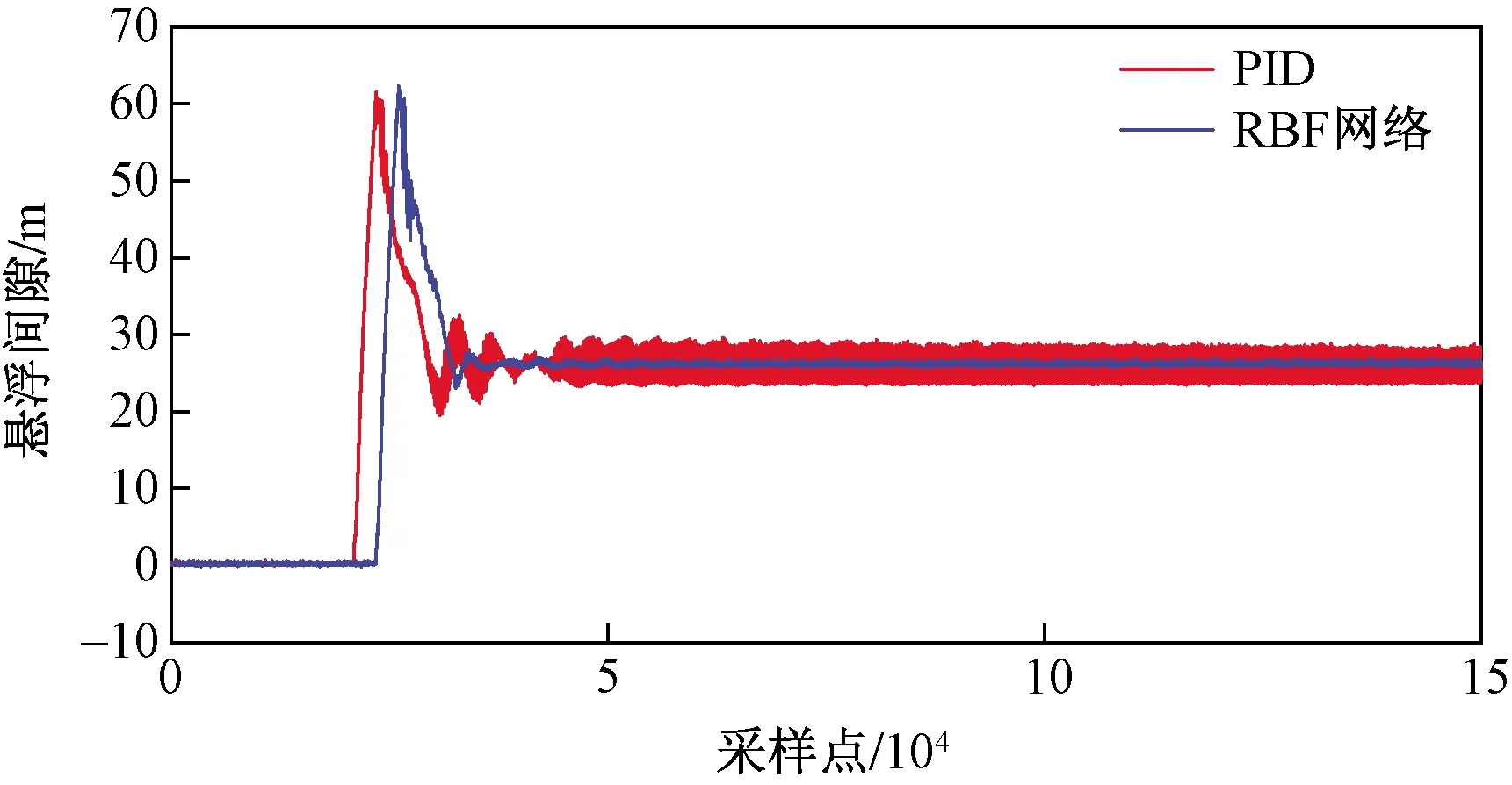
图12 控制电流Fig.12 Control Current

5 结论

磁浮列车在运行过程中，由于轨道梁挠度变形和负载激励都会导致悬浮力的变化，因此外界动态扰动极大地考验了悬浮控制系统的抗干扰性和动态性能，由于运行过程中的稳定悬浮间隙仅为10 mm，任何一种扰动导致间隙变化都极易影响列车的悬浮状态，因此如何在有界小约束可调区间内对悬浮间隙进行动态调整对于保证稳定性而言至关重要。基于单点悬浮系统进行了相应的系统建模和控制算法设计，得到如下结论。

(1)首先以电压控制思路构造了单点悬浮控制系统的相关数学模型，并通过特征方程和劳斯判据说明了悬浮系统具有本征非线性的特性并且开环不稳定。

(2)确定了单点悬浮系统控制算法所需要的径向基神经网络基本结构，基于悬浮间隙误差设计控制律和自适应律并采用Lyapunov函数确定了其闭环稳定性。

(3)以幅值为±0.005 m的正弦函数为例，对本文所设计径向基网络算法的跟踪性能进行了相应验证，并且与当前应用较为广泛的PID控制算法进行对比，可以看出所提出控制算法具有更好的跟踪性能。

(4)通过数值仿真和实验分别说明了在负载扰动下和不平顺激励扰动下的输出情况。根据响应速度、稳态误差以及抗干扰三个方面的综合对比可以看出，本文算法能够更好的应对列车运行过程中的动态扰动，从而提高系统稳定性来实际解决列车运行过程中的共振以及掉点现象。