汾渭平原SO2与气温的函数型空间自回归分析
胡锡健, 李妍琳, 石小平
(新疆大学数学与系统科学学院, 乌鲁木齐 830046)
在中国经济由高速增长阶段转向高质量发展阶段过程中,环境治理和污染防治是一道重要关口。近年来,推进大气污染防治工作卓有成效,京津冀地区空气质量显著提升,长三角、珠三角地区空气质量持续达标,汾渭平原却成为中国空气污染最严重的区域之一,引起国家和社会的高度重视[1]。2018年7月,在《打赢蓝天保卫战三年行动计划》中,汾渭平原被纳入环境污染三大重点防控区域之一,成为蓝天保卫战的“主战场”。
汾渭平原能源结构以煤为主,煤炭在能源消费中占约90%,远高于全国平均水平(60%),煤烟型污染特征明显,大气中的主要污染物有二氧化硫、二氧化氮、可吸入颗粒物等,这不仅对健康带来了很大的危害,还影响着人们的正常生活。
大气污染状况与当地的气象条件有着密切的关系。缪明榕等[2]分析了南通市2018年大气污染物与气象因素的关系。张岳军等[3]、张连华等[4]分别对汾渭平原SO2和NO2进行时空分布特征分析,研究该区域的SO2、NO2的污染状况,全面了解汾渭平原SO2、NO2的时空变化特征,对有效治理大气污染具有重要意义。
气象数据在时间尺度上有明显的函数特征,汾渭平原11个城市的逐时气温数据一年有9万多条,面对如此庞大的数据集,传统的数据分析方法不能对这些数据直接处理。函数型数据分析(functional data analysis,FDA)方法专门针对此类数据,采用平滑方法将其拟合成曲线再进行分析。Ramsay[5]于1982年率先提出一种全新的数据分析思路——函数型数据分析;Ramsay等[6]对函数型数据做了进一步详细的描述并讲述了诸多关于FDA的应用。与传统方法相比,函数型数据分析方法不仅在处理高维观测数据上能给出更加合理的直观解释,而且在分析数据时能保留更多的数据信息,从而得到更精确的分析结果。因此,FDA应用于许多学科领域,如生物学、医学、气象学、计量经济学、金融、化学计量学和地球物理学等[7-8]。函数型回归分析是FDA最重要的应用之一,经典函数型线性回归模型(functional linear model,FLM)是函数型线性回归的最简单形式。Paganoni等[9]给出了概述,在FDA研究领域受到广泛关注。在对FLM进行参数估计时;Cardot等[10]首次研究函数型线性回归模型,利用函数型主成分分析方法给出斜率函数估计的收敛速度;Hall等[11]基于函数型主成分分析方法和最小二乘估计方法给出函数型线性回归模型的估计。在做FLM分析时假设所有个体都是相互独立的,但是在信息技术的飞速发展今天,区域之间的相关性信息逐渐显现,具有空间结构的数据越来越普遍。在这些数据中,响应变量由于空间结构而存在较强的相关性,如果使用FLM来分析带有空间相关性的数据,可能无法充分利用数据中包含的信息。当协变量为标量时,通常使用空间自回归(spatial autoregression,SAR)模型来拟合这类具有空间相关性的数据。SAR模型是处理空间相关问题的一种有效方法。
Cliff等[12]在空间自回归的一般模型、参数估计和假设检验方面有了开拓性的进展;Anselin[13]提出了空间自回归的一般模型。近年来,SAR模型的应用越来越广泛;Kanaroglou等[14]将SAR模型用于估计SO2的空气污染浓度.在环境学领域与气象学领域中,观测数据会有曲线形式。因此,将SAR模型的数据类型扩展到函数型数据越来越迫切。Ahmed[15]首次提出了函数型空间自回归模型(functional spatial autoregressive model,FSAR),并利用极大似然估计方法对FSAR模型进行估计,并证明了该模型中参数的渐进性质;Huang等[16]通过借鉴SAR模型的概念,利用空间相关系数和权重矩阵将具有空间结构的数据融入FLM模型中,称该模型为空间函数型线性模型(spatial functional linear model,SFLM),并利用该模型分析了2005—2007年中国34个主要城市年均降水量与月均温度的关系;应彩云[17]将函数型变量引入一般的SAR模型中,构建半泛函SAR模型,并研究相应的参数估计方法。汾渭平原作为中国的四大平原之一,有着严重的大气污染问题,但目前还没有学者函数型回归模型分析该区域的空气质量数据与气象数据之间的关系。从汾渭平原11个城市的空间分布来看,空气质量数据中必然有部分数据存在空间相关性,结合SAR和FLM分析方法,采用FSAR模型探讨该地区空气质量与气象的关系不仅能充分利用数据的空间自相关和高维连续性特征,而且提供分析汾渭平原大气污染情况的新途径。
采用2019年汾渭平原11个城市的空气质量数据[PM2.5、PM10.0、SO2、NO2、O3和CO的监测数据及空气质量指数(air quality index,AQI)],运用空间自相关Moran’sI检验对这7项数据做空间自相关分析,选择检验结果最显著指标作为响应变量,并采用2019年该区域11个城市的逐小时气温,应用函数型空间自回归方法构建空气质量数据与气温的FSAR模型。定量分析汾渭平原11个城市空气质量数据与气温的相关性,并与普通的函数型回归模型进行比较分析。
1 数据说明与方法
1.1 研究数据
选取汾渭平原(包括河南省洛阳市、三门峡市,陕西省西安市、咸阳市、宝鸡市、铜川市、渭南市,山西省吕梁市、晋中市、临汾市、运城市) 11 个市作为研究对象, 整理了2019年汾渭平原地区11个城市的7项空气质量数据[PM2.5、PM10.0、SO2、NO2、O3和CO的监测数据及空气质量指数(AQI)]和气象数据(地表气温),数据分别来自中国空气质量在线监测分析平台和美国国家航空航天局MERRA2中的inst1_2d_asm_Nx文件集。汾渭平原11个城市在空间上的分布如图1所示。

图1 汾渭平原地形图Fig.1 Topographic map of Fenwei plain
1.2 函数型空间自回归模型
FSAR的一般形式为
(1)
式(1)中:x(t)=[x1(t),x2(t),…,xn(t)]T,t∈T为函数型协变量,t表示某一时间段,T为整个时间段;y=(y1,y2,…,yn)T为标量响应变量;β(t)表示斜率函数;ρ为空间相关系数;W为空间权重矩阵;ε为残差项,并假设ε服从多元正态分布N(0,σ2I),其中σ2为残差的方差,I为单位矩阵。
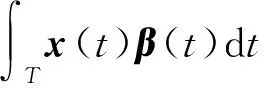
1.2.1 函数型主成分基展开
假设总体为x(t),记K(s,t)=Cov[x(s),x(t)]为x(t)的协方差函数,根据Mercer’s 引理有协方差函数的谱分解,可表示为[16]
(2)

第i个观测值xi(t)的Karhumen-Loéve展开式可表示为
(3)
在实际应用中,φj(t)是未知的,因此通过样本协方差函数的谱分解来估计特征函数φj(t),即考虑样本协方差阵,可表示为

(4)
(5)
式(5)中:aj=(a1j,a2j,…,anj)T。
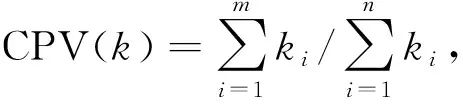
(6)
1.2.2 FSAR模型的极大似然估计
根据近似FSAR模型[式(6)],用极大似然方法估计未知参数,令A=(aij)n×m,b=(b1,b2,…,bm)T,从而式(6)可写为
y≈ρWy+Ab+ε
(7)
基于前面的假设ε服从多元正态分布N(0,σ2I),y的似然函数为
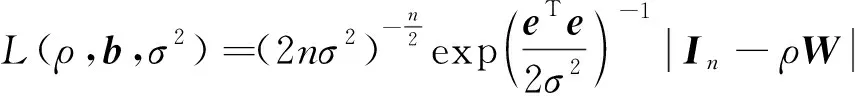

(8)
式(8)中:e=y-ρWy-Ab,先给定ρ,可得到b和σ2的极大似然估计分别为
(9)
(10)

(11)
通过最大化式(11),可求得ρ的估计量为
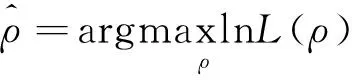
(12)

(13)
2 汾渭平原SO2与气温的函数型空间 自回归分析
分别对2019年汾渭平原地区11个城市的7项空气质量数据[PM2.5、PM10.0、SO2、NO2、O3和CO的监测数据及空气质量指数(AQI)],运用R、Geoda等软件进行空间自相关分析,采用rook矩阵为空间权重矩阵。首先对年均空气质量进行空间自相关分析,年均空气质量的空间相关性是否显著,由Moran’sI指数验证,结果如表1所示。
表1结果显示:这7项空气质量数据中SO2浓度和O3具有较强的空间自相关性,且SO2浓度的空间自相关性非常显著,P远小于0.05。选取7项空气质量数据中的SO2浓度数据与气温数据进行函数型空间自回归分析。由于所研究的是2019年每月SO2浓度与该月气温之间的关系,故对每月的SO2浓度进行Moran’sI检验,如表2所示,结果显示每个月这11个城市的SO2浓度都具有很强的空间自相关性,这说明运用FASR模型分析方法是合理有效的。

表1 2019年汾渭平原11个城市的年均空气 质量Moran’s I值Table 1 Moran’s I value of annual average air quality of 11 cities in Fenwei Plain in 2019
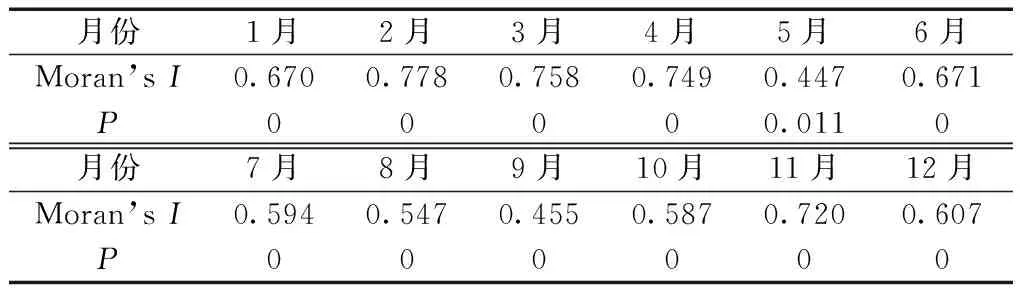
表2 2019年汾渭平原11个城市SO2月均Moran’s ITable 2 Monthly average of Moran’s I in SO2 in 11 cities in the Fenwei Plain in 2019
2.1 气温曲线的动态分析
选取汾渭平原11个城市2019年的逐时气温数据和逐月SO2浓度数据,观察发现收集到的逐时气温数据具有周期性,故采用傅里叶基样条函数拟合2019年每月的逐时气温曲线xi(t),i=1,2,…,11,并将其作为函数型空间自回归模型的协变量,平滑曲线如图2所示,为验证原始数据与平滑曲线之间的拟合效果,计算各月拟合曲线的均方根误差(root mean squared error,RMSE),结果如表3所示。

表3 各月份拟合曲线的均方根误差Table 3 RMSE of the fitted curve for each month
从图2可以看出,2019年汾渭平原11个城市的温度变化趋势大体相似,每日气温呈周期性变化。汾渭平原一年四季温差较大,冬冷夏热,最高温出现在8月份,最低温出现在1月份。1—7月温度持续上升,8月达到最大,之后温度又持续下降。通过导函数刻画了气温的动态变化特征,如一阶导函数(图3)及二阶导函数(图4)所示。

图2 2019年每月逐时气温变化曲线Fig.2 Hourly temperature change curve of each month in 2019
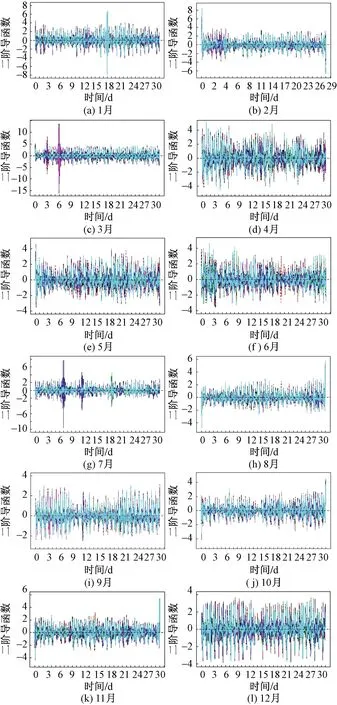
图4 11个城市每月温度曲线的二阶导函数Fig.4 The second derivative function of monthly temperature curve in 11 cities
图3为温度曲线的一阶导函数图,表示的是温度的上升或下降状态,一阶导函数大于零时温度上升,小于零时温度下降。图4为温度曲线的二阶导函数图,表示温度上升或下降速度的快慢。从图中可以发现,11个城市每日的温度上升和下降的变化相似,3、4、5月的一阶导函数图波动较大,这说明这3个月的每日温度变化较大,且当月的最低温与最高温相差30 ℃左右。
2.2 函数型空间自回归分析
利用前面所述的函数型空间自回归分析方法,基于R语言编写的程序实现汾渭平原11个城市的SO2浓度与气温曲线的函数型空间自回归实证分析。以2019年每月的逐时气温曲线xi(t),i=1,2,…,11为函数型空间自回归模型的协变量,月均SO2浓度yi为响应变量,建立函数型空间自回归(FSAR)模型为

(14)
式(14)中:yi′为第i′个城市的月均SO2浓度;wii′为城市i和i′之间的权重;εi为第i个等式对应的残差。
为了分析汾渭平原11个城市之间的SO2浓度存在空间自相关性,同时考虑普通的函数型线性模型(functional linear model,FLM)为
(15)
式(15)中:响应变量yi和函数型协变量xi(t)分别表示2019年第i个城市的月均SO2浓度和该月对应的逐时气温曲线;β(t)、γ(t)为斜率函数。
为了估计式(14)、式(15)中的斜率函数β(t)、γ(t),使用函数型主成分分析降维, 基于主成分基函数的FSAR模型和FLM分别表示为
(16)
(17)

首先利用函数型主成分分析方法对2019年汾渭平原11个城市12个月的气温变化曲线分别提取了前4个主成分,特征值及其累积方差贡献率如表4所示。
根据表4发现当取前4个主成分时累积方差贡献率均在94%以上,包含了数据足够多的信息。基于函数型主成分分析对气温函数完成降维,将无限维的FSAR模型转换为了空间自回归模型和函数型线性模型转换为了多元线性模型,可表示为
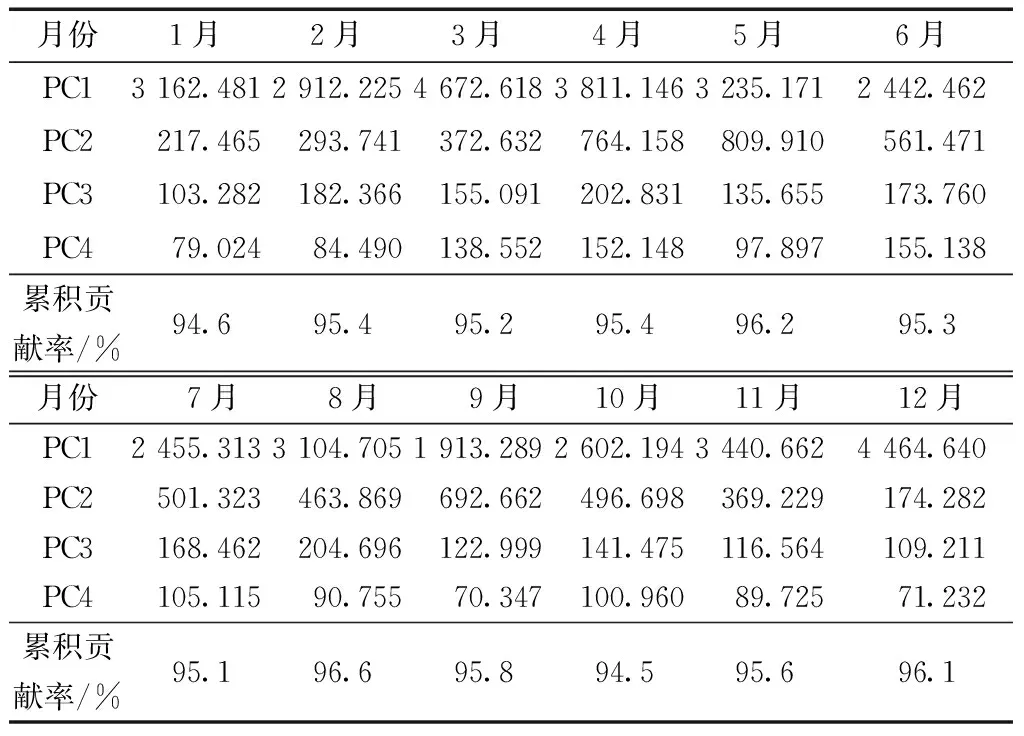
表4 函数型主成分分析特征值及其累积贡献率Table 4 Functional principal component analysis characteristic values and their cumulative contribution rate
(18)
(19)

采用1.2节介绍的估计方法进行函数型空间自回归分析,并对β(t)进行估计,斜率函数的估计结果如图5所示。

图5 每月FSRA模型的斜率函数β(t)Fig.5 Slope function β(t) of monthly FSRA model
观察图5可知,每月β(t)为负的区域均大于β(t)为正的区域,这说明从整体上看气温与SO2浓度呈负相关,并结合图3每月气温一阶导函数图像可以发现,气温上升时,对SO2浓度的负影响较小,气温下降时,对SO2浓度的负影响较大,2月的β(t)为负的面积在全年中是最小的,其次是1月、8月的β(t)为负的区域在全年中是最大的,其次是7月。从每天的温度变化趋势来看,气温每日呈周期性变化,其对SO2浓度的负影响也呈周期性变化,在每日气温上升的时间段内,对SO2浓度的负影响比较小,在温度下降的时间段内,对SO2浓度的负影响较大。
根据表5均方误差(mean absolute error,MSE)可知,FSAR模型拟合的响应变量MSE明显低于FLM的MSE,这说明FSAR的拟合效果更好,这两种方法的MSE平均相差7倍以上,12月份的差别最大。从图6可以看出,FSAR与FLM之间的差异,同时观察到FLM模型的MSE在全年呈现明显的季节性差异,在冬季MSE很大,夏季很小,很大一部分原因是由于汾渭平原冬季供暖[19]这一人为因素造成,而FSAR并没有很明显的这类变化规律,这说明FSAR模型降低了人为因素的误差影响。冬季FSAR模型效果明显,而FLM拟合的MSE 全年远大于20,这说明FSAR 模型能够很好地反映汾渭平原11 个城市的2019每月SO2浓度之间的空间自相关性,而FLM不能有效地解决这种相关性。可见,面对具有空间属性的数据时,函数型空间自回归模型拟合效果更好。

表5 FSAR模型与FLM模型的响应变量均方误差比较Table 5 Comparison of mean square error of response variables between FSAR model and FLM model

图6 每月FSAR模型与FLM模型SO2浓度均方 误差直方图Fig.6 Monthly mean square error histogram of SO2 concentration in FSAR model and FLM model
3 结论
借助函数型数据分析的思想并与空间自回归模型结合,针对汾渭平原特殊的地理位置和空气质量数据与气象数据的关系,运用函数型空间自回归模型分析该区域2019每月SO2浓度与当月气温曲线的关系。由于气温数据是每小时观测一次,数据观测频率高且密集,而SO2浓度数据为月均数据,具有显著的空间相关性,为了不丢失数据中包含的大量信息,将温度数据拟合成函数曲线,把它看成随机向量,此时选择函数型线性模型和函数型空间自回归模型来处理这组数据。通过函数型数据分析与空间自回归模型结合的方式对汾渭平原的SO2与气温进行函数型空间自回归分析,得到如下结论。
(1)从空间自相关分析中可以看出,汾渭平原地区各市的SO2浓度和气温除了受本市影响之外,还均受相邻城市SO2浓度的影响,甚至比本市的影响更大。
(2)在运用函数型数据分析方法对逐时气温数据进行拟合成气温曲线后,对气温曲线求一阶导数和二阶导数,一阶导数显示汾渭平原气温呈周期性上升和下降,个别城市出现气温急剧变化情况。
(3)通过FSAR模型中系数函数β(t)的图像可以看出,气温曲线与SO2浓度之间有显著的负相关性。对比函数型空间自回归模型和函数型线性模型,可以发现FSAR模型能够很好地反映汾渭平原11个城市的2019每月SO2浓度之间的空间自相关性,拟合效果更好。
(4)函数型空间自回归模型不仅能在宏观上分析全年气温的变化对SO2浓度,而且在微观上针对每小时的气温变化对SO2浓度的影响也清晰可见。并且通过对比FLM和FSAR的MSE,发现FSAR模型大大降低了人为因素所带来的误差。
气温曲线和SO2浓度是研究大气污染的两个重要指标。随着收集数据的方法越来越精细化,学者们不仅在意宏观上数据信息,更重视微观上的分析所带来更多更精确的信息,因此高频数据的处理方法变得至关重要,函数型数据分析方法也受到人们的普遍关注。将函数型数据与带有地理信息的数据结合,分析它们的空间分布特征和规律,函数型空间自回归将成为近代气候工作者关心的一个重要方向。

