基于预测变量图结构的高维逻辑回归模型*

黄文静， 邓 丹， 杜杰琳， 吴明月

(重庆医科大学 公共卫生与管理学院，重庆 400016)

0 引 言

随着信息和技术的快速发展，数据搜集能力越来越强，数据的规模和复杂程度都是前所未见的，特别是激增的变量维数给传统的统计学带来了巨大挑战。在高维情形下，变量个数p要大于样本量n，而且高维变量之间通常具有很强的相依性，此时，设计矩阵X不是满秩的，回归参数的估计往往也不是唯一的[1]。因此，如何对高维变量建模和参数估计是统计学关注的重点问题。正则化方法是处理高维数据常用的一种方法。Lasso[2]是人们熟知的正则化方法，但是当数据中存在某种结构(如组结构)时，Lasso不能很好地利用这种结构。因此，作为Lasso的推广，随后进一步提出Group Lasso[3]和Overlapping Group Lasso[4]等，这些方法在高维数据分析中均得到了广泛的应用，但是这些方法通常需要提前给出预测变量的组结构，然而在有些应用中很难得到这种结构。相比组结构，预测变量的图结构更容易获得。在生物学研究中，每个个体包含了成千上万的基因，这些基因有的单独作用，有的相互作用，而基因之间相互作用的大量信息可以用来构建预测变量的图结构，其中基因表示图中的节点，调控关系表示图中的边。即使在没有先验信息的条件下，仍然可以通过协差阵(精度矩阵)的稀疏估计[5-7]构造这些基因的图结构。Yu和Liu[8]在线性模型的框架下,提出一种利用预测变量图结构的方法，该方法具有一定的普遍性。目前，逻辑回归是处理分类数据的有效工具，正则化方法也被广泛应用于处理大p小n的逻辑回归问题[9-10]，本文将在文献[8]的基础上将图结构应用到逻辑回归模型中，为了评价这一方法的性能，将其与现有的许多方法进行比较，研究比较了不同图结构下的仿真实例，还将其应用到乳腺癌基因实例中，仿真实验结果和实际数据分析表明：该方法在估计、预测和模型的变量选择上均具有优越性。

1 基于预测变量图结构的逻辑回归模型

1.1 逻辑回归模型的改进

设(X,Y)为随机变量，其中X∈Rp，Y∈{0,1}。假设X服从均值为Op×1，协差阵为Σ的多元正态分布。给定X=x，Y的条件分布记为Pβ*(Y=1|x)=pβ*(x)。逻辑回归模型为

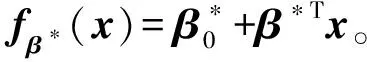
损失函数为

(

β

)=

(

β

;

x

,

Y

)= -

Yf

β

(

x

)+ log(1+exp(

f

β

(

x

)))

相应的风险函数和经验风险函数分别记为

P(β0,β)=E(β0,β;X,Y)

Pn(β0,β)=

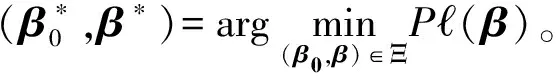
由文献[12]的定理2.1及文献[13]的条件3.1，有

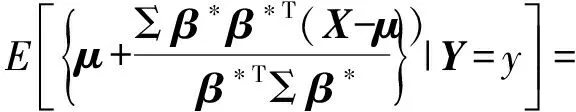
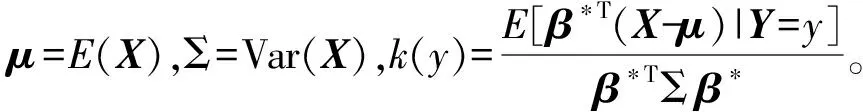
β*∝Σ-1(η(y)-μ)

(1)

令Σ-1=Ω=(ωij)i,j=1,2,…,p，其中Ω为精度矩阵，由式(1)可知，β*可表示为β*=Ωγ，γ=η(y)-μ。因此，文献[10]的方法可以推广到逻辑回归模型，于是有

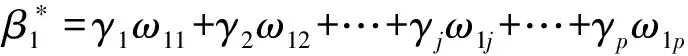
(2)

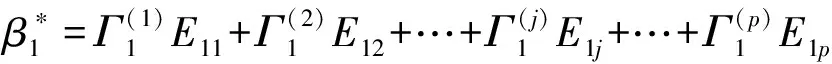
(3)

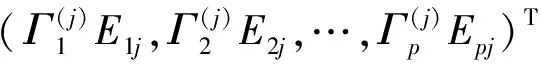
基于预测变量的图结构G确定领域N1,N2,…,Np(注意到j∈Nj,j∈Nj,j=1,…,p)。

求解如下优化问题：

(4)

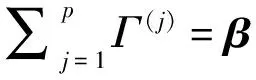
1.2 优化求解及权重参数的选取

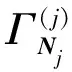
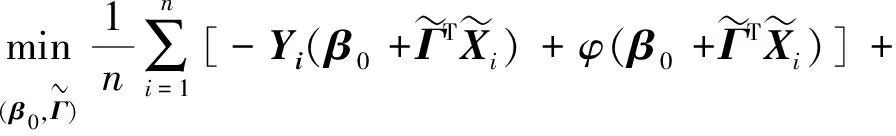
(5)

目前，有很多R包可以求解优化问题式(5)，如grpLasso[9]，grpreg[15]以及gglasso[16]。本文利用Zeng和Breheny[9]提供的R包求解优化问题式(5)，该方法能够直接求解重叠组结构的Group Lasso 问题。

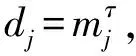
相比于目前流行的正则化方法(如Lasso，Group Lasso等)，本文的方法更具一般性。当预测变量的图结构没有边时，本文方法等价于Adaptive Lasso；当预测变量的图结构由若干个独立的完全图组成，本文方法等价于Group Lasso；当预测变量的图结构为完全图时，本文方法与岭回归有相同的非零解[11]。因此，本文的方法是一种更加一般的方法，Adaptive Lasso,Group Lasso和岭回归都可以看作是本文所提方法的特例。另外，本文的方法也可以用来处理Overlapping Group Lasso问题。

2 数值模拟

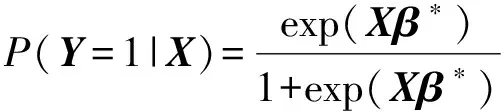
例1 (Ω分块对角)p=100，s*=15，真实的系数向量β*=(0.3,0.3,…,0.3,0,0,…,0)T，预测变量按如下方式生成：

Xj=Z1+0.4εj,Z1～N(0,1), 1≤j≤5Xj=Z2+0.4εj,Z2～N(0,1), 6≤j≤10Xj=Z3+0.4εj,Z3～N(0,1), 11≤j≤15Xj～N(0,1), 16≤j≤100

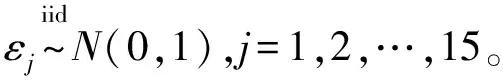
例2 (Ω带状)p=100，β*与例1相同，预测变量(X1,X2,…,Xp)T～N(0,Σ)，其中Σij=0.5|i-j|。此时，若|i-j|=1，有ωii=1.333，ωij=-0.677；若|i-j|>1，则ωij=0。

例3 (Ω稀疏)p=100，预测变量(X1,X2,…,Xp)T～N(0,Ω-1)，其中Ω-1=B+δI。B中非对角线元素以概率0.05取0.5，以概率0.95取0，对角线元素为0。选取δ使得Ω的条件数为p。令β*=Ωγ，其中γ=(γ1,γ2,…,γp)T，且γi=0.1,i=1,2,3,4，否则，γi=0。

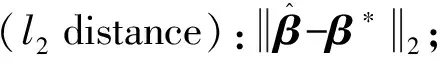
表1—表3给出了不同方法在不同的图结构中的表现，其中l2距离和预测误差衡量的是模型的估计和预测能力，RFPR和RFNR衡量是模型的变量选择能力。LG-O和LG表示本文所提方法分别利用真实图结构和估计图结构得到的结果。表1—表3中的结果表明：当图结构比较简单时，本文方法与其他方法相当(表1所示)；当图结构比较复杂时，本文方法无论从估计和预测方面还是从模型选择方面都明显优于其他方法，与具有Oracle性质的SCAD和MCP方法比较仍具有优越性(表2，表3所示)。

表4给出了不同方法RNMR和RZMR的表现。表4结果表明:即使图结构比较简单时，其他方法的RNMR和RZMR也很差。本文的方法在图结构较简单时明显优于其他方法，当图结构较复杂时，也要优于其他方法，这表明本文方法有效地利用了预测变量图结构的信息。

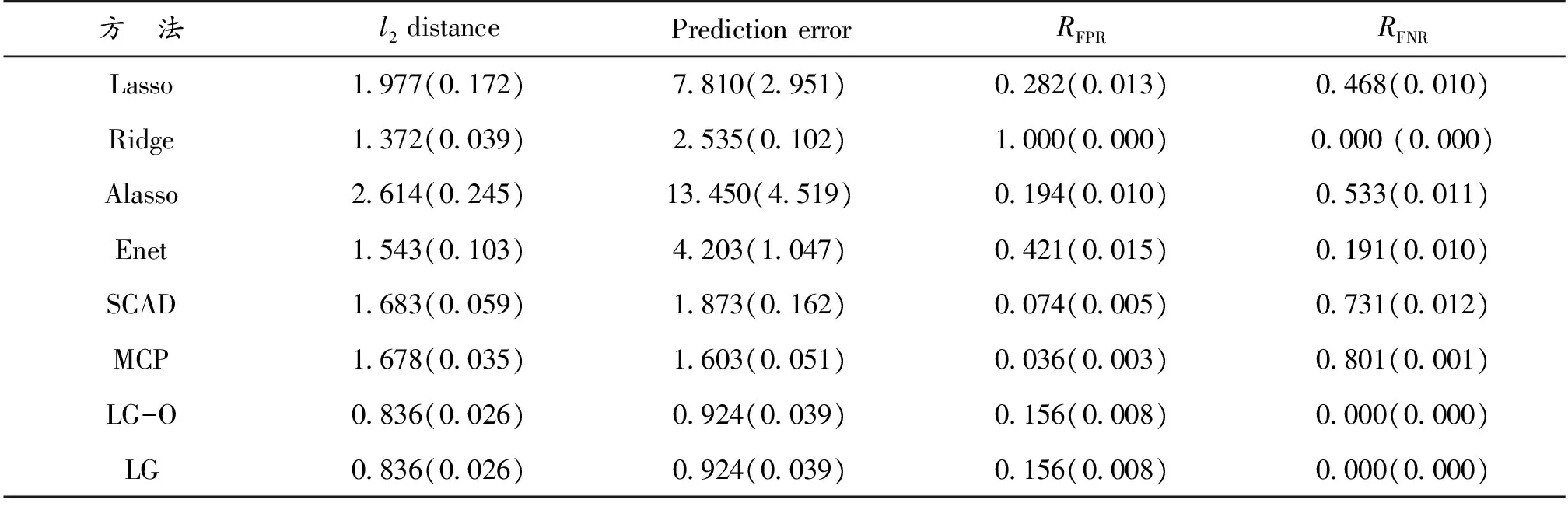
表1 例1中不同方法在模型估计、预测和模型选择能力的比较

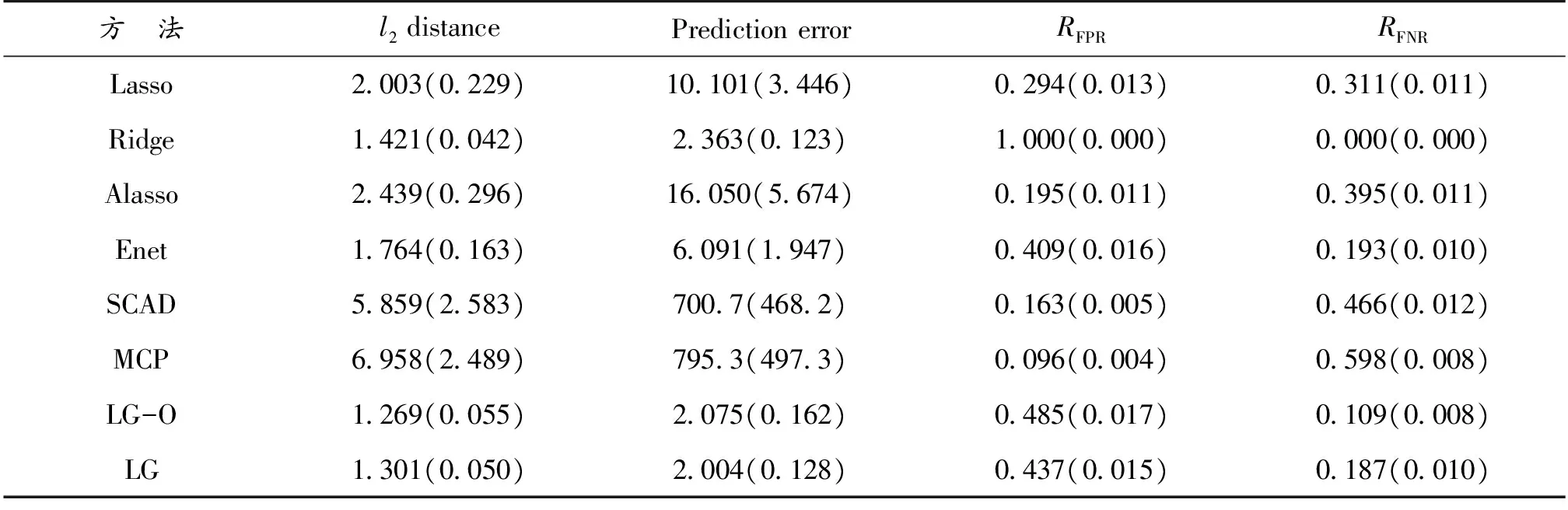
表2 例2中不同方法在模型估计、预测和模型选择能力的比较

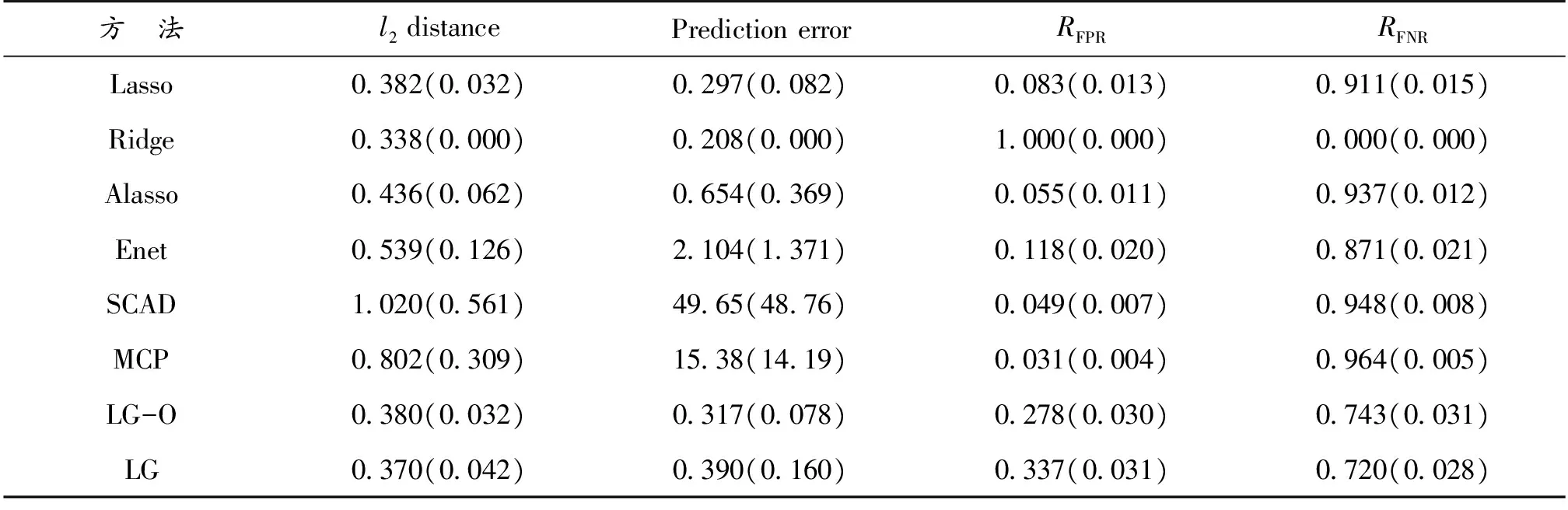
表3 例3中不同方法在模型估计、预测和模型选择能力的比较

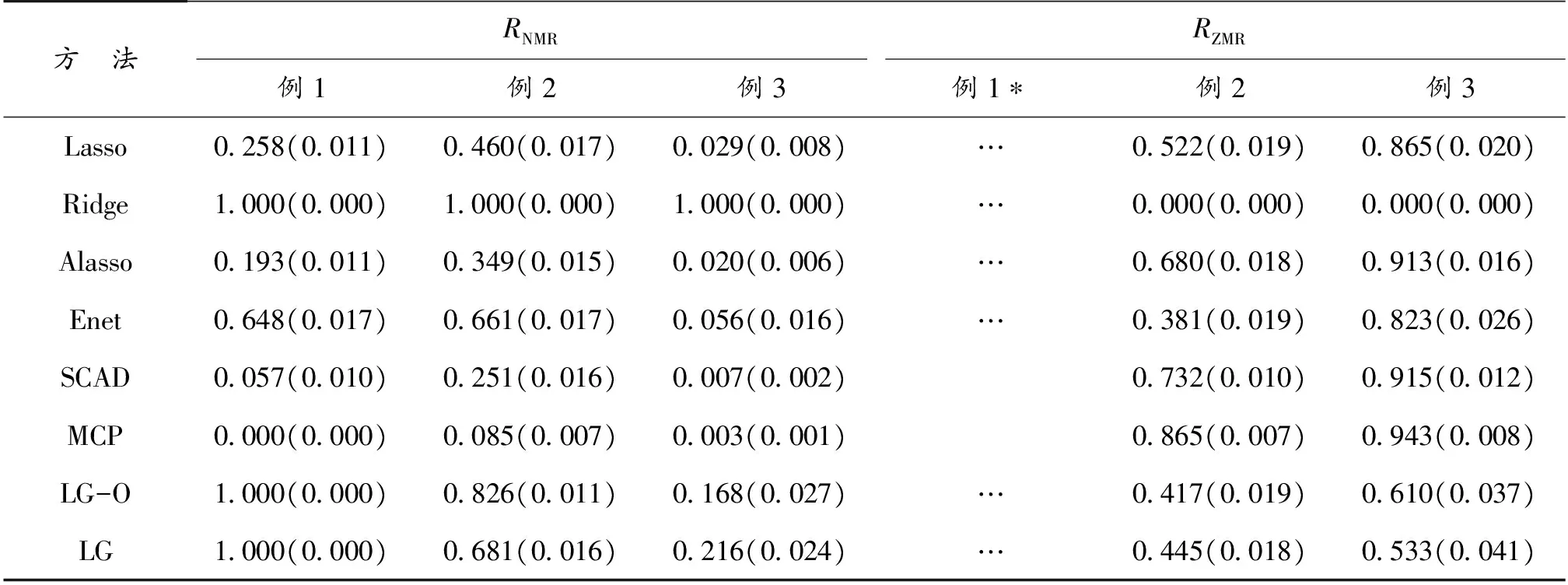
表4 不同模型的NMR和ZMR的比较

*注：…表示不可用值，没有用的预测变量之间没有相连的边。

以上模拟结果表明：即使图结构未知，本文方法仍然能够有效地利用预测变量图结构信息，从而提高模型在估计、预测以及变量选择等方面的表现。

3 实例分析与应用

本节将上述方法应用于公开的乳腺癌实际数据，包括133名受试者22 283个基因表达水平，其中34名为病理完全反应(pCR)受试者，99名为残留病(RD)受试者。该数据可以通过网址http://Bioinformatics. mdanderson.org/pubdata.html下载。考虑到迭代算法运行的速度以及计算机的限制，将主要比较本文的方法与Lasso方法、岭回归方法、Adaptive Lasso方法以及Elastic Net方法的效果。

为了估计精度矩阵，将数据集和测试集分别随机划分为大小为112和21的两部分，然后将整个过程重复100次。每次都采用分层抽样的方法从对应的组中选取5个pCR个体和16个RD个体作为测试集(大体相当于每组的1/6),其余的个体作为训练集。在每个训练集上，利用两样本t检验选取最显著的113个基因作为预测变量。注意到，训练集的样本量为n=112，比变量的维度p=113稍小，这一点可以用来检验p>n时各种方法的表现。利用训练集估计精度矩阵Ω，基于该精度矩阵利用Graphical Lasso估计预测变量的图结构G，其图结构如图1所示，图中包含113个节点，190条边。训练集用来拟合模型。利用测试集数据计算均方误差值(FMSE)来评估模型,利用10折交叉验证选取调节参数[7,17]。

实例分析结果如图2所示，图2给出了不同方法在对乳腺癌数据进行建模分析时的平均均方误差箱线图。结果可以看出本文的方法在MSE的表现上优于Lasso方法、Adaptive Lasso和Elastic Net方法，比岭回归的结果稍差。实际数据分析结果与数值模拟结果一致，说明该方法有效。

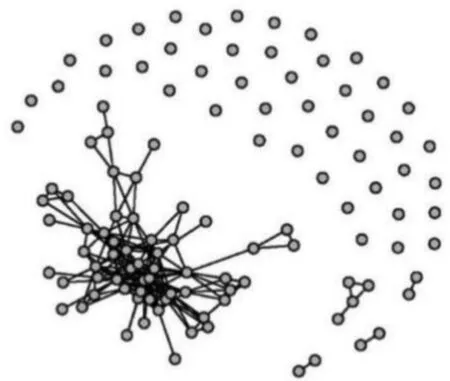
图1 乳腺癌数据的图结构

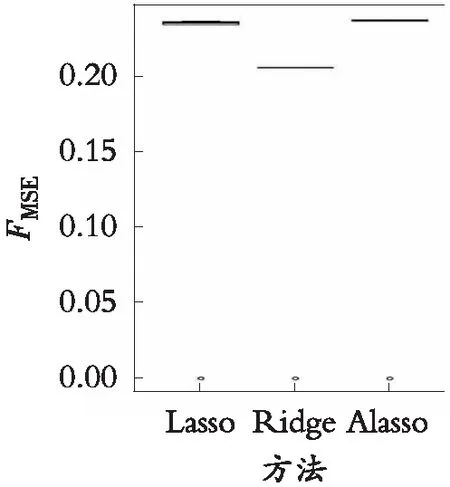
图2 乳腺癌数据集中不同方法的FMSE

4 结论与讨论

提出一种基于预测变量图结构的高维逻辑回归模型，该模型可以用来对高维图结构数据或者重叠组结构数据进行逻辑回归建模，即使预测变量的图结构未知，本研究的方法仍然能够利用这种结构提高模型在估计、预测以及变量选择等方面的表现。另外，目前流行的方法，如Lasso方法、Group Lasso和岭回归方法等都可以看作是本文模型的特例。数值模拟和实例分析应用表明：该模型在有限样本情形下是有效的，并且可广泛应用于高通量基因数据中存在图结构的疾病分类研究中。