霍乱传染病行波解的上下解计算*

秦 双 钰

(重庆工商大学 数学与统计学院，重庆 400067)

0 引 言

霍乱是一种典型的水源性传染病，具有多种传播途径，包括人与人之间的直接传播和人与被污染水源之间的非直接传播。据世界卫生组织统计，每年全世界约有300×104～500×104霍乱病例，有10×104～12×104人因此死亡。尤其是在许多发展中国家，近年来都有不同程度的霍乱爆发。

从20世纪开始到现在，研究学者发表了很多关于水源性传染病的文章，主要研究其传染方式、稳定性分析、控制策略等。Capasso和Paveri-Fontana[1]最早在1973年提出一个较为简单的霍乱模型；随后，Codeco[2]于2003年首次计算在水源环境中霍乱弧菌的浓度，建立改进的SIRB霍乱模型；Hartley等[3]考虑霍乱多途径传播的特点，将霍乱病菌分为高感染阶段和低感染阶段，结合两个新的环境元素构建一个高维霍乱传染病模型，能更精确地描述霍乱传染病的传播特点；Mukandavire等[4]再将Hartley的模型进行一些简化， 采用非线性发生率来描述人与被污染水源之间的传播；Liao和Yang[5]首次在霍乱模型中引入媒体效应，构造带媒体效应的多时滞霍乱模型，分析媒体效应和多种不同时滞对霍乱传播的影响；Wang等[6]研究了一个反应扩散霍乱模型，计算该模型的基本再生数、全局渐近稳定以及图灵不稳定性。更多的相关研究可参考文献[7-10]。

行波解是对传染病进行建模研究的一个关键因素，具有重要的研究意义，只要人们离开传染病源的速度大于行波解的速度， 就不易被传染，而行波解稳定与否可以直观反应传染病的传播形态会不会发生很大的变化。Tian和Yuan[11]研究一个带非局部扩散的SEIR模型， 计算最小波速和行波解；Zhang和Liu[12]分析一个SVIR传染病模型，同样计算最小波速和行波解；Wang和Wu[13]建立具有非局部时空延迟的扩散传染病模型， 利用Schauder不动点定理证明行波解的存在性；Chen[14]等研究格微分模型上的最小波速以及行波解的存在性和不存在性。更多的相关文献可参考文献[15-18]。

本文拟针对一类方程个数和参数较多的霍乱传染病模型进行行波解研究，构造一对明确的上下解函数来研究行波解的存在性。

1 建立霍乱模型

霍乱传染病是一种具有多种传播途径的复杂传染病，本文在文献[13-14]的基础上，建立如下带扩散项的偏微分方程组模型：

其中：S(x，t)，I(x，t)，R(x，t)分别表示易感者、感染者和移出者，在t时刻x处的密度；W(x，t)表示t时刻在水源x处的霍乱病菌浓度；Δ为拉普拉斯算子；参数βW，βI分别表示环境与人之间和人与人之间的传播率；Λ是自然的人类出生人数/死亡人数；μ是自然的人类出生率/死亡率；u>0是由疾病引起的死亡率；γ是恢复率；ξ是脱落率；δ是细菌死亡率；di(i=1，2，3，4)为正扩散率系数；模型中的所有参数均为正数。

注意到前3个方程中均不含R，即R具有独立性，故在后面的计算中只考虑前3个方程组。

基本再生数R0为

2 模型行波解的计算

令(S(x，t)，I(x，t)，W(x，t))=(S(θ)，I(θ)，W(θ))，其中θ=x+ct，常数c为波速，则行波方程变为

且系统满足边界条件如下：

易得系统在E0处的线性化系统为

令I=ηIeλθ，W=ηWeλθ，其中ηI，ηW为正常数，通过简单计算可得特征方程：

hI(λ，c)=d2λ2+βIS0-(μ+u+γ)-cλ

hW(λ，c)=d3λ2-δ-cλ

当R0>1，c>c*时，系统满足边界条件的非负非平凡解，首先可构造如下形式的上下解：

其中：M1，M2，ε1，ε2均为正参数，且将在后文对这些参数进行进一步讨论。任取ε>0，存在常数q1，q2满足：

hI(λ0+ε，c)q1+βIS0q2<0

hW(λ0+ε，c)q2+δq1<0

Λ-[(βWη3+βIη2)eλ0θ+μ]S0≤0

故引理1得证。

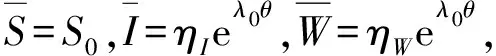
[hI(λ，c)ηI+βWS0ηW]eλ0θ≤0

βWS0(μ+γ-βIS0)+βIS0βWS0-(μ+γ)βWS0≤

故引理2得证。

ξβWS0-δ(μ+γ-βIS0)=0

故引理3得证。

βWS0(1-M1eε1θ)η3e(λ0-ε1)θ-

βIS0(1-M1eε1θ)η2e(λ0-ε1)θ]≥

(βWη3+βIη2)e(λ0-ε1)θ]

即可得证。

hI(λ0，c)ηIeλ0θ-hI(λ0+ε2，c)M2q1e(λ0+ε2)θ=

eλ0θ[hI(λ0，c)ηI-hI(λ0+ε2，c)M2q1eε2θ]

由前面hI(λ0+ε2，c)<0，可知-hI(λ0+ε2，c)eε2θ必为θ的单调递增数，必有

又由于

[d2(λ0+ε2)2-c(λ0+ε2)-

(μ+u+γ)+βIS0]M2q1e(λ0+ε2)θ-

βIS0M1eε1θeλ0θ(ηI-M2q1eε2θ)=

hI(λ0，c)ηIeλ0θ-hI(λ0+ε2，c)M2q1e(λ0+ε2)θ-

βIS0M1ηIe(λ0+ε1)θ+βIS0M1eε1θM2q1e(λ0+ε2)θ=

hI(λ0，c)ηIeλ0θ-βIS0M1ηIe(λ0+ε1)θ-

[hI(λ0+ε2，c)-βIS0M1eε1θ]M2q1e(λ0+ε2)θ

此时，只要

不等式即可成立。故此引理5得证。

[d3(λ0+ε2)2-c(λ0+ε2)-δ]M2q2e(λ0+ε2)θ≥

hW(λ0，c)ηWeλ0θ-hW(λ0+ε2，c)M2q2e(λ0+ε2)θ≥0

[d3(λ0+ε2)2q2-c(λ0+ε2)q2-δq2+ξq1]M2e(λ0+ε2)θ≥

[(hW(λ0，c)ηW+ξηI)]eλ0θ-

[hW(λ0+ε2，c)q2+ξq1]M2e(λ0+ε2)θ≥

-[hW(λ0+ε2，c)q2+ξq1]M2e(λ0+ε2)θ≥0

3 结束语

针对一类具有多种传播途径的霍乱传染病，建立带扩散项的偏微分方程组模型进行研究。为了计算该模型的上下解，克服了模型维度较高以及参数较多的困难，找出了明确的上界和下界函数，并证明了上下界函数满足边界条件，这也是本文有别于其他文献的地方。但是还没有针对基本再生数小于1时，对行波解的不存在性进行讨论，这就是未来的重点工作之一。