机场出租车司机的最优决策模型*

陈修素， 陈 睿

(1.重庆工商大学 数学与统计学院，重庆 400067; 2.重庆财经学院，重庆 401320)

0 引 言

随着科技的发展、社会的进步和生活水平的不断提高，飞机已成为人们长途旅行的重要交通工具，乘客下飞机后要去市区或周边目的地，出租车以其灵活便捷的特点，成为多数人首选的交通工具。出租车司机将市内乘客送到机场之后，将会面临两种选择:一是前往“到达区”排队等待载客返回市区，花费一定时间等待下飞机乘坐出租车的乘客，将他们运载回市内，得到相应的收益；二是立刻放空返回市区接单拉客，得到收益，损失潜在的机场载客收益并付出空载费用。出租车司机的两种不同决策选择导致所获得的净收益不同。出租车司机这两种不同决策净收益的影响因素有许多，包括在一定时间段内到达机场的飞机航班数、飞机机型和乘坐率、机场乘坐出租车的乘客比率、此时段在“蓄车池”排队等待的出租车数量、此时市区出租车服务密度等。韩中庚[1-2]给出了载客出租车机场等待的时间成本和空载返回市区的出租车潜在总损失，比较空载返回成本和等待时间成本的大小关系并由此构建机场出租车司机的决策模型，但其忽略了机场出租车所载乘客多为长途，其在单位时间的收益远高于市区载客的收益;俞雪永等[3]综合考虑了一定时间段内排队等待的出租车数量、到达机场的乘客数量、乘坐出租车的乘客数量、此时间段内市区出租车服务密度、天气因素、节假日因素、司机的心理因素和驾驶状态给司机带来的决策影响等众多因素，并以这些因素为变量，构造了出租车决策模型，给出了出租车司机做出各种不同决策的阈值和相应的决策准则，从其实例分析的选择结果看出在时段6—10这5个时段(持续5 h)机场出租车都选择直接放空返回市区拉客，这与现实差异太大，主要原因是影响决策的部分次要因素——定量化权重的确定比较主观，且其综合作用被放大；王欣颖等[4]通过对天气状况、气温、风力3种天气因素进行定性和定量分析，给出天气最终得分，讨论此得分对乘坐出租车乘客的影响，进而建立了出租车司机的决策模型，在这些次要因素的定量分析中依然未能摆脱主观的因素。因此忽略次要影响因素及非主观的定量方法，将既包含载客前的等待时间又包含载客送达目的地的运送时间在内的一个完整周期内出租车司机的两种决策对应的单位时间所获净收益进行比较，由此构建出的机场出租车司机的决策模型就更显客观合理。

1 问题描述

当出租车司机已送客到达机场，如果已知某一时间段内到达机场的航班数量和机型、飞机乘坐率(可以依据历史数据进行经验估计)以及乘客数量、当前已在“蓄车池”排队等待的出租车数量、该时间段市区出租车服务密度等信息条件下，分析影响出租车司机决策的主要因素，并进行定量估计，根据机场乘客人数和等候的出租车数量及相应的时间点机场大巴及地铁(或轻轨)的运营密度变化等不同情况，综合考虑出租车司机不同选择的有关收益和费用，根据相同时间内单位时间的平均净收益构建出租车司机选择的决策模型，并给出出租车司机的最佳选择策略。

2 模型的建立

2.1 基本假设

假设机场乘客等候出租车和出租车载客点只有一个；假设在机场排队等待载客的司机，一定能接到乘客并送到市区；假设司机匀速行驶，单位时间内消耗费用相同；假设地铁(或轻轨)及机场大巴车可以分流部分前往市区的机场乘客；司机到达机场的时刻离换班有充足的时间，即司机的决策不受交接班因素的影响；假设每天出租车到达机场的时间间隔服从Poisson分布；每个泊位的上客能力相同。

2.2 问题分析

2.2.1 确定t时段乘坐出租车的候车人数

给出t时刻起单位时间内的候车人数H(t)的如下估计：

根据每个时间段到达机场的航班数、飞机机型以及乘坐率(用历史数据估计)，统计出各个时间段到达乘客的数量。设t时段飞机载客到达机场的总乘客数为Z(t)，根据当时机场大巴、地铁以及部分自驾车接走乘客等分流情况，估计获得选择乘坐出租车的乘客比例为B(t)，设机场乘客从下飞机到达出租车候车区的平均时间为νh,Y(t)是t时刻在候车还未上出租车的余下的候车乘客数，则t时刻起单位时间内的候车总人数H(t)可估计为

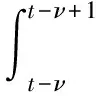
2.2.2 确定选择机场等待载客的出租车排队等待时间

如果每辆出租车从蓄车池到达乘车区需要的时间为t1；每组乘客上车需要时间[5]为t2：每辆车上完客后启动、离开乘车区需要时间t3。

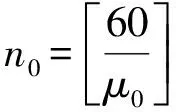
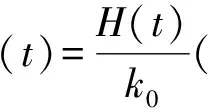
研究组治疗有效率为91.18%，对照组治疗有效率为79.41%，研究组在治疗有效率的比较上明显优于对照组（P＜0.05）。 见表 1。

此时每辆车的服务时间为μ(t)=μ0+τ(t)。则利用函数的平均值的公式[6]，可得每辆车的平均服务时间为

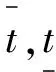
机场出租车司机排队等候乘客的系统可以视为多服务台的排队系统M/M/c/∞，假设在机场选择等候载客的出租车以简单流到达，参数为λ，服务台数为每次放行进入上客区域的出租车的最多台数，记为c，服务时间近似服从参数为μ的负指数分布，则利用排队论知识[7-8]，可得出租车的平均等待时间为

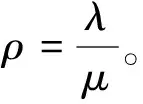
2.2.3 在机场等候载客的出租车司机载客的收益函数

假设出租车从机场搭载乘客xkm，出租车的起步价格为a0元，出租车的公里价为b0元/km，出租车油耗费c0元/km。由于一般城市规定单程载客行驶超过15 km部分，基本单价加收50%的费用，从而可得从机场搭载乘客xkm的出租车司机的净收益函数为R：

R=a0+b0min{12,max{x-3,0}}+ 1.5b0max{x-15,0}-c0x

由于搭乘出租车的乘客到达目的地的路程公里数x具有随机性，可根据在机场搭乘出租车的乘客到达目的地的公里数的历史记录数据，获得不同公里数的频率(比率)，进而获得乘客搭乘出租车的公里数x的概率密度函数f(x)的估计，则由概率论知识[9]，可得出租车司机的期望净收益如下：

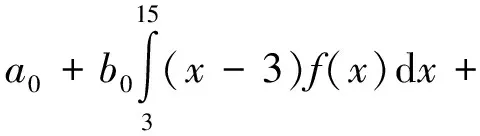
设出租车司机的载客的平均时速为v0km/h，则出租车司机的载客的平均时间为

则该出租车司机选择载客时，其单位时间所获得的平均净收益为

其中，T0是选择机场载客的出租车司机在机场的停留时间。

2.2.4 在机场直接返空的出租车司机的收益和费用函数

从出租车司机在机场选择等候载客开始到其搭载乘客到达目的地终止的这段时间(T0+t0) h里，对选择空载返回主城的出租车司机，设其空载返回主城市区所需时间为t1h，然后在余下的(T0+t0-t1) h内，估计出租车司机市区载客运营的平均收益为(T0+t0-t1)R1元(其中R1为司机在市区运营的平均每小时的净收益，可由历史数据进行经验估计)，则可得空载返回主城的出租车司机在相同的时间区间里，其单位时间的净收益为

3 机场出租车司机有关的主要模型

3.1 机场出租车司机的最优决策模型

到达机场的出租车司机面临的决策问题是从出租车司机在机场选择等候载客起到其搭载乘客到达目的地止的这段相同的时间(T0+t0) h里，哪一种选择对应的单位时间所获得的净收益最大，其对应的最优决策模型为

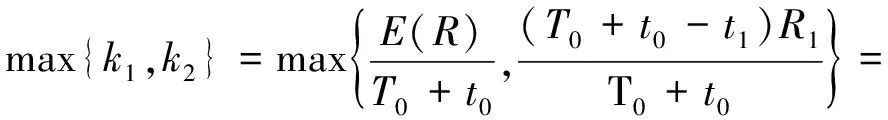
即如果k1k2，其最大值为k1，出租车司机选择机场等候载客更有利；如果k1=k2，出租车司机两种选择差别不大。

3.2 机场短途载客且再次返回机场载客的出租车排队的“优先权”模型

为了实现出租车司机收益的均衡化，对机场短途载客且再次返回机场载客的出租车，由于其单位时间所获得的收益明显小于一般机场搭载相对长途乘客的收益，为公平起见，需要给予其优先排队的权限，以便使得这类司机累积单位时间的平均净收益与其他司机保持均衡。为此，设某出租车司机在机场载一短途乘客xkm，其所获收益未达到机场出租车载客平均收益E(R)的75%(或某一个其他的比例)，对这部分短途载客且再次返回机场载客的出租车给予排队的 “优先权”。其建模思路如下：

设该出租车司机已在机场搭载短途乘客xkm，其所获净收益为

R=a0+b0min{12,max{x-3,0}}+ 1.5b0max{x-15,0}-c0x

元，且R≤75%E(R),该司机再次返回机场到达区的“蓄车池”，此时前面已有N辆出租车排队等候，则机场管理员将该出租车安排在“蓄车池”的第l辆位置排队等待。其上次载客净收益越小，安排其排队越靠前，给其优先权越大，按此规则可得确定l的如下方法：

该模型更能有效指导机场出租车的候车管理，操作上更便捷高效。而王欣颖等[4]仅给出了短途载客再次返回机场载客的出租车在快速通道应优先缩短的时间t,这不便于管理员具体确定究竟在何时放行出租车进入泊位上客。

在没有优先权的情况下，短程出租车司机要想和长途出租车司机获得相同的收益，需要比长途出租车司机付出更多的时间。故这里的优先权是可以理解为给予短途出租车司机返回时排队等待位置上的优先分配权，即减少短途出租车司机的等待时间。这里假设排队位置优先权给予的对象只针对再次返回机场“蓄车池”处排队载客，且已载客xkm获得的净收益低于司机的平均净收益75%(也可以选取其他某个具体的比例数)的司机。本模型如能运用智能匹配管理系统[10]，将能极大地提高机场的出租车管理效率。

4 结 论

定量分析了一定时间段内机场乘坐出租车的候车乘客数量、选择机场等待载客的出租车排队等待时间，给出了在机场等候载客的出租车载客的收益函数，以及在机场直接返空回市区的出租车的收益和费用函数，建立了既包含机场出租车载客前的等待时间又包含载客送达目的地的运送时间在内的一个完整周期内机场出租车司机两种不同决策对应的单位时间所获净收益的表达式，构建了机场出租车司机的最优决策模型和机场短途载客且再次返回机场载客的出租车排队的“优先权”模型。上述建模过程忽略次要因素的影响，避免了非主观的定量方法的运用，更能客观有效指导出租车司机的决策和指导机场出租车运营管理，提高机场出租车管理效率。