城市交通环境治理问题的演化博弈分析*

刘俊怡， 杨 辉， 杨光惠

(贵州大学 数学与统计学院，贵阳 550025)

0 引 言

近年来，我国城市交通快速发展，与此同时也存在很多问题。由于缺少健全的法律法规，并且管理环境复杂，运管、黑车、出行居民之间为了各自的利益，会产生互相冲突的现象[1]。对社会大环境下的交通有不良的影响，同时也不利于我国经济的发展。

随着人们生活水平的提高，城市居民基本形成以自己兴趣爱好、经济能力为参考的出行方式。由于某些城市的地理和交通情况的特殊性以及待业人群过多的社会现象，违规运营的黑电动车、黑摩托车、黑汽车市场猖獗，影响城市的形象、交通，大大增加交通事故的产生，扰乱交通行业市场。但部分城市居民的选择，和运管部门的不查处行为也助长了他们的非法运营。

近年来对于非法运营黑车的博弈问题，有不少学者进行了分析并提出对策[2]。如梁辉、田晟等[3-4]建立了黑车与相关管理部门的两策略演化博弈系统，并对遏制黑车市场给出了相关建议及对策，但未从出行居民的角度出发，仅考虑了两个博弈群体的系统；张芸珠等[5]也是将博弈系统建立在政府部门、出租车两个博弈方上，分析了政府约束出租车的最优策略，同样未考虑到多群体下的交通环境；张亚平、杨青等[6-7]分析交通环境中各主体之间利益关系，包括出行公众、驾驶人、出租车司机、政府几个利益主体，提出行业改革方案，构建出租车行业的良性发展机制，但是只是分析了各个主体之间的利益关系，并没有具体的用收益矩阵、复制动力学分析整个系统达到的平衡点以及演化稳定策略。

鉴于以上背景，根据群体博弈、演化博弈的相关基本理论[8-12]，对运管、黑车、出行居民这3个群体进行演化分析，得到在交通环境治理中这3个博弈群体决策行为的演化路径及最后趋近的演化稳定策略，并为城市交通环境治理提出相关政策性建议及措施。

1 城市交通环境治理的三方演化博弈模型构建

1.1 博弈主体分析及基本假设

演化博弈的参与主体包括：运管、黑车和出行居民，3个主体分别代表3个群体，每个群体内部个体的策略空间相同。运管的策略空间为{查处，不查处}；黑车的策略空间为{不出车，出车}；出行居民策略空间为{不坐黑车，坐黑车}。

1.2 模型基本假设

基于上述基本假设以及现实情况，作出进一步假设。

假设1 对于城市运管而言，若运管采取“查处”策略，通过惩罚黑车出车行为等措施，引导黑车行业市场逐渐变小，形成优良的城市环境，查处有效获得的社会收益g。同时，对黑车的出车行为实施监管(日常监管、专项监管、抽查监管等)产生的监管成本b。不坐黑车的居民对合理的交通运管查处形成好的口碑h，但对运管不查处会产生失望心理n。有效的查处导致城市中黑车数量变少，习惯于坐黑车的市民对运管部门产生抱怨i。

假设2 对于黑车群体而言，出车的收益为a。出车被运管查处产生罚款为c。出车导致城市交通环境负效应为m，从而增加政府、运管的治理成本f。

假设3 对于出行的居民群体而言，坐黑车给生活出行带来便利d，但坐黑车被运管部门查处会被口头警告产生不好的个人影响e。

假设4 假设运管群体中选择查处策略的比例为x，选择不查处策略的比例为(1-x)；黑车群体中，选择不出车策略的比例为y，选择出车策略的比例为(1-y)：出行居民群体中，选择不坐黑车策略的比例为z，选择坐黑车策略的比例为(1-z)。

通过以上模型的基本假设，可以得到运管、黑车和出行居民的博弈收益矩阵(表 1)。

表1 运管、黑车与出行居民的演化博弈收益矩阵

2 三方演化博弈均衡分析

2.1 三方博弈的复制动态方程[11]

Ua=hyz+(-i)·y(1-z)+(h+g)(1-y)z+g(1-y)(1-z)=iyz+(-i-g)y+hz+gUb=byz+b·y(1-z)+(b-f-n)(1-y)z+

(b-f)(1-y)(1-z)=nyz+fy-nz+b-f

运管的平均期望收益为

运管选择查处策略的复制动态方程为

(1)

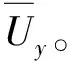
Uc=0·xz+0·x(1-z)+0·(1-x)z+ 0·(1-x)(1-z)=0Ud=(-c)xz+(a-c)x(1-z)+ 0(1-x)z+a(1-x)=

(-c)x-az+a

黑车的平均期望收益为

黑车选择不出车策略的复制动态方程为

(2)

Ue=0·xy+(-m)x(1-y)+ 0·(1-x)y+(-m)(1-x)(1-y)=my-mUf=0·xy+(-m-e+d)x(1-y)+ 0·(1-x)y+(-m+d)(1-x)(1-y)=exy-ex+(m-d)y-m+d

出行居民的平均期望收益为

出行居民选择不坐黑车策略的复制动态方程为

(3)

2.2 演化过程的均衡点

由式(1)—式(3)3个复制动态方程可得到三维动力系统式(4)：

(4)

令T1=i-n，T2=-i-g-f，T3=h+n，T4=g-b+f。则上述三维动力系统简化为

(5)

结论1 三维动力系统式(5)有23个3种群均采纳纯策略的平衡点：

A1=[0,0,0],A2=[0,0,1],A3=[0,1,0],A4=[0,1,1],A5=[1,0,0],A6=[1,0,1],A7=[1,1,0],A8=[1,1,1]

结论2 三维动力系统式(5)可能有3个单种群采纳纯策略的平衡点：

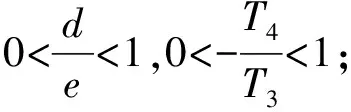
结论3 三维动力系统式(5)可能有3个2种群采纳纯策略的平衡点：

结论4 三维动力系统式(5)可能有1个混合策略平衡点：A15=[x*,y*,z*]，x*,y*,z*∈(0,1)。解方程组：

(6)

得A15=[x*,y*,z*]：

2.3 稳定性分析

用李雅普诺夫(第一法)来判断系统式(5)的15个平衡点A1～A15的稳定性：

(1)xe渐近稳定

⟺雅可比矩阵的所有特征值Re(λk)<0；

(2)xe李雅普诺夫稳定

⟺雅可比矩阵的所有特征值Re(λk)≤0，且

Re(λk)=0的特征值无重根；

(3)xe不稳定

⟺雅可比矩阵有一个特征值Re(λk)>0，或者Re(λk)=0的特征值有重根。

计算系统(5)的雅可比矩阵得到式(7)：

(7)

李雅普诺夫第一法规定判断系统平衡点的渐进稳定性是通过其对应的雅可比矩阵的特征值，因此需通过式(7)计算系统式(4)每个平衡点的所对应的雅可比矩阵的特征值(表2)，而后得到平衡点稳定性条件(表3)。其中：

表2 系统式(4)的平衡点及其特征值

表3 系统式(4)的平衡点稳定性条件

3 仿真分析

为了验证三方博弈的演化路径以及最终的稳定状态即演化稳定策略，将上述3个演化稳定性条件中的变量具体为数值，利用MATLAB软件代入数值验证A1、A5、A8这3个平衡点是否为演化稳定策略。具体参数值设定见表4。

(1) 需满足平衡点稳定性条件：g-b+f<0。取值b=5，g=3，f=1，使g-b+f=-1<0，其他数据见表4数组1。将数组1数据输入到MATLAB，输出见图1。可以看出系统最终演化稳定于A1=[0,0,0]，该点为演化稳定策略。

(2) 需满足平衡点稳定性条件：-g+b-f<0，c-a<0，e-d<0。取值a=6，b=5，c=4，d=3，e=1，g=4，f=2，使-g+b-f=-1<0，c-a=-2<0，e-d=-2<0，其他数据见表4数组2。将数组2数据输入到MATLAB系统，输出见图2。可以看出系统最终演化稳定于A5=[1,0,0]，该点为演化稳定策略。

(3) 需满足平衡点稳定性条件：-h+b<0。取值b=5，h=6，使-h+b=-1<0，其他数据见表4数组3。将数组3数据输入到MATLAB系统，输出见图3。从图中可以看出系统最终演化稳定于A8=[1,1,1]，该点为演化稳定策略。

表4 参数取值

图1 数组1路径

图2 数组2路径

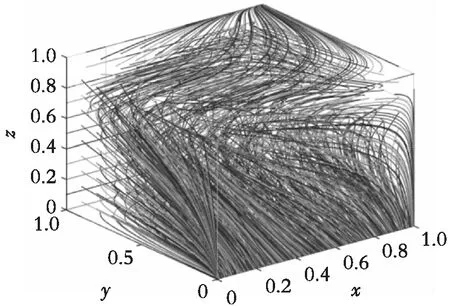
图3 数组3路径

4 演化结果的情景分析

以上对运管、黑车、出行的居民三方博弈的群体演化模型以及平衡点的渐进稳定性进行了分析，得到了演化稳定策略，并且用MATLAB成功地模拟了演化路径，验证了其演化稳定性，得到在城市交通治理中运管、黑车、出行的居民在符合不同的稳定性条件下，会各自趋于最终的演化稳定策略。具体将几种情景进行模拟：

情景1 博弈三方都对城市交通情况治理均不贡献自己的力量，即A1=[0,0,0]，这时必须满足条件g-b+f<0。运管查处成本大于查处有效的社会收益与再治理成本之和，所以运管部门的行为选择最终趋向于不查处，黑车群体的行为最终趋向于出车，同时出行的居民也最终趋向于坐黑车，这样城市交通的管理进入恶性循环阶段。因此有关政府部门要合理控制有效查处的社会收益，增加g的值，使得条件g-b+f<0不成立，那么系统的演化路径不会趋向于A1=[0,0,0]这个演化稳定点，城市交通不会进入恶性循环，减小城市交通治理的负面影响。

情景2 运管对城市交通情况予以治理，进行查处，但黑车、出行的居民不参与，即A5=[1,0,0]，这时需满足条件-g+b-f<0，c-a<0，e-d<0。运管查处成本小于查处有效的社会收益与再治理成本之和，此时在情景1的基础上，合理提升了有效查处的社会收益，运管的行为决策得到了改变，积极参与到城市交通环境治理中。但是黑车出车的收益大于被运管查处的罚款，黑车会趋向于出车，居民选择坐黑车时受到运管的警告及惩罚小于坐黑车给生活带来的便利，那么居民最终会趋向于坐黑车。这样城市交通环境仍旧混乱，违规运营黑车市场仍旧猖獗，未起到改善城市交通环境的目的，因此要合理增加被运管查处时对黑车司机罚款和车载居民的警告及惩罚。这样条件的后两个条件不成立，那么系统的演化路径不会趋向于A5=[1,0,0]这个演化稳定点。

情景3 博弈三方均投身于城市交通情况治理，即A8=[1,1,1]。这时必须满足条件-h+b<0，-c<0。城市居民或由于罚款严重不支持社会上出黑车行为，运管查处成本小于居民对合理的交通查处形成的社会口碑(社会收益)，同时运管查处黑车时必将做出罚款，且罚款金额大于其出车的收益。运管的行为最终趋向于查处，黑车司机会趋向于不出车，居民选择不乘坐黑车。城市交通环境治理问题的演化路径最终演化稳定于A8=[1,1,1]，治理进入良性循环，城市交通环境治理问题得以解决。

5 结束语

利用演化博弈复制动力学相关内容构建了运管、黑车、出行的居民三方为博弈主体的城市交通环境治理的演化博弈模型，并对系统的演化稳定策略进行了分析和模拟仿真。结果表明：某个单群体的平衡点稳定性除了由自身影响外，还受其他两个群体的影响；通过最后得到的演化稳定状态，可以得到，运管部门的查处对于交通环境治理起了重要的主导作用，但需要民众的口碑和有效的社会治理成果或社会收益做支撑。揭示了交通环境治理除了需要运管部门的积极查处，对黑车的违法运营行为以及坐黑车的居民缺乏惩罚的机制也是关键的一部分。在运管部门的查处下，仍然有黑车出车以及市民选择做黑车，因此应该合理地增加对黑车的罚款以及增加对市民的警告或处罚。