复波场的实部和虚部对同时源波形反演的影响

杨育臣，方金伟，王宁，李松龄

1 Geology and Geophysics Program，Missouri University of Science and Technology，Rolla，MO 65409，USA 2 深部岩土力学与地下工程国家重点实验室，中国矿业大学力学与土木工程学院，徐州 221116 3 东北石油大学地球科学学院，大庆 163318

0 引言

近年来，发展了宽频带、宽方位、高密度的地震数据采集技术，通过地震成像技术实现地下参数的高信噪比、高分辨率和高保真度的建模.其中，具有最高成像精度的反演成像以全波形反演(FWI)为代表，实现构造信息和岩性油气藏的高精度参数建模.全波形反演通过建立观测和合成数据的某种距离度量的目标泛函，利用优化理论计算出参数下降方向和更新步长，不断修改模型直至合成数据接近观测数据，从而获得准确的模型参数.全波形反演能够充分利用地震数据中的振幅和相位信息，获得高分辨率高精度的速度模型.

计算效率低下是制约全波形反演进行大规模计算以及实际资料处理的主要因素，因此提升全波形反演的效率就显得十分重要(邢贞贞等，2019).除了使用高性能计算平台加速之外(Yang et al.，2015；Gokhberg and Fichtner，2016；张猛等，2014；桂生等，2017)，通常使用算法类的效率优化方案来加速反演.基于算法类的加速方法通常使用震源编码策略提升全波形反演效.震源编码的思想是通过某种震源组合方式将很多单炮形成一个超级震源(编码炮)，实现几十炮甚至上百炮的同时模拟，从而减少全波形反演中波场模拟的次数，极大地减少全波形反演的计算量.然而，相比于传统的同时源模拟(震源编码)方法，比如随机源编码(Krebs et al.，2009)、随机时移(Dai and Schuster，2009)、平面波编码(Zhang et al.，2003；Vigh and Starr，2008)等算法，一种基于频率选择的同时源方法不仅能够保证计算效率，而且可以获得不受编码串扰噪声影响的反演结果.Huang和Schuster(2012)第一次在频率域全波形反演处理海洋观测系统数据时使用了该方法.而时间-频率域(混合域)的同时源反演方法最早由Dai等(2013)提出并用来加速最小二乘逆时偏移成像.在混合域同时源模拟方法中，将一系列不同频率的单频源组合起来形成了一个编码源，并在时间域完成波场的模拟.编码炮的梯度计算则是在频率域完成的，通过计算每一个单频子波对应的梯度然后叠加形成编码炮对应的梯度.这种方法的关键技术是如何准确地解耦混叠波场.Dai等(2013)采用离散傅里叶变换的方法实现了波场解耦，Huang和Schuster(2018)也是借鉴于这种滤波方法，将同时源方法运用到声波全波形反演来处理海洋拖揽数据.同时，Zhang等(2018)在声波同时源全波形反演中引入了一种全新的波场解耦方法.在该方法中，相敏检测(PSD)方法(Nihei and Li，2007)用来实现单频波场的完全解耦.同时，在他们的工作中，也给出了一些关键的实现步骤，比如采用随机的震源频率，可变的编码炮数等.基于这种PSD波场解耦的同时源编码策略，Tromp和Bachmann(2009)实现了同时源层析成像.为了进一步消除子波对反演的影响，Zhang等(2020b)将卷积型目标函数引入同时源反演中.同时，一种地震数据正则化的策略用来增强同时源反演算法的鲁棒性(Zhang et al.，2020a).

全波形反演就是同时使用波场的运动学和动力学特征.众所周知，如果初始模型不是很理想，多信息匹配很容易使得全波形反演陷入局部极小值，所以开展数据子集或者波场属性反演就显得十分必要(Sun and Schuster，1993；Fu et al.，2018；孟鸿鹰和刘贵忠，1999；马坚伟等，2000；董良国等，2015；梁展源等，2019).本文以同时源模拟与解耦的复波场为基础，拓展出实波场反演、虚波场反演及复波场反演策略，并通过数值结果来对比三种反演的优缺点.具体文章结构如下：在引言之后，回顾了无串扰的同时源反演方法；紧接着给出了实波场反演、虚波场反演以及复波场全波形反演的梯度表达式；接下来通过数值试验的方式说明复波场中的实部和虚部信息对波形反演的影响；最后一部分给出结论与建议.

1 方法原理

1.1 无串扰的同时源全波形反演原理

对于无串扰同时源的FWI，采用最小化位于检波点Xr的观测数据dobs(Xr,Ω,t)和合成数据u(Xr,Ω,t;m)的残差，其形式具体表示为：

(1)

其中，Ω表示角频率，x表示计算区域，并且Xr⊆x.给定一系列位于Xs的单频随机信号s(Xs,Ω,t)，则编码炮表示为：

(2)

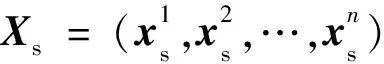
(3)

其中Xs⊆x，L[·]是声波正演模拟算子，相应的伴随方程表示为:

(4)

其中†表示伴随算子，并且：

(5)

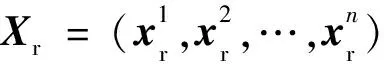
由于震源编码方法对应的梯度表达式和常规的梯度表达式一致，是正传波场与反传波场的特定形式的互相关.为了分析串扰噪声的影响，将梯度表达式简写为：

(6)

其中，梯度简写形式G(x,m)中的ψs(x,Ω)和ψr(x,Ω)分别表示正传波场与反传波场.在式(6)的第二个等式中，第一项表示每一炮数据的自相关运算，第二项表示当前炮与其他炮的互相关运算，即串扰噪声.由(6)式可知，只有从混叠的波场中解耦出所有炮的波场，然后只计算当前炮对应的正反传波场的自相关，才能从根本上消除串扰噪声.

有效地解耦混叠波场是解决编码噪声的关键，因此引入相敏检测方法来解决这个问题(Zhang et al.，2018；Tromp and Bachmann，2019).相敏检测方法的主要思想是利用两个与未知信号具有相同频率但彼此相位相差90°的参考信号(aref0°和aref90°)沿着时间积分来提取振幅为E相位为θ的目标信号as(t).为了简洁表示，取参考信号为sin(ωit)和其90°相移信号为cos(ωit).空间某一点的混叠波场可以表示为:

as(t)=E1cos(ω1t+θ1)+E2cos(ω2t+θ2)+…

+Enscos(ωnst+θns),

(7)

使|ωi-ωj|≥pΔω(i,j∈ns,p∈Z)，且Δω=2π/T.这里的T是地震记录的长度，p是最小的整数，pΔω表示编码信号之间的最小频率间隔.当定义最小的积分区间为Tp=T/p，对于任何整数q(p∈[1,p])倍的Tp区间qTp都可以作为合理的积分区间.通常，需要一定的时间等待波场达到稳态状况，所以q比p要小.在积分区间qTp上，参考信号sin(ωit)与混叠信号相乘并积分：

(8)

式(8)中，Ts表示波场达到稳态的时刻.

相似地，参考信号的90°相移信号cos(ωit)与混叠信号相乘并积分：

(9)

所以与参考信号相同频率的已知信号的振幅和相位可以解耦出来，其计算公式为：

(10)

式(8)和(9)积分主要利用了三角函数的正交性，只有与参考信号相同频率的信号的积分不为零，与其他频率的信号的积分为零，从而实现目标信号的提取.依次对空间中的所有点做上述积分计算，就可以求解出整个空间某一频率波场的振幅Ei和相位θi.同理，可以求取空间上其它不同频率的空间波场所对应的振幅和相位.则对应于每一个频率的空间正传复波场的共轭波场为：

u(x,ωi,t;m)=Eicos(θi)-iEisin(θi),

(11)

反传的复波场也具有类似的表达形式：

u′(x,ωi,t;m)=E′icos(θ′i)+iE′isin(θ′i).

(12)

然后通过梯度计算公式计算出目标函数对模型参数的梯度，其中速度模型的梯度计算式为：

(13)

式(13)中，Re表示取向量的实数部分.有了目标函数对应模型参数的梯度，可以通过优化算法求来迭代更新模型，具体的模型更新可以表示为:

mk+1=mk+tkΔmk+1,

(14)

式(14)中的k表示k次循环，tk表示选取的更新步长，Δmk+1表示利用收敛算法根据梯度信息构建的下降方向.本文采用共轭梯度算法来更新模型参数，其具体表达式为：

(15)

1.2 实波场、虚波场及复波场反演

无串扰噪声的同时源反演的前提条件是混叠波场的完全解耦，而实现混叠波场(正传波场和反传波场)的有效解耦方式是PSD方法.PSD方法只需要在波场外推的过程中沿着时间方向积分，如式(8)和(9)所示.波场信息的恢复如式(10)、(11)和(12)所示，从式子可以看到，PSD方法可以有效地得到空间波场的振幅和相位信息，并构建出显式的复波场，这为实波场、虚波场及复波场信息的反演奠定了基础.

基于式(11)、(12)和(13)的结果，可以自然地给出实波场、虚波场和复波场信息的反演梯度表达式.实波场反演是与波场相位的余弦有关，其梯度表达式为

(16)

其中greal表示实波场反演的梯度.虚波场反演是与波场相位的正弦有关，其梯度表达式为：

(17)

其中gimag表示虚波场反演的梯度.复波场的全波形反演方法，其梯度表达式为：

(18)

从式(18)可以看出，在全波形反演中，复波场的实部和虚部信息均参与了反演.

1.3 无串扰的同时源反演的算法流程

将PSD方法用到已知频率的混叠波场的提取中，可以实现无串扰的编码方法.通过提取当前炮的正传波场，以及对应的反传波场，通过对其进行特定形式的求取当前炮的梯度，以此方法求取编码炮内其他炮对应的梯度，叠加形成总的编码炮的梯度，进而求取所有编码炮对应的梯度.最后通过前面所述的共轭梯度算法更新模型并迭代反演.总结来说，基于PSD的声波同时源全波形反演步骤大致可分为以下6步：

(a)波动方程外推.选取一系列已知频率的单频信号并形成编码源，采用式(3)进行数值模拟.

(b)数据残差(虚源)计算.按照式(5)所示，分别从观测数据和合成数据中抽取某一炮的数据对应的单频地震记录，在观测系统的约束下求取该炮对应的数据残差，同理求取其他炮对应的数据残差并叠加形成编码炮的数据残差.

(c)伴随态方程外推.使用(b)中求取的虚源代入式(4)进行数值模拟.

(d)使用PSD方法进行波场解耦.从正传和反传的混叠波场中分别提取编码炮内的所有炮对应的波场响应，然后通过每一炮的正传波场的共轭波场与反传波场相关求得每一炮的梯度，通过叠加所有炮的梯度并形成总梯度.其中三种反演对应的梯度表达式如式(16)—(18)所示.

(e)通过共轭梯度算法更新模型.

(f)重复(a)—(e)直到达到设定的迭代次数或设定的目标函数的门槛值，终止反演过程并输出反演结果.

按照上述提到的6个步骤，设计了如算法1所示的具体程序实现框架.根据该算法，完成同时源的实波场、虚波场及复波场波形反演.

算法1 无串扰的同时源波形反演算法输入:观测数据和观测系统信息,初始速度以及反演参数输出:反演结果和目标函数值 do频带数循环 do迭代次数循环 do编码炮数迭代·同时源模拟和波场解耦·伴随源计算·伴随波场外推和波场解耦 enddo编码炮数迭代 计算(实波场、虚波场或复波场反演的)梯度并采用共轭梯度算法更新模型 enddo迭代次数循环 enddo频带数循环

2 数值试验

在数值试验部分中，使用Marmousi模型和Overthurust模型进行反演测试.程序设计为：CPU完成控制流和数据的输入输出，GPU负责核心的差分模拟计算.本文涉及的测试硬件为英特尔的i5-4460的CPU和GeForce RTX 3090的GPU.

2.1 Marmousi模型测试

首先采用Marmousi模型进行反演试算，模型如图1a所示.模型大小为6.63 km × 2.37 km，模型离散的空间步长为10 m.其中采用交错网格有限差分方法实现波动方程的离散，并在边界处引入吸收边界条件.有限差分的时间精度为2阶，空间差分精度为4阶.观测数据是采用15 Hz的雷克子波生成均匀分布的80炮数据，炮间距为80 m，每一炮均有663个检波点接收数据.地震记录的采样间隔为1 ms，模拟时间为8 s.反演所使用的初始模型如图1b所示，该初始模型是采用空间 2 km × 2 km对真实模型进行空间平均得到的.采用多尺度反演策略，总共划分5个频带进行反演，总共迭代100次.其中Marmousi模型对应的详细反演参数在表1中列出.

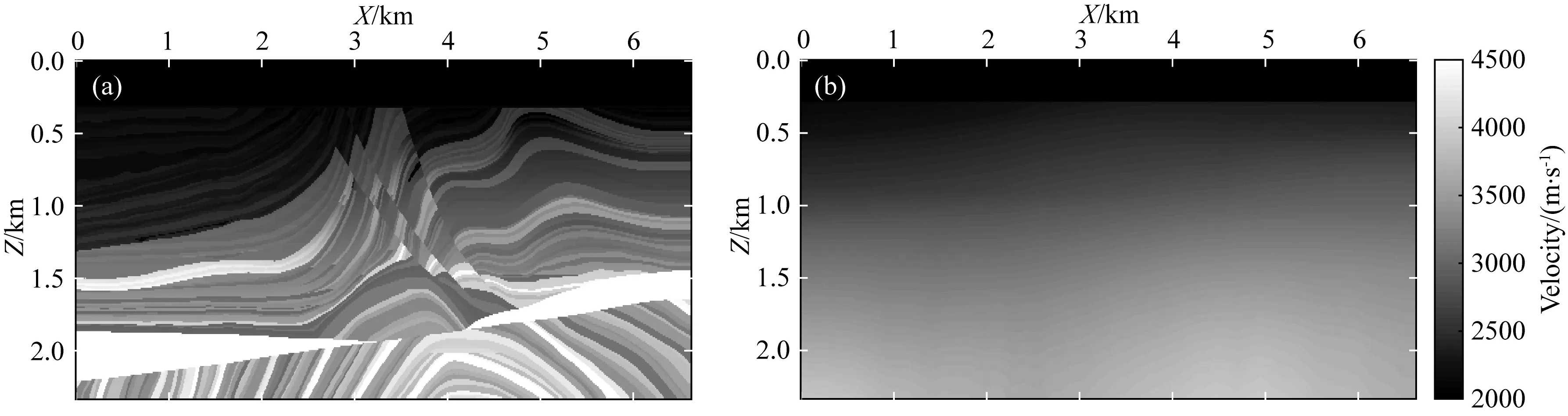
图1 (a)真实Marmousi模型；(b)初始模型

表1 Marmousi模型的反演参数

在反演之前，首先展示混叠波场的解耦过程.图2a是编码炮对应的最大时刻的混叠波场，图2b、c是解耦出的某一炮的振幅和相位信息；图2d、e是解耦出的另外一炮的振幅和相位信息.从图2可以看出，相敏检测方法可以在波场模拟中，通过积分的方式完全解耦出不同频率子波对应的波场信息，实现混叠波场的完全解耦.对于反传波场的波场解耦也是类似的过程.接下来比较三种反演策略计算的梯度.图3a—c分别展示了实波场反演、虚波场反演以及复波场反演在相同迭代次数的梯度.对比图3中的3个子图，可以看到实波场反演的梯度有着明显的振幅能量变化，虚波场反演的梯度更多是层的位置信息，整体能量均衡性比较好，复波场反演的梯度则同时具备实波场反演和虚波场反演的特征，梯度信息更加丰富，构造层次感比较强.

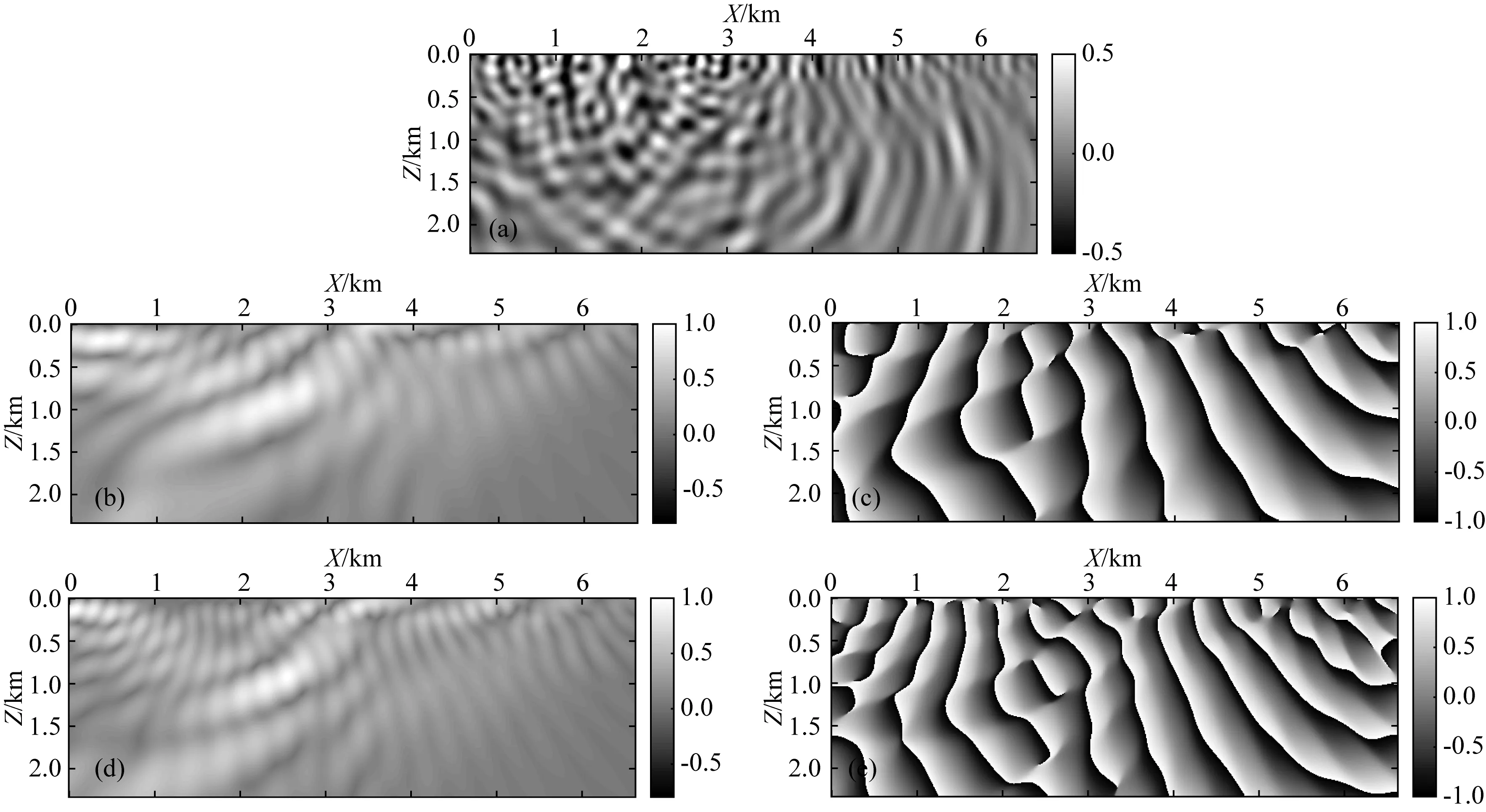
图2 (a)混叠波场，相敏检测解耦出的某一炮的(b)振幅信息和(c)相位信息，以及解耦出的另外一炮的(d)振幅信息和(e)相位信息

图3 Marmousi模型的梯度

在分析完梯度特征的基础上，开展反演试算.对于三种反演方法来说，除了选用的梯度计算不同之外，其余的反演参数均相同.此处展示了三种反演策略在第二个频带、第五个频带的反演结果，如图4所示.从最终的反演结果可以看到，三种方法均取得了比较好的反演结果，模型中的构造信息都得到了有效的恢复.通过仔细对比，相比于复波场全波形反演，无论是实波场反演还是虚波场反演，其反演结果的背景速度均有一定的模糊作用，分辨率有所降低.为了定量的评估反演结果的可靠性，本文采用式(19)来衡量计算结果的误差：

图4 Marmousi模型的反演结果

(19)

其中erra表示绝对误差，errr表示相对误差，nx和nz表示模型在二维空间的离散点数，|·|表示取绝对值运算.此处计算了反演结果的绝对误差，初始模型对应的绝对误差为263.68 m·s-1，实波场反演结果的绝对误差为203.82 m·s-1，虚波场反演结果的误差198.18 m·s-1，复波场反演的误差为193.90 m·s-1.对比最终反演结果的绝对误差，可以发现复波场反演的精度最高，其次是虚波场反演.为了更清楚地展示反演结果，抽取位于x=2.2 km和x=4.2 km的反演结果并分别展示在图5a、b中.从反演剖面上可以看出，复波场反演在某些局部位置可以得到更加准确的速度值.

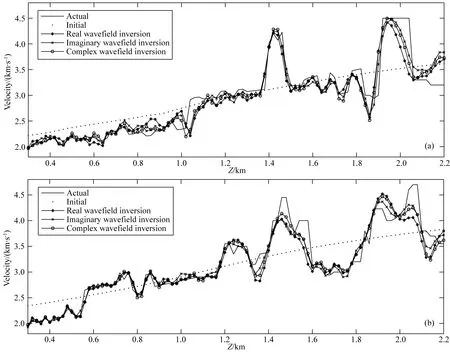
图5 Marnousi模型位于(a)x=2.2 km和(b)x=4.2 km处的反演剖面对比

图6a、b分别展示了三种方法对应的目标函数值及模型误差值随着迭代次数变化的曲线，此处模型误差值是通过式(19)中的相对误差计算得到的.从图6中可以看出，随着迭代次数的增加，目标函数和模型的相对误差都呈现明显的下降趋势.就目标函数的下降曲线而言，尽管虚波场反演的目标函数下降曲线与复波场反演的曲线吻合度较高一些，但三种方法的差异不大；从模型参数的下降曲线可以看出，反演的初始阶段，虚波场反演与复波场反演的误差有着很高的一致性，且优于实波场反演方法；随着迭代次数的进一步增加，相位反演的模型收敛性变差，这说明复波场反演中的实波场信息在高波数反演中贡献突出.

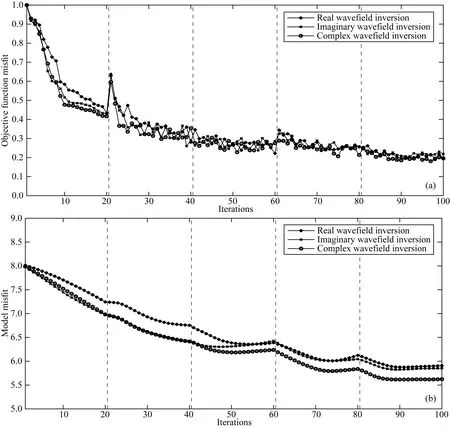
图6 目标函数值(a)和模型误差值(b)随着迭代次数变化曲线

2.2 Overthrust模型测试

接下来，在Overthrust模型上进行反演测试.模型大小170×800，网格间距10 m.采用主频为15 Hz的雷克子波生成100炮数据，数据的时间采样点为1 ms，地震记录长8 s.模型的真实速度如图7a所示，反演所使用的初始模型如图7b所示.初始速度模型是一个随着深度递增的线性速度模型.相比于Marmousi模型反演所用的初始模型，此处使用的初始模型比较粗糙，因此会使得反演目标函数的非线性增强，所以依旧使用多尺度反演策略来降低反演的多解性.反演中使用了5个反演尺度，每个频带的频率范围及编码炮个数不相同，具体的反演参数如表2所示.

图7 (a)真实Overthrust模型；(b)初始模型

表2 Overthrust模型的反演参数

依旧设计了三种反演方法试算，在这三种反演算法中除了梯度计算不同外，其余的反演参数均相同.最终的反演结果如图8a—c所示，其中图8a—c分别为实波场反演、虚波场反演以及复波场反演结果.从反演结果可以看到，在初始模型比较差的情况下，实波场反演不能得到有效的模型参数，尤其是在黑框所标记的逆冲断层处成像效果很差；对于虚波场反演而言，即使是初始速度较差的情况下，依旧能取得比较好的反演结果，并且其成像分辨率基本上与复波场反演的分辨率相当，这就说明虚波场反演对速度模型的敏感度较低.由于全波形反演是实波场和虚波场信息的综合使用，这说明全波形反演的低波数成分主要由虚波场信息来恢复，从而避免陷入局部极值的问题；随着模型的低波数成分被有效地恢复，全波形反演可以综合使用实波场和虚波场信息实现高分辨率的反演结果.于是，本文开展了一种组合的反演试算，即在低波数反演中，采用虚波场反演，在高波数反演中，使用复波场反演，这样可以降低实波场反演对低波数的依赖性.组合反演的最终结果如图8d所示，从反演结果上可以看到，相比于虚波场反演，反演精度有了明显的提升，并达到了与复波场反演接近的精度.为了更好地对比编码方法的反演结果，图8e展示了常规序列源的反演结果.对比发现，采用序列源带宽子波反演方法，反演结果在层内具有更好的光滑性，但是层界面不是很清晰.相似地，初始结果和五种反演结果的绝对误差也被计算：初始模型对应的绝对误差为439.80 m·s-1，实波场反演结果的绝对误差为349.11 m·s-1，虚波场反演结果的误差216.80 m·s-1，复波场反演的误差为166.45 m·s-1，组合反演结果的误差为191.28 m·s-1，以及常规序列源反演的误差为207.10 m·s-1.对比最终反演结果的绝对误差，可以发现虚波场反演的精度可以通过组合反演策略得到提升；同时，也可以从图9中的局部反演结果对比得到相同的结论.

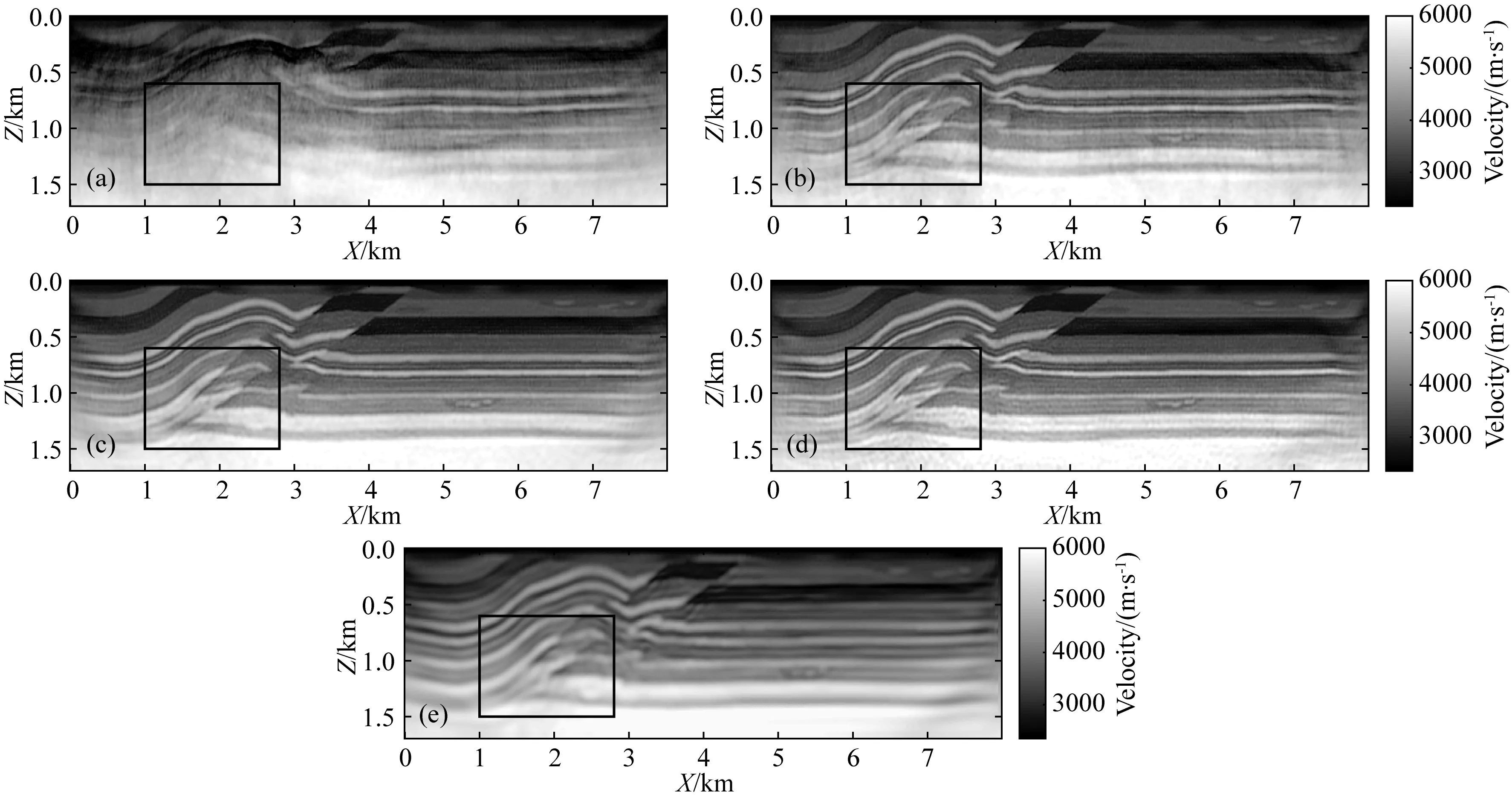
图8 Overthrust模型的反演结果

图9 Overthrust模型的反演结果局部显示

相似地，五种反演方法对应的目标函数值及模型误差值随着迭代次数的变化曲线被绘制在图10中.在图10a，可以看到在五个反演尺度中，目标函数均呈现出比较好的下降趋势；除了常规序列源反演包含着丰富的数据量，所以目标函数的残差整体比编码方法的残差要大；在编码方法中，相比于其他几种反演方法，实波场反演的目标函数在低频下降缓慢，同时对比图10b，实波场反演的模型不收敛，这说明实波场反演已经陷入局部极值；虽然复波场反演在低频有着最大的下降率，但是随着迭代次数的增加，其目标函数的下降曲线逐渐与虚波场反演相一致；对于组合的反演方案，在开始阶段与虚波场反演吻合度很高，随着迭代次数的增加，其目标函数值逐渐低于虚波场反演，直至最后的频带，组合反演的目标函数值是四种反演算法中最低的，这说明这种策略可以降低目标函数的复杂度，使得目标函数下降的更多.

从模型下降曲线(图10b)可以看出，实波场反演的模型收敛性最差，虚波场反演、组合反演，复波场反演，和序列源反演均呈现出比较好的模型收敛性，且在模型的收敛性方面复波场反演优于组合反演，组合反演优于虚波场反演和序列源反演.值得注意的是，第四个频带处，复波场反演出现了小幅度的模型误差增加，这充分说明了复波场反演的高度非线性性.

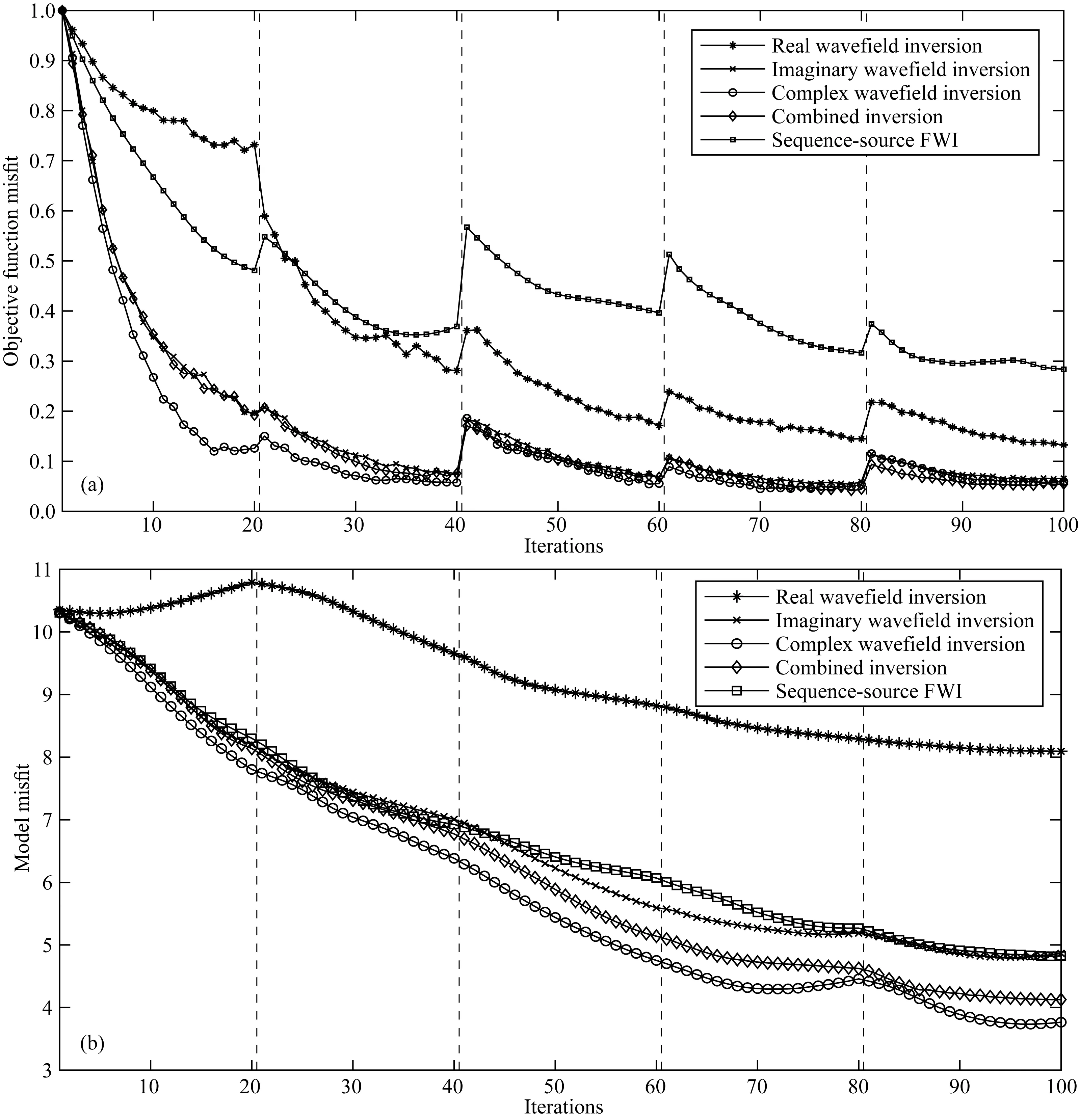
图10 目标函数值(a)和模型误差值(b)随着迭代次数变化曲线

3 结论与讨论

(1)在地震建模中，全波形反演具有高精度建模的潜在优势.主要有两方面挑战限制了该方法的大规模应用.第一个方面是计算效率的问题，本文引入的无串扰的同时源反演方法，可以有效地提高计算效率且不影响成像质量；第二个就是该反演方法是高度非线性的，因此对初始模型有着很强的依赖性.本文从复波场信息解耦的角度出发，给出了实波场、虚波场以及复波场反演的方法，在反演中分别或者共同使用复波场的实部和虚部信息，这对复杂介质速度建模有着重要的意义.

(2)从实波场反演、虚波场反演、到复波场反演的试算可以看出，当初始速度比较准确时，三种方法都能得到比较好的反演结果；当初始模型准确性较低时，实波场反演很快就陷入局部极值；而虚波场反演依旧可以得到比较好的反演结果；这说明实波场反演对初始模型的依赖性较强，综合使用实波场和虚波场反演的全波形反演，在低频反演阶段主要是虚波场反演的作用保证反演不陷入局部极值.因此，一种组合的反演策略，低频采用虚波场反演，高频采用复波场反演可以在复杂模型建模中有一定的应用潜力.

(3)本文目前只开展了基于声波方程的复波场实部和虚部反演研究.由于弹性波场更加复杂，目标函数的局部极值更多，下一步工作可以考虑在弹性波反演中做进一步研究，来增强弹性波动方程波形反演建模能力.