基于频率-结构双重加权阈值的地震数据插值
陈思远,曹思远*,孙耀光,江雨濛,高君
1 中国石油大学(北京),北京 102249 2 中国石化石油勘探开发研究院,北京 100083
0 引言
地震采集与处理过程中,受空采区和坏道的影响,会出现地震道的缺失,需进行数据补全,为后续地震数据的反褶积、偏移以及储层反演等工作提供优质数据体.最早使用的插值方法为FX域(Spitz, 1991)和F-XY域(Wang, 2002)的插值方法;考虑相邻地震道的相似性,出现以差分算子为约束的插值方法(Liu et al., 2015; Zu et al., 2016),并认为缺失地震数据左右两侧的平均为缺失处的数据,由于叠前数据倾角较大,该方法效果不尽理想;由此,基于倾角约束(Hedefa et al., 2010)的插值方法便应运而生,包括基于倾角约束的中值滤波方法等(Huo et al., 2017).另一方面,在波动方程领域,有部分学者以速度为约束,以波动方程为媒介进行插值等(Swindeman and Fomel, 2015).
近年,随着压缩感知恢复算法的发展,逐渐提出基于稀疏约束的插值算法(刘洋等,2018;孙苗苗等,2019),其假设无缺失数据经过某种变换后,在变换域中呈稀疏态,而缺失地震数据在变换域内非稀疏,相比于无缺失数据,缺失地震数据变换域内的幅值较弱,可使用阈值压制这些非稀疏能量以完成缺失数据的补全.目前,可用变换包括Fourier变换(Gülünay, 2003;王锦妍等,2020)、FK变换(Wang and Lu, 2017)、小波变换(Guo et al., 2015)、Curvelet变换(Herrmann and Hennenfent, 2008;Yang et al., 2012)、Shearlet变换(Liu et al., 2018)、Radon变换(Yu et al., 2007)及Seislet变换(Gan et al., 2015;邓盾等,2019)等.除此之外,低秩约束作为特殊的稀疏约束也被应用到地震数据的插值中(Chen et al., 2019; Lari et al., 2019; Pan et al., 2017).
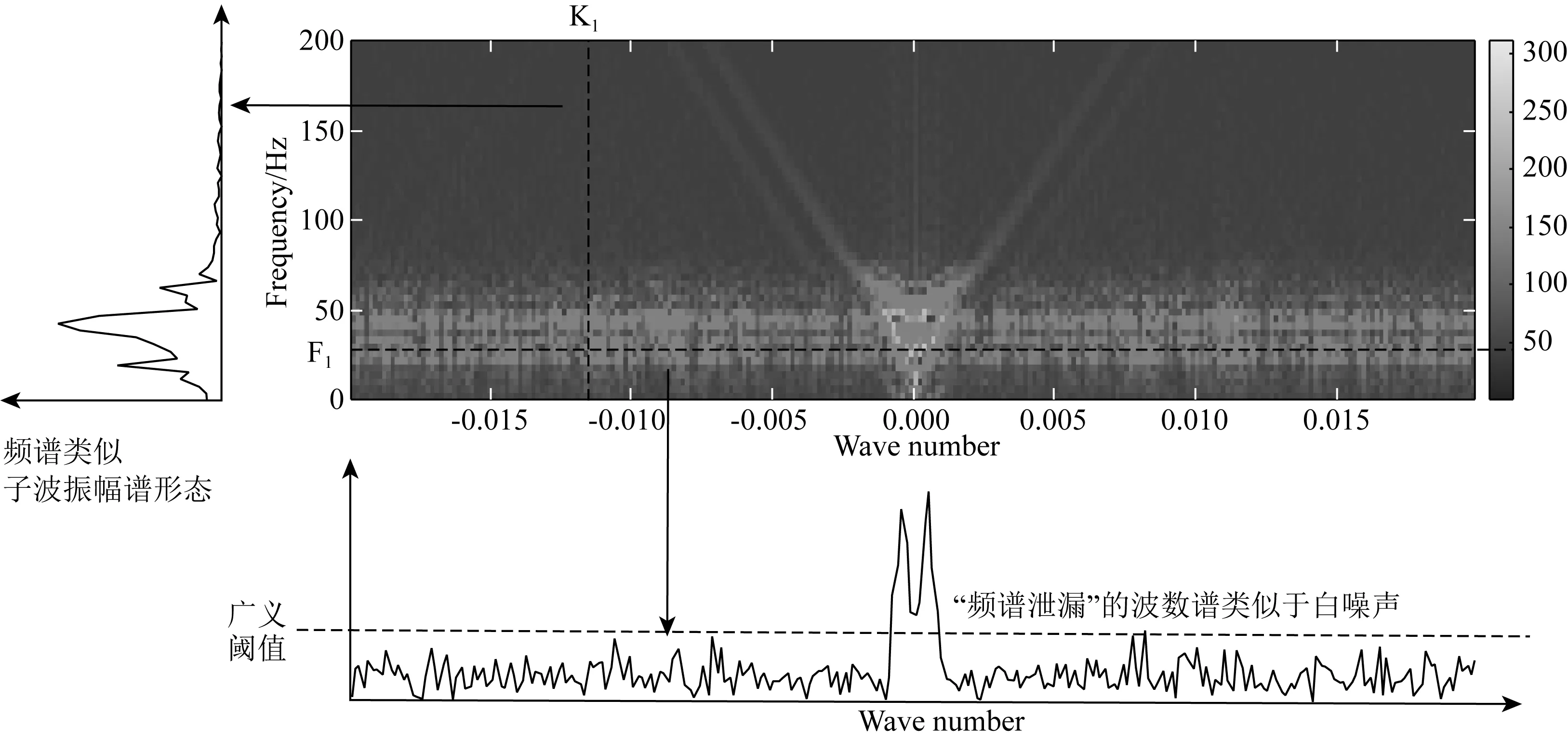
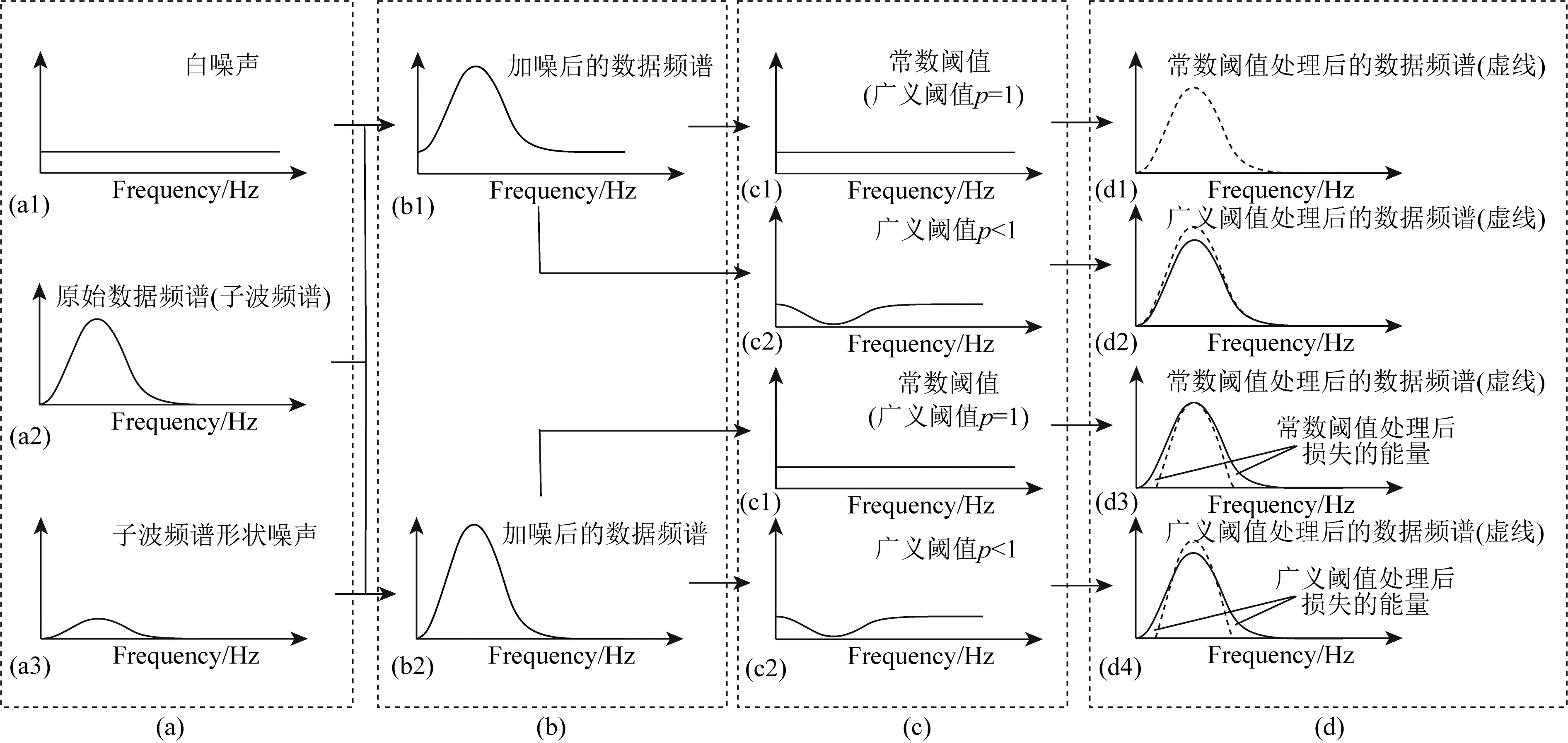
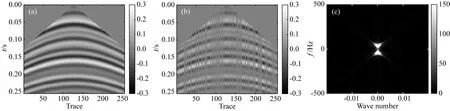
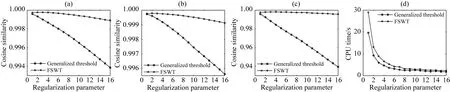
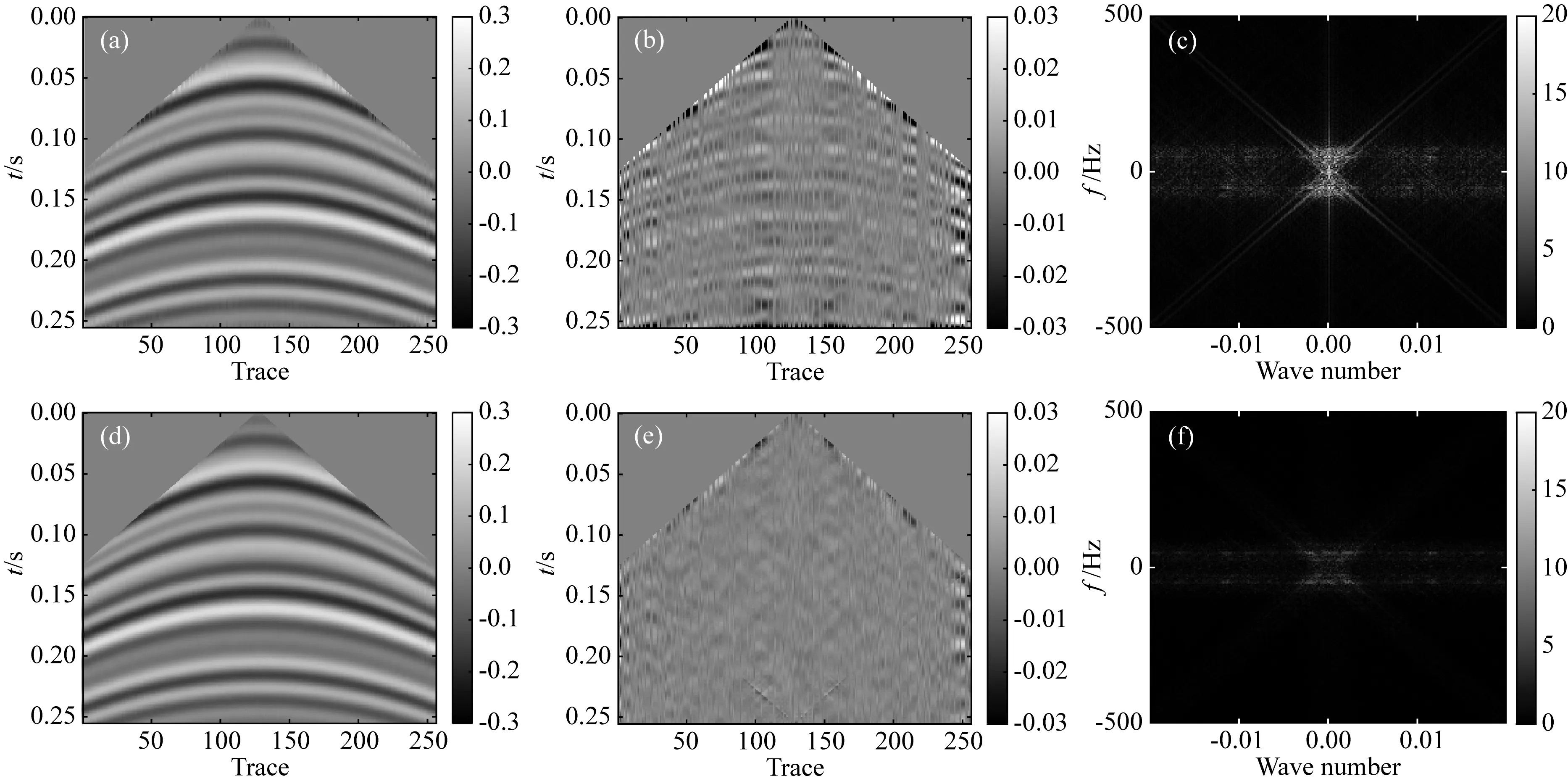
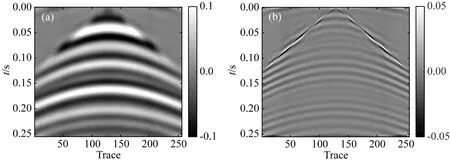
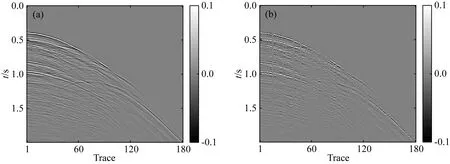
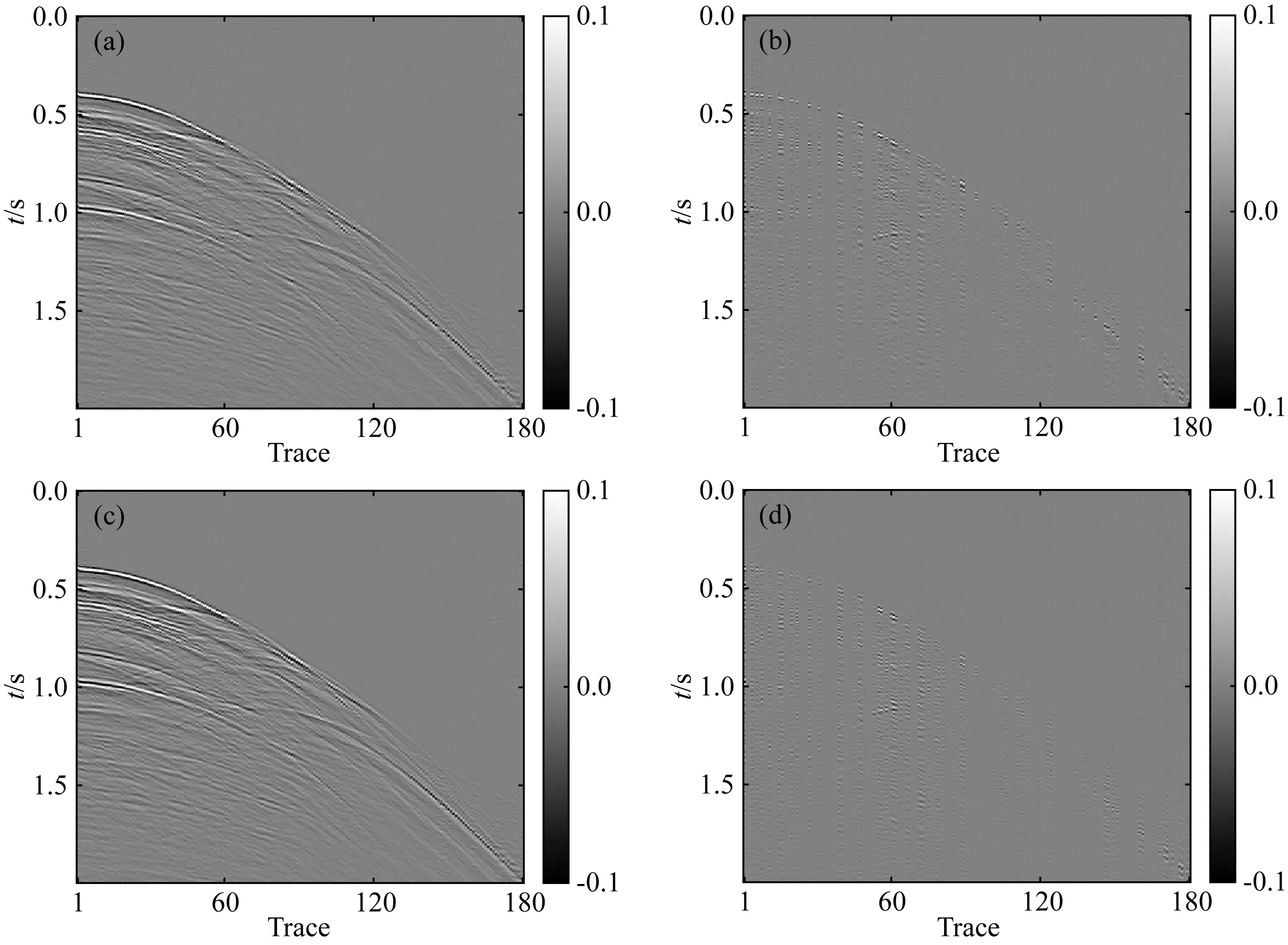
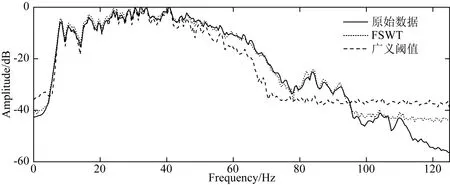
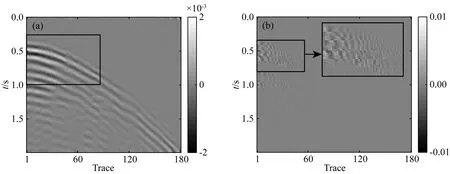
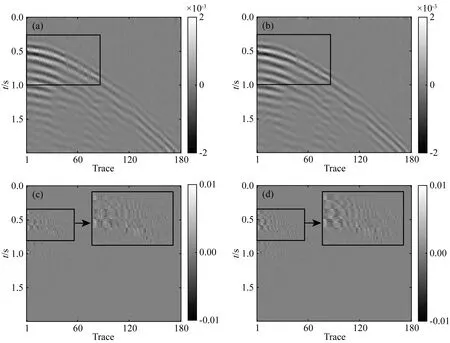
在稀疏约束目标上,L0范数是标准的稀疏约束,该范数的求解是NP难问题(Natarajan, 1995),可使用L0范数的最佳凸近似L1范数代替L0范数求解(Chen et al., 1998),当s表示稀疏度,且满足δ2s 基于稀疏约束的地震数据插值方向,深入讨论稀疏变换域结构特性的研究论文较少,通常假设其整体的稀疏性,未考虑信号及变换域的特征,导致变换域中的弱能量被广义阈值压制.本文从频率-波数(FK)域的结构入手,探究沿频率方向和沿波数方向有效能量及缺失数据分布特征,以减少变换域中的弱有效能量损失.在现有的研究基础上开展如下工作:(1)以FK变换为例,使用图示描述基于Lp范数的广义阈值(下称广义阈值)所造成的被插值数据的高低频缺失现象,探究在FK变换域中缺失数据沿频率方向的形态,构造频率加权阈值(FWT);(2)针对FK变换域的波数方向的聚集性特征,构造结构加权阈值(SWT)以提高稀疏约束能力;(3)模型测试部分,合成简单模型分别测试“广义阈值”、“频率加权阈值(FWT)”、“结构加权阈值(SWT)”、“频率-结构双重加权阈值(FSWT)”在插值中的作用,以佐证理论部分的正确性;最后,以实际缺失地震数据测试本文所提出的频率-结构双重加权阈值在缺失数据高低频恢复上的有效性. 需要指出,除FK变换域可作为稀疏变换域之外,Curvelet变换、小波变换、Shearlet变换等均带有频率的分解,以满足不同频率下数据的稀疏表达;因为地震数据各频率成分比重不同,所以本研究以FK变换作为稀疏变换旨在证明“频率-结构双重加权阈值”相比于“广义阈值”在数据高低频恢复中的有效性,其他的带有频率分解的类似稀疏变换均可依照该思想构造相应的加权阈值. 时间采样点为n的m道地震数据插值可以使用正演方程描述为: Y=LX, (1) 其中,Y∈mn×1表示观测数据,即含缺失地震道的数据,L定义为式(2)所示的正演算子,其中,I和0分别表示单位矩阵和零矩阵,可从完整数据X中采样得到观测数据.式(2)为: (2) 采样矩阵L是秩亏矩阵,待求的完整数据X具有无穷个解,基于压缩感知理论,可施加不同的正则化约束保证待求X的解唯一,并尽可能获得最接近真实数据的解.常用的正则化约束包括Tikhonov约束(Fleming, 1990)(L2范数约束),稀疏约束(L0范数约束)等,可通过压缩感知理论建立如下约束方程: (3) 其中,B表示某种变换,完整数据X在变换B的作用下可以符合Lq-Norm(0≤q<2)的约束,整形正则化理论表明,可以通过约束待求解数据变换域中的形态以获得最接近真实数据的解;传统方法假设完整数据在FK域中稀疏,而缺失后的数据非稀疏,通过整形正则化的方法求解该模型得到最接近真实数据的解.将式(3)写为如式(4)所示的无约束优化问题,并使用稀疏约束作为正则化项: (4) 式中,λ定义为正则化算子,由于L0-norm的求解是NP-hard问题,所使用的求解算法是匹配追踪等(Mallat and Zhang, 1993),该类算法需预先给定稀疏度,而完整数据FK域的数据稀疏度无法确定,故匹配追踪类算法不适用方程(4)的求解;考虑以Lp-norm近似L0-norm,(0 (5) 式(5)可以通过整形正则化的方法在多项式时间内有效求解(Ge et al., 2011),给出迭代步长α,对应于式(5)的迭代方程为: X(k+1)=B-1TλB[X(k)-αLT(LX(k)-Y)], (6) 式中,Tλ为式(7)定义的广义软阈值处理算子: (7) 1.2.1 含缺失道的地震数据在FK域的结构特性 当B为FK变换时,式(5)被称为FK域的插值反演方程.地震数据因为其频带宽度有限,同相轴曲率较小,在FK域中呈聚集性分布;高波数、高频率位置因地震数据构造的特殊性,也会出现部分弱能量.而由于地震数据不规则缺失现象,缺失地震道的位置产生截断,如图1所示,造成沿波数方向的“频谱泄漏”,随缺失道的增加,“频谱泄漏”的能量也随之增加,缺失地震道的能量将类似于“白噪声”均匀分布在沿波数方向上(图1中F1处的虚线),可使用广义阈值压制(图1下方虚线);另外,在沿频率方向上,缺失数据并未造成频谱泄漏(图1中K1处的虚线),故而广义阈值应单独作用于沿波数方向,不应作用于沿频率方向上. 图1 缺失地震数据FK谱形态示意图 图2模拟广义阈值对白噪声(频谱为白谱)和类子波频谱形态的噪声(频谱形态类似为子波频谱的形态)的压制效果及所带来的问题;当噪声为白噪声时(图2a1),合适的广义阈值可以有效的压制噪声的干扰(图2d1和图2d2),且可以保留高低频能量;而当噪声为子波频谱形态时(图2a3),广义阈值也压制了噪声的干扰,但是损失了高频和低频的能量(图2d3和图2d4). 图2 不同频谱形态的噪声与常数阈值的测试示意图 1.2.2 基于FK域的频率-结构双重加权阈值的构造 在地震数据处理中,低频和高频的能量是提高分辨率和储层反演所需要的,广义阈值在处理类子波频谱形态的噪声中损伤了能量较弱的低频及高频信号;对于类子波频谱形态的噪声,考虑使用类子波频谱形态的阈值进行处理,即能量弱的部分减小阈值,联系上文缺失地震数据FK变换,沿波数方向的“频谱泄漏”相当于在每个波数上均增加了类子波频谱形态的噪声,在使用广义阈值进行处理时,低频和高频所对应频谱能量较弱的位置,广义阈值会压制弱能量,将造成缺失数据高低频的损失,故而在基于FK域的地震数据插值中需要构造呈类子波频谱形态的沿频率方向的阈值加权算子. 缺失数据造成的“频谱泄漏”沿波数方向呈均匀随机分布,可使用广义阈值进行压制,当缺失数目较多时,“频谱泄漏”的能量逐渐逼近甚至超过有效信号的能量,这需要沿波数方向构造一个随FK谱结构变化的加权算子,进行沿波数方向的结构加权;基于频率-结构的双重阈值加权算子的构造方式如下. 记观测数据Y经过沿时间方向的Fourier变换得到的数据为Yf,x,式(1)可写为: Yf,x=LXf,x, (8) 式中,Xf,x表示完成数据X经过沿时间方向的Fourier变换得到的数据,对于数据的每个频率切片fi,(i=1,2,…,m),式(8)可写为: Yfi,x=L0Xfi,x,i=1,2,…,m, (9) 其中,L0=diag{1,1,…,0,…,1}n×n仍为采样算子,若Xfi,x在变换域B中为稀疏态,且Yfi,x在变换域B中为非稀疏,则可通过式(10)所示的压缩感知重建方法得到每个频率切片对应的完整的数据Xfi,x,遍历所有频率切片即完成缺失数据的恢复: (10) 根据式(3)—(6),约束方程(10)也可以使用整形正则化方法求解,即: (11) (12) 另外,考虑变换域的稀疏性,引入反加权算子hfi,x增强完整数据的每个频率切片的稀疏约束能力,则式(10)改写为: (13) 将频率-结构双重加权阈值代入式(7)中,将广义软阈值修改为式(14),结合整形正则化的迭代式(6),可进行基于频率-结构双重加权阈值的缺失地震数据补全: (14) 本部分首先使用128×128的合成模型,分别测试广义阈值,频率加权阈值(FWT),结构加权阈值(SWT)和频率-结构双重加权阈值(FSWT)各自的作用;如图3a所示,该模型从左到右Ricker子波主频由15 Hz递增到95 Hz;加入高斯白噪后信噪比为24.68 dB. 应用上述四种阈值进行插值,单次插值误差剖面见图3b—e,因为SWT作为结构加权阈值,是全频带的保幅阈值,误差变化不明显;同时,FWT重点倾向于弱频率能量的保护,在此模型中对应于能量较弱的高频,故而在全频带的误差剖面上,四种阈值所产生的误差形态接近.经计算,四种阈值插值结果与原剖面的余弦相似度分别为:广义阈值:99.27%,FWT:99.44%,SWT:99.41%,FSWT:99.56%. 为了直观的体现频率加权阈值对数据高频补全的重要性,应用时频分析工具对四种阈值的插值结果及无缺失数据进行频率分解,分解得到的高频剖面见图4.广义阈值和SWT的插值结果的高频剖面表明基于广义阈值的插值难以补全高频成分(图4b),而本文提出的FWT和FSWT的插值结果分频剖面同相轴连续性较好(图4c和图4e),证明FWT和FSWT在缺失数据高频恢复上的有效性. 因为模型的主频是道号的函数,本部分重复试验100次随机缺失数据插值,绘制四种阈值插值结果逐道与原剖面(图3a)的相似度(图5),当频率处于中低频时(<35 Hz),相似性FSWT>SWT>FWT=广义阈值;在证明SWT的保幅效果优异的同时,也说明FWT在能量较强的中低频部分保幅效果较弱;在高频部分(>70 Hz),相似性FSWT>FWT>SWT>广义阈值,说明FWT在数据高频部分保幅性优异;而SWT在整个频带的相似性排名均优于广义阈值,证明SWT在全频带具有一定保幅作用. 图3 原始数据及插值误差 图4 分频剖面(高频) 图5 四种阈值插值结果与无缺失数据的余弦相似度 继续合成256道,含256个采样点的叠前地震数据;如图6所示为原始数据、缺失50%地震道的地震数据和缺失地震数据的FK谱;添加随机噪声后,信噪比为32 dB.本部分将测试广义阈值和频率-结构双重加权阈值(FSWT)对图6所示复杂模型的适用性.测试环境为Inter i7-9750H处理器,16 GB内存,软件环境为Matlab2020a. 图6 合成模型 对于插值反演方程,正则化参数对插值结果影响相对较大.分别选择不同的正则化参数进行插值测试,记录插值后与原始数据的余弦相似度、插值后与原始数据低频剖面以及高频剖面的余弦相似度和计算时间的曲线如图7所示:当正则化参数逐渐变小时,任何频带范围内,基于广义阈值的插值方法和基于FSWT的插值方法所计算的余弦相似度趋于相同(图7a—c),但是计算量呈指数型增加(图7d);而当正则化参数逐渐变大时,基于广义阈值的插值方法的相似度快速下降,而基于FSWT的插值方法余弦相似度变化不明显(图7a—c),同时,计算时间趋于稳定(图7d),综合考虑计算成本,如图8所示取正则化参数等于8时的插值结果进行分析. 图7 正则化参数对插值性能的影响测试 基于广义阈值的插值方法的误差剖面上(图8b)可见大量同相轴,且误差剖面的FK谱上有较多聚集性能量(图8c),插值结果较差;相比于前者,基于FSWT的插值方法的误差剖面无明显可见同相轴,FK域中的聚集能量也较少(图8d). 将图6a所示的无缺失数据进行分频,取低频(主频约18 Hz)及高频(主频约66 Hz)的剖面如图9所示;同时将图8a和图8d所示的插值结果也进行分频,绘制高低频插值结果及误差剖面如图10所示;无论是低频或者高频部分,基于广义阈值的插值方法的分频误差剖面上(图10b和图10d)均可见同相轴,且缺失数据未成功恢复;基于FSWT的插值方法低频及高频误差均较小,无缺失地震道现象出现(图10f和图10h). 图8 基于广义阈值和FSWT的插值结果 图9 无缺失数据分频剖面 实际数据测试部分,选择M地区实际数据进行插值处理,该数据含有180道,采样率为4 ms,本文置零约35%的地震道以测试广义阈值和FSWT的插值效果.如图所示,图11a和图11b分别为原始数据和缺失地震道的数据;图12为使用广义阈值和FSWT的插值结果与误差,从插值剖面上无法看出两种阈值的区别(图12a和图12c),在相应的误差剖面上(图12b和图12d)FSWT的插值误差小于使用广义阈值的插值误差;同时,本文计算使用两种阈值插值后剖面缺失位置所占无缺失数据缺失位置能量的比重分别为:广义阈值:75.7%;频率-结构双重加权阈值:89.9%,这证明本文所提出的FSWT在全频带上的保幅性优越于传统广义阈值. 图11 实际单炮数据和缺失35%地震道的数据 图12 基于广义阈值和FSWT的插值剖面和误差 图11a、图12a和图12c的缺失地震数据位置的频谱如图13所示,基于FSWT插值的结果较好的拟合原始数据的频谱,而基于广义阈值的插值结果在低频和高频与原始数据频谱的相似度均较弱;为了得到更准确的测试结果,应用时频分析工具对原始数据(图11a)以及插值后的数据图12a和图12c进行频率分解,低频(主频约为9 Hz)及高频剖面(主频约为90 Hz)如图14和图15所示,相比于图14所示的原始数据分频结果,本文提出的FSWT无论是低频(图15b)或者高频(图15d)的插值效果均优异于广义阈值的插值效果(图15a和图15c). 图13 实际单炮数据和插值后数据的频谱 图14 无缺失数据的高低频剖面 图15 基于广义阈值和FSWT插值后的高低频剖面 针对基于传统广义阈值插值所造成高低频难以补全的问题,本文考虑FK域中缺失数据频率方向的非稀疏,构造类子波形状的频率加权算子,同时注意到波数域有效能量聚集性,联合频率加权算子,提出频率-结构双重加权算子进行缺失地震数据的补全,一定程度上解决了传统广义阈值对于缺失位置高低频难以恢复的问题,保证后续处理环节的进行.算法在适用性方面仍有较大研究空间: (1)基于频率-结构双重加权阈值主要作用在于恢复缺失位置处、能量较弱高低频信息,由于中频段(主频附近)的FSWT与广义阈值的大小、形态均接近,所以在该频段内算法改善效果不佳. (2)频率域的非离散现象不仅在FK域中出现,包括Curvelet域、Shearlet域等涉及频率的变换域均有此现象,也可通过构造频率加权算子提高这些变换域的插值精度. (3)对于三维数据,可采用频率-波数-波数(FKK)或者3D-Curvelet作为稀疏变换域,按本文方法可构造三维加权阈值进行高低频信息的有效恢复. (4)本文仅在FK域进行加权算子的可行性研究,由于地质构造通常较复杂,可能含有绕射波等大倾角构造,由于变换域限制,大倾角同相轴补全效果不佳,可使用其他稀疏变换域(Curvelet变换)联合频率-结构双重加权阈值对这部分弱能量进行有效恢复.1 理论
1.1 基于稀疏反演的地震数据插值理论
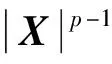
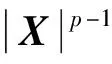
1.2 频率-结构双重加权阈值的构造
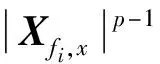
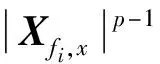
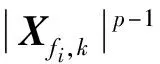
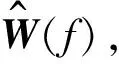
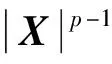
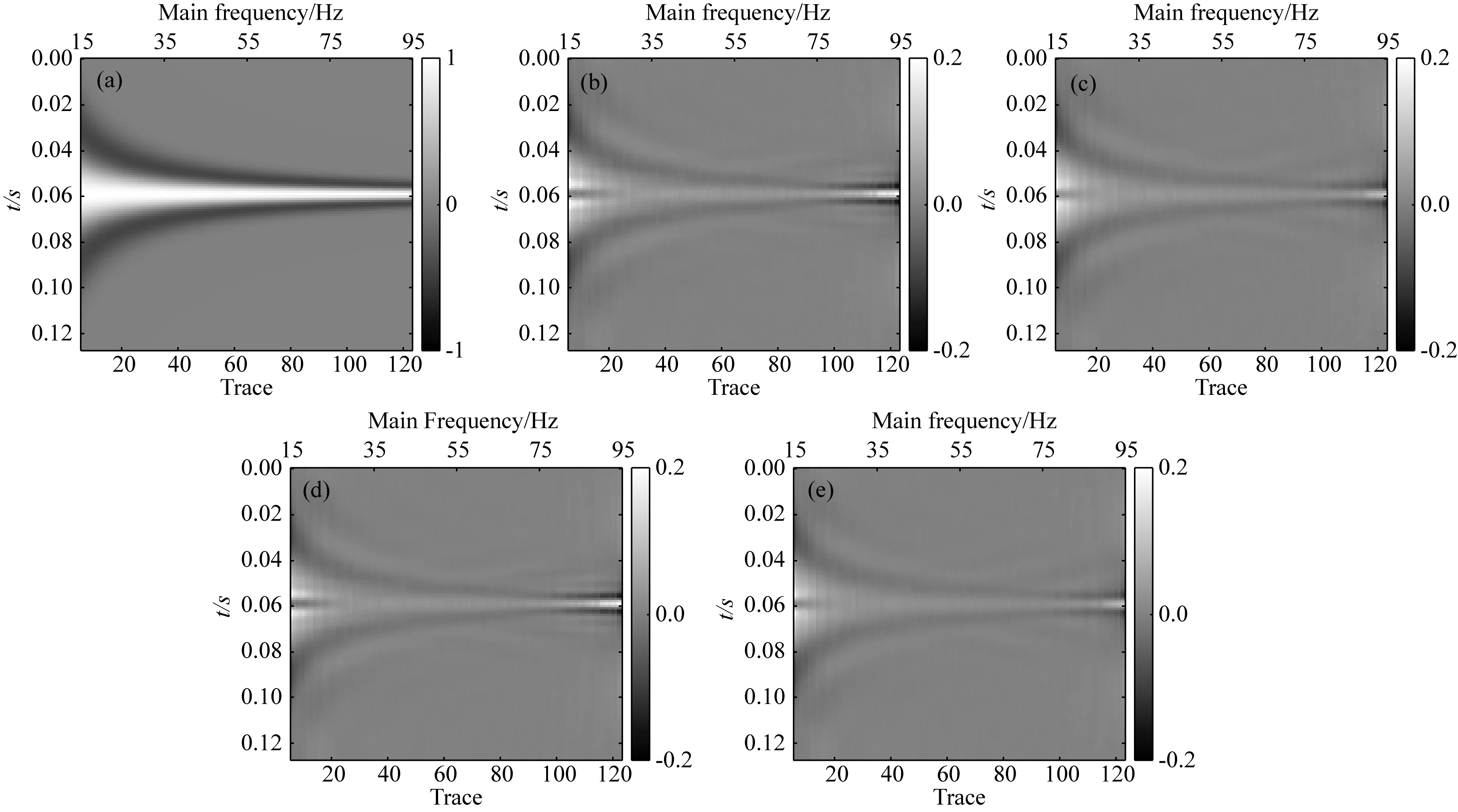
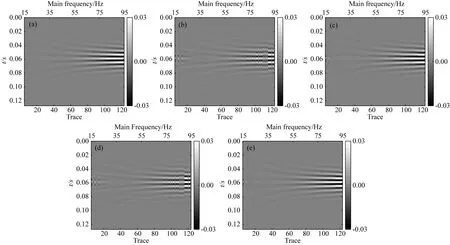
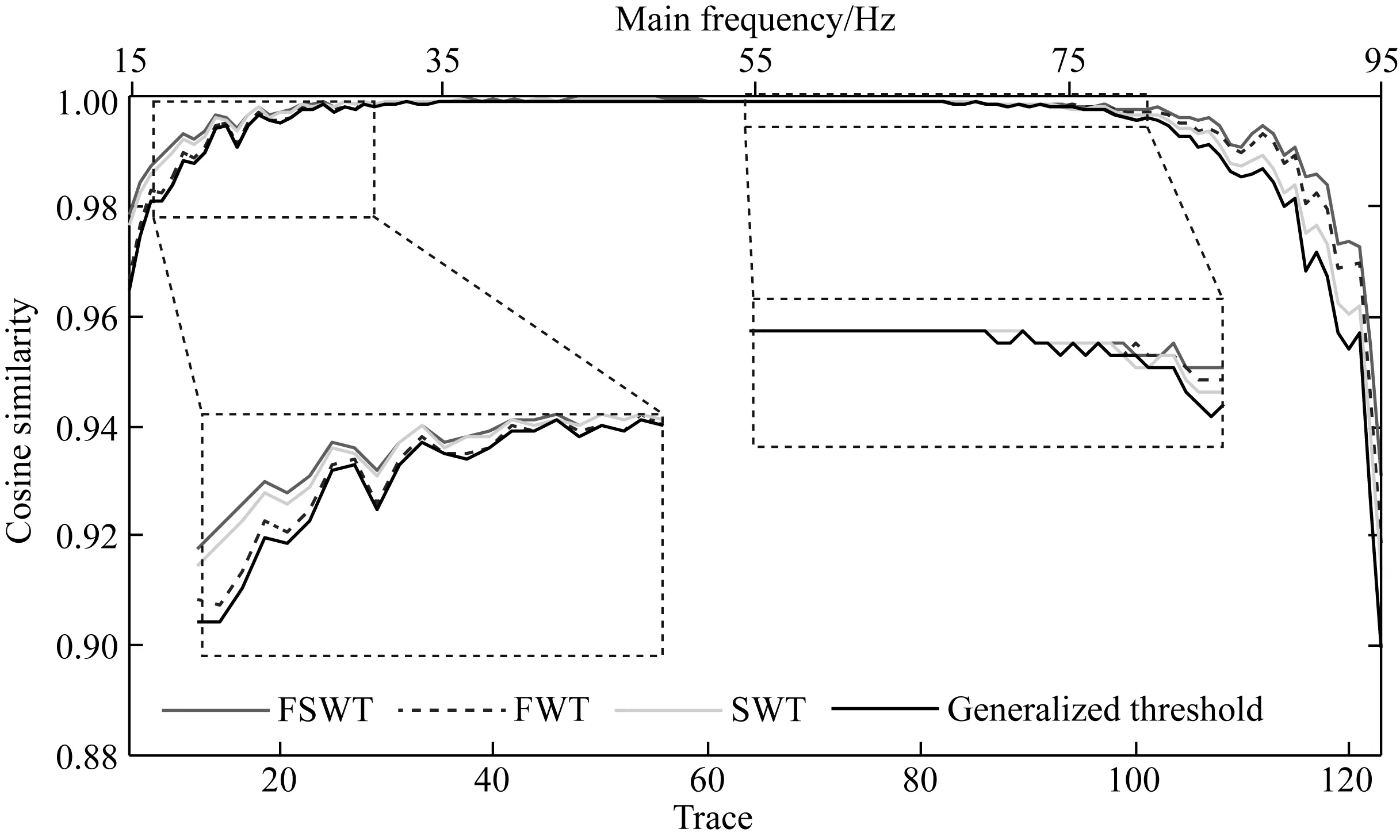
2 模型测试
3 实际数据测试
4 结论

